WOO logo

Recomendações do Mago

Dados - Dados e Rolagem

Gostaria de saber como alterar os dados no jogo de craps para que saiam sempre 7 ou 11. Você pode me ajudar? Obrigado.

d de Monterey, California

Altere então o dado de forma que um tenha um seis em cada face, e o outro tenha apenas uns e cincos.
Você acredita que o "pensamento positivo" dos jogadores pode afetar o resultado de um jogo? Observe que não estou preocupado com a magnitude do efeito, apenas com sua opinião filosófica. Além disso, você acha que a maneira como um jogador lança os dados no craps pode causar um viés (positivo ou negativo) no resultado? Como sempre, seu site é incrível.

Ted F. de Perth Amboy, New Jersey

Obrigado pelas palavras gentis. Não, não acho que ter esperança ajude no cassino, considerando todas as outras coisas iguais.

A questão da influência dos dados é um tema muito debatido. Pessoalmente, sou bastante cético. Ao revisar esta resposta em 2013, ainda não encontrei nenhuma evidência convincente de que alguém possa influenciá-los o suficiente para obter vantagem.
Gostaria de saber sua opinião sobre alterar a tabela de frequência no jogo de dados (craps) pré-definindo os dados.

Thom de San Francisco, USA

Sou muito cético quanto a isso. Analiso alguns dos experimentos sobre o assunto no meu apêndice 3 sobre craps .
Recentemente, aprendi algumas informações sobre estratégias de posicionamento de dados no craps. Alguns acreditam que é possível posicionar os dados de uma certa maneira antes do lançamento e, mantendo o movimento dos dados em apenas um eixo de rotação, diminuir a probabilidade de sair o número sete com determinadas configurações. Gostaria de saber se isso tem algum fundamento ou se é apenas um mito.

Duane de Las Vegas, USA

Eu não acredito nisso. Até agora, não vi nenhum nome que eu respeite endossar o método, nem qualquer evidência de que funcione. Embora eu não descarte completamente a possibilidade, sou extremamente cético. Posso morar em Nevada, mas quando se trata de coisas como manipulação de dados, sou do Missouri: "mostre-me" que funciona.
Os dados são realmente imparciais? Parece que os lados com os números maiores, que têm mais furos, seriam mais leves do que os lados com os números menores e menos furos. Isso sugere que os lados mais pesados teriam maior probabilidade de cair com a face para baixo, enquanto os números maiores teriam maior probabilidade de cair com a face para cima. Posso imaginar um sistema de craps que tentasse explorar esse princípio, mas me pergunto se funcionaria na prática. O que você acha?

Samuel de USA

Com dados comuns, como os de jogos de tabuleiro, isso é verdade. No entanto, os dados de cassino têm pontos embutidos. Na fábrica, eles fazem furos para os pontos e inserem pontos brancos nesses furos, com a mesma densidade do próprio dado. Assim, o dado é essencialmente um cubo perfeito. Mesmo que usassem dados comuns de jogos de tabuleiro, duvido que a diferença fosse suficiente para superar a vantagem da casa.
Você acredita que o lançamento de dados em uma mesa de Craps de cassino é verdadeiramente aleatório como seria um gerador de números aleatórios (RNG), ou existem jogadores bons e ruins, seja por "mecânica" dos dados ou simplesmente por lançamentos descuidados (lançamentos curtos, por exemplo)? Se o Craps de cassino no mundo real não é verdadeiramente aleatório, como eu poderia tirar proveito disso?

anônimo

Acredito que não existe um jogador de dados naturalmente ruim. Com a possível exceção de alguns profissionais, todos os lançamentos de dados podem ser considerados verdadeiramente aleatórios. Existem seminários sobre como superar a vantagem da casa no craps através de lançamentos precisos, mas não faço nenhuma afirmação a favor ou contra eles. Ainda não vi evidências suficientes em nenhum dos sentidos.
Na edição de outubro da revista Casino Player, Frank Scoblete escreveu um artigo sobre controle de dados, no qual você afirma ter perdido US$ 1.800 para Stanford Wong, que tirou apenas 74 setes em 500 lançamentos. Por que você apostou em uma amostra tão pequena (500)? Uma pessoa que alega ser capaz de controlar os dados deveria estar disposta a demonstrar sua habilidade com pelo menos 50.000 lançamentos. Estou errado em pensar que 500 lançamentos é uma amostra tão pequena que praticamente qualquer coisa pode acontecer?

Gerald de Alexandria

Perdi os US$ 1.800 para outro jornalista especializado em jogos de azar, não para Stanford. Eu teria preferido mais lançamentos, mas havia uma óbvia limitação de tempo. Supondo um lançamento por minuto, levaria 34,7 dias para lançar os dados 50.000 vezes. Não fui eu quem decidiu por 500, mas pareceu um compromisso razoável entre uma amostra grande e o tempo disponível. Você tem razão ao dizer que 500 é um número muito pequeno para se chegar a uma conclusão definitiva a favor ou contra a influência nos dados, mas 500 lançamentos são melhores do que nenhum.
Sei que você é cético quanto ao controle dos dados. Venho praticando posicionamento e lançamento controlado de dados há 3 meses. Qual a probabilidade de tirar 78 setes em 655 lançamentos aleatórios? Obrigado pela ajuda :)

Eric B. de Boston, MA

Para um grande número de lançamentos, podemos usar a aproximação da Curva Gaussiana. O número esperado de setes em 655 lançamentos é 655 × (1/6) = 109,1667. A variância é 655 × (1/6) × (5/6) = 90,9722. O desvio padrão é sqr(90,9722) = 9,5379. Seus 78 setes representam 109,1667 − 78 = 31,1667 a menos do que o esperado. Isso é (31,1667 - 0,5)/9,5379 = 3,22 desvios padrão abaixo do esperado. A probabilidade de ficar 3,22 ou mais desvios padrão abaixo do esperado é 0,000641, ou 1 em 1.560. Obtive esse valor no Excel, usando a fórmula DIST.NORMAS(-3,22).
Trata-se do controle dos dados no Craps. Você mencionou anteriormente o Experimento de Stanford Wong , afirmando: "Os termos da aposta eram se jogadores de precisão conseguiriam rolar menos de 79,5 setes em 500 lançamentos de dados. O número esperado em um jogo aleatório seria 83,33. A probabilidade de rolar 79 ou menos setes em 500 lançamentos aleatórios é de 32,66%... A probabilidade de rolar 74 ou menos setes em 500 lançamentos aleatórios é de 14,41%."

A minha dúvida em relação a essa aposta é que 14,41% ainda não é "estatisticamente significativo" [ou seja, p < 0,05], o que geralmente significa mais de dois desvios padrão da média — ou uma probabilidade inferior a 5% de o evento ocorrer aleatoriamente em QUALQUER uma das extremidades da série.

Quantos setes teriam que ser obtidos em 500 lançamentos para que se pudesse afirmar que há menos de 2,5% de chance de o resultado ser totalmente aleatório (ou seja, que o resultado seja estatisticamente significativo)?

Muito obrigado! Aliás, o seu site é simplesmente o melhor que já encontrei sobre probabilidades e probabilidades de jogos de azar... continue com o ótimo trabalho!

Plexus de Warwick, Rhode Island

Obrigado pelas gentis palavras. Você não deveria afirmar que a probabilidade de os lançamentos não serem aleatórios é p. A forma correta de dizer é que a probabilidade de um jogo aleatório produzir tal resultado é p. Ninguém esperava que 500 lançamentos provassem ou refutassem algo. Não fui eu quem definiu a linha em 79,5 setes, mas duvido que tenha sido escolhida por ser estatisticamente significativa; suspeito que tenha sido um ponto em que ambas as partes concordariam com a aposta.

O nível de significância de 2,5% corresponde a 1,96 desvios padrão abaixo do esperado. Isso pode ser calculado com a fórmula =normsinv(0,025) no Excel. O desvio padrão de 500 lançamentos é sqr(500*(1/6)*(5/6)) = 8,333. Portanto, 1,96 desvios padrão correspondem a 1,96 * 8,333 = 16,333 lançamentos abaixo do esperado. O número esperado de setes em 500 lançamentos é 500*(1/6) = 83,333. Assim, 1,96 desvios padrão abaixo desse valor correspondem a 83,333 − 16,333 = 67. Verificando isso usando a distribuição binomial, a probabilidade exata de 67 ou menos setes é de 2,627%.

Há três anos, em uma coluna "Pergunte ao Mago" , você escreveu: "Você está certo ao dizer que 500 lançamentos são poucos para se ter uma boa ideia a favor ou contra a influência nos dados, mas 500 lançamentos são melhores que zero." Você poderia descrever o que exigiria de um suposto influenciador de dados, em um experimento, para que você se sentisse confiante o suficiente para começar a apostar quantias significativas de dinheiro nele? Pergunto isso porque um bilhão de rodadas é um bom parâmetro para resultados "confiáveis" em alguns simuladores de blackjack. Com o design experimental mais eficiente (ou seja, que exige o menor número de lançamentos) que você consegue imaginar, quantos lançamentos o lançador precisaria fazer para ter certeza de que está influenciando os resultados? Sei que a resposta dependerá da habilidade do lançador, mas você entendeu a ideia. Se forem necessários um milhão de lançamentos, mesmo no melhor cenário, não valerá a pena.

Myooligan de Greenfelt

Não existe um ponto definitivo em que se conquista a confiança. É uma questão de grau. Primeiro, eu perguntaria o que está sendo testado e o que o atirador estima que acontecerá. Em qualquer teste, existem dois erros possíveis. Um atirador habilidoso pode falhar por azar, ou um atirador aleatório pode passar por sorte. Entre os dois, eu preferiria evitar um falso positivo. Acho que um teste razoável definiria a probabilidade de um falso negativo em cerca de 5% e a de um falso positivo em cerca de 1%.

Por exemplo, suponha que o requerente diga que consegue, em média, um total de sete a cada sete lançamentos de dados. Um lançador aleatório obteria um sete a cada seis lançamentos, em média. Por tentativa e erro, descobri que um teste que atendesse a ambos os critérios seria lançar os dados 3.600 vezes e exigir 547 ou menos setes para aprovação, ou um sete a cada 6,58 lançamentos.

Um atirador com uma probabilidade de 1 em 7 deveria acertar em média 514,3 setes, com um desvio padrão de 21,00. Usando a aproximação gaussiana, a probabilidade de um atirador habilidoso acertar 548 ou mais setes (um falso negativo) é de 5,7%. Um atirador aleatório deveria acertar em média 600 setes, com um desvio padrão de 22,36. A probabilidade de um atirador aleatório passar no teste (um falso positivo) é de 0,94%. O gráfico abaixo mostra os possíveis resultados para atiradores habilidosos e aleatórios. Se os resultados estiverem à esquerda da linha verde, eu consideraria que o atirador passou no teste e apostaria nele.

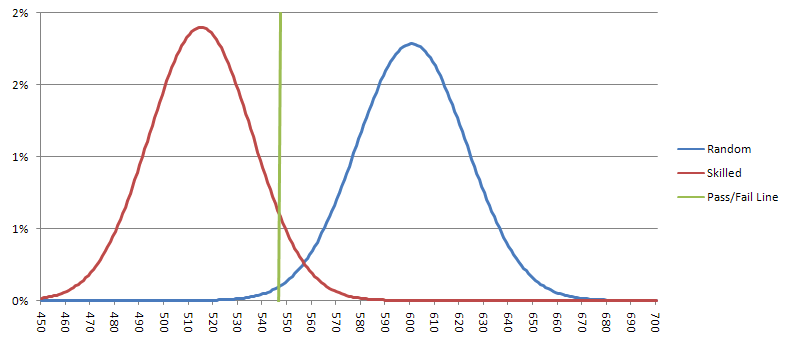
O dilema prático é que, se assumirmos dois lançamentos por minuto, levaria 30 horas para realizar o teste. Talvez eu pudesse ser mais flexível quanto ao nível de significância, para reduzir o tempo necessário, mas os resultados não seriam tão convincentes. Acho que chegou a hora de um teste maior do que o experimento de Wong com 500 lançamentos.

Hoje, as notícias contam que uma mulher em Atlantic City rolou 154 dados consecutivos antes de tirar um sete no Borgata . Isso significa que ela rolou dois dados 154 vezes, sem nenhum sete. Então, calculei (30/36) 154 e cheguei a uma probabilidade de mais de 1,5 trilhão para 1. É cerca de 9.000 vezes mais provável ganhar na loteria Mega Millions do que conseguir uma maratona de 154 lançamentos consecutivos de dados sem tirar o sete. Considerando o quão astronomicamente improvável isso é, e considerando que pessoas são condenadas com base em evidências de DNA com probabilidades de bilhões para um de serem falsas, o quanto você suspeitaria de fraude e se ofereceria para consultar o Borgata sobre isso? Eu já liguei para eles, dei meu nome e disse para fazerem o que quiserem com a informação. Gostaria de saber sua opinião.

Adam

Primeiramente, ela lançou os dados um total de 154 vezes, sendo que o 154º lançamento resultou em um sete ( Fonte: NJ.com ). No entanto, isso não significa que ela nunca tenha tirado um sete nos primeiros 153 lançamentos. Ela poderia ter tirado muitos deles nos lançamentos iniciais. Como mostrei em minha coluna de 3 de maio de 2003 , a probabilidade de chegar ao 154º lançamento é de 1 em 5,6 bilhões. As chances de ganhar na Mega Millions são de 1 em combin (56,5)*46 = 175.711.536. Portanto, chegar a 154 lançamentos ou mais é cerca de 32 vezes mais difícil. Dado tempo suficiente e tabelas, que acredito existirem, algo assim acabaria acontecendo mais cedo ou mais tarde. Então, eu não suspeitaria de trapaça. Estimo que a probabilidade de isso acontecer em qualquer ano seja de aproximadamente 1%.

Veja também minha solução, expressa em matrizes, em mathproblems.info , problema 204.

Acredito que alguns cassinos em Las Vegas estejam usando dados viciados em um dos lados. Como prova, apresento os resultados de 244 lançamentos que coletei em um cassino da Strip. Qual a probabilidade de resultados tão distorcidos virem de dados honestos?

Dados do teste de dados
Total de dados Observações
2 6
3 12
4 14
5 18
6 23
7 50
8 36
9 37
10 27
11 14
12 7
Total 244

C. de Las Vegas

7,7%.

O teste qui-quadrado é perfeitamente adequado para esse tipo de questão. Para usar o teste, calcule (ae) ² /e para cada categoria, onde a é o resultado real e e é o resultado esperado. Por exemplo, o número esperado de lançamentos que totalizam 2 em 244 lançamentos é 244 × (1/36) = 6,777778. Se você não entende por que a probabilidade de rolar um 2 é 1/36, leia minha página sobre os fundamentos da probabilidade em dados . Para o valor qui-quadrado para um total de 2, a = 6 e e = 6,777778, então (ae) ² /e = (6 - 6,777778) ² /6,777778 = 0,089253802.

Resultados do Qui-Quadrado

Total de dados Observações Esperado Qui-quadrado
2 6 6,777778 0,089253
3 12 13,555556 0,178506
4 14 20,333333 1,972678
5 18 27.111111 3,061931
6 23 33,888889 3,498725
7 50 40,666667 2,142077
8 36 33,888889 0,131512
9 37 27.111111 3.607013
10 27 20,333333 2,185792
11 14 13,555556 0,014572
12 7 6,777778 0,007286
Total 244 244 16,889344

Em seguida, some os valores da coluna qui-quadrado. Neste exemplo, a soma é 16,889344. Esse valor é chamado de estatística qui-quadrado. O número de "graus de liberdade" é um a menos que o número de categorias nos dados, neste caso 11 - 1 = 10. Por fim, você pode consultar uma tabela estatística para encontrar um valor de qui-quadrado de 10,52 com 10 graus de liberdade ou usar a fórmula =DIST.QUI(16,889344;10) no Excel. Qualquer uma das opções resultará em 7,7%. Isso significa que a probabilidade de dados honestos produzirem resultados tão assimétricos ou mais é de 7,7%. Em resumo, embora esses resultados sejam mais assimétricos do que o esperado, a assimetria não é suficiente para causar preocupação. Se você continuar este teste, sugiro coletar o resultado individual de cada dado, em vez da soma. Deve-se notar também que o teste qui-quadrado não é apropriado se o número esperado de resultados de uma categoria for baixo. Uma expectativa mínima de 5 é um valor comumente mencionado.

O que aconteceria se os dois dados caíssem empilhados no craps? Seria um lançamento válido? Se sim, como os crupiês revelariam o número em que o dado de baixo parou?

boxman4

O fato de uma rolagem ser considerada válida ou não depende do local. O regulamento de jogos de Nova Jersey 19:47-1.9(a) afirma:

Um lançamento de dados será inválido sempre que um ou ambos os dados saírem da mesa ou sempre que um dado parar sobre o outro. -- NJ 19:47-1.9(a)

A Pensilvânia possui exatamente a mesma regulamentação, Seção 537.9(a) :

Um lançamento de dados será inválido sempre que um ou ambos os dados saírem da mesa ou sempre que um dado parar sobre o outro. -- PA 537.9(a)

Perguntei a um crupiê de dados de Las Vegas, que me disse que lá seria considerado um lançamento válido, desde que fosse um lançamento correto. Embora ele nunca tenha visto isso acontecer, disse que, se acontecesse, os crupiês simplesmente moveriam o dado de cima para ver em que número o dado de baixo pararia. No entanto, é possível determinar o resultado do dado de baixo sem tocar ou olhar através do dado de cima. Veja como fazer. Primeiro, observando os quatro lados, você pode reduzir as possibilidades do dado de cima a duas. Veja como determinar o resultado com base nessas três possibilidades.

  • 1 ou 6: Procure o 3. Se o ponto mais alto estiver adjacente ao 5, o 1 está em cima. Caso contrário, se estiver adjacente ao 2, o 6 está em cima.
  • 2 ou 5: Procure o 3. Se o ponto mais alto estiver adjacente ao 6, o 2 está em cima. Caso contrário, se estiver adjacente ao 1, o 5 está em cima.
  • 3 ou 4: Procure o 2. Se o ponto mais alto estiver adjacente ao 6, o 3 está em cima. Caso contrário, se estiver adjacente ao 1, o 4 está em cima.

Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .

Qual é o número esperado de lançamentos de dois dados para que cada total entre 2 e 12 ocorra pelo menos uma vez?

SixHorse

Esta pergunta foi feita no TwoPlusTwo.com e respondida corretamente por BruceZ . A solução a seguir utiliza o mesmo método que BruceZ, a quem todo o crédito é devido. É uma resposta complexa, portanto, preste atenção.

  1. Primeiro, considere o número esperado de lançamentos para obter um total de dois. A probabilidade de sair um dois é de 1/36, então seriam necessários, em média, 36 lançamentos para obter os primeiros 2.

  2. Em seguida, considere o número esperado de lançamentos para obter um dois e um três. Já sabemos que serão necessários, em média, 36 lançamentos para obter o dois. Se o três for obtido enquanto se espera pelo dois, não serão necessários lançamentos adicionais para obtê-lo. No entanto, caso contrário, os dados precisarão ser lançados mais vezes para se obter o três.

    A probabilidade de sair um três é 1/18, então seriam necessárias, em média, 18 jogadas adicionais para obter o três, caso o dois saísse primeiro. Dado que há 1 maneira de sair o dois e 2 maneiras de sair o três, a probabilidade de o dois sair primeiro é 1/(1+2) = 1/3.

    Portanto, há 1/3 de chance de precisarmos das 18 jogadas extras para conseguirmos o três. Assim, o número esperado de jogadas para conseguirmos um dois e um três é 36 + (1/3) × 18 = 42.

  3. Em seguida, considere quantas jogadas a mais você precisará para tirar um quatro. Se, ao jogar o dois e o três, você ainda não tiver tirado um quatro, precisará jogar os dados mais 12 vezes, em média, para conseguir um. Isso ocorre porque a probabilidade de sair um quatro é de 1/12.

    Qual é a probabilidade de obter o quatro antes de obter o dois e o três? Primeiro, vamos revisar uma regra comum de probabilidade para quando A e B não são mutuamente exclusivos:

    pr(A ou B) = pr(A) + pr(B) - pr(A e B)

    Você subtrai pr(A e B) porque essa contingência é contada duas vezes em pr(A) + pr(B). Portanto,

    pr(4 antes de 2 ou 3) = pr(4 antes de 2) + pr(4 antes de 3) - pr(4 antes de 2 e 3) = (3/4)+(3/5)-(3/6) = 0,85.

    A probabilidade de não obter o quatro no caminho para o dois e o três é 1,0 - 0,85 = 0,15. Portanto, há 15% de chance de precisar das 12 jogadas extras. Assim, o número esperado de jogadas para obter um dois, um três e um quatro é 42 + 0,15 * 12 = 43,8.

  4. Em seguida, considere quantas jogadas a mais você precisará para tirar um cinco. Se, ao jogar os dados de dois a quatro, você ainda não tiver tirado um cinco, precisará jogar os dados mais 9 vezes, em média, para conseguir um, pois a probabilidade de sair um cinco é 4/36 = 1/9.

    Qual a probabilidade de se obter o cinco antes de se obter o dois, o três ou o quatro? A regra geral é:

    pr(A ou B ou C) = pr(A) + pr(B) + pr(C) - pr(A e B) - pr(A e C) - pr(B e C) + pr(A, B e C)

    Portanto, pr(5 antes de 2 ou 3 ou 4) = pr(5 antes de 2) + pr(5 antes de 3) + pr(5 antes de 4) - pr(5 antes de 2 e 3) - pr(5 antes de 2 e 4) - pr(5 antes de 3 e 4) + pr(5 antes de 2, 3 e 4) = (4/5) + (4/6) + (4/7) - (4/7) - (4/8) - (4/9) + (4/10) = 83/90. A probabilidade de não obter o quatro no caminho para o dois até o quatro é 1 - 83/90 = 7/90. Assim, há uma chance de 7,78% de precisar das 7,2 jogadas extras. Portanto, o número esperado de jogadas para obter um dois, três, quatro e cinco é 43,8 + (7/90)*9 = 44,5.

  5. Continue com a mesma lógica para totais de seis a doze. O número de cálculos necessários para encontrar a probabilidade de obter o próximo número antes que ele seja necessário como o último número dobra aproximadamente a cada vez. Quando você chegar ao doze, terá que fazer 1.023 cálculos.

    Eis a regra geral para pr(A ou B ou C ou ... ou Z)

    pr(A ou B ou C ou ... ou Z) =
    pr(A) + pr(B) + ... + pr(Z)
    - pr(A e B) - pr(A e C) - ... - pr(Y e Z) Subtraia a probabilidade de cada combinação de dois eventos
    + pr(A e B e C) + pr(A e B e D) + ... + pr(X e Y e Z) Some a probabilidade de cada combinação de três eventos
    - pr(A e B e C e D) - pr(A e B e C e E) - ... - pr(W e X e Y e Z) Subtraia a probabilidade de cada combinação de quatro eventos

    Em seguida, continue repetindo o processo, lembrando-se de somar a probabilidade para eventos com número ímpar de eventos e subtrair a probabilidade para eventos com número par de eventos. Obviamente, isso se torna tedioso para um grande número de eventos possíveis, praticamente exigindo uma planilha ou um programa de computador.

A tabela a seguir mostra o número esperado para cada etapa do processo. Por exemplo, 36 para obter um dois, 42 para obter um dois e um três. A célula inferior direita mostra que o número esperado de lançamentos para obter todos os 11 totais é 61,217385.

Problema do Número Esperado de Rolos

Número máximo necessário Probabilidade Rolagens esperadas, se necessário Probabilidade não necessária Probabilidade necessária Total de matrículas esperado
2 0,027778 36,0 0,000000 1.000000 36.000000
3 0,055556 18.0 0,666667 0,333333 42.000000
4 0,083333 12.0 0,850000 0,150000 43.800000
5 0,111111 9.0 0,922222 0,077778 44.500000
6 0,138889 7.2 0,956044 0,043956 44,816484
7 0,166667 6.0 0,973646 0,026354 44,974607
8 0,138889 7.2 0,962994 0,037006 45.241049
9 0,111111 9.0 0,944827 0,055173 45,737607
10 0,083333 12.0 0,911570 0,088430 46,798765
11 0,055556 18.0 0,843824 0,156176 49,609939
12 0,027778 36,0 0,677571 0,322429 61,217385

Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .

Segundo o siteCraps Advantage Players , os cassinos de Las Vegas usam dados viciados rotineiramente para aumentar a proporção de setes e, assim, aumentar os lucros. Estou incrédulo! O que o Mágico tem a dizer sobre isso?

Stephanie de Biloxi, MS

O Wizard diz que aquele site parece um amontoado de reclamações e desvarios sem qualquer evidência credível para justificar a acusação. Eu ficaria feliz em expor qualquer cassino por usar dados viciados, se tivesse qualquer prova disso.

Se alguém tiver provas legítimas de dados viciados, terei todo o prazer em analisá-las e publicar as minhas conclusões. As provas que gostaria de ver são registos de lançamentos ou, melhor ainda, alguns dados alegadamente viciados.

Além disso, se os cassinos realmente estivessem usando dados que produziam mais setes do que o esperado, por que esses detetives não têm conhecimento da conspiração que envolve apostar no "não passe" e manipular as probabilidades?
A rodada bônus Hot Roll em máquinas caça-níqueis premia o jogador com a seguinte quantidade de moedas, de acordo com o total de dois dados. O jogador continua acumulando até obter um total de sete, o que encerra o bônus. Se ele obtiver um sete na primeira rodada, recebe um prêmio de consolação de 70 moedas. A seguir, estão os prêmios para todos os outros totais diferentes de sete:

  • 2 ou 12: 1.000
  • 3 ou 11: 600
  • 4 ou 10: 400
  • 5 ou 9: 300
  • 6 ou 8: 200


Minha pergunta é: qual é o ganho médio de bônus?

anônimo

Clique no botão a seguir para ver a resposta.

A resposta é 1983,33.

Clique no botão a seguir para ver a solução.

Seja x a resposta. Enquanto o jogador não tirar um sete, ele sempre pode esperar que as vitórias futuras sejam x, além de todas as vitórias anteriores. Em outras palavras, existe uma propriedade de ausência de memória no lançamento de dados, de modo que, não importa quantas jogadas você já tenha feito, você não está mais perto de um sete do que estava quando começou.

Não vou entrar em detalhes sobre as probabilidades em dados, mas basta dizer que a probabilidade de cada total é a seguinte:
  • 2: 1/36
  • 3: 2/36
  • 4: 3/36
  • 5: 4/36
  • 6: 5/36
  • 7: 6/36
  • 8: 5/36
  • 9: 4/36
  • 10: 3/36
  • 11: 2/36
  • 12: 1/36


Antes de considerar o prêmio de consolação, o valor de x pode ser expresso como:

x = (1/36)*(1000 + x) + (2/36)*(600 + x) + (3/36)*(400 + x) + (4/36)*(300 + x) + (5/36)*(200 + x) + (5/36)*(200 + x) + (4/36)*(300 + x) + (3/36)*(400 + x) + (2/36)*(600 + x) + (1/36)*(1000 + x)

Em seguida, multiplique ambos os lados por 36:

36x = (1000 + x) + 2*(600 + x) + 3*(400 + x) + 4*(300 + x) + 5*(200 + x) + 5*(200 + x) + 4*(300 + x) + 3*(400 + x) + 2*(600 + x) + (1000 + x)

36x = 11.200 + 30x

6x = 11.200

x = 11.200/6 = 1866,67.

Em seguida, o valor do prêmio de consolação é 700*(6/36) = 116,67.

Assim, o ganho médio do bônus é de 1866,67 + 116,67 = 1983,33.