Recomendações do Mago
-
Bônus de boas-vindas de $11000 -
Bônus de boas-vindas de 3000 $ -
BÔNUS DE ATÉ $777
Probabilidade - Dados
Essas apostas podem ser feitas tanto no sic bo quanto no chuck a luck .
[Bluejay acrescenta: Ah, sim, mas acho que a questão era que era para caridade. O que é mais divertido: doar 1 libra para caridade e não receber nada em troca além da boa sensação de ajudar, ou doar 1 libra e ter a boa sensação mais a remota chance de ganhar um carro?]
- Cinco de um mesmo tipo: 6/6 5 = 0,08% (óbvio)
- Quadra: 5*6*5 = 1,93% (cinco posições possíveis para o singleton * 6 posições para a quadra * 5 posições para o singleton).
- Full house: combin(5,3)*6*5/6 5 = 3,86% (combin(5,3) posições para a trinca * 6 posições para a trinca * 2 posições para o par).
- Trinca: COMBIN(5,3)*COMBIN(2,1)*6*COMBIN(5,2) / 6 5 = 15,43%. (combin(5,3) posições para a trinca * combin(2,1) posições para o maior dos singletons * 6 posições da trinca * combin(5,2) posições para os dois singletons).
- Dois pares: COMBIN(5,2)*COMBIN(3,2)*COMBIN(6,2)*4 / 6 5 = 23,15% (combin(5,2) posições para o par superior * combin(3,2) posições para o par inferior * combin(6,4) posições para o par duplo * 4 posições para o singleton.
- Par: COMBIN(5,2)*fact(3)*6*combin(5,3) / 6 5 = 46,30% (combin(5,2) posições para o par * fact(3) posições para os três singletons * 6 ranks para o par * combin(5,3) ranks para os singletons.
- Direto: 2*fact(5) / 6 5 = 3,09% (2 intervalos para as maneiras diretas {1-5 ou 2-6} * fact(5) de organizar a ordem).
- Nada: ((COMBIN(6,5)-2)*FACT(5)) / 6 5 = 6,17% (combin(6,5) maneiras de escolher 5 posições entre seis, menos 2 para as sequências, * fact(5) maneiras de organizar a ordem.
w=1-(1-p) n
1-w = (1-p) n
log(1-w) = log((1-p) n )
log(1-w) = n*log(1-p)
n = log(1-w)/log(1-p)
Então, no seu exemplo, n = log(1-0,5) / log(1-(1/36)) = log(0,5) / log(35/36) = 24,6051. Portanto, se a probabilidade de sucesso é de 50% em 24,6 lançamentos, ela deve ser ligeiramente menor em 24 lançamentos.
3 dados: 25,93%
4 dados: 48,77%
5 dados: 66,13%.
Seja B = Obter um 6 ao rolar um dado escolhido aleatoriamente.
Resposta = Pr(A dado B) = Pr(A e B)/pr(B) = ((2/3)*(1/6))/((2/3)*(1/6)+(1/3)*1) = (2/18)/((2/18)+(6/18)) = 1/4.
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y), e
Ex(y) = 1 + (5/6)*ex(x)
Resolvendo essas duas equações...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*( 1 + (5/6)*Ex(x))
Ex(x) = 7/6 + (35/36)*Ex(x)
(1/36)*Ex(x) = 7/6
Ex(x) = 36*(7/6) = 42
Assim, o tempo médio de espera para dois números dois consecutivos é de 42 lançamentos.
Eu tenho o mesmo tipo de problema, só que com os lançamentos esperados para se obter duas caras, no meu site de problemas de matemática , veja o problema 128.
Probabilidade de um par ou mais
| Rolls | Probabilidade |
| 2 rolos | 16,67% |
| 3 rolos | 44,44% |
| 4 rolos | 72,22% |
| 5 rolos | 90,74% |
| 6 rolos | 98,46% |
(8/36) n = 1/41.400.000
log((8/36) n ) = log(1/41.400.000)
n × log(8/36) = log(1/41.400.000)
n = log(1/41.400.000)/log(8/36)
n = -7,617 / -0,65321
n = 11,6608
Então, pronto, a probabilidade de ganhar na SuperLotto é a mesma que tirar um sete ou um onze 11,66 vezes seguidas. Para quem não entende o conceito de lançamento parcial, eu reformularia dizendo que a probabilidade fica entre 11 e 12 lançamentos consecutivos.
Se dois dados forem lançados repetidamente até que um dos seguintes eventos ocorra, qual deles tem maior probabilidade de acontecer primeiro:
- É possível rolar um total de seis ou oito dados, em qualquer ordem, sendo permitidas duplicatas.
- O resultado de sete é obtido ao rolar o dado duas vezes.
Alguém me ofereceu uma aposta de que o seis e o oito sairiam primeiro. Aceitei porque sete é o total mais provável. No entanto, perdi US$ 2.500 fazendo isso repetidamente. Quais são as chances?
Dois setes antes de seis e oito apostas
| Rolos relevantes | Probabilidade | Fórmula | Resultado |
| 6,8 | 0,142045 | (5/16)*(5/11) | Perder |
| 8,6 | 0,142045 | (5/16)*(5/11) | Perder |
| 6,7,8 | 0,077479 | (5/16)*(6/11)*(5/11) | Perder |
| 7,6,8 | 0,053267 | (6/16)*(5/16)*(5/11) | Perder |
| 8,7,6 | 0,077479 | (5/16)*(6/11)*(5/11) | Perder |
| 7,8,6 | 0,053267 | (6/16)*(5/16)*(5/11) | Perder |
| 7,7 | 0,140625 | (6/16)*(6/16) | Ganhar |
| 6,7,7 | 0,092975 | (5/16)*(6/11)*(6/11) | Ganhar |
| 8,7,7 | 0,092975 | (5/16)*(6/11)*(6/11) | Ganhar |
| 7,6,7 | 0,06392 | (6/16)*(5/16)*(6/11) | Ganhar |
| 7,8,7 | 0,06392 | (6/16)*(5/16)*(6/11) | Ganhar |
Basicamente, a vantagem do 6 e do 8 reside no fato de que você pode acertar esses números em qualquer ordem: 6 e depois 8, ou 8 e depois 6. Com dois setes, só existe uma ordem possível: um 7 e depois outro 7.
A minha dúvida em relação a essa aposta é que 14,41% ainda não é "estatisticamente significativo" [ou seja, p < 0,05], o que geralmente significa mais de dois desvios padrão da média — ou uma probabilidade inferior a 5% de o evento ocorrer aleatoriamente em QUALQUER uma das extremidades da série.
Quantos setes teriam que ser obtidos em 500 lançamentos para que se pudesse afirmar que há menos de 2,5% de chance de o resultado ser totalmente aleatório (ou seja, que o resultado seja estatisticamente significativo)?
Muito obrigado! Aliás, o seu site é simplesmente o melhor que já encontrei sobre probabilidades e probabilidades de jogos de azar... continue com o ótimo trabalho!
O nível de significância de 2,5% corresponde a 1,96 desvios padrão abaixo do esperado. Isso pode ser calculado com a fórmula =normsinv(0,025) no Excel. O desvio padrão de 500 lançamentos é sqr(500*(1/6)*(5/6)) = 8,333. Portanto, 1,96 desvios padrão correspondem a 1,96 * 8,333 = 16,333 lançamentos abaixo do esperado. O número esperado de setes em 500 lançamentos é 500*(1/6) = 83,333. Assim, 1,96 desvios padrão abaixo desse valor correspondem a 83,333 − 16,333 = 67. Verificando isso usando a distribuição binomial, a probabilidade exata de 67 ou menos setes é de 2,627%.
Experimento Yahtzee
| Rolls | ocorrências | Probabilidade |
| 1 | 63908 | 0,00077371 |
| 2 | 977954 | 0,0118396 |
| 3 | 2758635 | 0,0333975 |
| 4 | 4504806 | 0,0545376 |
| 5 | 5776444 | 0,0699327 |
| 6 | 6491538 | 0,0785901 |
| 7 | 6727992 | 0,0814527 |
| 8 | 6601612 | 0,0799227 |
| 9 | 6246388 | 0,0756221 |
| 10 | 5741778 | 0,0695131 |
| 11 | 5174553 | 0,0626459 |
| 12 | 4591986 | 0,0555931 |
| 13 | 4022755 | 0,0487016 |
| 14 | 3492745 | 0,042285 |
| 15 | 3008766 | 0,0364257 |
| 16 | 2577969 | 0,0312103 |
| 17 | 2193272 | 0,0265529 |
| 18 | 1864107 | 0,0225679 |
| 19 | 1575763 | 0,019077 |
| 20 | 1329971 | 0,0161013 |
| 21 | 1118788 | 0,0135446 |
| 22 | 940519 | 0,0113864 |
| 23 | 791107 | 0,00957757 |
| 24 | 661672 | 0,00801056 |
| 25 | 554937 | 0,00671837 |
| 26 | 463901 | 0,00561624 |
| 27 | 387339 | 0,00468933 |
| 28 | 324079 | 0,00392347 |
| 29 | 271321 | 0,00328476 |
| 30 | 225978 | 0,00273581 |
| 31 | 189012 | 0,00228828 |
| 32 | 157709 | 0,00190931 |
| 33 | 131845 | 0,00159619 |
| 34 | 109592 | 0,00132678 |
| 35 | 91327 | 0,00110565 |
| 36 | 76216 | 0,00092271 |
| 37 | 63433 | 0,00076795 |
| 38 | 52786 | 0,00063906 |
| 39 | 44122 | 0,00053417 |
| 40 | 36785 | 0,00044534 |
| 41 | 30834 | 0,00037329 |
| 42 | 25494 | 0,00030864 |
| 43 | 21170 | 0,0002563 |
| 44 | 17767 | 0,0002151 |
| 45 | 14657 | 0,00017745 |
| 46 | 12410 | 0,00015024 |
| 47 | 10299 | 0,00012469 |
| 48 | 8666 | 0,00010492 |
| 49 | 7355 | 0,00008904 |
| 50 | 5901 | 0,00007144 |
| 51 | 5017 | 0,00006074 |
| 52 | 4227 | 0,00005117 |
| 53 | 3452 | 0,00004179 |
| 54 | 2888 | 0,00003496 |
| 55 | 2470 | 0,0000299 |
| 56 | 2012 | 0,00002436 |
| 57 | 1626 | 0,00001969 |
| 58 | 1391 | 0,00001684 |
| 59 | 1135 | 0,00001374 |
| 60 | 924 | 0,00001119 |
| 61 | 840 | 0,00001017 |
| 62 | 694 | 0,0000084 |
| 63 | 534 | 0,00000646 |
| 64 | 498 | 0,00000603 |
| 65 | 372 | 0,0000045 |
| 66 | 316 | 0,00000383 |
| 67 | 286 | 0,00000346 |
| 68 | 224 | 0,00000271 |
| 69 | 197 | 0,00000238 |
| 70 | 160 | 0,00000194 |
| 71 | 125 | 0,00000151 |
| 72 | 86 | 0,00000104 |
| 73 | 79 | 0,00000096 |
| 74 | 94 | 0.00000114 |
| 75 | 70 | 0,00000085 |
| 76 | 64 | 0,00000077 |
| 77 | 38 | 0,00000046 |
| 78 | 42 | 0,00000051 |
| 79 | 27 | 0,00000033 |
| 80 | 33 | 0,0000004 |
| 81 | 16 | 0,00000019 |
| 82 | 18 | 0,00000022 |
| 83 | 19 | 0,00000023 |
| 84 | 14 | 0,00000017 |
| 85 | 6 | 0,00000007 |
| 86 | 4 | 0,00000005 |
| 87 | 9 | 0,00000011 |
| 88 | 4 | 0,00000005 |
| 89 | 5 | 0,00000006 |
| 90 | 5 | 0,00000006 |
| 91 | 1 | 0,00000001 |
| 92 | 6 | 0,00000007 |
| 93 | 1 | 0,00000001 |
| 94 | 3 | 0,00000004 |
| 95 | 1 | 0,00000001 |
| 96 | 1 | 0,00000001 |
| 97 | 2 | 0,00000002 |
| 102 | 1 | 0,00000001 |
| Total | 82600000 | 1 |
No entanto, para fins práticos, existe um limite. Isso porque a felicidade que o dinheiro traz não é proporcional à quantidade. Embora seja geralmente aceito que mais dinheiro traz mais felicidade, quanto mais rico você fica, menos felicidade cada dólar adicional lhe proporciona.
Acredito que uma boa maneira de responder a essa pergunta seja aplicar o Critério de Kelly ao problema. Segundo Kelly, o jogador deve tomar todas as decisões com o objetivo de maximizar o logaritmo esperado de sua banca após a aposta. Resumindo (omitindo muitos cálculos), o jogador deve continuar dobrando a aposta até que o valor total ultrapasse 96,5948% de sua riqueza total. Riqueza deve ser definida como a soma do valor ganho mais o dinheiro que o jogador possuía antes da primeira aposta. Por exemplo, se o jogador tinha US$ 100.000 inicialmente, ele deve continuar dobrando a aposta até 23 vezes, até um ganho de US$ 4.194.304. Nesse ponto, a riqueza total do jogador será de US$ 4.294.304. Será solicitado a ele que aposte 4.194.304/4.294.304 = 96,67% de sua riqueza total, o que é maior que o ponto de parada de 96,5948%, portanto ele deve desistir.
p = Prob(6 no primeiro lançamento) + Prob(nenhum 6 no primeiro lançamento)*Prob(nenhum 7 no segundo lançamento)*p.
Isso ocorre porque, se nenhum dos jogadores vencer após as duas primeiras rodadas, o jogo retorna ao estado original e a probabilidade de o jogador A vencer permanece a mesma.
Então, temos:
p = (5/36) + (31/36)×(30/36)×p
p = 5/36 + (930/1296)×p
p * (1-(930/1296)) = 5/36.
p * (366/1296) = 5/36
p = (5/36)×(1296/366) = 30/61.
Combinações de dados não distintas
| Dados | Combinações |
| 1 | 6 |
| 2 | 21 |
| 3 | 56 |
| 4 | 126 |
| 5 | 252 |
| 6 | 462 |
| 7 | 792 |
| 8 | 1287 |
| 9 | 2002 |
| 10 | 3003 |
| 11 | 4368 |
| 12 | 6188 |
| 13 | 8568 |
| 14 | 11628 |
| 15 | 15504 |
| 16 | 20349 |
| 17 | 26334 |
| 18 | 33649 |
| 19 | 42504 |
| 20 | 53130 |
| 21 | 65780 |
| 22 | 80730 |
| 23 | 98280 |
Créditos a Alan Tucker, autor de Combinatória Aplicada .
Dois setes em sequência?
Três setes em sequência?
Quatro setes em sequência?
Obrigado pelo seu tempo :-).
É um pouco mais fácil obter uma sequência específica de setes começando com o primeiro lançamento ou terminando com o último, porque a sequência é limitada de um lado. Especificamente, a probabilidade de obter uma sequência de s setes, começando com o primeiro lançamento ou terminando com o último, é (1/6) s × (5/6). O termo 5/6 se deve ao fato de que você precisa obter um número diferente de 7 na extremidade aberta da sequência.
A probabilidade de iniciar uma sequência de s setes em qualquer ponto no meio da sequência é (1/6) s × (5/6) 2 . Elevamos o termo 5/6 ao quadrado, porque o jogador deve obter um número diferente de 7 em ambas as extremidades da sequência.
Se houver r lançamentos, haverá 2 posições para uma sequência interna e rn-1 posições para uma sequência de n setes. Colocando essas equações em uma tabela, temos o número esperado de sequências de setes, de 1 a 10. A coluna "interna" é 2*(5/6)*(1/6) r , e a coluna "externa" é (179-r)*(5/6) 2 *(1/6) r , onde r é o número de setes na sequência. Portanto, podemos esperar 3,46 sequências de dois setes, 0,57 sequências de três setes e 0,10 sequências de quatro setes.
Sequências esperadas de setes em 180 lançamentos
| Correr | Dentro | Fora | Total |
| 1 | 0,277778 | 20,601852 | 20,87963 |
| 2 | 0,046296 | 3,414352 | 3,460648 |
| 3 | 0,007716 | 0,565844 | 0,57356 |
| 4 | 0,001286 | 0,093771 | 0,095057 |
| 5 | 0,000214 | 0,015539 | 0,015754 |
| 6 | 0,000036 | 0,002575 | 0,002611 |
| 7 | 0,000006 | 0,000427 | 0,000433 |
| 8 | 0,000001 | 0,000071 | 0,000072 |
| 9 | 0 | 0,000012 | 0,000012 |
| 10 | 0 | 0,000002 | 0,000002 |
|
Se você se limitar aos polígonos regulares e quiser que cada face tenha a mesma probabilidade, então estará limitado aos sólidos platônicos. No entanto, se puder eliminar a restrição dos polígonos regulares, poderá adicionar também os 13 sólidos catalães .
Para responder à sua outra pergunta, não, nunca vi um jogo em um cassino que usasse dados que não fossem cubos. Há uns dez anos, vi uma demonstração de um jogo em uma feira de jogos em Atlantic City que, se não me engano, usava um triacontaedro rômbico , um dos sólidos catalães, mas acho que ele nunca chegou a ser usado em um cassino. Há um jogo que vejo ano após ano na Global Gaming Expo que usa um pião (como um dreidel), mas, infelizmente, também nunca o vi em um cassino.
Combinações em 4d6-L
| Resultado | Combinações |
| 3 | 1 |
| 4 | 4 |
| 5 | 10 |
| 6 | 21 |
| 7 | 38 |
| 8 | 62 |
| 9 | 91 |
| 10 | 122 |
| 11 | 148 |
| 12 | 167 |
| 13 | 172 |
| 14 | 160 |
| 15 | 131 |
| 16 | 94 |
| 17 | 54 |
| 18 | 21 |
| Total | 1296 |
O resultado médio é 12,2446 e o desvio padrão é 2,8468.
Se reformularmos a pergunta para qual a probabilidade de rolar cinco 6 antes de um 12, então a resposta é (6/7) 5 = 46,27%. Com quatro lançamentos, a probabilidade é (6/7) 4 = 53,98%. Portanto, não existe um número de 7 antes de um 12 que seja exatamente 50/50. Se você está procurando uma boa aposta para enganar os outros, sugira que você pode rolar quatro 7 antes de um 12, ou um 12 antes de cinco 7.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Probabilidades de um dado
| Total de dados | 1 | 2 | 3 | 4 | 5 | 6 | ||||||||||
| Um dado | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
Isso representa o número de combinações possíveis para rolar de 1 a 6 com um dado. Eu sei, é bem óbvio. Mas continue comigo. Para dois dados, adicione mais uma linha na parte inferior e, para cada célula, some a linha acima com as cinco células à esquerda. Em seguida, adicione mais cinco zeros fictícios à direita, se desejar continuar. Isso representa as combinações possíveis para rolar um total de 2 a 12.
Probabilidades de dois dados
| Total de dados | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||||||||||
| Um dado | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Dois dados | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 0 | 0 | 0 | 0 |
Para três dados, basta repetir. Isso representará o número de combinações de 3 a 18.
Para obter a probabilidade de qualquer total dado, divida o número de combinações desse total pelo número total de combinações. No caso de três dados, a soma é 216, que também pode ser facilmente calculada como 6³ . Por exemplo, a probabilidade de rolar um total de 13 com três dados é 21/216 = 9,72%.
Portanto, para dados d, você precisará calcular a quantidade de dados de 1 a d-1. Isso pode ser feito facilmente em qualquer planilha.
(35/36) r = 0,5
log(35/36) r = log(0,5)
r × log(35/36) = log(0,5)
r = log(0,5)/log(35/36)
r = 24,6051
Portanto, não há uma resposta arredondada. A probabilidade de tirar um 12 em 24 lançamentos é 1 - (35/36) 24 = 49,14%. A probabilidade de tirar um 12 em 25 lançamentos é 1 - (35/36) 25 = 50,55%.
Se você quiser apostar nisso, imagine que você consegue tirar um 12 em 25 lançamentos de dado, ou que outra pessoa não consegue em 24 lançamentos. De qualquer forma, você terá uma vantagem com odds de 1 para 1.
Para quem não conhece o jogo, tanto o atacante quanto o defensor rolam de 1 a 8 dados, de acordo com o número de exércitos que cada um possui naquele momento da batalha. Quem obtiver o maior total vence. Em caso de empate, a vitória é do defensor. Se o atacante perder, ele ainda manterá um exército no território onde iniciou o ataque. Por essa razão, ele precisa ter pelo menos dois exércitos para atacar, para que, se vencer, um possa ocupar o território conquistado e o outro possa permanecer no local original.
A tabela a seguir mostra a probabilidade de vitória do atacante de acordo com todas as 64 combinações possíveis de valores nos dados.
Probabilidade de vitória do atacante
| Atacante | Defensor | |||||||
|---|---|---|---|---|---|---|---|---|
| 1º Exército | 2 Exércitos | 3 Exércitos | 4 Exércitos | 5 Exércitos | 6 exércitos | 7 Exércitos | 8 exércitos | |
| 2 | 0,837963 | 0,443673 | 0,152006 | 0,035880 | 0,006105 | 0,000766 | 0,000071 | 0,000005 |
| 3 | 0,972994 | 0,778549 | 0,453575 | 0,191701 | 0,060713 | 0,014879 | 0,002890 | 0,000452 |
| 4 | 0,997299 | 0,939236 | 0,742831 | 0,459528 | 0,220442 | 0,083423 | 0,025450 | 0,006379 |
| 5 | 0,999850 | 0,987940 | 0,909347 | 0,718078 | 0,463654 | 0,242449 | 0,103626 | 0,036742 |
| 6 | 0,999996 | 0,998217 | 0,975300 | 0,883953 | 0,699616 | 0,466731 | 0,259984 | 0,121507 |
| 7 | 1.000000 | 0,999801 | 0,994663 | 0,961536 | 0,862377 | 0,685165 | 0,469139 | 0,274376 |
| 8 | 1.000000 | 0,999983 | 0,999069 | 0,989534 | 0,947731 | 0,843874 | 0,673456 | 0,471091 |
A próxima tabela mostra o ganho esperado do atacante, definido como pr(vitórias do atacante)*(dados do defensor)+pr(vitórias do defensor)*(dados do atacante -1). Ela mostra que o maior ganho esperado é atacar com 8 contra um oponente com 5.
Ganho líquido da vitória do atacante
| Atacante | Defensor | |||||||
|---|---|---|---|---|---|---|---|---|
| 1º Exército | 2 Exércitos | 3 Exércitos | 4 Exércitos | 5 Exércitos | 6 exércitos | 7 Exércitos | 8 exércitos | |
| 2 | 0,675926 | 0,331019 | -0,391976 | -0,820600 | -0,963370 | -0,994638 | -0,999432 | -0,999955 |
| 3 | 0,918982 | 1,114196 | 0,267875 | -0,849794 | -1,575009 | -1,880968 | -1,973990 | -1,995480 |
| 4 | 0,989196 | 1,696180 | 1,456986 | 0,216696 | -1,236464 | -2,249193 | -2,745500 | -2,929831 |
| 5 | 0,999250 | 1,927640 | 2,365429 | 1,744624 | 0,172886 | -1,575510 | -2,860114 | -3,559096 |
| 6 | 0,999976 | 1,987519 | 2,802400 | 2,955577 | 1,996160 | 0,134041 | -1,880192 | -3,420409 |
| 7 | 1.000000 | 1,998408 | 2,951967 | 3,615360 | 3,486147 | 2,221980 | 0,098807 | -2,158736 |
| 8 | 1.000000 | 1,999847 | 2,990690 | 3,884874 | 4,372772 | 3,970362 | 2,428384 | 0,066365 |
O jogador pode rolar novamente os dados que já havia obtido, se desejar. Por exemplo, se o primeiro lançamento do jogador for 3-3-4-5-6 e ele mantiver os três, e depois obtiver 3-3-5-5-5 após o segundo lançamento, ele pode manter os cincos e rolar novamente os três no terceiro lançamento.
A tabela a seguir mostra o número máximo de dados com a mesma face em 1 a 20 lançamentos. A tabela mostra que a probabilidade de obter um Yahtzee em três lançamentos é de aproximadamente 4,6%.
Probabilidades do Yahtzee
| Rolls | Número máximo de dados com a mesma face | ||||
|---|---|---|---|---|---|
| Um | Dois | Três | Quatro | Cinco | |
| 1 | 0,092593 | 0,694444 | 0,192901 | 0,019290 | 0,000772 |
| 2 | 0,008573 | 0,450103 | 0,409022 | 0,119670 | 0,012631 |
| 3 | 0,000794 | 0,256011 | 0,452402 | 0,244765 | 0,046029 |
| 4 | 0,000074 | 0,142780 | 0,409140 | 0,347432 | 0,100575 |
| 5 | 0,000007 | 0,079373 | 0,337020 | 0,413093 | 0,170507 |
| 6 | 0,000001 | 0,044101 | 0,263441 | 0,443373 | 0,249085 |
| 7 | 0,000000 | 0,024501 | 0,199279 | 0,445718 | 0,330502 |
| 8 | 0,000000 | 0,013612 | 0,147462 | 0,428488 | 0,410438 |
| 9 | 0,000000 | 0,007562 | 0,107446 | 0,398981 | 0,486011 |
| 10 | 0,000000 | 0,004201 | 0,077416 | 0,362855 | 0,555528 |
| 11 | 0,000000 | 0,002334 | 0,055317 | 0,324175 | 0,618174 |
| 12 | 0,000000 | 0,001297 | 0,039279 | 0,285674 | 0,673750 |
| 13 | 0,000000 | 0,000720 | 0,027757 | 0,249063 | 0,722460 |
| 14 | 0,000000 | 0,000400 | 0,019543 | 0,215313 | 0,764744 |
| 15 | 0,000000 | 0,000222 | 0,013720 | 0,184883 | 0,801175 |
| 16 | 0,000000 | 0,000124 | 0,009610 | 0,157896 | 0,832371 |
| 17 | 0,000000 | 0,000069 | 0,006719 | 0,134258 | 0,858954 |
| 18 | 0,000000 | 0,000038 | 0,004692 | 0,113753 | 0,881517 |
| 19 | 0,000000 | 0,000021 | 0,003272 | 0,096100 | 0,900607 |
| 20 | 0,000000 | 0,000012 | 0,002280 | 0,080994 | 0,916714 |
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
Um pouco fora do assunto, mas sempre achei que um conjunto de apostas par/ímpar seria uma boa maneira de substituir as temidas apostas altas de 6/8 no craps. Para dar vantagem à casa, aqui estão minhas tabelas de pagamento e análises propostas.
Aposta Ímpar
| Evento | Paga | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| 3 ou 11 | 1,5 | 4 | 0,111111 | 0,166667 |
| 5 ou 9 | 1 | 8 | 0,222222 | 0,222222 |
| 7 | 0,5 | 6 | 0,166667 | 0,083333 |
| Até | -1 | 18 | 0,500000 | -0,500000 |
| Total | 36 | 1.000000 | -0,027778 |
Aposta igual
| Evento | Paga | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| 2 ou 12 | 3 | 2 | 0,055556 | 0,166667 |
| 4 ou 10 | 1 | 6 | 0,166667 | 0,166667 |
| 6 ou 8 | 0,5 | 10 | 0,277778 | 0,138889 |
| Chance | -1 | 18 | 0,500000 | -0,500000 |
| Total | 36 | 1.000000 | -0,027778 |
Por favor, note que reivindico todos os direitos sobre esta publicação.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
- 2 ou 12: 1000
- 3 ou 11: 600
- 4 ou 10: 400
- 5 ou 9: 300
- 6 ou 8: 200
Ele continua jogando os dados até obter um total de sete, o que encerra o bônus. Se ele tirar um sete na primeira jogada, recebe um prêmio de consolação de 700 moedas. Qual é a média de moedas ganhas por bônus?
A seguir, apresentamos a probabilidade de cada total, assumindo que não haja sete:
- 2 ou 12: 1/30
- 3 ou 11: 2/30
- 4 ou 10: 3/30
- 5 ou 9: 4/30
- 6 ou 8: 5/30
Portanto, o ganho médio por lançamento, assumindo que não haja sete, é 2*[(1/30)*1000 + (2/30)*600 + (3/30)*400 + (4/30)*300 + (5/30)*200] = 373,33.
O valor do prêmio de consolação é (1/6)*700 = 116,67.
Assim, o ganho médio de bônus é 116,67 + 5×373,33 = 1983,33.
Qual seria a resposta para o problema dos dados na coluna Pergunte ao Mago nº 179 , se os jogadores se revezassem lançando os dados e apenas o jogador que lançasse pudesse avançar com base no resultado?
Eis a pergunta original postada na coluna nº 179: Se dois dados forem lançados repetidamente até que um dos seguintes eventos ocorra, qual deles tem maior probabilidade de acontecer primeiro:
- É possível rolar um total de seis ou oito dados, em qualquer ordem, sendo permitidas duplicatas.
- O resultado de sete é obtido ao rolar o dado duas vezes.
A sua peculiaridade é que o mesmo dado não pode beneficiar ambos os jogadores. Em vez disso, eles se revezam rolando os dados e apenas quem estiver rolando pode usar o resultado.
A resposta depende de quem joga primeiro. Se o jogador que precisa de um seis e um oito jogar primeiro, ele tem uma probabilidade de ganhar de 57,487294%. Se o jogador que precisa de dois setes jogar primeiro, a probabilidade de o jogador que precisa do seis e do oito ganhar é de 52,671614%. Resolvi o problema usando um processo simples de Cadeia de Markov.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Suponha que você tenha 12 dados de seis lados. Você os lança e pode separar quaisquer dados que desejar. Em seguida, você lança os dados restantes novamente. Qual é a probabilidade de obter uma sequência de 12 dados iguais nos dois lançamentos?
Existem 58 tipos diferentes de sequências na jogada inicial. A forma como identifico cada uma é pelo número da face majoritária, seguido pelo número total de dados com a mesma face em segundo lugar, e assim por diante. Por exemplo, uma jogada de 3,3,3,3,6,6,6,5,5,2 seria representada como 4-3-2-1. A tabela a seguir mostra o número de combinações de cada sequência, a probabilidade de obtê-la, a probabilidade de completar uma 12 de um mesmo tipo na segunda jogada e o produto das duas probabilidades. Para a probabilidade na segunda jogada, considero que o jogador possui os dados que têm o maior total na jogada inicial. A célula inferior direita mostra uma probabilidade geral de 0,0000037953, que equivale a 1 em 263.486.
Pergunta dos 12 dados
| Sequência | Combinações | Probabilidade Sequência | Condicional Probabilidade | Total Probabilidade |
|---|---|---|---|---|
| 12-0-0-0-0-0 | 6 | 0,0000000028 | 1,0000000000 | 0,0000000028 |
| 11-1-0-0-0-0 | 360 | 0,0000001654 | 0,1666666667 | 0,0000000276 |
| 10-2-0-0-0-0 | 1.980 | 0,0000009096 | 0,0277777778 | 0,0000000253 |
| 10-1-1-0-0-0 | 7.920 | 0,0000036384 | 0,0277777778 | 0,0000001011 |
| 9-3-0-0-0-0 | 6.600 | 0,0000030320 | 0,0046296296 | 0,0000000140 |
| 9-2-1-0-0-0 | 79.200 | 0,0000363840 | 0,0046296296 | 0,0000001684 |
| 9-1-1-1-0-0 | 79.200 | 0,0000363840 | 0,0046296296 | 0,0000001684 |
| 8-4-0-0-0-0 | 14.850 | 0,0000068220 | 0,0007716049 | 0,0000000053 |
| 8-3-1-0-0-0 | 237.600 | 0,0001091519 | 0,0007716049 | 0,0000000842 |
| 8-2-2-0-0-0 | 178.200 | 0,0000818639 | 0,0007716049 | 0,0000000632 |
| 8-2-1-1-0-0 | 1.069.200 | 0,0004911837 | 0,0007716049 | 0,0000003790 |
| 8-1-1-1-1-0 | 356.400 | 0,0001637279 | 0,0007716049 | 0,0000001263 |
| 7-5-0-0-0-0 | 23.760 | 0,0000109152 | 0,0001286008 | 0,0000000014 |
| 7-4-1-0-0-0 | 475.200 | 0,0002183039 | 0,0001286008 | 0,0000000281 |
| 7-3-2-0-0-0 | 950.400 | 0,0004366077 | 0,0001286008 | 0,0000000561 |
| 7-3-1-1-0-0 | 2.851.200 | 0,0013098232 | 0,0001286008 | 0,0000001684 |
| 7-2-2-1-0-0 | 4.276.800 | 0,0019647348 | 0,0001286008 | 0,0000002527 |
| 7-2-1-1-1-0 | 5.702.400 | 0,0026196464 | 0,0001286008 | 0,0000003369 |
| 7-1-1-1-1-1 | 570.240 | 0,0002619646 | 0,0001286008 | 0,0000000337 |
| 6-6-0-0-0-0 | 13.860 | 0,0000063672 | 0,0000214335 | 0,0000000001 |
| 6-5-1-0-0-0 | 665.280 | 0,0003056254 | 0,0000214335 | 0,0000000066 |
| 6-4-2-0-0-0 | 1.663.200 | 0,0007640635 | 0,0000214335 | 0,0000000164 |
| 6-4-1-1-0-0 | 4.989.600 | 0,0022921906 | 0,0000214335 | 0,0000000491 |
| 6-3-3-0-0-0 | 1.108.800 | 0,0005093757 | 0,0000214335 | 0,0000000109 |
| 6-3-2-1-0-0 | 19.958.400 | 0,0091687624 | 0,0000214335 | 0,0000001965 |
| 6-3-1-1-1-0 | 13.305.600 | 0,0061125083 | 0,0000214335 | 0,0000001310 |
| 6-2-2-2-0-0 | 4.989.600 | 0,0022921906 | 0,0000214335 | 0,0000000491 |
| 6-2-2-1-1-0 | 29.937.600 | 0,0137531436 | 0,0000214335 | 0,0000002948 |
| 6-2-1-1-1-1 | 9.979.200 | 0,0045843812 | 0,0000214335 | 0,0000000983 |
| 5-5-2-0-0-0 | 997.920 | 0,0004584381 | 0,0000035722 | 0.0000000016 |
| 5-5-1-1-0-0 | 2.993.760 | 0,0013753144 | 0,0000035722 | 0,0000000049 |
| 5-4-3-0-0-0 | 3.326.400 | 0,0015281271 | 0,0000035722 | 0,0000000055 |
| 5-4-2-1-0-0 | 29.937.600 | 0,0137531436 | 0,0000035722 | 0,0000000491 |
| 5-4-1-1-1-0 | 19.958.400 | 0,0091687624 | 0,0000035722 | 0,0000000328 |
| 5-3-3-1-0-0 | 19.958.400 | 0,0091687624 | 0,0000035722 | 0,0000000328 |
| 5-3-2-2-0-0 | 29.937.600 | 0,0137531436 | 0,0000035722 | 0,0000000491 |
| 5-3-2-1-1-0 | 119.750.400 | 0,0550125743 | 0,0000035722 | 0,0000001965 |
| 5-3-1-1-1-1 | 19.958.400 | 0,0091687624 | 0,0000035722 | 0,0000000328 |
| 5-2-2-2-1- | 59.875.200 | 0,0275062872 | 0,0000035722 | 0,0000000983 |
| 5-2-2-1-1-1 | 59.875.200 | 0,0275062872 | 0,0000035722 | 0,0000000983 |
| 4-4-4-0-0-0 | 693.000 | 0,0003183598 | 0,0000005954 | 0,0000000002 |
| 4-4-3-1-0-0 | 24.948.000 | 0,0114609530 | 0,0000005954 | 0,0000000068 |
| 4-4-2-2-0-0 | 18.711.000 | 0,0085957147 | 0,0000005954 | 0,0000000051 |
| 4-4-2-1-1-0 | 74.844.000 | 0,0343828589 | 0,0000005954 | 0,0000000205 |
| 4-4-1-1-1-1 | 12.474.000 | 0,0057304765 | 0,0000005954 | 0,0000000034 |
| 4-3-3-2-0-0 | 49.896.000 | 0,0229219060 | 0,0000005954 | 0,0000000136 |
| 4-3-3-1-1-0 | 99.792.000 | 0,0458438119 | 0,0000005954 | 0,0000000273 |
| 4-3-2-2-1-0 | 299.376.000 | 0,1375314358 | 0,0000005954 | 0,0000000819 |
| 4-3-2-1-1-1 | 199.584.000 | 0,0916876238 | 0,0000005954 | 0,0000000546 |
| 4-2-2-2-2-0 | 37.422.000 | 0,0171914295 | 0,0000005954 | 0,0000000102 |
| 4-2-2-2-1-1 | 149.688.000 | 0,0687657179 | 0,0000005954 | 0,0000000409 |
| 3-3-3-3-0-0 | 5.544.000 | 0,0025468784 | 0,0000000992 | 0,0000000003 |
| 3-3-3-2-1-0 | 133.056.000 | 0,0611250826 | 0,0000000992 | 0,0000000061 |
| 3-3-3-1-1-1 | 44.352.000 | 0,0203750275 | 0,0000000992 | 0,0000000020 |
| 3-3-2-2-2-0 | 99.792.000 | 0,0458438119 | 0,0000000992 | 0,0000000045 |
| 3-3-2-2-1-1 | 299.376.000 | 0,1375314358 | 0,0000000992 | 0,0000000136 |
| 3-2-2-2-2-1 | 149.688.000 | 0,0687657179 | 0,0000000992 | 0,0000000068 |
| 2-2-2-2-2-2 | 7.484.400 | 0,0034382859 | 0,0000000165 | 0,0000000001 |
| Total | 2.176.782.336 | 1,0000000000 | 0,0000037953 |
Clique no botão abaixo para ver a resposta.
Aqui está minha solução . (PDF)
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Suponha que um dado honesto de seis lados seja lançado até que apareça um 1, 2, 3 ou 6. Se um 1, 2 ou 3 for o primeiro desses números a aparecer, você não ganha nada. Se um 6 for o primeiro desses números a aparecer, você ganha $1 a cada lançamento do dado. Qual é o ganho médio neste jogo?
Clique no botão abaixo para ver algumas fórmulas de séries infinitas que podem ser úteis.
Dica 1: Soma de n i = 1 / (1-n) para i = 0 até ∞
Dica 2: Soma de i = 0 a ∞ de i × n i = n / (1-n) 2
Clique no botão abaixo para ver a resposta.
Clique no botão abaixo para ver a solução.
Suponha que um dado honesto de seis lados seja lançado até que apareça um 1, 2, 3 ou 6. Se um 1, 2 ou 3 for o primeiro desses números a aparecer, você não ganha nada. Se um 6 for o primeiro desses números a aparecer, você ganha $1 a cada lançamento do dado. Qual é o ganho médio neste jogo?
Dica 1: Soma de n i = 1 / (1-n) para i = 0 até ∞
Dica 2: Soma de i = 0 a ∞ de i × n i = n / (1-n) 2
O ganho esperado pode ser expresso como a soma, para i = 0 até ∞, de (1 + i) * (1/3) i * (1/6). =
(1/6) * soma para i = 0 até ∞ de (1/3) i + (1/6) * soma para i = 0 até ∞ de (i * (1/3) i ).
Vamos avaliar cada um deles individualmente.
soma para i = 0 até ∞ de (1/3) i =
1 / (1 - (1/3)) =
1 / (2/3) =
3/2
Soma de i = 0 a ∞ de (i * (1/3) i ) =
(1/3) / (1 - (1/3)) 2 =
(1/3) / (4/9) =
(1/3) * (9/4) =
3/4
Em resumo, a resposta é
(1/6) * (3/2) + (1/6)*(3/4) =
(1/4) + (1/8) =
3/8
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Embora isso pudesse ser resolvido com uma longa e tediosa cadeia de Markov, eu prefiro uma solução integral. Explico como usar esse método nas minhas páginas sobre Fire Bet e Bonus Craps .
Imagine que, em vez de os eventos significativos serem determinados pelo lançamento de um dado, um de cada vez, considere-os como um instante no tempo. Suponha que o intervalo de tempo entre os eventos tenha uma propriedade de ausência de memória, com um tempo médio entre eventos de uma unidade de tempo. Em outras palavras, o intervalo de tempo entre os eventos segue uma distribuição exponencial com média de 1. Isso não será relevante para fins de resolução da aposta, pois os eventos ainda ocorrerão um de cada vez.
De acordo com a distribuição de Poisson, a probabilidade de que qualquer face do dado tenha sido lançada zero vezes em x unidades de tempo é exp(-x/6)*(x/6) = 0 / 0! = exp(-x/6). A distribuição de Poisson também afirma que a probabilidade de que qualquer face seja lançada exatamente uma vez é exp(-x/6)*(x/6) = 1 / 1! = exp(-x/6) * (x/6). Assim, a probabilidade de que qualquer face tenha sido lançada duas ou mais vezes em x unidades de tempo é 1 - exp(-x/6)*(1 + (x/6)). A probabilidade de que todas as seis faces tenham sido lançadas pelo menos duas vezes é (1 - exp(-x/6)*(1 + (x/6))) = 6. A probabilidade de que pelo menos uma face não tenha sido lançada pelo menos duas vezes é igual a:
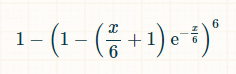
Precisamos integrar isso ao longo de todo o período para descobrir quanto tempo, em média, transcorrerá sem que o objetivo desejado seja alcançado.
Felizmente, podemos usar uma calculadora de integrais neste ponto. Para a calculadora indicada, insira 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = aproximadamente 24,1338692 na caixa de texto após "Calcular a integral de" e, em personalizado, defina o limite de integração de 0 a ∞.
A resposta é 390968681 / 16200000 = aproximadamente 24,13386919753086
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Você começa com um dado honesto de 6 lados e o lança seis vezes, registrando os resultados de cada lançamento. Em seguida, você escreve esses números nas seis faces de outro dado honesto, sem rótulos. Por exemplo, se seus seis lançamentos foram 3, 5, 3, 6, 1 e 2, então seu segundo dado não teria um 4; em vez disso, teria dois 3s.
Em seguida, você lança este segundo dado seis vezes. Você pega esses seis números e os escreve nas faces de um terceiro dado honesto, e continua esse processo de gerar um novo dado a partir do anterior.
Eventualmente, você terá um dado com o mesmo número em todas as seis faces. Qual é o número médio de transições de um dado para outro (ou o total de lançamentos dividido por 6) para chegar a esse estado?
Para evitar confusão, vamos rotular o dado inicial com letras em vez de números. Vamos rotular cada estado possível do dado com letras. Por exemplo, AAABBC significaria três de uma letra, duas de outra e uma de uma terceira. O estado inicial seria obviamente ABCDEF.
Seja E(ABCDEF) o número esperado de lançamentos a partir do estado ABCDEF.
E (ABCDEF) = 1 + [180 × E (AAAAAB) + 450 × E (AAAABB) + 300 × E (AAABBB) + 1800 × E (AAAABC) + 7200 × E (AAABBC) + 1800 × E (AABBCC) + 7200 × E (AAABCD) + 16200 × E (AABBCD) + 10800 × E(AABCDE) + 720 × E(ABCDEF)]/46656Com base no número de combinações de transição entre estados, a seguinte matriz de transição mostra quantas maneiras existem de ir de cada estado inicial (coluna da esquerda) para cada novo estado. Aliás, levou algumas horas para construí-la corretamente.
Matriz de Transição A
| Estado Antes | AAAAAA | AAAAAB | AAAABB | AAABBB | AAAABC | AAABBC | AABBCC | AAABCD | AABBCD | AABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|---|
| AAAAAB | 15.626 | 18.780 | 9.750 | 2.500 | - | - | - | - | - | - | - |
| AAAABB | 4.160 | 13.056 | 19.200 | 10.240 | - | - | - | - | - | - | - |
| AAABBB | 1.458 | 8.748 | 21.870 | 14.580 | - | - | - | - | - | - | - |
| AAAABC | 4.098 | 12.348 | 8.190 | 2.580 | 7.920 | 10.080 | 1.440 | - | - | - | - |
| AAABBC | 794 | 5.172 | 8.670 | 5.020 | 6.480 | 17.280 | 3.240 | - | - | - | - |
| AABBCC | 192 | 2.304 | 5.760 | 3.840 | 5.760 | 23.040 | 5.760 | - | - | - | - |
| AAABCD | 732 | 4.464 | 4.140 | 1.680 | 7.920 | 14.400 | 2.520 | 4.320 | 6.480 | - | - |
| AABBCD | 130 | 1.596 | 3.150 | 1.940 | 5.280 | 16.800 | 3.600 | 4.800 | 9.360 | - | - |
| AABCDE | 68 | 888 | 1.380 | 760 | 3.960 | 11.520 | 2.520 | 7.200 | 14.040 | 4.320 | - |
| ABCDEF | 6 | 180 | 450 | 300 | 1.800 | 7.200 | 1.800 | 7.200 | 16.200 | 10.800 | 720 |
Não vou me alongar em álgebra matricial, exceto para dizer que, digamos, a matriz B seja a seguinte:
Matriz B
| Estado Antes | AAAAAB | AAAABB | AAABBB | AAAABC | AAABBC | AABBCC | AAABCD | AABBCD | AABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|
| AAAAAB | -27876 | 9750 | 2500 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABB | 13056 | -27456 | 10240 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAABBB | 8748 | 21870 | -32076 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABC | 12348 | 8190 | 2580 | -38736 | 10080 | 1440 | 0 | 0 | 0 | -46656 |
| AAABBC | 5172 | 8670 | 5020 | 6480 | -29376 | 3240 | 0 | 0 | 0 | -46656 |
| AABBCC | 2304 | 5760 | 3840 | 5760 | 23040 | -40896 | 0 | 0 | 0 | -46656 |
| AAABCD | 4464 | 4140 | 1680 | 7920 | 14400 | 2520 | -42336 | 6480 | 0 | -46656 |
| AABBCD | 1596 | 3150 | 1940 | 5280 | 16800 | 3600 | 4800 | -37296 | 0 | -46656 |
| AABCDE | 888 | 1380 | 760 | 3960 | 11520 | 2520 | 7200 | 14040 | -42336 | -46656 |
| ABCDEF | 180 | 450 | 300 | 1800 | 7200 | 1800 | 7200 | 16200 | 10800 | -46656 |
A resposta é o determinante da matriz B em relação ao determinante da matriz A:
Determ(A) = 1.461.067.501.120.670.000.000.000.000.000.000.000.000.000.000
Determ(B) = 14.108.055.348.203.100.000.000.000.000.000.000.000.000.000.000
Determ(B) / Determ(A) = aproximadamente 9,65599148388557
A resposta pode ser aproximada como expressa por 1 - (prob(nenhum 1) + prob(nenhum 2) + ... + prob(nenhum 6)) = 1 - 6*(5/6)^20 = aproximadamente 0,84349568.
No entanto, isso subtrairia duas vezes as situações em que dois lados diferentes nunca foram lançados. Existem combin(6,2) = 15 maneiras de escolher dois lados dentre seis. A probabilidade de que quaisquer dois lados dados nunca sejam lançados é (4/6)^20. Precisamos adicionar esses valores à probabilidade, porque eles foram subtraídos duas vezes na etapa anterior. Então, agora temos 1 - 6*(5/6)^20 + 15*(4/6)^20 = aproximadamente 0,84800661.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
No entanto, se qualquer grupo de três lados que nunca foram rolados tivesse sido triplamente subtraído na primeira etapa e triplamente adicionado na segunda etapa, precisamos subtraí-los novamente como um estado em que nem todos os seis lados foram rolados. Existem combin(6,3) = 20 maneiras de escolher três lados dentre os seis. A probabilidade de que quaisquer três lados específicos nunca sejam rolados é (3/6)^20. Portanto, agora temos 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 = aproximadamente 0,847987537.
No entanto, se qualquer grupo de quatro lados que nunca tivesse sido lançado tivesse sido quadruplicado na primeira etapa, quadruplicado na segunda etapa e quadruplicado na terceira etapa, precisamos adicioná-los novamente, porque cada estado desse tipo já foi subtraído duas vezes. Existem combin(6,4) = 15 maneiras de escolher quatro lados dentre seis. A probabilidade de que quaisquer quatro lados específicos nunca sejam lançados é (2/6)^20. Portanto, agora temos 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 = aproximadamente 0,84798754089.
No entanto, se todos os 20 lançamentos fossem iguais, esta situação teria sido subtraída cinco vezes na primeira etapa, somada cinco vezes na primeira etapa, subtraída cinco vezes na terceira etapa e somada cinco vezes na quarta etapa. Precisamos subtraí-las novamente. Então, agora temos 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 - 6*(1/6)^20 = aproximadamente 0,84798754089.
Portanto, a resposta é 1-6*(5/6)^20+COMBIN(6,4)*(4/6)^20-COMBIN(6,3)*(3/6)^20+COMBIN(6,2)*(2/6)^20-6*(1/6)^20 = aproximadamente 0,84798754089.
Você tem dois dados. Você pode numerar cada face de ambos os dados como quiser, contanto que cada face seja um número inteiro maior ou igual a um. Você pode repetir o mesmo número no mesmo dado e aumentar o número o quanto quiser. Além de criar dados padrão, como você pode numerá-los de forma que a probabilidade de qualquer total seja a mesma que a de dados padrão?
Dado 1 = 1,2,2,3,3,4.
Dado 2 = 1,3,4,5,6,8.
Receio que a minha solução para este problema tenha sido, em grande parte, tentativa e erro.
Uma cadeia de Markov poderia ser usada para responder a essa pergunta, mas eu prefiro o cálculo diferencial e integral. A questão principal é que a resposta é a mesma se o intervalo de tempo entre os lançamentos seguir uma distribuição exponencial com média igual a um. Dito isso, a resposta pode ser expressa como a integral de 0 ao infinito de:
1-(1-exp(-x/36))^2*(1-exp(-x/18))^2*(1-exp(-x/12))^2*(1-exp(-x/9))^2*(1-exp(-5*x/36))^2*(1-exp(-x/6))
Você pode resolver facilmente essas integrais com uma calculadora de integrais .
Você também pode resolver qualquer problema desse tipo com a minha Calculadora de Ensaios Esperados .
Drop Dead é um jogo jogado com cinco dados padrão. Você começa sua vez rolando os cinco dados. Se nenhum deles for 2 ou 5, você soma os dados, adiciona a soma à sua pontuação e rola novamente. Se você rolar algum 2 ou 5, sua pontuação para a rolagem é zero. Todos os dados que mostrarem 2 ou 5 são considerados mortos e descartados. Você então rola novamente com os dados restantes. O jogo continua com você marcando pontos ou descartando dados. Sua vez termina quando todos os seus dados forem eliminados, momento em que se diz que você "morreu". Todas as suas pontuações são somadas para obter sua pontuação final. Quem tiver a maior pontuação vence.
Qual é a sua expectativa de pontuação para este jogo?
Vamos começar com o cenário em que resta apenas um dado e prosseguir para trás.
Seja a variável a quantidade de pontos adicionais esperados com um dado restante.
A média dos resultados que não são 2 ou 5 é (1+3+4+6)/4 = 7/2.
a = (2/3)×(a + 7/2).
a/3 = 7/3.
a = 7.
Em seguida, vamos calcular b, a pontuação esperada com dois dados restantes.
b = (2/3) 2 ×(b + 2 × (7/2)) + 2×(2/3)×(1/3)×a.
b = 11,2.
Em seguida, vamos calcular c, a pontuação esperada com três dados restantes.
c = (2/3) 3 ×(c + 3× (7/2)) + 3×(2/3) 2 ×(1/3)×b + 3×(2/3)×(1/3) 2 ×b.
c = 1302/95 = 13,705263.
Em seguida, vamos calcular d, a pontuação esperada com quatro dados restantes.
d = (2/3) 4 ×(d + 4× (7/2)) + 4×(2/3) 3 ×(1/3)×c + 6×(2/3) 2 ×(1/3) 2 ×b + 4×(2/3)×(1/3) 3 ×a.
d = 3752/247 = 15,190283.
Por fim, vamos calcular e, a pontuação esperada com cinco dados restantes.
e = (2/3) 5 ×(e + 5×(7/2)) + 5×(2/3) 4 ×(1/3)×d + 10×(2/3) 3 ×(1/3) 2 ×c + 10×(2/3) 2 ×(1/3) 3 ×b + 5×(2/3)×(1/3) 4 ×a.
e = 16,064662.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Lance dois dados, um vermelho e um azul, repetidamente. Anote a soma dos lançamentos para cada dado. Qual é o número esperado de lançamentos até que os dois totais acumulados sejam iguais?
É difícil explicar por que a resposta é infinito. Para tornar as coisas ainda mais confusas e paradoxais, a probabilidade de os totais serem iguais em algum momento é 1.
A tabela a seguir mostra a probabilidade de os totais serem iguais pela primeira vez após 1 a 16 lançamentos.
Probabilidade de totais iguais para a primeira vez
| Rolls | Probabilidade |
|---|---|
| 1 | 0,166667 |
| 2 | 0,112654 |
| 3 | 0,092850 |
| 4 | 0,080944 |
| 5 | 0,072693 |
| 6 | 0,066539 |
| 7 | 0,061722 |
| 8 | 0,057819 |
| 9 | 0,054573 |
| 10 | 0,051819 |
| 11 | 0,049443 |
| 12 | 0,047367 |
| 13 | 0,045532 |
| 14 | 0,043895 |
| 15 | 0,042423 |
| 16 | 0,041089 |
O Excel mostra que um ajuste muito próximo a esta curva é y = 0,1784*x-1,011, onde x = número de lançamentos e y = probabilidade.
A soma dessa série infinita é infinita.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Cinco dados vermelhos e cinco dados azuis são lançados. Qual é a probabilidade de que o resultado do lançamento seja o mesmo para ambos os dados, independentemente da ordem? Por exemplo, se ambos os lançamentos forem 1-2-3-3-6.
A tabela a seguir mostra os resultados para qualquer tipo de rolo:
- O número de maneiras diferentes de se obter essa combinação. Por exemplo, para um full house, existem seis combinações para a trinca e cinco para o par, totalizando 30 full houses diferentes.
- O número de pedidos. Por exemplo, para uma trinca, existem combin(5,3)=10 maneiras de escolher três dos cinco dados para a trinca. Os outros dois devem ter o par.
- O número de maneiras de se obter uma determinada mão de cartas. Este é o produto das duas primeiras colunas. Por exemplo, existem 30 * 10 = 300 maneiras de se obter um full house.
- A probabilidade da mão. Por exemplo, para um full house a probabilidade é 300/6 5 = 0,038580.
- A probabilidade de ambos os lançamentos serem iguais e da mão dada. Esta é a probabilidade da quarta coluna ao quadrado dividida pela segunda coluna. Por exemplo, a probabilidade de dois lançamentos serem ambos um full house é 0,038580² . No entanto, a probabilidade de serem o mesmo full house é 1/30. Portanto, a probabilidade de ambos os lançamentos serem o mesmo full house é 0,038580² / 30 = 0,00004961.
A célula inferior direita mostra que a probabilidade total de ambos os lançamentos serem iguais é 0,00635324.
Rolo de correspondência
| Tipo de Roll | Diferente Tipos | Pedidos | Total Combinações | Probabilidade Um rolo | Probabilidade Dois rolos | |
|---|---|---|---|---|---|---|
| Cinco de um tipo | 6 | 1 | 6 | 0,00077160 | 0,00000010 | |
| Quatro de um mesmo tipo | 30 | 5 | 150 | 0,01929012 | 0,00001240 | |
| Casa cheia | 30 | 10 | 300 | 0,03858025 | 0,00004961 | |
| Três de um tipo | 60 | 20 | 1.200 | 0,15432099 | 0,00039692 | |
| Dois pares | 60 | 30 | 1.800 | 0,23148148 | 0,00089306 | |
| Par | 60 | 60 | 3.600 | 0,46296296 | 0,00357225 | |
| Cinco indivíduos isolados | 6 | 120 | 720 | 0,09259259 | 0,00142890 | |
| Total | 7.776 | 1.00000000 | 0,00635324 |
Um dado de seis lados é lançado até que um dos seguintes eventos ocorra:
A) Qualquer um dos lados já apareceu seis vezes.
B) Todos os lados já apareceram pelo menos uma vez.
Qual é a probabilidade de o evento A ocorrer primeiro?
Para responder a esta pergunta como eu fiz, usando cálculo, recomendo uma calculadora de integrais como a do site integral-calculator.com/ .
Aqui está minha solução (PDF).
Este problema é apresentado (com palavras ligeiramente diferentes) e discutido no meu fórum no Wizard of Vegas .
Você deseja jogar um jogo que requer um dado comum de seis lados. Infelizmente, você perdeu o dado. No entanto, você tem quatro fichas, que pode marcar como quiser. O jogador deve escolher duas fichas aleatoriamente dentre as quatro, sem reposição, e somar os valores das duas fichas.
Como numerar as cartas de forma que a soma de duas cartas diferentes represente o resultado do lançamento de um dado?
Numere-os de 0 a 4.
Existem seis maneiras de comprar duas cartas dentre quatro, conforme descrito a seguir.
- 0+1 = 1
- 0+2 = 2
- 1+2 = 3
- 0+4 = 4
- 1 + 4 = 5
- 2+4 = 6
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Um dado de seis lados é lançado repetidamente até que a soma dos lançamentos seja igual ou superior a 13. Quais são a média, a mediana e a moda do total final?
Mediana = 14
Modo = 13
Para isso, precisei usar uma Cadeia de Markov. A tabela a seguir mostra a probabilidade de cada total final de acordo com a soma acumulada na coluna da esquerda. Comece com os casos óbvios para totais de 13 a 18. Em seguida, para somas acumuladas de 0 a 12, calcule a média das seis células abaixo.
As probabilidades para o estado inicial podem ser encontradas na primeira linha para uma soma de 0.
Cadeia de Markov
| Soma dos Rolos | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|
| 0 | 0,279263 | 0,236996 | 0,192313 | 0,145585 | 0,097371 | 0,048472 |
| 1 | 0,290830 | 0,230791 | 0,188524 | 0,143842 | 0,097114 | 0,048899 |
| 2 | 0,293393 | 0,241931 | 0,181893 | 0,139625 | 0,094943 | 0,048215 |
| 3 | 0,289288 | 0,245178 | 0,193717 | 0,133678 | 0,091410 | 0,046728 |
| 4 | 0,280369 | 0,242560 | 0,198450 | 0,146988 | 0,086950 | 0,044682 |
| 5 | 0,268094 | 0,235687 | 0,197878 | 0,153768 | 0,102306 | 0,042267 |
| 6 | 0,253604 | 0,225827 | 0,193419 | 0,155611 | 0,111500 | 0,060039 |
| 7 | 0,360232 | 0,193566 | 0,165788 | 0,133380 | 0,095572 | 0,051462 |
| 8 | 0,308771 | 0,308771 | 0,142104 | 0,114326 | 0,081919 | 0,044110 |
| 9 | 0,264660 | 0,264660 | 0,264660 | 0,097994 | 0,070216 | 0,037809 |
| 10 | 0,226852 | 0,226852 | 0,226852 | 0,226852 | 0,060185 | 0,032407 |
| 11 | 0,194444 | 0,194444 | 0,194444 | 0,194444 | 0,194444 | 0,027778 |
| 12 | 0,166667 | 0,166667 | 0,166667 | 0,166667 | 0,166667 | 0,166667 |
| 13 | 1.000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 |
| 14 | 0,000000 | 1.000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 |
| 15 | 0,000000 | 0,000000 | 1.000000 | 0,000000 | 0,000000 | 0,000000 |
| 16 | 0,000000 | 0,000000 | 0,000000 | 1.000000 | 0,000000 | 0,000000 |
| 17 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 1.000000 | 0,000000 |
| 18 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 1.000000 |
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Como você sabe, a aposta "All" no craps ganha se todos os totais de 2 a 12, exceto 7, forem lançados antes de um 7. Quantas rodadas, em média, são necessárias para ganhar essa aposta, quando ela é ganha?
Aqui está minha solução (PDF).
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Vejo que alguém afirma ter testemunhado 18 jovens consecutivos (total de 11) em uma mesa de dados. Em média, quantas rodadas seriam necessárias para observar isso?
Aqui está minha solução (PDF).
Um par de dados honestos de seis lados é lançado repetidamente até que um dos dois eventos a seguir ocorra:
A) Um total de 12 foi obtido ao rolar os dados.
B) O resultado de um total de 7 é obtido duas vezes consecutivas.
Qual das duas opções tem maior probabilidade de acontecer primeiro?
[spoiler=Solução]
Deixar:
- p = Probabilidade de o 12 ser rolado primeiro a partir do estado inicial ou sempre que a rolagem anterior não foi um 7.
- q = Probabilidade de sair o 12 primeiro quando o resultado do lançamento anterior foi 7.
Isso é o que se conhece como um problema de Cadeia de Markov.
Antes de prosseguirmos, lembre-se de que a probabilidade de rolar um total de 7 é 1/6 e a de um 12 é 1/36.
Podemos definir p e q em função um do outro, da seguinte forma:
- (1) p = (1/36) + (6/36)q + (29/36)p
- (2) q = (1/36) + (29/36)p
Vamos multiplicar a equação (1) por 36:
36p = 1 + 6q + 29p
(3) 7p = 1 + 6q
Vamos substituir o valor de q em (2) em (3):
7p = 1 + 6*((1/36) + (29/36)p)
7p = 1 + (1/6) + (29/6)p
42p = 6 + 1 + 29p
13p = 7
q = 7/13
Assim, a probabilidade de tirar o 12 primeiro é 7/13 ≈ 53,85%.
A probabilidade de rolar dois 7 consecutivos primeiro é, portanto, de 46,15%.
Assim, é mais provável que o total de 12 seja obtido primeiro.