Probabilidade - Perguntas gerais
Você está dizendo que, a longo prazo, você perderá em todos os jogos de cassino, não importa o que faça?
Com exceção de raras oportunidades de expectativa positiva no blackjack e no vídeo pôquer, sim, é isso que estou dizendo.
Como posso converter suas probabilidades para o formato x para y?
Dizer que a probabilidade de algo acontecer é de x para y significa que o evento em questão ocorrerá x vezes para cada y vezes que não ocorrer. Para fazer a conversão, seja p a probabilidade de algum evento. A probabilidade também pode ser expressa como (1/p)⁻¹ para 1. Vejamos um exemplo. A probabilidade de tirar um full house no jogo de cinco cartas é 0,00144058. Isso também pode ser representado como 693,165 para 1.
Recentemente, estava olhando um bolão de futebol que estava rolando. Era um daqueles com uma grade de 100 quadrados, onde os números de 0 a 9 corriam nos eixos X e Y e correspondiam ao último gol do placar. Não sou fã de futebol e não apostei nesse bolão, mas como sou apostador, não acho que seja uma aposta muito boa.
Estou partindo do princípio de que você sabe a que tipo de bolão me refiro. Cada caixa custa US$ 5 e os prêmios são pagos a cada trimestre. Se a sua caixa for vencedora, você ganha US$ 125, e é possível ganhar nos 4 trimestres se os últimos números permanecerem os mesmos, ganhando US$ 500, o que representa um pagamento de 100 para 1.
A pessoa que me ofereceu a aposta estava tentando me convencer de que as chances de ganhar os 500 dólares são de 100 para 1. Discordo. Primeiro, a combinação com 0 + 7 tem uma chance muito maior de ganhar do que a combinação com 2 + 9. No entanto, a probabilidade de 0 + 7 permanecerem como os dois últimos números durante todo o jogo deve ser alta. Se as combinações forem escolhidas aleatoriamente, você poderia me dizer qual a probabilidade aproximada de ganhar o prêmio de 500 dólares?
Supondo que as células na grade sejam escolhidas aleatoriamente, a probabilidade de ganhar qualquer trimestre seria de 1/100. Supondo que cada trimestre fosse um evento independente, o que não é o caso, a probabilidade de ganhar todos os quatro trimestres seria de (1/100) ⁴ = 1 em 100 milhões.
Gostaria muito de saber como interpretar probabilidades como 12 para 1 ou 3 para 2. Qual delas indica as melhores chances de ganhar? 12 para 1 ou 3 para 2?
Eu não gosto de usar probabilidades dessa forma, mas elas geralmente são usadas com essa sintaxe: "As chances de não conseguir um royal flush são de 649.739 para 1". Isso significa que existem 649.739 maneiras de você não conseguir um royal flush e apenas 1 maneira de conseguir. Nos seus exemplos, 12 para 1 é uma probabilidade de 1/13, ou 7,69%, e 3 para 2 é 2/5, ou 40,00%, então a probabilidade de 3 para 2 é a melhor.
Em um artigo do St. Louis Post-Dispatch, o repórter afirma: "Uma enchente que ocorre a cada 500 anos é aquela que tem 1 chance em 500 de acontecer em qualquer ano. Ou seja, 1 chance em 10 de acontecer ao longo de 50 anos, ou 1 chance em 5 de acontecer ao longo de um século." Depois de ler todas as suas páginas sobre jogos de azar, acredito que essa não seja a maneira correta de colocar a questão, certo? Extrapolando essa afirmação, significaria que há uma chance de 1 em 1 de que uma enchente ocorra a cada 500 anos, e isso não pode estar correto.
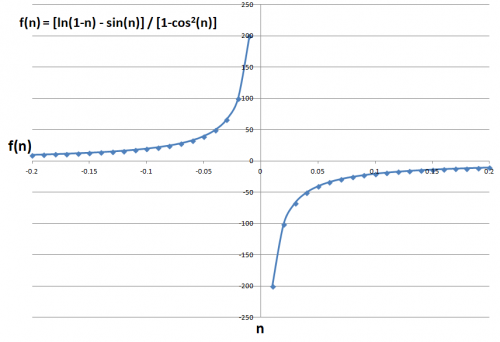
Você tem razão, aquele artigo está incorreto. A probabilidade de uma inundação que ocorre a cada 500 anos em um período de x anos é 1 - e^ (-x/500) . Portanto, a probabilidade de ocorrer pelo menos uma inundação que ocorre a cada 500 anos em 50 anos é de 9,52% e em 100 anos é de 18,13%.
Se eu determinar que a linha justa de um jogo é -160/+160 e encontrar uma linha irregular de -145, qual é o meu valor esperado (EV)? Qualquer fórmula que você possa fornecer para calcular meu EV (+/-) após a determinação da linha justa será muito apreciada.
Seja p a probabilidade de o favorito vencer. Se -160 for uma linha justa, então:
100*p - 160*(1-p) = 0
260p = 160
p = 160/260 = 8/13 = 61,54%.
Assim, o retorno esperado de uma aposta de $145 em uma linha de -145 seria (8/13)*100 + (5/13)*-145 = 75/13 = $5,77. Portanto, a vantagem do jogador seria de $5,77/$145 = 3,98%.
Vamos definir t como a linha de dinheiro verdadeira, sem vantagem da casa, e a como a linha de dinheiro real. A seguir, as fórmulas para o retorno esperado do jogador:
A é negativo, t é negativo: (100*(ta) / (a*(100-t))
A é positivo, t é positivo: (at)/(100+t)
A é positivo, t é negativo: (a*t + 10000)/((t-100)*100)
Portanto, no seu caso, o retorno esperado é 100*(-160 -(-145))/(-145*(100-(-160))) = 3,98%.
O que você acha da afirmação abaixo, de que Deus é um democrata, como evidenciado pelo fato de que todos os condados que votaram em Gore em 2000 foram poupados pelos três furacões que atingiram a Flórida recentemente?
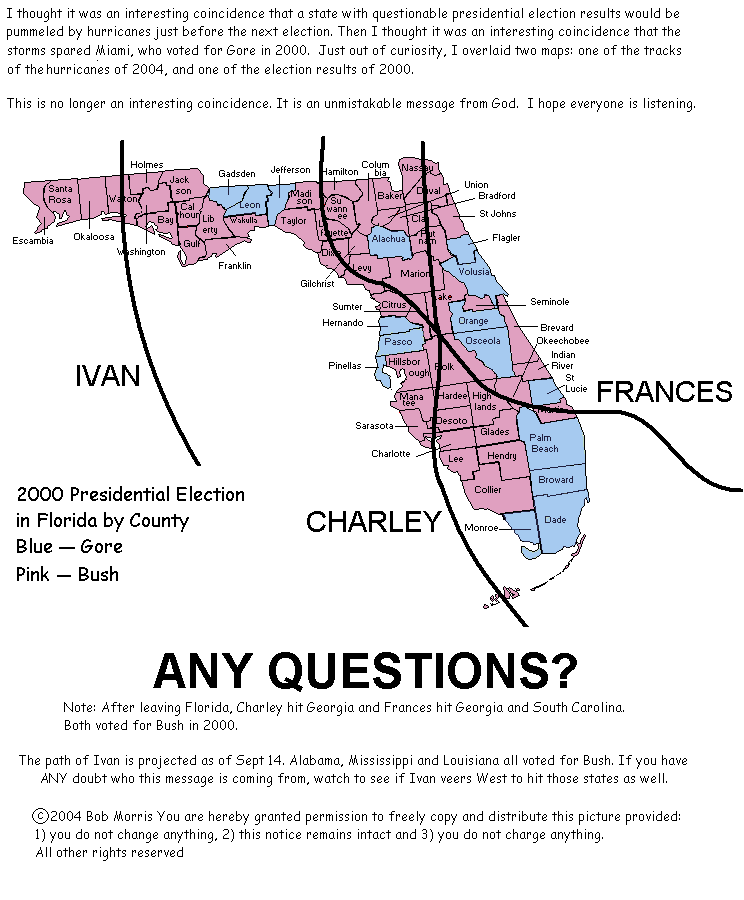
Primeiramente, estou publicando isso porque o autor autorizou, conforme indicado no final. Este é um bom exemplo de que correlação não implica necessariamente causalidade. É fácil olhar para o passado e encontrar muitas coincidências. Para fundamentar qualquer argumento, uma hipótese deve ser formulada antes de qualquer coleta de evidências.
Atualização (13 de novembro de 2004): Outro leitor apontou que este mapa começou como uma piada, mas se transformou em uma lenda urbana . Como este link demonstra, as trajetórias dos furacões no gráfico simplesmente não eram precisas e os furacões reais atingiram muitos condados de Gore. Isso só mostra que não se deve acreditar em tudo que se lê, especialmente na internet.
Achei que você poderia achar isso interessante. No Bodog, eles oferecem a seguinte aposta: "O segundo filho de Britney Spears e Kevin Federline será menino ou menina?" As probabilidades para menino são de +105 e para menina, de -145. Pelo que sei, a proporção é de 1:1 desde o início da humanidade. Gostaria de saber quem está apostando no lado de -145. Adoro o site, visito sempre e clico nos patrocinadores como forma de agradecimento.
Obrigado pelas palavras gentis. Para ser honesto, ninguém se importa muito com taxas de cliques hoje em dia. Então, não se sinta obrigado a clicar nos banners se for apenas para exibição. Respondendo à sua pergunta, nos Estados Unidos, as probabilidades são muito próximas de 50,5% menino e 49,5% menina. Supondo que nenhuma outra informação seja conhecida pela comunidade de apostadores, a vantagem do jogador na aposta em menino seria de 0,505 * 1,05 - 0,495 = 3,53%. Pode ser que alguém com informações privilegiadas esteja apostando em menina. Outra teoria é que algumas pessoas acreditam erroneamente que é possível determinar o sexo do bebê pelo formato da barriga da mãe, e essas pessoas estão apostando em menina. Pessoalmente, vou deixar essa teoria de lado.
Neste vídeo do YouTube , Matt Damon diz que John McCain tem uma chance em três de não sobreviver ao seu primeiro mandato. Ele está certo?
Não. Usando esta tabela atuarial do CDC (Centros de Controle e Prevenção de Doenças), a probabilidade de um homem branco de 72 anos chegar aos 76 anos é de 85,63%. Isso equivale a cerca de 1 chance em 7 de morte. A taxa de sobrevivência pode ser encontrada dividindo-se a coorte de nascimento aos 76 anos (57.985) pela coorte de nascimento aos 72 anos (67.719), conforme a tabela para homens brancos na página 14. A tabela utilizada é chamada de "tabela de vida de período", que pressupõe que as taxas de mortalidade de 2003 não mudarão no futuro, e é o tipo de tabela atuarial mais comumente usado. Um perfeccionista poderia preferir usar uma tabela de vida de coorte de 1936, mas não creio que faria muita diferença.
P.S.: Depois de publicar esta resposta, recebi vários comentários dizendo que minha resposta não levou em consideração a situação de saúde individual de John McCain. O fato de ele ser um sobrevivente de câncer pesa contra ele. Por outro lado, ele tem acesso aos melhores cuidados médicos disponíveis, está obviamente em boa forma física e mental para um homem de 72 anos e tem uma longa expectativa de vida, como evidenciado pelo fato de sua mãe ainda estar viva. No entanto, eu nunca tive a intenção de levar essa informação em consideração. Foi Matt Damon quem citou as tabelas atuariais, e era a isso que eu me referia. O que estou dizendo é que, para um homem branco de 72 anos, a probabilidade média de sobreviver mais quatro anos é de 86%. Se fosse obrigado a escolher, eu diria que as chances de John McCain são ainda melhores.
Considerando a mesma quantidade de papel, qual copo comportaria mais água: um cilindro ou um cone? Suponha que o cilindro seja aberto em uma das extremidades e que as dimensões sejam ótimas em ambos os casos.
Consulte o problema número 210 no meu site complementar MathProblems.info para obter a resposta e a solução.
Você já ouviu a história da Princesa, a camela do zoológico Popcorn Park em Nova Jersey, que tem um histórico de 88 vitórias e 51 derrotas em apostas contra o spread na NFL? Quais são as chances disso?
Sem contar os empates, a probabilidade de acertar pelo menos 88 palpites em 139 tentativas é de 0,00107355, ou 1 em 931. Isso é bem decepcionante. Tenho certeza de que existem outros 930 animais por aí que se saíram pior e sobre os quais ninguém escreve. Para mais informações sobre a Princesa, leia o artigo " Camelo de Nova Jersey prevê vitória dos Giants sobre os Patriots" no ESPN.com.
No programa Chelsea Lately de 8 de maio de 2012, Chelsea disse que os ruivos estão em extinção porque não se reproduzem entre si. Isso é verdade?
Espero que você esteja feliz; passei horas nisso.
Para responder à pergunta, é importante quantificar o comportamento sob a hipótese da ruiva Chelsea Handler. Aqui estão minhas suposições.
- Uma pessoa ruiva nunca irá acasalar com outra pessoa ruiva.
- A fêmea sempre escolherá o macho para acasalar.
- Todos irão acasalar e cada acasalamento produzirá o mesmo número de filhos.
- As fêmeas ruivas terão prioridade na escolha do parceiro, selecionando-o aleatoriamente entre os que não são ruivos.
- As mulheres portadoras (com um gene para cabelo ruivo) escolherão um parceiro aleatoriamente entre os homens que sobrarem das ruivas.
- As mulheres negativas (que não possuem o gene do cabelo ruivo) escolherão aleatoriamente entre os homens que sobrarem, tanto das ruivas quanto das portadoras.
Começo com uma probabilidade de 4% para pessoas ruivas, de acordo com o site Today I Found It . Em seguida, parto do princípio de que, até então, não havia preconceito contra ruivos.
Partindo do pressuposto que o preconceito contra ruivos comece na próxima geração e continue, qual será a tendência da população total em relação ao cabelo ruivo? Após muito trabalho em uma planilha, que não vou detalhar aqui, apresentamos as oito primeiras gerações, a partir desta.
Proporção de Cabelo Ruivo
| Geração | Proporção |
|---|---|
| 1 | 4,000000% |
| 2 | 3,888889% |
| 3 | 3,895219% |
| 4 | 3,894863% |
| 5 | 3,894883% |
| 6 | 3,894882% |
| 7 | 3,894882% |
| 8 | 3,894882% |
O que vemos é que, na terceira geração, a proporção da população com cabelos ruivos convergirá para 3,90%. Portanto, apesar do que Chelsea possa dizer, acho que os ruivos não têm nada com que se preocupar.
Essa questão foi levantada e discutida no meu fórum no Wizard of Vegas .
Segundo o CardPlayer.com , Amir Lehavot, um dos nove jogadores que chegaram à mesa final da World Series of Poker de 2013, está vendendo qualquer prêmio acima do mínimo de US$ 733.224 (equivalente ao nono lugar) por US$ 29.248 por cada 1% de participação. Será esse um preço justo?
Primeiro, vamos analisar as estruturas dos chips.
Pilhas de fichas da mesa final da WSOP de 2013
| Jogador | Batatas fritas |
|---|---|
| JC Tran | 38.000.000 |
| Amir Lehavot | 29.700.000 |
| Marc McLaughlin | 26.525.000 |
| Jay Farber | 25.975.000 |
| Ryan Riess | 25.875.000 |
| Sylvain Loosli | 19.600.000 |
| Michiel Brummelhuis | 11.275.000 |
| Mark Newhouse | 7.350.000 |
| David Benefield | 6.375.000 |
A tabela seguinte mostra a vitória para cada resultado final do torneio.
Prêmio em dinheiro da mesa final da WSOP de 2013
| Lugar | Ganhar |
|---|---|
| 1º | US$ 8.359.531 |
| 2º | $ 5.173.170 |
| 3º | $ 3.727.023 |
| 4º | $ 2.791.983 |
| 5º | $ 2.106.526 |
| 6º | US$ 1.600.792 |
| 7º | $ 1.225.224 |
| 8º | $ 944.593 |
| 9º | $ 733.224 |
Considerando que todos os jogadores tenham habilidades equivalentes, a probabilidade de vitória pode ser estimada pela porcentagem da pilha total de fichas. No entanto, a situação se complica a cada posição subsequente. Para ajudar a responder a essa pergunta, desenvolvi minha calculadora de torneios de poker .
Após inserir as informações acima, você verá que Amir tem um ganho esperado de US$ 3.658.046. Subtraindo o prêmio mínimo de US$ 733.224 para o 9º lugar, você obtém US$ 2.924.822 em ganhos esperados não garantidos. Cada participação de 1% tem um valor de US$ 29.248,22. Este é convenientemente o preço citado no artigo do cardplayer.com.
Aliás, Lehavot terminou em terceiro lugar, faturando US$ 3.727.023 em prêmios. Subtraindo os US$ 733.224 garantidos para o 9º lugar e dividindo por 100, cada ação de 1% rendeu US$ 29.938. O custo original por ação era de US$ 29.248, portanto, cada ação teria gerado um lucro de 2,36%.
Essa questão é discutida no meu fórum, Wizard of Vegas .
Para promoções de cassino que ainda usam bilhetes físicos em um tambor de verdade (não os eletrônicos), onde você imprime seus bilhetes no balcão de atendimento e os coloca no tambor, você dobra/amarra os bilhetes antes de colocá-los no tambor? Você acha que os bilhetes amassados têm mais chances de serem escolhidos?
Espero que você esteja feliz. Para responder a essa pergunta, comprei um rolo grande de bilhetes na Office Depot. Depois, coloquei 500 deles em um saco de papel, metade dobrado ao meio, em um ângulo de aproximadamente 90 graus, e a outra metade desdobrada. Em seguida, pedi a seis voluntários que sorteassem de 40 a 60 bilhetes cada, com reposição, enquanto eu anotava os resultados. Aqui estão os resultados.
Experimento de sorteio de bilhetes
| Assunto | Dobrado | Desdobrado | Total |
|---|---|---|---|
| 1 | 25 | 25 | 50 |
| 2 | 38 | 22 | 60 |
| 3 | 25 | 15 | 40 |
| 4 | 34 | 16 | 50 |
| 5 | 27 | 23 | 50 |
| 6 | 26 | 24 | 50 |
| Total | 175 | 125 | 300 |
Portanto, 58,3% dos bilhetes sorteados foram dobrados!
Se assumirmos que a desistência não teve efeito, então esses resultados estariam a 2,89 desvios padrão das expectativas. A probabilidade de obter essa quantidade de bilhetes desviados, ou mais, assumindo que a desistência não afetou as probabilidades, é de 0,19%, ou 1 em 514.
Eu acrescentaria que os participantes que sortearam os bilhetes às pressas tiveram muito mais probabilidade de tirar bilhetes dobrados. Já aqueles que dedicaram tempo a cada sorteio tiveram uma proporção de acerto próxima a 50/50.
Portanto, minha conclusão é definitivamente dobrá-las.
Para discutir este assunto, visite meu fórum no Wizard of Vegas .
Dois jogadores recebem um número aleatório no intervalo (0,1). O primeiro jogador decide se mantém sua carta ou descarta e compra um novo número. O segundo jogador faz o mesmo. O número mais alto vence. Qual é a estratégia ótima para cada jogador? Considerando a estratégia ótima, qual é a probabilidade de cada jogador vencer?
Ótima pergunta! Aqui está minha resposta e uma solução resumida. Veja também minha solução em formato PDF .
Imagine que lhe oferecessem a oportunidade de jogar um jogo de cara ou coroa. Se o primeiro lançamento der cara, você recebe $2 e o jogo termina. Caso contrário, você lança novamente. Se o segundo lançamento também der cara, você recebe $4. Se o segundo lançamento também der coroa, você continua lançando até sair cara. A cada lançamento, o prêmio dobra. Em outras palavras, você recebe 2^n, onde n é o número de lançamentos (incluindo o lançamento final em que deu cara). Quanto você pagaria para jogar este jogo? Ouvi dizer que a resposta matemática é uma quantia infinita de dinheiro, mas isso não faz sentido, porque você deve ganhar uma quantia finita de dinheiro em algum momento.
Isso é conhecido como o Paradoxo de São Petersburgo .
É verdade que o ganho esperado no jogo é infinito, enquanto a probabilidade de a moeda eventualmente cair em coroa, resultando em uma quantia finita de dinheiro, é de que isso aconteça. O cálculo do ganho esperado é:
Ganho esperado = pr(1 lançamento)×2 + pr(2 lançamentos)×4 + pr(3 lançamentos)×8 + pr(4 lançamentos)×16 + pr(5 lançamentos)×32 + pr(6 lançamentos)×64 + ... =
(1/2) 1 × 2 1 + (1/2) 2 × 2 2 + (1/2) 3 × 2 3 + (1/2) 4 × 2 4 + (1/2) 5 × 2 5 + (1/2) 6 × 2 6 + ...
= ((1/2)*(2/1)) 1 + ((1/2)*(2/1)) 2 + ((1/2)*(2/1)) 3 + ((1/2)*(2/1)) 4 + ((1/2)*(2/1)) 5 + ((1/2)*(2/1)) 6 + ...
= 1 1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + ...
= 1 + 1 + 1 + 1 + 1 + 1 + ... = ∞
O paradoxo reside no fato de que o jogador precisa ganhar uma quantia finita de dinheiro, mas o ganho esperado é infinito. Como isso é possível?
Esta provavelmente não é uma resposta muito satisfatória, mas existem muitos paradoxos quando se trata do infinito. Isso pode me render alguns e-mails raivosos, mas o que me permite dormir em paz, apesar de tais paradoxos do infinito, é que acredito que o infinito é um conceito matemático ou filosófico cuja existência no universo físico real ainda não foi comprovada. Esse conceito ou teoria do infinito carrega consigo paradoxos inerentes.
Para aqueles que discordam disso, por favor, me digam algo que comprovadamente possua quantidade ou medida infinita. Por favor, não digam que um buraco negro tem densidade infinita a menos que tenham evidências de seu tamanho.
Para responder à pergunta inicial sobre quanto se deve pagar para jogar este jogo, devemos ter em mente que a felicidade não é proporcional à quantidade de dinheiro. Pessoalmente, aprendi nas aulas de economia e acredito que a utilidade, ou felicidade, proveniente do dinheiro é proporcional ao logaritmo da quantia. Sob essa premissa, se você aumentar ou diminuir a riqueza de duas pessoas na mesma porcentagem, exceto partindo de uma riqueza inicial de zero, ambas experimentarão a mesma variação na felicidade. Por exemplo, se a riqueza de Jim aumentar repentinamente de US$ 1.000 para US$ 1.100 e a de John aumentar repentinamente de US$ 10.000.000 para US$ 11.000.000, ambos experimentarão o mesmo aumento na felicidade, porque em ambos os casos suas riquezas aumentaram em 10%. Supondo que a felicidade proveniente do dinheiro seja de fato proporcional ao logaritmo da quantia, a tabela a seguir mostra o valor máximo que alguém estaria disposto a pagar, de acordo com sua riqueza, para jogar.
Quantidade de indiferença para jogar
| Fortuna | Indiferença Quantia |
|---|---|
| $ 10 | $ 4,97 |
| $ 100 | $ 7,79 |
| $ 1.000 | $ 10,96 |
| $ 10.000 | $ 14,26 |
| $ 100.000 | $ 17,78 |
| $ 1.000.000 | $ 20,88 |
| $ 10.000.000 | $ 24,19 |
| US$ 100.000.000 | $ 27,51 |
| US$ 1.000.000.000 | $ 30,84 |
Como você pode ver, em condições realistas, o valor que você deveria pagar é muito menor que $∞. Por exemplo, se sua riqueza for de um milhão de dólares, você não deveria se importar em jogar por um custo de $20,88.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
A Loteria de Michigan oferece um jogo para três jogadores com as seguintes regras: Existe alguma vantagem posicional em jogar por último nesta partida? Qual é a estratégia ideal para cada jogador? Aqui está um vídeodo YouTube mostrando a partida.
Primeiro, não há vantagem posicional em ser o último a jogar. Como os jogadores ficam em uma cabine à prova de som enquanto os jogadores anteriores tocam, a ordem não importa.
Em segundo lugar, deve haver um equilíbrio de Nash no jogo, onde uma estratégia para manter uma pontuação de pelo menos x pontos seja superior a qualquer outra estratégia. A questão é encontrar x.
O que eu fiz foi me perguntar qual seria a estratégia se, em vez de um cartão numerado de 1 a 100, cada jogador recebesse um número aleatório distribuído uniformemente entre 0 e 1, e procurar o ponto x onde um lógico perfeito seria indiferente entre permanecer no mesmo lugar e trocar de carta. Com essa resposta, é fácil aplicá-la a uma distribuição discreta de 1 a 100.
Vou parar de falar por aqui e deixar que meus leitores apreciem o problema. Veja os links abaixo para a resposta e a solução.
Resposta para uma distribuição contínua de 0 a 1 .
Resposta para uma distribuição discreta de 1 a 100.
Para ver minha solução, clique aqui (PDF) .
Essa questão foi levantada e discutida no meu fórum no Wizard of Vegas .
Suponha que você tenha um baralho de dez cartas vermelhas e dez cartas pretas. Após um embaralhamento aleatório, você compra cartas sem reposição. Qual é a probabilidade de comprar todas as dez cartas pretas antes de comprar cinco cartas vermelhas?
Isso equivale a perguntar qual a probabilidade de que 14 cartas aleatórias contenham todas as 10 cartas pretas. Existem combin (10,4) = 210 maneiras de escolher 4 cartas vermelhas dentre as 10 do baralho. Obviamente, existe apenas uma maneira de escolher todas as dez cartas pretas. Existem combin(20,14) = 38.760 maneiras de escolher 14 cartas dentre as 20. Portanto, a resposta é 210/38.760 = 0,005418, ou 1 em 184,57.
Sei de uma promoção que paga um bônus após conseguir uma quadra em todas as 13 cartas do mesmo naipe. Quantas mãos são necessárias em média para isso?
Para responder à sua pergunta, vamos analisar o padrão ouro do vídeo pôquer, o 9-6 Jacks or Better .
O primeiro passo é modificar minha calculadora para incluir uma linha para cada uma das 13 quadras. Aqui está a tabela de retorno modificada:
Mesa de retorno modificada Jacks or Better
| Evento | Paga | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| Rubor Real | 800 | 493.512.264 | 0,000025 | 0,019807 |
| Straight flush | 50 | 2.178.883.296 | 0,000109 | 0,005465 |
| Quatro A | 25 | 3.900.253.596 | 0,000196 | 0,004892 |
| Quatro K | 25 | 3.904.533.816 | 0,000196 | 0,004897 |
| Quatro Q | 25 | 3.898.370.196 | 0,000196 | 0,004889 |
| Quatro J | 25 | 3.886.872.684 | 0,000195 | 0,004875 |
| Quatro 10 | 25 | 3.471.687.732 | 0,000174 | 0,004354 |
| Quatro 9 | 25 | 3.503.226.684 | 0,000176 | 0,004394 |
| Quatro 8 | 25 | 3.504.128.652 | 0,000176 | 0,004395 |
| Quatro 7 | 25 | 3.504.825.252 | 0,000176 | 0,004396 |
| Quatro 6 | 25 | 3.504.861.888 | 0,000176 | 0,004396 |
| Quatro 5 | 25 | 3.504.895.944 | 0,000176 | 0,004396 |
| Quatro 4 | 25 | 3.504.032.676 | 0,000176 | 0,004395 |
| Quatro 3 | 25 | 3.503.177.148 | 0,000176 | 0,004394 |
| Quatro 2 | 25 | 3.502.301.496 | 0,000176 | 0,004393 |
| Casa cheia | 9 | 229.475.482.596 | 0,011512 | 0,103610 |
| Descarga | 6 | 219.554.786.160 | 0,011015 | 0,066087 |
| Direto | 4 | 223.837.565.784 | 0,011229 | 0,044917 |
| Três de um tipo | 3 | 1.484.003.070.324 | 0,074449 | 0,223346 |
| Dois pares | 2 | 2.576.946.164.148 | 0,129279 | 0,258558 |
| Valetes ou melhor | 1 | 4.277.372.890.968 | 0,214585 | 0,214585 |
| Nada | 0 | 10.872.274.993.896 | 0,545435 | 0,000000 |
| Total | 19.933.230.517.200 | 1.000000 | 0,995439 |
A probabilidade de obter uma quadra qualquer é de 0,002363.
A próxima pergunta a ser respondida é: quantas quadras serão necessárias, em média, para obter todos os 13 tipos de cartas? Para responder a essa pergunta, criei minha Calculadora de Tentativas Esperadas . Para usá-la, insira o número de combinações de cada quadra nas primeiras 13 células. A calculadora informará que serão necessárias, em média, 41,532646 quadras para obter todos os 13 tipos de cartas.
Portanto, o número esperado de mãos jogadas para obter todas as 13 quadras é 41,341739/0,002363 = 17.580.
Um campo de grama pode alimentar exatamente:
Uma vaca e uma lhama durante 21 dias.
Uma lhama e uma ovelha durante 42 dias.
Uma ovelha e uma vaca durante 28 dias.
A vaca come tanta grama quanto a lhama e a ovelha juntas.
A grama cresce a uma taxa constante.
Quanto tempo levará para os três animais juntos devorarem completamente o campo de grama?
c = taxa de ingestão de grama pela vaca
l = taxa de lhama come grama
s = taxa de consumo de grama pelas ovelhas
g = taxa de crescimento da grama
Ao final de um período de tempo, a quantidade de grama consumida deve ser igual à quantidade inicial de grama mais a quantidade de grama que cresceu nesse período. Portanto...
(1) 21*(c+l) = 1 + 21g
(2) 42*(l+s) = 1+42g
(3) 28*(s+c) = 1+28g
Onde o número 1 representa um campo de grama.
Também nos é dado:
(4) c=s+l
Primeiro, substitua a equação (4) em (2):
(5) 42c = 1 + 42g
Expresse isso em termos de g:
(6) g = (42c-1)/42
Em seguida, substitua a equação (6) em (1)...
(7) 21(c+l) = 1 + 21*(42c-1)/42
Após um pouco de álgebra, chegamos a...
(8) l = 1/42.
Em seguida, substitua a equação (4) em (3)...
(9) 28*(2s + l) = 1+28g
Sabemos que l = 1/42, então...
28*(2s + 1/42) = 1+28g
56s + 28/42 = 1 + 28g
2352s + 28 = 42 + 1176g
(10) g = (2352s - 14)/1176
Em seguida, substitua as equações (8) e (10) em (2) ...
42*(1/42 + s) = 1 + 42*(2352s - 14)/1176
Após algumas operações algébricas simples, obtemos:
(11) s = 14/1176 = 1/84
Da equação (4)
(12) c = (1/84) + (1/42) = 3/84 = 1/28
Portanto, se a grama não crescesse, a vaca levaria 28 dias para comer o campo, a lhama 42 e a ovelha 84.
Em seguida, vamos resolver para g. Substitua (11) em (10):
g = [2352*(1/84)- 14]/1176
(13) g = 14/1176 = 1/84.
Por coincidência, essa é a mesma taxa em que a ovelha come a grama.
Seja t a resposta final. Sabemos que em t dias a quantidade de grama consumida deve ser igual à quantidade de grama no campo (1) mais a grama que cresceu nesse período. Então...
(13) t*(s+l+c) = 1 + tg
Resolvendo para t...
t*[(1/84) + (1/42) + (1/28)] = 1 + t/84
t = 1/[(1/84) + (1/42) + (1/28) - (1/84)]
(14) t = 84/5 = 16,8 dias = 16 dias, 19 horas e 12 minutos
Essa questão foi levantada e discutida no meu fórum no Wizard of Vegas.
Qual é a distância média entre dois pontos aleatórios em um quadrado unitário?
Para uma pergunta tão fácil de fazer, a solução é bastante complexa. Da forma como eu a resolvi, você precisará saber esta integral .
Aqui está a resposta e minha solução (PDF) .
Qual era o problema de matemática escrito no quadro-negro no filme Gênio Indomável ?
Na verdade, foi bem fácil, especialmente para um curso de matemática combinatória no MIT. Eis o enunciado do problema:
"Desenhe todas as árvores homeomorficamente irredutíveis de tamanho n=10."
Aqui está minha tentativa de explicar isso em inglês simples e direto.
Usando apenas linhas retas, desenhe todas as figuras onde a soma das interseções e dos becos sem saída seja igual a 10. Não pode haver nenhum laço fechado. Também não pode haver duas figuras equivalentes. Qualquer interseção deve ter pelo menos três caminhos partindo dela.
O que quero dizer com "equivalente", você pode perguntar? Significa que você pode mover as peças, deixando as interseções intactas, da maneira que quiser, e isso não criará nenhuma figura nova.
Aqui está um exemplo: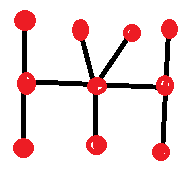
Vou dar uma dica. Ao contrário da resposta do filme, são dez. Will acertou apenas oito. Veja se você consegue igualar ou superar Will Hunting.
[spoiler]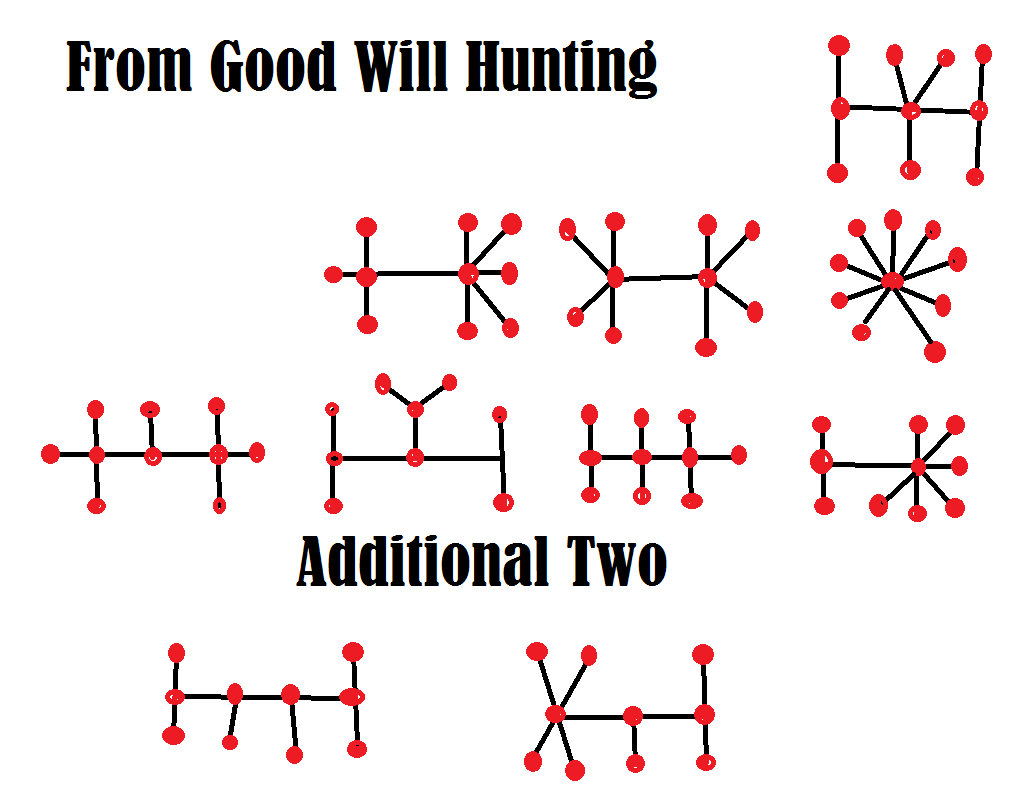
Apresento a minha lógica para chegar aos dez resultados no meu site MathProblems.info , problema 220.
[spoiler] Leitura complementar:- MATEMÁTICA EM GÊNIO INDOMÁVEL II: PROBLEMAS DA PERSPECTIVA DOS ALUNOS -- Artigo acadêmico sobre o problema.
- O PROBLEMA MATEMÁTICO DE "GÊNIO INDOMÁVEL" -- Discussão sobre o problema no meu fórum.
Considere um jogo com as seguintes regras:
- Um gerador de números aleatórios fornece números aleatórios entre 0 e 1, distribuídos uniformemente.
- Cada jogador recebe um número diferente. Cada jogador só pode ver o seu próprio número.
- O jogador 1 pode manter seu número inicial ou trocá-lo por um novo número aleatório.
- O jogador 2, sabendo da ação do jogador 1, tem a mesma opção de manter seu número original ou trocá-lo por um novo.
- O jogador com o número mais alto vence.
Tenho quatro perguntas sobre o jogo:
- Responda às seguintes perguntas sobre o jogo:
- Em que número o jogador 1 fica indiferente entre ficar parado e trocar de posição?
- Supondo que o jogador 1 troque de lado, em que número o jogador 2 ficará indiferente entre permanecer na mesma posição e trocar de lado?
- Supondo que o jogador 1 permaneça em pé, em que número o jogador 2 ficará indiferente entre permanecer em pé e trocar de posição?
- Considerando que ambos os jogadores adotem a estratégia ideal, qual é a probabilidade de o jogador 1 vencer?
A resposta e a solução podem ser encontradas na minha página de Problemas de Matemática , problema 225.
Estou participando de um bolão de mortes de 2018. Aqui estão as regras:
- Cada jogador deve enviar uma lista de dez celebridades vivas com menos de 100 anos de idade.
- Se alguma celebridade falecer, conforme evidenciado por uma menção da Associated Press, em 2018, então qualquer pessoa que tenha o nome da celebridade em sua lista receberá 100-x pontos, onde x é a idade da celebridade no momento da morte.
- O jogador com mais pontos em 01/01/2019 vence.
Levando em conta as médias, qual é a estratégia ideal para este jogo?
Como ex-atuário, você perguntou à pessoa certa. Espero que a Sociedade de Atuários não considere minha resposta um abuso da profissão. Dito isso, para responder à sua pergunta, consultei uma Tabela de Mortalidade Periódica de 2014 do meu antigo local de trabalho, o Gabinete do Atuário-Chefe da Administração da Previdência Social.
Uma tábua de mortalidade periódica mostra, entre outras coisas, a probabilidade de morte para uma pessoa de qualquer idade e sexo em 2014. Usando essa informação, criei a seguinte tabela, que mostra tanto a probabilidade de morte quanto a expectativa de vida para todas as idades de 0 a 100 anos e ambos os sexos.
Tabela de Mortalidade do Período de 2014
| Idade | Probabilidade de Morte — Masculino | Probabilidade de Morte — Feminina | Esperado Pontos — Masculino | Esperado Pontos — Feminino |
|---|---|---|---|---|
| 0 | 0,006320 | 0,005310 | 0,632000 | 0,531000 |
| 1 | 0,000403 | 0,000352 | 0,039852 | 0,034835 |
| 2 | 0,000282 | 0,000221 | 0,027626 | 0,021683 |
| 3 | 0,000211 | 0,000161 | 0,020514 | 0,015612 |
| 4 | 0,000181 | 0,000131 | 0,017405 | 0,012556 |
| 5 | 0,000161 | 0,000111 | 0,015313 | 0,010515 |
| 6 | 0,000141 | 0,000111 | 0,013260 | 0,010405 |
| 7 | 0,000131 | 0,000101 | 0,012184 | 0,009360 |
| 8 | 0,000121 | 0,000091 | 0,011127 | 0,008334 |
| 9 | 0,000091 | 0,000081 | 0,008256 | 0,007328 |
| 10 | 0,000101 | 0,000091 | 0,009073 | 0,008154 |
| 11 | 0,000101 | 0,000081 | 0,008973 | 0,007168 |
| 12 | 0,000131 | 0,000101 | 0,011535 | 0,008861 |
| 13 | 0,000202 | 0,000131 | 0,017547 | 0,011389 |
| 14 | 0,000303 | 0,000151 | 0,026023 | 0,012992 |
| 15 | 0,000404 | 0,000191 | 0,034304 | 0,016267 |
| 16 | 0,000505 | 0,000232 | 0,042393 | 0,019464 |
| 17 | 0,000616 | 0,000272 | 0,051129 | 0,022582 |
| 18 | 0,000748 | 0,000302 | 0,061316 | 0,024796 |
| 19 | 0,000880 | 0,000343 | 0,071262 | 0,027768 |
| 20 | 0,001022 | 0,000373 | 0,081780 | 0,029855 |
| 21 | 0,001145 | 0,000404 | 0,090445 | 0,031884 |
| 22 | 0,001258 | 0,000444 | 0,098105 | 0,034643 |
| 23 | 0,001310 | 0,000475 | 0,100880 | 0,036546 |
| 24 | 0,001332 | 0,000495 | 0,101246 | 0,037625 |
| 25 | 0,001344 | 0,000526 | 0,100811 | 0,039422 |
| 26 | 0,001377 | 0,000556 | 0,101864 | 0,041162 |
| 27 | 0,001389 | 0,000577 | 0,101371 | 0,042106 |
| 28 | 0,001421 | 0,000608 | 0,102330 | 0,043740 |
| 29 | 0,001454 | 0,000648 | 0,103234 | 0,046036 |
| 30 | 0,001507 | 0,000669 | 0,105517 | 0,046837 |
| 31 | 0,001530 | 0,000710 | 0,105584 | 0,048998 |
| 32 | 0,001574 | 0,000751 | 0,107011 | 0,051084 |
| 33 | 0,001617 | 0,000813 | 0,108364 | 0,054454 |
| 34 | 0,001661 | 0,000864 | 0,109644 | 0,057041 |
| 35 | 0,001716 | 0,000926 | 0,111521 | 0,060194 |
| 36 | 0,001781 | 0.001008 | 0,113970 | 0,064538 |
| 37 | 0,001857 | 0,001081 | 0,116963 | 0,068090 |
| 38 | 0,001933 | 0,001164 | 0,119830 | 0,072145 |
| 39 | 0,002020 | 0,001237 | 0,123207 | 0,075427 |
| 40 | 0,002118 | 0,001340 | 0,127066 | 0,080422 |
| 41 | 0,002258 | 0,001445 | 0,133232 | 0,085232 |
| 42 | 0,002410 | 0,001560 | 0,139778 | 0,090455 |
| 43 | 0,002615 | 0,001696 | 0,149075 | 0,096649 |
| 44 | 0,002843 | 0,001853 | 0,159228 | 0,103761 |
| 45 | 0,003105 | 0,002011 | 0,170771 | 0,110606 |
| 46 | 0,003401 | 0,002191 | 0,183635 | 0,118300 |
| 47 | 0,003742 | 0,002403 | 0,198314 | 0,127342 |
| 48 | 0,004108 | 0,002647 | 0,213613 | 0,137656 |
| 49 | 0,004532 | 0,002894 | 0,231133 | 0,147577 |
| 50 | 0,004994 | 0,003194 | 0,249696 | 0,159718 |
| 51 | 0,005473 | 0,003487 | 0,268191 | 0,170880 |
| 52 | 0,005993 | 0,003794 | 0,287656 | 0,182103 |
| 53 | 0,006565 | 0,004104 | 0,308561 | 0,192871 |
| 54 | 0,007159 | 0,004428 | 0,329324 | 0,203676 |
| 55 | 0,007799 | 0,004767 | 0,350946 | 0,214498 |
| 56 | 0,008475 | 0,005153 | 0,372902 | 0,226729 |
| 57 | 0,009179 | 0,005534 | 0,394696 | 0,237972 |
| 58 | 0,009856 | 0,005889 | 0,413944 | 0,247347 |
| 59 | 0,010575 | 0,006272 | 0,433558 | 0,257150 |
| 60 | 0,011350 | 0,006683 | 0,453991 | 0,267338 |
| 61 | 0,012209 | 0,007180 | 0,476135 | 0,280016 |
| 62 | 0,013061 | 0,007720 | 0,496330 | 0,293355 |
| 63 | 0,013921 | 0,008339 | 0,515084 | 0,308537 |
| 64 | 0,014814 | 0,009029 | 0,533320 | 0,325041 |
| 65 | 0,015831 | 0,009839 | 0,554094 | 0,344371 |
| 66 | 0,016981 | 0,010741 | 0,577354 | 0,365197 |
| 67 | 0,018300 | 0,011752 | 0,603909 | 0,387812 |
| 68 | 0,019778 | 0,012879 | 0,632894 | 0,412117 |
| 69 | 0,021443 | 0,014142 | 0,664734 | 0,438397 |
| 70 | 0,023384 | 0,015613 | 0,701513 | 0,468376 |
| 71 | 0,025547 | 0,017271 | 0,740873 | 0,500852 |
| 72 | 0,027877 | 0,019047 | 0,780560 | 0,533320 |
| 73 | 0,030384 | 0,020918 | 0,820374 | 0,564797 |
| 74 | 0,033098 | 0,022938 | 0,860535 | 0,596385 |
| 75 | 0,036256 | 0,025299 | 0,906400 | 0,632465 |
| 76 | 0,039868 | 0,028043 | 0,956841 | 0,673035 |
| 77 | 0,043883 | 0,031127 | 1,009299 | 0,715914 |
| 78 | 0,048257 | 0,034590 | 1,061657 | 0,760984 |
| 79 | 0,053128 | 0,038456 | 1,115692 | 0,807583 |
| 80 | 0,058709 | 0,043007 | 1,174177 | 0,860145 |
| 81 | 0,065070 | 0,048186 | 1,236322 | 0,915536 |
| 82 | 0,072149 | 0,053762 | 1,298691 | 0,967712 |
| 83 | 0,079906 | 0,059769 | 1,358409 | 1,016065 |
| 84 | 0,088524 | 0,066380 | 1,416378 | 1,062085 |
| 85 | 0,098157 | 0.073823 | 1,472348 | 1,107351 |
| 86 | 0,108904 | 0,082381 | 1,524651 | 1,153334 |
| 87 | 0,120889 | 0,092180 | 1,571556 | 1,198344 |
| 88 | 0,134134 | 0,103305 | 1,609607 | 1,239664 |
| 89 | 0,148707 | 0,115744 | 1,635778 | 1,273180 |
| 90 | 0,164522 | 0,129477 | 1,645220 | 1,294772 |
| 91 | 0,181584 | 0,144435 | 1,634254 | 1,299911 |
| 92 | 0,199903 | 0,160621 | 1,599225 | 1,284970 |
| 93 | 0,219362 | 0,177816 | 1,535534 | 1,244713 |
| 94 | 0,239881 | 0,196194 | 1,439286 | 1,177165 |
| 95 | 0,260293 | 0,214694 | 1,301463 | 1,073469 |
| 96 | 0,280129 | 0,233056 | 1.120515 | 0,932225 |
| 97 | 0,299042 | 0,251152 | 0,897125 | 0,753456 |
| 98 | 0,316317 | 0,268235 | 0,632634 | 0,536471 |
| 99 | 0,332667 | 0,284442 | 0,332667 | 0,284442 |
| 100 | 0,348651 | 0,301417 | 0,000000 | 0,000000 |
A tabela mostra que a pontuação máxima esperada é de 1,645220 para um homem de 90 anos.
Essa questão é levantada e discutida no meu fórum não relacionado a jogos de azar, Diversity Tomorrow .
Se você quiser colocar 355 mililitros em uma lata, quais devem ser as dimensões para minimizar a área da superfície?
Boa pergunta! Eu estava pensando exatamente isso quando vi umas latas de refrigerante fininhas numa feira de jogos, que tinham os mesmos 355 mililitros das latas de tamanho padrão. Com certeza as duas coisas não podem estar certas (e não me chame de Shirley).
r = raio da lata
h = altura da lata
v = volume da lata
s = área da superfície da lata
Sabemos por princípios básicos da geometria que a área da superfície é igual a 2πr² + 2πrh.
Da mesma forma, também sabemos que o volume é pi*r^2*h, que nos foi dado como sendo igual a 355.
Portanto, 355 = pi * r^2 * h.
Vamos reorganizar isso para:
(1) h = 355/(pi*r^2)
Nós sabemos:
(2) s = 2*pi*r^2 + 2*pi*r*h.
Vamos transformar isso em uma função de apenas uma variável, substituindo nossa expressão para h na equação (1) em (2):
s = 2*pi*r^2 + + 2*pi*r*(355/(pi*r^2))) = 2*pi*r^2 + 710/r.
Vamos calcular a derivada de s e igualá-la a zero para encontrar o valor ótimo de r.
ds/dr = 4*pi*r - 710/(r^2) = 0
4*pi*r = 710/(r^2)
Multiplicando ambos os lados por r^2:
4*pi*r^3 = 710
r^3 = 177,5/pi.
r = (177,5/pi)^(1/3) = 3,837215248.
Insira esse valor na equação (1) para obter h = 7,674430496.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
Pelo que percebo, a maioria dos profissionais de jogos de azar que conheço prefere saber a volatilidade de um jogo expressa em variância, em vez de desvio padrão. Claro, a primeira é apenas o quadrado do segundo. No entanto, eu prefiro o desvio padrão, já que está nas mesmas unidades da aposta e do ganho/perda. Talvez eles gostem de um número maior para destacar uma volatilidade maior? Qual a sua opinião? Existe alguma preferência entre os jogadores pelo uso da "variância" e, se sim, por quê?
Concordo que se ouve falar mais da variância de um jogo do que do seu desvio padrão, o que sempre me incomodou um pouco. Acredito que os jogadores deveriam se preocupar com a volatilidade de um jogo para associar uma vitória ou derrota a uma probabilidade em uma sessão de jogo. Por exemplo, o que seria uma perda de 1% após 200 mãos de blackjack? Para responder a essa pergunta, usaríamos o desvio padrão do blackjack, que é de cerca de 1,15, dependendo das regras.
A resposta específica para essa pergunta é 1,15 × 200^0,5 × -2,32635 (que é o ponto de 1% na curva gaussiana) = -37,83 unidades abaixo do esperado. Não se esqueça de que, devido à vantagem da casa, você pode esperar perder alguma coisa. Se assumirmos uma vantagem da casa de 0,3%, então, após 200 mãos, você poderia esperar perder 0,003 * 200 = 0,6 mãos. Portanto, uma perda ruim de 1% seria 0,6 + 37,83 = 38,43 mãos.
Ouvi dizer que a probabilidade de um casamento terminar em divórcio, geralmente citada como 50% nos Estados Unidos, é calculada dividindo-se o número de divórcios pelo número de casamentos no mesmo período. Isso é verdade? Você acha que essa é uma maneira justa de calcular a estatística? Questiono isso porque se trata de comparar divórcios em um curto período com casamentos realizados ao longo de um longo período.
Se a população e a distribuição etária fossem estáveis, e se a probabilidade de divórcio fosse realmente de 50%, esperaríamos observar uma proporção de um divórcio para cada dois casamentos em qualquer período de tempo, considerando uma amostra de grande porte.
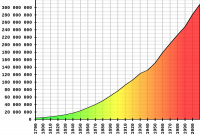
No entanto, a população não é estável. De acordo com este gráfico, parece que a população dos EUA está crescendo 10,71% por década. Isso equivale a 1,02% ao ano. Vamos arredondar para 1% para simplificar.
Fonte do mapa: Censo dos EUA
Segundo o site fatherly.com , a duração média de um casamento fracassado é de 8 anos.
Se você observasse uma proporção de 1 para 2 entre divórcios e casamentos atualmente, qual seria a probabilidade média de um casamento terminar em divórcio?
Os divórcios que vemos hoje são de casamentos ocorridos há 8 anos, quando a população era 92,35% da atual. Um cálculo simples sugere que a probabilidade real de divórcio é de 54,14%.
Vamos verificar isso.
Primeiro, de acordo com o CDC, há 6,9 casamentos para cada 1000 habitantes por ano. Esse dado não é relevante para a questão em pauta, mas acho que ajuda a visualizar os números envolvidos.
Suponha que a população há 8 anos era de 300.000.000. Isso representaria 0,69% * 300 milhões = 2.070.000 casamentos naquele ano.
Se 54,14% deles terminam em divórcio oito anos depois, então estaríamos vendo 2.070.000 * 54,14% = 1.120.698 divórcios atualmente.
1.120.698 / 2.070.000 = 50% da proporção observada de divórcios para casamentos na atualidade.
Para que ninguém diga nada, sim, eu sei que nem todos os divórcios terminam exatamente em oito anos. No entanto, considerando tudo, eu diria que o resultado final não ficará muito longe da minha taxa real de divórcio de 54,14%.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
Seu escritório com 100 funcionários realiza uma troca de presentes de Amigo Secreto. A ideia é escrever o nome de cada pessoa em pedaços de papel individuais, colocá-los em um chapéu e todos sorteiam um nome aleatoriamente para dar um presente.
A questão é: quantos ciclos fechados haverá, em média? Por exemplo, em um ciclo fechado, Gordon doa para Don, que doa para Jon, que doa para Nathan, que doa para Gordon. Ou sorteando seu próprio nome.
Considere que cada pessoa está escolhendo uma opção por vez. À medida que cada pessoa escolhe, haverá dois tipos de situações:
- O nome de quem escolher já foi escolhido.
- O nome de quem escolheu ainda está na caixa de nomes.
Para qualquer pessoa que esteja selecionando, digamos que restem n pessoas para selecionar.
Se o nome de quem está escolhendo já tiver sido escolhido, há uma chance de 1/n de que a pessoa que está escolhendo feche um ciclo envolvendo seu nome. Por exemplo, digamos que Amy esteja escolhendo. O nome de Amy já pertence a Bob, o nome de Bob já pertence a Charlie e o nome de Charlie ainda está no recipiente. Com n nomes ainda no recipiente, há uma chance de 1/n de que Amy escolha o nome de Charlie, fechando um ciclo.
Se o nome de quem está escolhendo ainda não tiver sido escolhido, há uma chance de 1/n de Amy escolher o próprio nome, fechando o ciclo.
De qualquer forma, se a pessoa que recolhe os itens não fechar um ciclo, ela estará entrando em outra cadeia, que eventualmente será fechada por outra pessoa. Cada cadeia deve ser contada apenas uma vez, quando for fechada.
Assim, a resposta é 1/100 + 1/99 + 1/98 + ... + 1/1 = ~ 5,187377518.
Uma estimativa para qualquer número suficientemente grande de jogadores, n, é ln(n).
A questão é levantada e discutida no meu fórum, Wizard of Vegas .
Em homenagem à coluna Pergunte ao Mago nº 314, quais são suas séries infinitas favoritas cuja soma resulta em alguma função de pi?
É fácil escolher estes dois, provavelmente os dois mais famosos:
- 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... = π/4
- 1/1 ^ 2 + 1/2 ^ 2 + 1/3 ^ 2 + 1/4 ^ 2 + ... = π ^ 2/6
Ouvi dizer que, em um grupo de 23 pessoas aleatórias, a probabilidade de pelo menos duas ou mais pessoas terem o mesmo aniversário é superior a 50%. Isso é verdade? Qual a probabilidade de haver um aniversário em comum para outros tamanhos de grupo? A mesma pergunta se aplica a grupos de 3, 4 e 5 pessoas que fazem aniversário.
É verdade, com 23 pessoas escolhidas aleatoriamente, a probabilidade de pelo menos um par de pessoas ter aniversário no mesmo dia é de 50,73%. Isso ignora o dia bissexto e assume que todos têm a mesma chance de nascer em cada um dos outros 365 dias (o que não é o caso na realidade, já que aniversários na primavera e no outono são ligeiramente mais comuns).
As tabelas em resposta à sua pergunta são bastante extensas, então vou colocá-las em spoilers. Clique nos botões para ver as respostas.
Aniversário em comum para 2 ou mais pessoas
| Tamanho do grupo | Probabilidade |
|---|---|
| 2 | 0,002740 |
| 3 | 0,008204 |
| 4 | 0,016356 |
| 5 | 0,027136 |
| 6 | 0,040462 |
| 7 | 0,056236 |
| 8 | 0,074335 |
| 9 | 0,094624 |
| 10 | 0,116948 |
| 11 | 0,141141 |
| 12 | 0,167025 |
| 13 | 0,194410 |
| 14 | 0,223103 |
| 15 | 0,252901 |
| 16 | 0,283604 |
| 17 | 0,315008 |
| 18 | 0,346911 |
| 19 | 0,379119 |
| 20 | 0,411438 |
| 21 | 0,443688 |
| 22 | 0,475695 |
| 23 | 0,507297 |
| 24 | 0,538344 |
| 25 | 0,568700 |
| 26 | 0,598241 |
| 27 | 0,626859 |
| 28 | 0,654461 |
| 29 | 0,680969 |
| 30 | 0,706316 |
| 31 | 0,730455 |
| 32 | 0,753348 |
| 33 | 0,774972 |
| 34 | 0,795317 |
| 35 | 0,814383 |
| 36 | 0,832182 |
| 37 | 0,848734 |
| 38 | 0,864068 |
| 39 | 0,878220 |
| 40 | 0,891232 |
| 41 | 0,903152 |
| 42 | 0,914030 |
| 43 | 0,923923 |
| 44 | 0,932885 |
| 45 | 0,940976 |
| 46 | 0,948253 |
| 47 | 0,954774 |
| 48 | 0,960598 |
| 49 | 0,965780 |
| 50 | 0,970374 |
| 51 | 0,974432 |
| 52 | 0,978005 |
| 53 | 0,981138 |
| 54 | 0,983877 |
| 55 | 0,986262 |
| 56 | 0,988332 |
| 57 | 0,990122 |
| 58 | 0,991665 |
| 59 | 0,992989 |
| 60 | 0,994123 |
| 61 | 0,995089 |
| 62 | 0,995910 |
| 63 | 0,996604 |
| 64 | 0,997190 |
| 65 | 0,997683 |
| 66 | 0,998096 |
| 67 | 0,998440 |
| 68 | 0,998726 |
| 69 | 0,998964 |
| 70 | 0,999160 |
| 71 | 0,999321 |
| 72 | 0,999453 |
| 73 | 0,999561 |
| 74 | 0,999649 |
| 75 | 0,999720 |
| 76 | 0,999777 |
| 77 | 0,999824 |
| 78 | 0,999861 |
| 79 | 0,999891 |
| 80 | 0,999914 |
| 81 | 0,999933 |
| 82 | 0,999948 |
| 83 | 0,999960 |
| 84 | 0,999969 |
Aniversário em comum de 3 ou mais pessoas
| Tamanho do grupo | Probabilidade |
|---|---|
| 3 | 0,000008 |
| 4 | 0,000030 |
| 5 | 0,000075 |
| 6 | 0,000149 |
| 7 | 0,000261 |
| 8 | 0,000416 |
| 9 | 0,000623 |
| 10 | 0,000888 |
| 11 | 0,001218 |
| 12 | 0,001621 |
| 13 | 0,002102 |
| 14 | 0,002670 |
| 15 | 0,003329 |
| 16 | 0,004088 |
| 17 | 0,004953 |
| 18 | 0,005929 |
| 19 | 0,007024 |
| 20 | 0,008243 |
| 21 | 0,009592 |
| 22 | 0,011078 |
| 23 | 0,012705 |
| 24 | 0,014481 |
| 25 | 0,016409 |
| 26 | 0,018497 |
| 27 | 0,020747 |
| 28 | 0,023167 |
| 29 | 0,025760 |
| 30 | 0,028531 |
| 31 | 0,031484 |
| 32 | 0,034624 |
| 33 | 0,037954 |
| 34 | 0,041479 |
| 35 | 0,045202 |
| 36 | 0,049126 |
| 37 | 0,053254 |
| 38 | 0,057589 |
| 39 | 0,062133 |
| 40 | 0,066889 |
| 41 | 0,071859 |
| 42 | 0,077044 |
| 43 | 0,082446 |
| 44 | 0,088065 |
| 45 | 0,093903 |
| 46 | 0,099960 |
| 47 | 0,106236 |
| 48 | 0,112731 |
| 49 | 0,119444 |
| 50 | 0,126375 |
| 51 | 0,133522 |
| 52 | 0,140885 |
| 53 | 0,148460 |
| 54 | 0,156246 |
| 55 | 0,164241 |
| 56 | 0,172441 |
| 57 | 0,180844 |
| 58 | 0,189445 |
| 59 | 0,198242 |
| 60 | 0,207230 |
| 61 | 0,216405 |
| 62 | 0,225761 |
| 63 | 0,235294 |
| 64 | 0,244999 |
| 65 | 0,254869 |
| 66 | 0,264899 |
| 67 | 0,275082 |
| 68 | 0,285413 |
| 69 | 0,295883 |
| 70 | 0,306487 |
| 71 | 0,317217 |
| 72 | 0,328066 |
| 73 | 0,339026 |
| 74 | 0,350088 |
| 75 | 0,361246 |
| 76 | 0,372491 |
| 77 | 0,383814 |
| 78 | 0,395207 |
| 79 | 0,406662 |
| 80 | 0,418169 |
| 81 | 0,429720 |
| 82 | 0,441307 |
| 83 | 0,452920 |
| 84 | 0,464550 |
| 85 | 0,476188 |
| 86 | 0,487826 |
| 87 | 0,499455 |
| 88 | 0,511065 |
| 89 | 0,522648 |
| 90 | 0,534196 |
| 91 | 0,545698 |
| 92 | 0,557148 |
| 93 | 0,568537 |
| 94 | 0,579855 |
| 95 | 0,591096 |
| 96 | 0,602252 |
| 97 | 0,613314 |
| 98 | 0,624275 |
| 99 | 0,635127 |
| 100 | 0,645865 |
| 101 | 0,656480 |
| 102 | 0,666967 |
| 103 | 0,677318 |
| 104 | 0.687529 |
| 105 | 0,697593 |
| 106 | 0,707505 |
| 107 | 0,717260 |
| 108 | 0,726853 |
| 109 | 0,736279 |
| 110 | 0,745536 |
| 111 | 0,754619 |
| 112 | 0,763525 |
| 113 | 0,772251 |
| 114 | 0,780795 |
| 115 | 0,789155 |
| 116 | 0,797330 |
| 117 | 0,805319 |
| 118 | 0,813121 |
| 119 | 0,820580 |
| 120 | 0,827964 |
| 121 | 0,835152 |
| 122 | 0,842144 |
| 123 | 0,848940 |
| 124 | 0,855540 |
| 125 | 0,861945 |
| 126 | 0,868155 |
| 127 | 0,874172 |
| 128 | 0,879996 |
| 129 | 0,885631 |
| 130 | 0,891076 |
| 131 | 0,896335 |
| 132 | 0,901409 |
| 133 | 0,906302 |
| 134 | 0,911015 |
| 135 | 0,915552 |
| 136 | 0,919915 |
| 137 | 0,924108 |
| 138 | 0,928135 |
| 139 | 0,931997 |
| 140 | 0,935700 |
| 141 | 0,939246 |
| 142 | 0,942640 |
| 143 | 0,945885 |
| 144 | 0,948985 |
| 145 | 0,951944 |
| 146 | 0,954766 |
| 147 | 0,957456 |
| 148 | 0,960016 |
| 149 | 0,962452 |
| 150 | 0,964767 |
| 151 | 0,966965 |
| 152 | 0,969050 |
| 153 | 0,971028 |
| 154 | 0,972900 |
| 155 | 0,974672 |
| 156 | 0,976347 |
| 157 | 0,977930 |
| 158 | 0,979423 |
| 159 | 0,980831 |
| 160 | 0,982158 |
| 161 | 0,983407 |
| 162 | 0,984581 |
| 163 | 0,985684 |
| 164 | 0,986719 |
| 165 | 0,987690 |
| 166 | 0,988600 |
| 167 | 0,989452 |
| 168 | 0,990248 |
| 169 | 0,990992 |
| 170 | 0,991687 |
| 171 | 0,992335 |
| 172 | 0,992938 |
| 173 | 0,993500 |
| 174 | 0,994022 |
| 175 | 0,994508 |
| 176 | 0,994958 |
| 177 | 0,995376 |
| 178 | 0,995763 |
| 179 | 0,996121 |
| 180 | 0,996452 |
| 181 | 0,996758 |
| 182 | 0,997040 |
| 183 | 0,997300 |
| 184 | 0,997540 |
| 185 | 0,997760 |
| 186 | 0,997963 |
| 187 | 0,998149 |
| 188 | 0,998319 |
| 189 | 0,998476 |
| 190 | 0,998619 |
| 191 | 0,998750 |
| 192 | 0,998869 |
| 193 | 0,998979 |
| 194 | 0,999078 |
| 195 | 0,999169 |
| 196 | 0,999251 |
| 197 | 0,999326 |
| 198 | 0,999394 |
| 199 | 0,999456 |
| 200 | 0,999512 |
| 201 | 0,999562 |
| 202 | 0,999608 |
| 203 | 0,999650 |
| 204 | 0,999687 |
| 205 | 0,999720 |
| 206 | 0,999751 |
| 207 | 0,999778 |
| 208 | 0,999802 |
| 209 | 0,999824 |
| 210 | 0,999844 |
| 211 | 0,999862 |
| 212 | 0,999877 |
| 213 | 0,999891 |
| 214 | 0,999904 |
| 215 | 0.999915 |
| 216 | 0,999925 |
| 217 | 0,999934 |
| 218 | 0,999942 |
| 219 | 0,999949 |
| 220 | 0,999955 |
| 221 | 0,999961 |
| 222 | 0,999966 |
| 223 | 0,999970 |
| 224 | 0,999974 |
| 225 | 0,999977 |
| 226 | 0,999980 |
| 227 | 0,999982 |
| 228 | 0,999985 |
| 229 | 0,999987 |
| 230 | 0,999988 |
| 231 | 0,999990 |
| 232 | 0,999991 |
| 233 | 0,999992 |
| 234 | 0,999994 |
| 235 | 0,999994 |
| 236 | 0,999995 |
| 237 | 0,999996 |
| 238 | 0,999996 |
| 239 | 0,999997 |
| 240 | 0,999997 |
| 241 | 0,999998 |
| 242 | 0,999998 |
| 243 | 0,999998 |
| 244 | 0,999999 |
Aniversário em comum para 4 ou mais pessoas
| Tamanho do grupo | Probabilidade |
|---|---|
| 4 | 0,000000 |
| 5 | 0,000000 |
| 6 | 0,000000 |
| 7 | 0,000001 |
| 8 | 0,000001 |
| 9 | 0,000003 |
| 10 | 0,000004 |
| 11 | 0,000007 |
| 12 | 0,000010 |
| 13 | 0,000014 |
| 14 | 0,000020 |
| 15 | 0,000027 |
| 16 | 0,000036 |
| 17 | 0,000048 |
| 18 | 0,000061 |
| 19 | 0,000077 |
| 20 | 0,000096 |
| 21 | 0,000119 |
| 22 | 0,000145 |
| 23 | 0,000175 |
| 24 | 0,000209 |
| 25 | 0,000248 |
| 26 | 0,000293 |
| 27 | 0,000343 |
| 28 | 0,000399 |
| 29 | 0,000462 |
| 30 | 0,000532 |
| 31 | 0,000610 |
| 32 | 0,000695 |
| 33 | 0,000790 |
| 34 | 0,000893 |
| 35 | 0,001006 |
| 36 | 0,001129 |
| 37 | 0,001263 |
| 38 | 0,001408 |
| 39 | 0,001566 |
| 40 | 0,001736 |
| 41 | 0,001919 |
| 42 | 0,002116 |
| 43 | 0,002328 |
| 44 | 0,002555 |
| 45 | 0,002798 |
| 46 | 0,003058 |
| 47 | 0,003334 |
| 48 | 0,003629 |
| 49 | 0,003943 |
| 50 | 0,004276 |
| 51 | 0,004629 |
| 52 | 0,005003 |
| 53 | 0,005399 |
| 54 | 0,005817 |
| 55 | 0,006258 |
| 56 | 0,006724 |
| 57 | 0,007214 |
| 58 | 0,007730 |
| 59 | 0,008272 |
| 60 | 0,008841 |
| 61 | 0,009439 |
| 62 | 0,010065 |
| 63 | 0,010721 |
| 64 | 0,011408 |
| 65 | 0,012126 |
| 66 | 0,012876 |
| 67 | 0,013659 |
| 68 | 0,014476 |
| 69 | 0,015327 |
| 70 | 0,016215 |
| 71 | 0,017139 |
| 72 | 0,018100 |
| 73 | 0,019099 |
| 74 | 0,020137 |
| 75 | 0,021215 |
| 76 | 0,022334 |
| 77 | 0,023495 |
| 78 | 0,024698 |
| 79 | 0,025944 |
| 80 | 0,027235 |
| 81 | 0,028570 |
| 82 | 0,029951 |
| 83 | 0,031379 |
| 84 | 0,032855 |
| 85 | 0,034379 |
| 86 | 0,035952 |
| 87 | 0,037575 |
| 88 | 0,039249 |
| 89 | 0,040974 |
| 90 | 0,042752 |
| 91 | 0,044583 |
| 92 | 0,046467 |
| 93 | 0,048407 |
| 94 | 0,050402 |
| 95 | 0,052453 |
| 96 | 0,054561 |
| 97 | 0,056726 |
| 98 | 0,058950 |
| 99 | 0,061233 |
| 100 | 0,063576 |
| 101 | 0,065978 |
| 102 | 0,068442 |
| 103 | 0,070967 |
| 104 | 0,073554 |
| 105 | 0.076204 |
| 106 | 0,078917 |
| 107 | 0,081694 |
| 108 | 0,084535 |
| 109 | 0,087441 |
| 110 | 0,090412 |
| 111 | 0,093449 |
| 112 | 0,096552 |
| 113 | 0,099722 |
| 114 | 0,102958 |
| 115 | 0,106262 |
| 116 | 0,109633 |
| 117 | 0,113072 |
| 118 | 0,116579 |
| 119 | 0,120154 |
| 120 | 0,123798 |
| 121 | 0,127510 |
| 122 | 0,131292 |
| 123 | 0,135142 |
| 124 | 0,139061 |
| 125 | 0,143050 |
| 126 | 0,147107 |
| 127 | 0,151234 |
| 128 | 0,155429 |
| 129 | 0,159694 |
| 130 | 0,164027 |
| 131 | 0,168429 |
| 132 | 0,172899 |
| 133 | 0,177438 |
| 134 | 0,182044 |
| 135 | 0,186719 |
| 136 | 0,191460 |
| 137 | 0,196269 |
| 138 | 0,201144 |
| 139 | 0,206085 |
| 140 | 0,211091 |
| 141 | 0,216163 |
| 142 | 0,221299 |
| 143 | 0,226499 |
| 144 | 0,231763 |
| 145 | 0,237089 |
| 146 | 0,242476 |
| 147 | 0,247925 |
| 148 | 0,253434 |
| 149 | 0,259002 |
| 150 | 0,264629 |
| 151 | 0,270314 |
| 152 | 0,276055 |
| 153 | 0,281852 |
| 154 | 0,287703 |
| 155 | 0,293608 |
| 156 | 0,299566 |
| 157 | 0,305575 |
| 158 | 0,311634 |
| 159 | 0,317741 |
| 160 | 0,323897 |
| 161 | 0,330099 |
| 162 | 0,336346 |
| 163 | 0,342637 |
| 164 | 0,348970 |
| 165 | 0,355343 |
| 166 | 0,361757 |
| 167 | 0,368208 |
| 168 | 0,374696 |
| 169 | 0,381218 |
| 170 | 0,387774 |
| 171 | 0,394362 |
| 172 | 0,400980 |
| 173 | 0,407626 |
| 174 | 0,414299 |
| 175 | 0,420997 |
| 176 | 0,427718 |
| 177 | 0,434462 |
| 178 | 0,441224 |
| 179 | 0,448005 |
| 180 | 0,454803 |
| 181 | 0,461615 |
| 182 | 0,468439 |
| 183 | 0,475274 |
| 184 | 0,482118 |
| 185 | 0,488969 |
| 186 | 0,495826 |
| 187 | 0,502685 |
| 188 | 0,509546 |
| 189 | 0,516407 |
| 190 | 0,523265 |
| 191 | 0,530119 |
| 192 | 0,536967 |
| 193 | 0,543807 |
| 194 | 0,550636 |
| 195 | 0,557454 |
| 196 | 0,564258 |
| 197 | 0,571046 |
| 198 | 0,577817 |
| 199 | 0,584568 |
| 200 | 0,591298 |
| 201 | 0,598005 |
| 202 | 0,604687 |
| 203 | 0,611342 |
| 204 | 0,617969 |
| 205 | 0,624565 |
| 206 | 0,631129 |
| 207 | 0,637659 |
| 208 | 0,644154 |
| 209 | 0,650611 |
| 210 | 0,657030 |
| 211 | 0,663407 |
| 212 | 0,669743 |
| 213 | 0,676035 |
| 214 | 0,682281 |
| 215 | 0,688481 |
| 216 | 0.694632 |
| 217 | 0,700734 |
| 218 | 0,706784 |
| 219 | 0,712782 |
| 220 | 0,718726 |
| 221 | 0,724614 |
| 222 | 0,730446 |
| 223 | 0,736220 |
| 224 | 0,741936 |
| 225 | 0,747591 |
| 226 | 0,753185 |
| 227 | 0,758717 |
| 228 | 0,764185 |
| 229 | 0,769590 |
| 230 | 0,774929 |
| 231 | 0,780202 |
| 232 | 0,785409 |
| 233 | 0,790547 |
| 234 | 0,795618 |
| 235 | 0,800619 |
| 236 | 0,805551 |
| 237 | 0,810412 |
| 238 | 0,815202 |
| 239 | 0,819921 |
| 240 | 0,824569 |
| 241 | 0,829144 |
| 242 | 0,833646 |
| 243 | 0,838076 |
| 244 | 0,842432 |
| 245 | 0,846716 |
| 246 | 0,850925 |
| 247 | 0,855061 |
| 248 | 0,859123 |
| 249 | 0,863112 |
| 250 | 0,867027 |
| 251 | 0,870868 |
| 252 | 0,874635 |
| 253 | 0,878329 |
| 254 | 0,881950 |
| 255 | 0,885498 |
| 256 | 0,888973 |
| 257 | 0,892375 |
| 258 | 0,895705 |
| 259 | 0,898964 |
| 260 | 0,902151 |
| 261 | 0,905268 |
| 262 | 0,908314 |
| 263 | 0,911290 |
| 264 | 0,914197 |
| 265 | 0,917036 |
| 266 | 0,919806 |
| 267 | 0,922509 |
| 268 | 0,925145 |
| 269 | 0,927715 |
| 270 | 0,930220 |
| 271 | 0,932661 |
| 272 | 0,935037 |
| 273 | 0,937351 |
| 274 | 0,939603 |
| 275 | 0,941793 |
| 276 | 0,943923 |
| 277 | 0,945993 |
| 278 | 0,948005 |
| 279 | 0,949960 |
| 280 | 0,951857 |
| 281 | 0,953699 |
| 282 | 0,955486 |
| 283 | 0,957218 |
| 284 | 0,958898 |
| 285 | 0,960527 |
| 286 | 0,962104 |
| 287 | 0,963631 |
| 288 | 0,965109 |
| 289 | 0,966540 |
| 290 | 0,967923 |
| 291 | 0,969260 |
| 292 | 0,970553 |
| 293 | 0,971802 |
| 294 | 0,973007 |
| 295 | 0,974171 |
| 296 | 0,975294 |
| 297 | 0,976377 |
| 298 | 0,977421 |
| 299 | 0,978427 |
| 300 | 0,979397 |
| 301 | 0,980330 |
| 302 | 0,981228 |
| 303 | 0,982092 |
| 304 | 0,982923 |
| 305 | 0,983722 |
| 306 | 0,984490 |
| 307 | 0,985227 |
| 308 | 0,985935 |
| 309 | 0,986614 |
| 310 | 0,987266 |
| 311 | 0,987890 |
| 312 | 0,988489 |
| 313 | 0,989063 |
| 314 | 0,989612 |
| 315 | 0,990138 |
| 316 | 0,990641 |
| 317 | 0,991122 |
| 318 | 0,991581 |
| 319 | 0,992021 |
| 320 | 0,992440 |
| 321 | 0,992841 |
| 322 | 0,993223 |
| 323 | 0,993587 |
| 324 | 0,993935 |
| 325 | 0,994266 |
| 326 | 0,994581 |
| 327 | 0.994882 |
| 328 | 0,995167 |
| 329 | 0,995439 |
| 330 | 0,995698 |
| 331 | 0,995943 |
| 332 | 0,996176 |
| 333 | 0,996398 |
| 334 | 0,996608 |
| 335 | 0,996807 |
| 336 | 0,996996 |
| 337 | 0,997175 |
| 338 | 0,997344 |
| 339 | 0,997505 |
| 340 | 0,997657 |
| 341 | 0,997801 |
| 342 | 0,997936 |
| 343 | 0,998065 |
| 344 | 0,998186 |
| 345 | 0,998300 |
| 346 | 0,998408 |
| 347 | 0,998510 |
| 348 | 0,998606 |
| 349 | 0,998696 |
| 350 | 0,998781 |
| 351 | 0,998861 |
| 352 | 0,998937 |
| 353 | 0,999008 |
| 354 | 0,999074 |
| 355 | 0,999137 |
| 356 | 0,999195 |
| 357 | 0,999250 |
| 358 | 0,999302 |
| 359 | 0,999350 |
| 360 | 0,999396 |
| 361 | 0,999438 |
| 362 | 0,999478 |
| 363 | 0,999515 |
| 364 | 0,999550 |
| 365 | 0,999582 |
| 366 | 0,999613 |
| 367 | 0,999641 |
| 368 | 0,999668 |
| 369 | 0,999692 |
| 370 | 0,999715 |
| 371 | 0,999736 |
| 372 | 0,999756 |
| 373 | 0,999775 |
| 374 | 0,999792 |
| 375 | 0,999808 |
| 376 | 0,999823 |
| 377 | 0,999837 |
| 378 | 0,999850 |
| 379 | 0,999861 |
| 380 | 0,999872 |
| 381 | 0,999883 |
| 382 | 0,999892 |
| 383 | 0,999901 |
| 384 | 0,999909 |
| 385 | 0,999916 |
| 386 | 0,999923 |
| 387 | 0,999930 |
| 388 | 0,999935 |
| 389 | 0,999941 |
| 390 | 0,999946 |
| 391 | 0,999950 |
| 392 | 0,999955 |
| 393 | 0,999959 |
| 394 | 0,999962 |
| 395 | 0,999965 |
| 396 | 0,999969 |
| 397 | 0,999971 |
| 398 | 0,999974 |
| 399 | 0,999976 |
| 400 | 0,999978 |
| 401 | 0,999980 |
| 402 | 0,999982 |
| 403 | 0,999984 |
| 404 | 0,999985 |
| 405 | 0,999987 |
| 406 | 0,999988 |
| 407 | 0,999989 |
| 408 | 0,999990 |
| 409 | 0,999991 |
| 410 | 0,999992 |
| 411 | 0,999993 |
| 412 | 0,999993 |
| 413 | 0,999994 |
| 414 | 0,999995 |
| 415 | 0,999995 |
| 416 | 0,999996 |
| 417 | 0,999996 |
| 418 | 0,999996 |
| 419 | 0,999997 |
| 420 | 0,999997 |
| 421 | 0,999997 |
| 422 | 0,999998 |
| 423 | 0,999998 |
| 424 | 0,999998 |
| 425 | 0,999998 |
| 426 | 0,999998 |
| 427 | 0,999999 |
| 428 | 0,999999 |
| 429 | 0,999999 |
Aniversário em comum de 5 ou mais pessoas
| Tamanho do grupo | Probabilidade |
|---|---|
| 5 | 0,000000 |
| 6 | 0,000000 |
| 7 | 0,000000 |
| 8 | 0,000000 |
| 9 | 0,000000 |
| 10 | 0,000000 |
| 11 | 0,000000 |
| 12 | 0,000000 |
| 13 | 0,000000 |
| 14 | 0,000000 |
| 15 | 0,000000 |
| 16 | 0,000000 |
| 17 | 0,000000 |
| 18 | 0,000001 |
| 19 | 0,000001 |
| 20 | 0,000001 |
| 21 | 0,000001 |
| 22 | 0,000002 |
| 23 | 0,000002 |
| 24 | 0,000003 |
| 25 | 0,000004 |
| 26 | 0,000004 |
| 27 | 0,000005 |
| 28 | 0,000006 |
| 29 | 0,000008 |
| 30 | 0,000009 |
| 31 | 0,000011 |
| 32 | 0,000013 |
| 33 | 0,000015 |
| 34 | 0,000017 |
| 35 | 0,000020 |
| 36 | 0,000023 |
| 37 | 0,000026 |
| 38 | 0,000030 |
| 39 | 0,000034 |
| 40 | 0,000039 |
| 41 | 0,000044 |
| 42 | 0,000050 |
| 43 | 0,000056 |
| 44 | 0,000063 |
| 45 | 0,000070 |
| 46 | 0,000079 |
| 47 | 0,000087 |
| 48 | 0,000097 |
| 49 | 0,000108 |
| 50 | 0,000119 |
| 51 | 0,000132 |
| 52 | 0,000145 |
| 53 | 0,000159 |
| 54 | 0,000175 |
| 55 | 0,000192 |
| 56 | 0,000209 |
| 57 | 0,000229 |
| 58 | 0,000249 |
| 59 | 0,000271 |
| 60 | 0,000295 |
| 61 | 0,000320 |
| 62 | 0,000347 |
| 63 | 0,000375 |
| 64 | 0,000406 |
| 65 | 0,000438 |
| 66 | 0,000472 |
| 67 | 0,000509 |
| 68 | 0,000547 |
| 69 | 0,000588 |
| 70 | 0,000631 |
| 71 | 0,000676 |
| 72 | 0,000725 |
| 73 | 0,000775 |
| 74 | 0,000829 |
| 75 | 0,000885 |
| 76 | 0,000944 |
| 77 | 0,001007 |
| 78 | 0,001072 |
| 79 | 0,001141 |
| 80 | 0,001213 |
| 81 | 0,001289 |
| 82 | 0,001369 |
| 83 | 0,001452 |
| 84 | 0,001539 |
| 85 | 0,001630 |
| 86 | 0,001726 |
| 87 | 0,001825 |
| 88 | 0,001930 |
| 89 | 0,002038 |
| 90 | 0,002152 |
| 91 | 0,002270 |
| 92 | 0,002394 |
| 93 | 0,002522 |
| 94 | 0,002656 |
| 95 | 0,002796 |
| 96 | 0,002941 |
| 97 | 0,003092 |
| 98 | 0,003249 |
| 99 | 0,003412 |
| 100 | 0,003581 |
| 101 | 0,003757 |
| 102 | 0,003939 |
| 103 | 0,004128 |
| 104 | 0,004325 |
| 105 | 0,004528 |
| 106 | 0.004739 |
| 107 | 0,004957 |
| 108 | 0,005183 |
| 109 | 0,005417 |
| 110 | 0,005659 |
| 111 | 0,005909 |
| 112 | 0,006168 |
| 113 | 0,006436 |
| 114 | 0,006712 |
| 115 | 0,006998 |
| 116 | 0,007293 |
| 117 | 0,007597 |
| 118 | 0,007912 |
| 119 | 0,008236 |
| 120 | 0,008570 |
| 121 | 0,008915 |
| 122 | 0,009270 |
| 123 | 0,009636 |
| 124 | 0,010013 |
| 125 | 0,010402 |
| 126 | 0,010801 |
| 127 | 0,011213 |
| 128 | 0,011637 |
| 129 | 0,012072 |
| 130 | 0,012521 |
| 131 | 0,012981 |
| 132 | 0,013455 |
| 133 | 0,013942 |
| 134 | 0,014442 |
| 135 | 0,014956 |
| 136 | 0,015484 |
| 137 | 0,016026 |
| 138 | 0,016582 |
| 139 | 0,017153 |
| 140 | 0,017739 |
| 141 | 0,018340 |
| 142 | 0,018956 |
| 143 | 0,019588 |
| 144 | 0,020235 |
| 145 | 0,020899 |
| 146 | 0,021580 |
| 147 | 0,022277 |
| 148 | 0,022991 |
| 149 | 0,023722 |
| 150 | 0,024470 |
| 151 | 0,025237 |
| 152 | 0,026021 |
| 153 | 0,026824 |
| 154 | 0,027645 |
| 155 | 0,028485 |
| 156 | 0,029344 |
| 157 | 0,030222 |
| 158 | 0,031120 |
| 159 | 0,032037 |
| 160 | 0,032975 |
| 161 | 0,033934 |
| 162 | 0,034913 |
| 163 | 0,035912 |
| 164 | 0,036934 |
| 165 | 0,037976 |
| 166 | 0,039040 |
| 167 | 0,040127 |
| 168 | 0,041235 |
| 169 | 0,042367 |
| 170 | 0,043521 |
| 171 | 0,044698 |
| 172 | 0,045898 |
| 173 | 0,047122 |
| 174 | 0,048370 |
| 175 | 0,049642 |
| 176 | 0,050939 |
| 177 | 0,052260 |
| 178 | 0,053606 |
| 179 | 0,054977 |
| 180 | 0,056374 |
| 181 | 0,057796 |
| 182 | 0,059245 |
| 183 | 0,060719 |
| 184 | 0,062220 |
| 185 | 0,063748 |
| 186 | 0,065302 |
| 187 | 0,066884 |
| 188 | 0,068493 |
| 189 | 0,070130 |
| 190 | 0,071795 |
| 191 | 0,073487 |
| 192 | 0,075209 |
| 193 | 0,076958 |
| 194 | 0,078737 |
| 195 | 0,080544 |
| 196 | 0,082381 |
| 197 | 0,084247 |
| 198 | 0,086143 |
| 199 | 0,088068 |
| 200 | 0,090024 |
| 201 | 0,092009 |
| 202 | 0,094026 |
| 203 | 0,096072 |
| 204 | 0,098150 |
| 205 | 0,100259 |
| 206 | 0,102398 |
| 207 | 0,104569 |
| 208 | 0,106772 |
| 209 | 0,109006 |
| 210 | 0,111272 |
| 211 | 0,113570 |
| 212 | 0,115899 |
| 213 | 0,118262 |
| 214 | 0,120656 |
| 215 | 0,123083 |
| 216 | 0,125542 |
| 217 | 0.128035 |
| 218 | 0,130559 |
| 219 | 0,133117 |
| 220 | 0,135708 |
| 221 | 0,138332 |
| 222 | 0,140989 |
| 223 | 0,143679 |
| 224 | 0,146403 |
| 225 | 0,149160 |
| 226 | 0,151950 |
| 227 | 0,154774 |
| 228 | 0,157632 |
| 229 | 0,160522 |
| 230 | 0,163447 |
| 231 | 0,166405 |
| 232 | 0,169396 |
| 233 | 0,172421 |
| 234 | 0,175480 |
| 235 | 0,178572 |
| 236 | 0,181698 |
| 237 | 0,184857 |
| 238 | 0,188049 |
| 239 | 0,191275 |
| 240 | 0,194534 |
| 241 | 0,197827 |
| 242 | 0,201152 |
| 243 | 0,204511 |
| 244 | 0,207902 |
| 245 | 0,211327 |
| 246 | 0,214784 |
| 247 | 0,218274 |
| 248 | 0,221796 |
| 249 | 0,225351 |
| 250 | 0,228937 |
| 251 | 0,232556 |
| 252 | 0,236207 |
| 253 | 0,239889 |
| 254 | 0,243603 |
| 255 | 0,247348 |
| 256 | 0,251124 |
| 257 | 0,254931 |
| 258 | 0,258768 |
| 259 | 0,262636 |
| 260 | 0,266534 |
| 261 | 0,270462 |
| 262 | 0,274419 |
| 263 | 0,278406 |
| 264 | 0,282422 |
| 265 | 0,286466 |
| 266 | 0,290539 |
| 267 | 0,294639 |
| 268 | 0,298768 |
| 269 | 0,302924 |
| 270 | 0,307106 |
| 271 | 0,311316 |
| 272 | 0,315551 |
| 273 | 0,319813 |
| 274 | 0,324100 |
| 275 | 0,328412 |
| 276 | 0,332749 |
| 277 | 0,337110 |
| 278 | 0,341495 |
| 279 | 0,345903 |
| 280 | 0,350334 |
| 281 | 0,354788 |
| 282 | 0,359264 |
| 283 | 0,363761 |
| 284 | 0,368279 |
| 285 | 0,372818 |
| 286 | 0,377376 |
| 287 | 0,381955 |
| 288 | 0,386552 |
| 289 | 0,391167 |
| 290 | 0,395801 |
| 291 | 0,400452 |
| 292 | 0,405119 |
| 293 | 0,409803 |
| 294 | 0,414503 |
| 295 | 0,419217 |
| 296 | 0,423946 |
| 297 | 0,428689 |
| 298 | 0,433445 |
| 299 | 0,438214 |
| 300 | 0,442995 |
| 301 | 0,447787 |
| 302 | 0,452590 |
| 303 | 0,457403 |
| 304 | 0,462226 |
| 305 | 0,467057 |
| 306 | 0,471897 |
| 307 | 0,476744 |
| 308 | 0,481599 |
| 309 | 0,486459 |
| 310 | 0,491325 |
| 311 | 0,496196 |
| 312 | 0,501070 |
| 313 | 0,505949 |
| 314 | 0,510830 |
| 315 | 0,515713 |
| 316 | 0,520598 |
| 317 | 0,525483 |
| 318 | 0,530369 |
| 319 | 0,535253 |
| 320 | 0,540137 |
| 321 | 0,545018 |
| 322 | 0,549896 |
| 323 | 0,554771 |
| 324 | 0,559642 |
| 325 | 0,564507 |
| 326 | 0,569367 |
| 327 | 0,574221 |
| 328 | 0.579067 |
| 329 | 0,583906 |
| 330 | 0,588736 |
| 331 | 0,593557 |
| 332 | 0,598368 |
| 333 | 0,603169 |
| 334 | 0,607958 |
| 335 | 0,612735 |
| 336 | 0,617500 |
| 337 | 0,622251 |
| 338 | 0,626988 |
| 339 | 0,631710 |
| 340 | 0,636417 |
| 341 | 0,641107 |
| 342 | 0,645781 |
| 343 | 0,650437 |
| 344 | 0,655075 |
| 345 | 0,659695 |
| 346 | 0,664295 |
| 347 | 0,668875 |
| 348 | 0,673434 |
| 349 | 0,677972 |
| 350 | 0,682488 |
| 351 | 0,686981 |
| 352 | 0,691451 |
| 353 | 0,695897 |
| 354 | 0,700319 |
| 355 | 0,704716 |
| 356 | 0,709088 |
| 357 | 0,713433 |
| 358 | 0,717752 |
| 359 | 0,722043 |
| 360 | 0,726307 |
| 361 | 0,730543 |
| 362 | 0,734750 |
| 363 | 0,738927 |
| 364 | 0,743075 |
| 365 | 0,747193 |
| 366 | 0,751279 |
| 367 | 0,755335 |
| 368 | 0,759359 |
| 369 | 0,763351 |
| 370 | 0,767310 |
| 371 | 0,771237 |
| 372 | 0,775130 |
| 373 | 0,778990 |
| 374 | 0,782815 |
| 375 | 0,786606 |
| 376 | 0,790363 |
| 377 | 0,794084 |
| 378 | 0,797770 |
| 379 | 0,801420 |
| 380 | 0,805034 |
| 381 | 0,808611 |
| 382 | 0,812152 |
| 383 | 0,815656 |
| 384 | 0,819123 |
| 385 | 0,822553 |
| 386 | 0,825945 |
| 387 | 0,829300 |
| 388 | 0,832616 |
| 389 | 0,835895 |
| 390 | 0,839135 |
| 391 | 0,842336 |
| 392 | 0,845499 |
| 393 | 0,848624 |
| 394 | 0,851709 |
| 395 | 0,854756 |
| 396 | 0,857764 |
| 397 | 0,860733 |
| 398 | 0,863663 |
| 399 | 0,866553 |
| 400 | 0,869405 |
| 401 | 0,872217 |
| 402 | 0,874990 |
| 403 | 0,877724 |
| 404 | 0,880419 |
| 405 | 0,883075 |
| 406 | 0,885692 |
| 407 | 0,888269 |
| 408 | 0,890808 |
| 409 | 0,893309 |
| 410 | 0,895770 |
| 411 | 0,898193 |
| 412 | 0,900578 |
| 413 | 0,902924 |
| 414 | 0,905232 |
| 415 | 0,907502 |
| 416 | 0,909734 |
| 417 | 0,911929 |
| 418 | 0,914086 |
| 419 | 0,916205 |
| 420 | 0,918288 |
| 421 | 0,920334 |
| 422 | 0,922344 |
| 423 | 0,924317 |
| 424 | 0,926254 |
| 425 | 0,928155 |
| 426 | 0,930020 |
| 427 | 0,931851 |
| 428 | 0,933646 |
| 429 | 0,935406 |
| 430 | 0,937133 |
| 431 | 0,938825 |
| 432 | 0,940483 |
| 433 | 0,942108 |
| 434 | 0,943699 |
| 435 | 0,945258 |
| 436 | 0,946785 |
| 437 | 0,948279 |
| 438 | 0,949741 |
| 439 | 0.951173 |
| 440 | 0,952573 |
| 441 | 0,953942 |
| 442 | 0,955281 |
| 443 | 0,956590 |
| 444 | 0,957870 |
| 445 | 0,959120 |
| 446 | 0,960342 |
| 447 | 0,961535 |
| 448 | 0,962701 |
| 449 | 0,963838 |
| 450 | 0,964949 |
| 451 | 0,966032 |
| 452 | 0,967090 |
| 453 | 0,968121 |
| 454 | 0,969127 |
| 455 | 0,970107 |
| 456 | 0,971063 |
| 457 | 0,971994 |
| 458 | 0,972902 |
| 459 | 0,973785 |
| 460 | 0,974646 |
| 461 | 0,975484 |
| 462 | 0,976299 |
| 463 | 0,977093 |
| 464 | 0,977865 |
| 465 | 0,978616 |
| 466 | 0,979346 |
| 467 | 0,980056 |
| 468 | 0,980746 |
| 469 | 0,981416 |
| 470 | 0,982067 |
| 471 | 0,982699 |
| 472 | 0,983313 |
| 473 | 0,983909 |
| 474 | 0,984488 |
| 475 | 0,985049 |
| 476 | 0,985593 |
| 477 | 0,986121 |
| 478 | 0,986633 |
| 479 | 0,987128 |
| 480 | 0,987609 |
| 481 | 0,988074 |
| 482 | 0,988525 |
| 483 | 0,988962 |
| 484 | 0,989384 |
| 485 | 0,989793 |
| 486 | 0,990189 |
| 487 | 0,990571 |
| 488 | 0,990941 |
| 489 | 0,991299 |
| 490 | 0,991644 |
| 491 | 0,991978 |
| 492 | 0,992301 |
| 493 | 0,992612 |
| 494 | 0,992913 |
| 495 | 0,993203 |
| 496 | 0,993483 |
| 497 | 0,993753 |
| 498 | 0,994013 |
| 499 | 0,994264 |
| 500 | 0,994506 |
| 501 | 0,994740 |
| 502 | 0,994964 |
| 503 | 0,995180 |
| 504 | 0,995389 |
| 505 | 0,995589 |
| 506 | 0,995782 |
| 507 | 0,995967 |
| 508 | 0,996146 |
| 509 | 0,996317 |
| 510 | 0,996482 |
| 511 | 0,996640 |
| 512 | 0,996793 |
| 513 | 0,996939 |
| 514 | 0,997079 |
| 515 | 0,997213 |
| 516 | 0,997343 |
| 517 | 0,997466 |
| 518 | 0,997585 |
| 519 | 0,997699 |
| 520 | 0,997808 |
| 521 | 0,997913 |
| 522 | 0,998013 |
| 523 | 0,998109 |
| 524 | 0,998200 |
| 525 | 0,998288 |
| 526 | 0,998372 |
| 527 | 0,998452 |
| 528 | 0,998529 |
| 529 | 0,998602 |
| 530 | 0,998673 |
| 531 | 0,998739 |
| 532 | 0,998803 |
| 533 | 0,998864 |
| 534 | 0,998923 |
| 535 | 0,998978 |
| 536 | 0,999031 |
| 537 | 0,999082 |
| 538 | 0,999130 |
| 539 | 0,999176 |
| 540 | 0,999219 |
| 541 | 0,999261 |
| 542 | 0,999301 |
| 543 | 0,999338 |
| 544 | 0,999374 |
| 545 | 0,999408 |
| 546 | 0,999441 |
| 547 | 0,999471 |
| 548 | 0,999501 |
| 549 | 0,999528 |
| 550 | 0.999555 |
| 551 | 0,999580 |
| 552 | 0,999604 |
| 553 | 0,999626 |
| 554 | 0,999648 |
| 555 | 0,999668 |
| 556 | 0,999687 |
| 557 | 0,999705 |
| 558 | 0,999722 |
| 559 | 0,999739 |
| 560 | 0,999754 |
| 561 | 0,999769 |
| 562 | 0,999782 |
| 563 | 0,999795 |
| 564 | 0,999808 |
| 565 | 0,999819 |
| 566 | 0,999830 |
| 567 | 0,999841 |
| 568 | 0,999851 |
| 569 | 0,999860 |
| 570 | 0,999868 |
| 571 | 0,999877 |
| 572 | 0,999884 |
| 573 | 0,999892 |
| 574 | 0,999899 |
| 575 | 0,999905 |
| 576 | 0,999911 |
| 577 | 0,999917 |
| 578 | 0,999922 |
| 579 | 0,999927 |
| 580 | 0,999932 |
| 581 | 0,999936 |
| 582 | 0,999941 |
| 583 | 0,999945 |
| 584 | 0,999948 |
| 585 | 0,999952 |
| 586 | 0,999955 |
| 587 | 0,999958 |
| 588 | 0,999961 |
| 589 | 0,999964 |
| 590 | 0,999966 |
| 591 | 0,999968 |
| 592 | 0,999971 |
| 593 | 0,999973 |
| 594 | 0,999975 |
| 595 | 0,999976 |
| 596 | 0,999978 |
| 597 | 0,999980 |
| 598 | 0,999981 |
| 599 | 0,999982 |
| 600 | 0,999984 |
| 601 | 0,999985 |
| 602 | 0,999986 |
| 603 | 0,999987 |
| 604 | 0,999988 |
| 605 | 0,999989 |
| 606 | 0,999990 |
| 607 | 0,999990 |
| 608 | 0,999991 |
| 609 | 0,999992 |
| 610 | 0,999992 |
| 611 | 0,999993 |
| 612 | 0,999994 |
| 613 | 0,999994 |
| 614 | 0,999994 |
| 615 | 0,999995 |
| 616 | 0,999995 |
| 617 | 0,999996 |
| 618 | 0,999996 |
| 619 | 0,999996 |
| 620 | 0,999997 |
| 621 | 0,999997 |
| 622 | 0,999997 |
| 623 | 0,999997 |
| 624 | 0,999998 |
| 625 | 0,999998 |
| 626 | 0,999998 |
| 627 | 0,999998 |
| 628 | 0,999998 |
| 629 | 0,999998 |
| 630 | 0,999999 |
| 631 | 0,999999 |
| 632 | 0,999999 |
| 633 | 0,999999 |
| 634 | 0,999999 |
Digamos que um crupiê tenha fichas de todos os valores divisíveis por $1. Você entra na mesa com $10. De quantas maneiras diferentes o crupiê pode dar o troco para os $10? E para outros valores de entrada?
Existem 42 maneiras pelas quais o vendedor pode dividir US$ 10. Aqui estão elas:
9,1
8,2
8,1,1
7,3
7,2,1
7,1,1,1
6,4
6,3,1
6,2,2
6,2,1,1
6,1,1,1,1
5,5
5,4,1
5,3,2
5,3,1,1
5,2,2,1
5,2,1,1,1
5,1,1,1,1,1
4,4,2
4,4,1,1
4,3,3
4,3,2,1
4,3,1,1,1
4,2,2,2
4,2,2,1,1
4,2,1,1,1,1
4,1,1,1,1,1,1
3,3,3,1
3,3,2,2
3,3,2,1,1
3,3,1,1,1,1
3,2,2,2,1
3,2,2,1,1,1
3,2,1,1,1,1,1
3,1,1,1,1,1,1,1
2,2,2,2,2
2,2,2,2,1,1
2,2,2,1,1,1,1
2,2,1,1,1,1,1,1
2,1,1,1,1,1,1,1,1
1,1,1,1,1,1,1,1,1,1
Os matemáticos chamam isso de partições. Aqui está o número de partições para quantidades iniciais até 405, que é o máximo que meu computador consegue calcular (2^64).
Aniversário em comum para 2 ou mais pessoas
<!--/box-title-->| Inicial Quantidade | Total Partições |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 5 |
| 5 | 7 |
| 6 | 11 |
| 7 | 15 |
| 8 | 22 |
| 9 | 30 |
| 10 | 42 |
| 11 | 56 |
| 12 | 77 |
| 13 | 101 |
| 14 | 135 |
| 15 | 176 |
| 16 | 231 |
| 17 | 297 |
| 18 | 385 |
| 19 | 490 |
| 20 | 627 |
| 21 | 792 |
| 22 | 1002 |
| 23 | 1255 |
| 24 | 1575 |
| 25 | 1958 |
| 26 | 2436 |
| 27 | 3010 |
| 28 | 3718 |
| 29 | 4565 |
| 30 | 5604 |
| 31 | 6842 |
| 32 | 8349 |
| 33 | 10143 |
| 34 | 12310 |
| 35 | 14883 |
| 36 | 17977 |
| 37 | 21637 |
| 38 | 26015 |
| 39 | 31185 |
| 40 | 37338 |
| 41 | 44583 |
| 42 | 53174 |
| 43 | 63261 |
| 44 | 75175 |
| 45 | 89134 |
| 46 | 105558 |
| 47 | 124754 |
| 48 | 147273 |
| 49 | 173525 |
| 50 | 204226 |
| 51 | 239943 |
| 52 | 281589 |
| 53 | 329931 |
| 54 | 386155 |
| 55 | 451276 |
| 56 | 526823 |
| 57 | 614154 |
| 58 | 715220 |
| 59 | 831820 |
| 60 | 966467 |
| 61 | 1121505 |
| 62 | 1300156 |
| 63 | 1505499 |
| 64 | 1741630 |
| 65 | 2012558 |
| 66 | 2323520 |
| 67 | 2679689 |
| 68 | 3087735 |
| 69 | 3554345 |
| 70 | 4087968 |
| 71 | 4697205 |
| 72 | 5392783 |
| 73 | 6185689 |
| 74 | 7089500 |
| 75 | 8118264 |
| 76 | 9289091 |
| 77 | 10619863 |
| 78 | 12132164 |
| 79 | 13848650 |
| 80 | 15796476 |
| 81 | 18004327 |
| 82 | 20506255 |
| 83 | 23338469 |
| 84 | 26543660 |
| 85 | 30167357 |
| 86 | 34262962 |
| 87 | 38887673 |
| 88 | 44108109 |
| 89 | 49995925 |
| 90 | 56634173 |
| 91 | 64112359 |
| 92 | 72533807 |
| 93 | 82010177 |
| 94 | 92669720 |
| 95 | 104651419 |
| 96 | 118114304 |
| 97 | 133230930 |
| 98 | 150198136 |
| 99 | 169229875 |
| 100 | 190569292 |
| 101 | 214481126 |
| 102 | 241265379 |
| 103 | 271248950 |
| 104 | 304801365 |
| 105 | 342325709 |
| 106 | 384276336 |
| 107 | 431149389 |
| 108 | 483502844 |
| 109 | 541946240 |
| 110 | 607163746 |
| 111 | 679903203 |
| 112 | 761002156 |
| 113 | 851376628 |
| 114 | 952050665 |
| 115 | 1064144451 |
| 116 | 1188908248 |
| 117 | 1327710076 |
| 118 | 1482074143 |
| 119 | 1653668665 |
| 120 | 1844349560 |
| 121 | 2056148051 |
| 122 | 2291320912 |
| 123 | 2552338241 |
| 124 | 2841940500 |
| 125 | 3163127352 |
| 126 | 3519222692 |
| 127 | 3913864295 |
| 128 | 4351078600 |
| 129 | 4835271870 |
| 130 | 5371315400 |
| 131 | 5964539504 |
| 132 | 6620830889 |
| 133 | 7346629512 |
| 134 | 8149040695 |
| 135 | 9035836076 |
| 136 | 10015581680 |
| 137 | 11097645016 |
| 138 | 12292341831 |
| 139 | 13610949895 |
| 140 | 15065878135 |
| 141 | 16670689208 |
| 142 | 18440293320 |
| 143 | 20390982757 |
| 144 | 22540654445 |
| 145 | 24908858009 |
| 146 | 27517052599 |
| 147 | 30388671978 |
| 148 | 33549419497 |
| 149 | 37027355200 |
| 150 | 40853235313 |
| 151 | 45060624582 |
| 152 | 49686288421 |
| 153 | 54770336324 |
| 154 | 60356673280 |
| 155 | 66493182097 |
| 156 | 73232243759 |
| 157 | 80630964769 |
| 158 | 88751778802 |
| 159 | 97662728555 |
| 160 | 107438159466 |
| 161 | 118159068427 |
| 162 | 129913904637 |
| 163 | 142798995930 |
| 164 | 156919475295 |
| 165 | 172389800255 |
| 166 | 189334822579 |
| 167 | 207890420102 |
| 168 | 228204732751 |
| 169 | 250438925115 |
| 170 | 274768617130 |
| 171 | 301384802048 |
| 172 | 330495499613 |
| 173 | 362326859895 |
| 174 | 397125074750 |
| 175 | 435157697830 |
| 176 | 476715857290 |
| 177 | 522115831195 |
| 178 | 571701605655 |
| 179 | 625846753120 |
| 180 | 684957390936 |
| 181 | 749474411781 |
| 182 | 819876908323 |
| 183 | 896684817527 |
| 184 | 980462880430 |
| 185 | 1071823774337 |
| 186 | 1171432692373 |
| 187 | 1280011042268 |
| 188 | 1398341745571 |
| 189 | 1527273599625 |
| 190 | 1667727404093 |
| 191 | 1820701100652 |
| 192 | 1987276856363 |
| 193 | 2168627105469 |
| 194 | 2366022741845 |
| 195 | 2580840212973 |
| 196 | 2814570987591 |
| 197 | 3068829878530 |
| 198 | 3345365983698 |
| 199 | 3646072432125 |
| 200 | 3972999029388 |
| 201 | 4328363658647 |
| 202 | 4714566886083 |
| 203 | 5134205287973 |
| 204 | 5590088317495 |
| 205 | 6085253859260 |
| 206 | 6622987708040 |
| 207 | 7206841706490 |
| 208 | 7840656226137 |
| 209 | 8528581302375 |
| 210 | 9275102575355 |
| 211 | 10085065885767 |
| 212 | 10963707205259 |
| 213 | 11916681236278 |
| 214 | 12950095925895 |
| 215 | 14070545699287 |
| 216 | 15285151248481 |
| 217 | 16601598107914 |
| 218 | 18028182516671 |
| 219 | 19573856161145 |
| 220 | 21248279009367 |
| 221 | 23061871173849 |
| 222 | 25025873760111 |
| 223 | 27152408925615 |
| 224 | 29454549941750 |
| 225 | 31946390696157 |
| 226 | 34643126322519 |
| 227 | 37561133582570 |
| 228 | 40718063627362 |
| 229 | 44132934884255 |
| 230 | 47826239745920 |
| 231 | 51820051838712 |
| 232 | 56138148670947 |
| 233 | 60806135438329 |
| 234 | 65851585970275 |
| 235 | 71304185514919 |
| 236 | 77195892663512 |
| 237 | 83561103925871 |
| 238 | 90436839668817 |
| 239 | 97862933703585 |
| 240 | 105882246722733 |
| 114540884553038 | |
| 242 | 123888443077259 |
| 243 | 133978259344888 |
| 244 | 144867692496445 |
| 245 | 156618412527946 |
| 246 | 169296722391554 |
| 247 | 182973889854026 |
| 248 | 197726516681672 |
| 249 | 213636919820625 |
| 250 | 230793554364681 |
| 251 | 249291451168559 |
| 252 | 269232701252579 |
| 253 | 290726957916112 |
| 254 | 313891991306665 |
| 255 | 338854264248680 |
| 256 | 365749566870782 |
| 257 | 394723676655357 |
| 258 | 425933084409356 |
| 259 | 459545750448675 |
| 260 | 495741934760846 |
| 261 | 534715062908609 |
| 262 | 576672674947168 |
| 263 | 621837416509615 |
| 264 | 670448123060170 |
| 265 | 722760953690372 |
| 266 | 779050629562167 |
| 267 | 839611730366814 |
| 268 | 904760108316360 |
| 269 | 974834369944625 |
| 270 | 1050197489931117 |
| 271 | 1131238503938606 |
| 272 | 1218374349844333 |
| 273 | 1312051800816215 |
| 274 | 1412749565173450 |
| 275 | 1520980492851175 |
| 276 | 1637293969337171 |
| 277 | 1762278433057269 |
| 278 | 1896564103591584 |
| 279 | 2040825852575075 |
| 280 | 2195786311682516 |
| 281 | 2362219145337711 |
| 282 | 2540952590045698 |
| 283 | 2732873183547535 |
| 284 | 2938929793929555 |
| 285 | 3160137867148997 |
| 286 | 3397584011986773 |
| 287 | 3652430836071053 |
| 288 | 3925922161489422 |
| 289 | 4219388528587095 |
| 290 | 4534253126900886 |
| 291 | 4872038056472084 |
| 292 | 5234371069753672 |
| 293 | 5622992691950605 |
| 294 | 6039763882095515 |
| 295 | 6486674127079088 |
| 296 | 6965850144195831 |
| 297 | 7479565078510584 |
| 298 | 8030248384943040 |
| 299 | 8620496275465025 |
| 300 | 9253082936723602 |
| 301 | 9930972392403501 |
| 302 | 10657331232548839 |
| 303 | 11435542077822104 |
| 304 | 12269218019229465 |
| 305 | 13162217895057704 |
| 306 | 14118662665280005 |
| 307 | 15142952738857194 |
| 308 | 16239786535829663 |
| 309 | 17414180133147295 |
| 310 | 18671488299600364 |
| 311 | 20017426762576945 |
| 312 | 21458096037352891 |
| 313 | 23000006655487337 |
| 314 | 24650106150830490 |
| 315 | 26415807633566326 |
| 316 | 28305020340996003 |
| 317 | 30326181989842964 |
| 318 | 32488293351466654 |
| 319 | 34800954869440830 |
| 320 | 37274405776748077 |
| 321 | 39919565526999991 |
| 322 | 42748078035954696 |
| 323 | 45772358543578028 |
| 324 | 49005643635237875 |
| 325 | 52462044228828641 |
| 326 | 56156602112874289 |
| 327 | 60105349839666544 |
| 328 | 64325374609114550 |
| 329 | 68834885946073850 |
| 330 | 73653287861850339 |
| 331 | 78801255302666615 |
| 332 | 84300815636225119 |
| 333 | 90175434980549623 |
| 334 | 96450110192202760 |
| 335 | 103151466321735325 |
| 336 | 110307860425292772 |
| 337 | 117949491546113972 |
| 338 | 126108517833796355 |
| 339 | 134819180623301520 |
| 340 | 144117936527873832 |
| 341 | 154043597379576030 |
| 342 | 164637479165761044d> |
| 343 | 175943559810422753 |
| 344 | 188008647052292980 |
| 345 | 200882556287683159 |
| 346 | 214618299743286299 |
| 347 | 229272286871217150 |
| 348 | 244904537455382406 |
| 349 | 261578907351144125 |
| 350 | 279363328483702152 |
| 351 | 298330063062758076 |
| 352 | 318555973788329084 |
| 353 | 340122810048577428 |
| 354 | 363117512048110005 |
| 355 | 387632532919029223 |
| 356 | 413766180933342362 |
| 357 | 441622981929358437 |
| 358 | 471314064268398780 |
| 359 | 502957566506000020 |
| 360 | 536679070310691121 |
| 361 | 572612058898037559 |
| 362 | 610898403751884101 |
| 363 | 651688879997206959 |
| 364 | 695143713458946040 |
| 365 | 741433159884081684 |
| 366 | 790738119649411319 |
| 367 | 843250788562528427 |
| 368 | 899175348396088349 |
| 369 | 958728697912338045 |
| 370 | 1022141228367345362 |
| 371 | 1089657644424399782 |
| 372 | 1161537834849962850 |
| 373 | 1238057794119125085 |
| 374 | 1319510599727473500 |
| 375 | 1406207446561484054 |
| 376 | 1498478743590581081 |
| 377 | 1596675274490756791 |
| 378 | 1701169427975813525 |
| 379 | 1812356499739472950 |
| 380 | 1930656072350465812 |
| 381 | 2056513475336633805 |
| 382 | 2190401332423765131 |
| 383 | 2332821198543892336 |
| 384 | 2484305294265418180 |
| 385 | 2645418340688763701 |
| 386 | 2816759503217942792 |
| 387 | 2998964447736452194 |
| 388 | 3192707518433532826 |
| 389 | 3398704041358160275 |
| 390 | 3617712763867604423 |
| 391 | 3850538434667429186 |
| 392 | 4098034535626594791 |
| 393 | 4361106170762284114 |
| 394 | 4640713124699623515 |
| 395 | 4937873096788191655 |
| 396 | 5253665124416975163 |
| 397 | 5589233202595404488 |
| 398 | 5945790114707874597 |
| 399 | 6324621482504294325 |
| 400 | 6727090051741041926 |
| 401 | 7154640222653942321 |
| 402 | 7608802843339879269 |
| 403 | 8091200276484465581 |
| 404 | 8603551759348655060 |
| 405 | 9147679068859117602 |
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
Como perguntado no filme Meninas Malvadas , o que é:
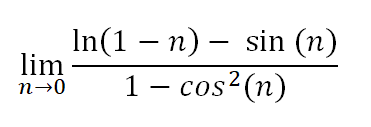
Vamos começar observando um gráfico de n (eixo x) por f(n) (eixo y).
Como você pode ver, o limite tende a ∞ pela esquerda e a -∞ pela direita. Como a reta não converge para o mesmo lugar por ambos os lados, não há limite.
No entanto, vamos responder à pergunta sem usar um gráfico. A regra de L'Hôpital diz que se o limite de f(x)/g(x) = 0/0, então lim f(x)/g(x) = lim f'(x)/g'(x). Portanto, vamos resolver para f'(x) e g'(x).
f'(n) = ((ln(1-n) - sin(n)) d/dn = -1/(1-n) - cos(n)
g'(n) = (1 - cos² (n)) d/dn = sin² (n) d/dn
Vamos usar a regra do produto para resolver sin² (n) d/dn
pecado 2 (n) d/dn = pecado (n) × pecado (n) d/dn =
sen(n) × cos(n) + cos(n) × sen(n) =
2sen(n)cos(n).
Em seguida, vamos resolver para f'(n) e g'(n) em n = 0.
f'(0) = -1/(1-0) - cos(0) = -2.
g'(0) = 2sen(0)cos(0) = 0
Portanto, f'(0)/g'(0) = -2/0 = -∞. Assim, o limite da função original não existe.

Gostaria de parabenizar os roteiristas de Meninas Malvadas por terem acertado em cheio na matemática do filme. Até mesmo filmes que abordam matemática de forma séria, como Gênio Indomável, muitas vezes erram feio nos cálculos.
No episódio 4 da 3ª temporada de Young Sheldon, intitulado "Hobbitses, Physicses and a Ball With Zip" , Sheldon se pergunta quantas combinações são possíveis em uma cartela de bingo. Qual é a resposta e as fórmulas mostradas na série estão corretas?
Primeiro, vou analisar o número de permutações. Isso significa que não apenas os números importam, mas também a ordem deles na cartela. Existem permut(15,5) = 15!/(15-5)! = 15*14*13*12*11 = 360.360 permutações possíveis para as colunas B, I, G e O. Para a coluna N, o número de permutações é permut(14,4) = 15!/(15-4)! = 15*14*13*12 = 32.760. Portanto, o número total de permutações de cartelas de bingo é 360.360 × 4 × 32.760 = 552.446.474.061.128.648.601.600.000.
Em segundo lugar, vou analisar o número de combinações. Isso significa que os números importam, mas não a ordem deles na cartela. Existem combin(15,5) = 15!/(5!*(15-5)!) = (15*14*13*12*11)/(1*2*3*4*5) = 3.003 combinações possíveis para as colunas B, I, G e O. Para a coluna N, o número de permutações é combin(14,4) = 15!/(4!*(15-4)!) = (15*14*13*12)/(1*2*3*4) = 1.365. Portanto, o número total de permutações de cartelas de bingo é 3.003 × 4 × 1.365 = 111007923832370565.
No episódio, Sheldon se pergunta quantas cartelas de bingo ÚNICAS podem existir. Com base nas fórmulas incorretas que ele usa posteriormente, presumo que ele esteja se referindo a permutações. Em outras palavras, duas cartelas com os mesmos números, mas em posições diferentes, seriam ambas únicas.
A imagem acima mostra a fórmula de Sheldon para as colunas B, I, G e O. Inicialmente, ele acerta a fórmula com 5! × combin(15,5). No entanto, ele a simplifica incorretamente para 15!/(15!-5)!. O segundo ponto de exclamação não deveria estar lá. Deveria ser 15!/(15-10)!. Contudo, ele retorna à resposta correta em 360,360.

Temos exatamente o mesmo problema com a coluna N. A fórmula deveria ser 15!/(15-4)!, e não 15!/(15!-4)!. O segundo ponto de exclamação estraga tudo.
O irônico é que, mais tarde no episódio, Sheldon fica obcecado com os erros na cronologia de O Senhor dos Anéis, assim como eu estou obcecado com isso.

Há um tanque cheio de 100 litros contendo água e 10 kg de sal. Se adicionarmos 10 litros de água pura por minuto, enquanto simultaneamente esvaziamos 10 litros da solução por minuto, quanto sal restará no tanque após 30 minutos?
Vamos começar definindo algumas variáveis:
- s = kg de sal no tanque
- t = minutos desde que o sal foi adicionado ao tanque
Sabemos que 10% do sal é drenado por minuto. Em termos matemáticos:
ds/dt = (-10/100) × s
Vamos reorganizar isso para:
ds = (-10/100) × s dt
-10/s ds = dt
Integrando ambos os lados:
(1) -10×ln(s) = t + c
Em seguida, vamos encontrar a temida constante de integração. Para isso, sabemos que s = 10 quando t = 0. Substituindo esse valor na fórmula (1) acima, obtemos:
-10 × ln(10) = 0 + c
Então c = -10×ln(10)
Substituindo isso na equação (1), obtemos:
(2) -10×ln(s) = t -10×ln(10)
A questão em análise é a quantidade de sal no tanque em t=30. Resolvendo para s quando t=30:
-10×ln(s) = 30 -10×ln(10). Em seguida, divida ambos os lados por -10...
ln(s) = -3 + ln(10)
s = exp(-3 + ln(10))
s = exp(-3) × exp(ln(10))
s = exp(-3) × 10
s =~ 0,4979 kg de sal.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Dado que a figura maior é um quadrado, qual é a área de x?
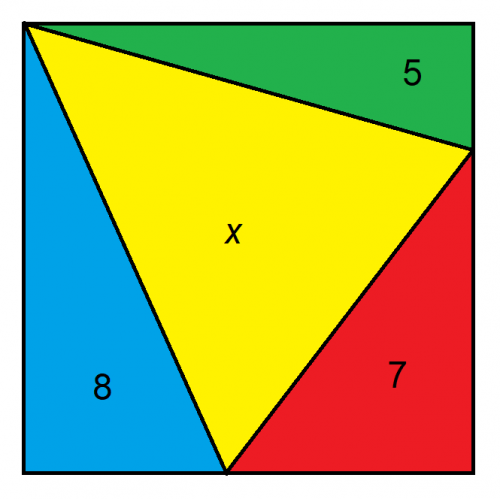
A chave para problemas como este está na sua formulação. Recomendo tentar simplificar o problema ao máximo possível, reduzindo-o ao mínimo de incógnitas. Neste caso, podemos expressar as distâncias desconhecidas no quadrado em apenas três, da seguinte forma:
É mais fácil lidar com retângulos do que com triângulos. Dado que sabemos a área de três triângulos, podemos dobrar o tamanho e dobrar as áreas. Isso nos dá:
- ab=10
- ac=16
- (ab)(ac)=14
Vamos fatorar (ab)(ac):
a² - ab - ac + bc = 14
a 2 - 10 - 16 + bc = 14
(1) a² + bc = 40
Vamos expressar b e c em termos de a, para reduzir isso a uma única variável:
b = 10/a
c = 16/a
Substituindo esses valores para b e c na equação (1):
a² + (10/a)*(16/a) = 40
a² + 160/ a² = 18
Em seguida, vamos eliminar esse 2 do denominador multiplicando tudo por 2 .
a⁴ + 160 = 40* a²
a₄ - 40* a₂ + 160 = 0
Vamos definir uma nova variável y = a 2
y² - 18y + 32 = 0
Em seguida, vamos resolver para y usando a fórmula quadrática:
y = (40 +/- sqrt(1600-640))/2
y = (40 +/- sqrt(960))/2
y = (40 +/- 8*sqrt(15))/2
y = 20 +/- 4*sqrt(15)
A área do quadrado inteiro é a 2 , que convenientemente é igual a y. Da equação acima, se o +/- for negativo, então y = apx 4,5081, o que está obviamente errado, já que sabemos que a área é pelo menos 20, sem nem mesmo incluir x. Portanto, a área do quadrado deve ser 20 + 4*sqrt(15).
Os três triângulos que nos foram dados têm uma área de 5+7+8=20. Subtraindo isso da área total do quadrado, obtemos a área de x: 20 + 4*sqrt(15) - 20 = 4*sqrt(15) = aproximadamente 15,4919.
Essa questão é levantada e discutida no meu fórum no Wizard of Vegas .

Reparem na minha camiseta nesta foto. A caixa do cinema elogiou-a quando fui ver "Uncut Gems" . Agradeci-lhe torturando-a com este problema, só que com triângulos de áreas 2, 3 e 4. Depois do filme, fui ver como ela estava e ela ainda não tinha resolvido, mas parecia estar a tentar. Então, escrevi a seguinte solução para ela no bar Suncoast. Ela pareceu gostar bastante. Acho que essa jovem vai longe na vida.
Há um alvo de dardos quadrado de dimensões 1 por 1. Um dardo é lançado contra ele de forma que pode atingir qualquer ponto com igual probabilidade. Sejam as coordenadas do ponto de impacto (x, y), onde x e y são uniformemente e independentemente distribuídos entre 0 e 1.
Seja z = arredondar(x/y). Em outras palavras, z = x/y, arredondado para o inteiro mais próximo. Qual é a probabilidade de z ser par?
Será muito útil conhecer a série infinita na dica a seguir.
A fórmula de Leibniz para π afirma:
1/1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... = π/4
Para obter apenas a resposta, clique no botão a seguir.
Clique no botão abaixo para ver a solução.
Se x/y < 0,5, então a razão será arredondada para baixo, resultando em 0, um número par. Qualquer ponto no alvo de dardos à esquerda da linha formada por (0,0) e (0,5) será arredondado para baixo, resultando em 0. Essa área é um triângulo retângulo com lados de 1 e 1/2. Lembre-se que a área de um triângulo é (1/2) * base * altura. Portanto, a área desses pontos, arredondando para baixo, resulta em (1/2) * (1/2) = 1/4.
A próxima área no gráfico que será arredondada para o próximo número par, 2, é quando 1,5 < x/y < 2,5. Essa área será um triângulo com base 2/3 - 2/5 e altura 1. Observe que esses são os inversos dos limites de x/y, porque x é igual a 1, então precisamos inverter y. Portanto, a área que arredonda para 2 é (1/2)*(2/3 - 2/5).
A próxima área no gráfico que será arredondada para o próximo número par, 4, é quando 3,5 < x/y < 4,5. Esta área será um triângulo com base 2/7 - 2/9 e altura 1. Portanto, a área que arredonda para 2 é (1/2)*(2/7 - 2/9).
A próxima área no gráfico que será arredondada para o próximo número par, 6, é quando 5,5 < x/y < 6,5. Esta área será um triângulo com base 2/11 - 2/13 e altura 1. Portanto, a área que arredonda para 2 é (1/2)*(2/11 - 2/13).
Começando a perceber um padrão? É o seguinte:
1/4 + 1/2*(2/3 - 2/5 + 2/7 - 2/9 + 2/11 - 2/13 + ... ) =
1/4 + (1/3 - 1/5 + 1/7 - 1/9 + 1/11 - 1/13 + ... ) =
Vamos colocar um -1 dentro desses parênteses.
5/4 + (-1 + 1/3 - 1/5 + 1/7 - 1/9 + 1/11 - 1/13 + ... ) =
5/4 - (1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + 1/13 + ... ) =
Em seguida, relembre nossa dica acima:
1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11
Voltando à questão em pauta...
5/4 - π/4 =
(5 - π) / 4 = apx. 0,464601836602552.
É interessante como π e e continuam aparecendo em vários lugares na matemática.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Seja 9x + 12x = 16x
Qual é o valor de x?
Clique no botão abaixo para ver a resposta.
Clique no botão abaixo para ver a solução.
9x + 12x = 16x =
Divida ambos os lados por 9 x
1 + (12/9) x = (16/9) x
1 + (4/3) x = ((4/3) x ) 2
(1) Seja u = (4/3) x
1 + u = u 2
Pela fórmula quadrática...
u = (1+sqrt(5)) / 2 (A Proporção Áurea)
Colocando isso de volta na equação (1):
(4/3) x = (1+sqrt(5)) / 2
Calcule o logaritmo de ambos os lados:
x ln(4/3) = ln[(1+sqrt(5)) / 2]
x = ln[(1+sqrt(5)) / 2] / ln(4/3)
x = [ln(1+sqrt(5) - ln(2)] / [ln(4) - ln(3)] = aproximadamente 1,67272093446233.
Essa questão é levantada e discutida no meu fórum no Wizard of Vegas .
Agradecimento: Obtive uma variação deste problema de Presh Talwalkar, da Mind Your Decisions .
Um agricultor planta 5 sementes de maçã. A cada dia, cada semente terá 1/3 de chance de germinar. Qual é o tempo médio até que todas as cinco árvores germinem?
Um agricultor planta 5 sementes de maçã. A cada dia, cada semente terá 1/3 de chance de germinar. Qual é o tempo médio até que todas as cinco árvores germinem?
Vamos calcular de trás para frente. Se houver uma única semente que ainda não germinou, ela levará em média 1/p dias para germinar, onde p é a probabilidade de germinar em um determinado dia. Como p = 1/3, levará em média 3 dias para germinar. Vamos chamar esse tempo de t₁ = 3.
E se restarem duas sementes? Há uma probabilidade de ap² = 1/9 de que ambas germinem no dia seguinte e o processo termine. A probabilidade de uma delas germinar no dia seguinte é 2 × p × q, onde q é a probabilidade de não germinar. Assim, a probabilidade de uma semente germinar é 2 × (1/3)(2/3) = 4/9. A probabilidade de nenhuma das sementes germinar é q² = (2/3) ² = 4/9. Vamos chamar o número esperado de dias com duas sementes de t² .
t 2 = 1 + (4/9)×t 1 + (4/9)t 2
t 2 = (1 - (4/9)) = 1 + (4/9)×t 1
t 2 = (1 + (4/9)×3) / (1 - (4/9))
t 2 = (21/9) / (5/9)
t 2 = (21/9) × (9/5) = 21/5 = 4,2
E se restarem três sementes? Há uma probabilidade de ap³ = 1/27 de que todas germinem no dia seguinte e o experimento termine. A probabilidade de uma germinar no dia seguinte é 3 × p × q² = 3 × (1/3)(2/3) ² = 12/27. A probabilidade de duas germinarem no dia seguinte é 3 × p² × q = 3 × (1/3) ² × (2/3) = 6/27. A probabilidade de nenhuma semente germinar é q³ = (2/3) ³ = 8/27. Vamos chamar o número esperado de dias com três sementes de t³ .
t 3 = 1 + (6/27)t 1 + (12/27)×t 2 + (8/27)×t 3
t 3 = 1 + (6/27)×3 + (12/27)×4,2 + (8/27)×t 3
t 3 × (1 - 8/27) = (1 + 18/27 + 28/15)
t 3 = (1 + 18/27 + 28/15) / (1 - 8/27) = 477/95 = aproximadamente 5,02105263
E se restarem quatro sementes? Há uma probabilidade de ap₄ = 1/81 de que todas as quatro germinem no dia seguinte e o experimento termine. A probabilidade de uma germinar no dia seguinte é 4 × p × q³ = 4 × (1/3)(2/3) ³ = 32/81. A probabilidade de duas germinarem no dia seguinte é combin(4,2) × p² × q² = 6 × (1/3) ² × (2/3) ² = 24/81. A probabilidade de três germinarem no dia seguinte é combin(4,3) × p³ × q = 4 × (1/3) ³ × (2/3) = 8/81. A probabilidade de nenhuma semente germinar é q₄ = (2/3) ⁴ = 16/81. Vamos chamar o número esperado de dias com três sementes de t₄ .
t 4 = 1 + (8/81)×t 1 + (24/81)×t 2 + (32/81)×t 3 + (16/81)×t 4
t 4 = 1 + (8/81)×3 + (24/81)×4,2 + (32/81)×5,02105263 + (16/81)×t 4
t 4 = (1 + (8/81)×3 + (24/81)×4,2 + (32/81)×5,02105263) / (1 - (16/81))
t 4 = aprox. 5,638056680161943319838056680.
E se restarem todas as cinco sementes? Há uma probabilidade de 5 = 1/243 de que todas as 5 germinem no dia seguinte e o experimento termine. A probabilidade de uma germinar no dia seguinte é 5 × p × q⁴ = 5 × (1/3)(2/3) ⁴ = 80/243. A probabilidade de duas germinarem no dia seguinte é combin(5,2) × p² × q³ = 10 × (1/3) ² × (2/3) ³ = 80/243. A probabilidade de três germinarem no dia seguinte é combin(5,3) × p³ × q = 10 × (1/3) ³ × (2/3) ² = 40/243. A probabilidade de quatro germinarem no dia seguinte é combin(5,4)×p 4 ×q = 5×(1/3) 4 ×(2/3) = 10/243. A probabilidade de nenhuma semente germinar é q 5 = (2/3) 5 = 32/243. Vamos chamar o número esperado de dias com três sementes de t 5 .
t 5 = 1 + (10/243)×t 1 + (40/243)×t 2 + (80/81)×t 3 + (80/243)×t 4 + (32/243)×t 5
t 5 = (1 + (10/243)×t 1 + (40/243)×t 2 + (80/81)×t 3 + (80/243)×t 4 ) / (1 - (32/243))
t 5 = (1 + (10/243)×3 + (40/243)×4,2 + (80/243)×(477/95) + (80/243)×5,63805668) / (1 - (32/243))
t 5 = aproximadamente 6,131415853.
Este problema foi adaptado de um problema semelhante criado por Presh Talwalkar, do Mind Your Decisions .
Tenho uma pergunta em duas partes.
Para a parte 1, dado:- x + y + z = 1
- x² + y² + z² = 4
- x^3 + y^3 + z^3 = 9
Qual é o resultado de x^4 + y^4 + z^4?
Na segunda parte, qual é a resposta para o caso geral quando:
- x + y + z = a
- x² + y² + z² = b
- x^3 + y^3 + z^3 = c
Pergunta 1: 97/6 = aproximadamente 16,166666
Questão 2: a⁴ /6 + (4/3)ac - a²b + b² /2
Para ver minha solução (PDF)
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
Um micróbio, que chamaremos de Covid-20, pode gerar um novo micróbio a qualquer momento. A probabilidade de um determinado micróbio gerar um novo micróbio a partir de um micróbio parental específico em um dado momento é sempre a mesma, independentemente do tempo decorrido desde a última geração. O tempo médio entre gerações do mesmo micróbio é de um dia. Em termos matemáticos, o tempo esperado entre gerações do mesmo micróbio segue uma distribuição exponencial com média de um dia.
Uma vez que um micróbio entra nos seus pulmões, qual é o número esperado de micróbios que você terá após sete dias?
Clique no botão abaixo para ver a resposta.
Clique no botão abaixo para ver a solução.
Essa solução exigirá uma equação diferencial ordinária. Se você ainda não chegou a esse ponto em seus estudos de matemática, não conseguirá entendê-la.
Deixar:
m = Número de micróbios da Covid-20
t = tempo, em dias
Como cada micróbio gera, em média, um novo micróbio por dia, m micróbios gerarão, em média, m novos micróbios por dia. Em outras palavras, a taxa de crescimento de micróbios (m) em qualquer instante t pode ser escrita como:
dm/dt = m.
Não tenho certeza da maneira correta de expressar isso, mas separe o dt para o lado direito:
dm = m dt.
Divida ambos os lados por m:
1/m dm = 1 dt.
Integrar ambos os lados:
ln(m) = t + C, onde C é a constante de integração.
Sabemos que no instante t = 0 existe um micróbio. Em outras palavras, quando t = 0, m = 1. Podemos usar esses valores na equação acima para calcular C:
ln(1) = 0 + C
0 = 0 + C
C = 0.
Agora temos ln(m) = t.
Calcule a função exponencial (exp()) de ambos os lados:
m = e t
Assim, no instante t=7, haverá e 7 = aproximadamente 1096,6332 micróbios.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Num antigo saloon do Velho Oeste, uma discussão sobre um jogo de cartas se intensificou, com todos os cowboys presentes sacando suas armas e atirando uns nos outros.
Quando a fumaça finalmente se dissipou, 90% dos cowboys haviam sido baleados na perna, 85% no braço, 80% no abdômen e 75% na cabeça. Surpreendentemente, apenas os cowboys que sofreram os quatro tipos de ferimentos morreram no grande tiroteio.
Qual é a menor porcentagem possível de cowboys que acabaram sendo sepultados?
Primeiro, atire na perna de 90% dos cowboys.
Em seguida, atire nos 10% restantes no braço. Você ainda tem 75% para atirar no braço, então pegue-os dos que já foram atingidos na perna.
Então, agora estamos em:
Apenas 15% das pernas (90% - 75%)
Apenas 10% do braço
Ambos 75%
Nem 0%
Total da perna: 90%
Braço total: 85%
Em seguida, vamos analisar as lesões abdominais (80%). Elimine os 25% com apenas uma lesão abdominal. Temos 80% - 25% = 55% mais pessoas para eliminar. Selecionaremos esses 55% do grupo de pessoas com ambas as lesões. Portanto, agora temos:
Pernas e abdômen 15%
Braço e abdômen 10%
Pernas e braços 20% (75% - 55%)
Todos os três 55%
Uma lesão 0%
Zero lesões 0%
Por fim, considere os 75% com lesões na cabeça. Primeiro, elimine os 45% com exatamente duas lesões. Ainda temos 30% para eliminar, então vamos eliminá-los dos 55% com todas as três lesões. Isso nos deixa com:
Cabeça, perna e intestino 15%
Cabeça, braços e abdômen 10%
Cabeça, perna e braço 20%
Perna, braço e intestino: 25% (55% - 30%)
Todos os quatro 30%
Zero lesões 0%
Uma lesão 0%
Duas lesões 0%
Vamos considerar 20 cowboys. Escolhemos esse número porque todas as probabilidades envolvidas são divisíveis por 5% e 5% de 20 é 1.
Alinhe-os em fila. Em seguida, começando pela esquerda, atire em 90% deles, o que dá 18, na perna. Depois, faça um diagrama com o número do cowboy na linha superior e o total de lesões de cada um na coluna da esquerda, como segue.
| Ferida | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | ||
| 2 | ||||||||||||||||||||
| 3 | ||||||||||||||||||||
| 4 | ||||||||||||||||||||
| Total | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
Em seguida, você precisará acertar 85% dos tiros, ou seja, 17 no braço. Comece com os dois cowboys que não foram atingidos na perna. Você ainda tem mais 15 para acertar. Volte para o cowboy da esquerda e continue descendo a fileira, acertando um total de 15 tiros na perna dos que já foram atingidos. Seu cartão de lesões deve ficar assim:
| Ferida | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | UM | UM |
| 2 | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | |||||
| 3 | ||||||||||||||||||||
| 4 | ||||||||||||||||||||
| Total | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 |
Em seguida, você precisará acertar 80% dos tiros, ou seja, 16 na barriga. Comece com os CINCO cowboys que têm apenas uma lesão. Você ainda tem mais 11 para acertar. Volte para o cowboy à esquerda e continue descendo a fileira, acertando um total de 11 que já foram atingidos duas vezes. Seu cartão de lesões deve ficar assim:
| Ferida | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | UM | UM |
| 2 | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | G | G | G | G | G |
| 3 | G | G | G | G | G | G | G | G | G | G | G | |||||||||
| 4 | ||||||||||||||||||||
| Total | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
Em seguida, você precisará acertar 75% dos tiros, ou seja, 15 tiros na cabeça. Comece com os nove cowboys que já levaram dois tiros. Faltam 6. Volte para o cowboy da esquerda e continue descendo a fileira, acertando um total de 6 cowboys que já levaram três tiros. Seu cartão de ferimentos deve ficar assim:
| Ferida | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | eu | UM | UM |
| 2 | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | UM | G | G | G | G | G |
| 3 | G | G | G | G | G | G | G | G | G | G | G | H | H | H | H | H | H | H | H | H |
| 4 | H | H | H | H | H | H | ||||||||||||||
| Total | 4 | 4 | 4 | 4 | 4 | 4 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
Como você pode ver, 6 cowboys foram baleados quatro vezes e 14 três vezes. Portanto, a porcentagem máxima que pode sofrer apenas três ferimentos é 14/20 = 70%.
Para o caso geral, se as quatro probabilidades forem a, b, c e d, então a proporção máxima que pode sobreviver é 1-(a+b+c+d), desde que a+b+c+d >=3 e a+b+c+d <=4.
Gostaria de agradecer e dar os devidos créditos a CharliePatrick, membro do fórum Wizard of Vegas, por esta solução.
Essa pergunta é feita e discutida no meu fórum, começando com esta postagem .
Um sapo consegue saltar um pé ou dois pés. O sapo salta um total de dez pés exatamente em vários saltos, sempre para a frente. De quantas maneiras diferentes isso pode ser feito, considerando tanto a distância quanto a ordem dos saltos?
- Se o sapo precisa pular apenas um pé, obviamente só há um caminho. Lembre-se, o sapo não pode ultrapassar o alvo.
- Se o sapo precisar pular dois pés, há duas maneiras de fazer isso -- (1) 1 pé e 1 pé, ou (2) 2 pés.
Se o sapo precisa pular três pés, ele pode estar a um pé ou a dois pés de distância antes do salto final. Há uma maneira de estar a dois pés de distância, como mostrado no passo 1, e duas maneiras de estar a um pé de distância, como mostrado no passo 2. Portanto, há três maneiras de pular três pés de distância. Isso também pode ser facilmente verificado como (1) 1+1+1, (2) 1+2, (3) 2+1.
Se o sapo precisa pular quatro pés, ele pode estar a dois pés ou três pés de distância antes do salto final. Há 2 maneiras de estar a 2 pés de distância, como mostrado no passo 2, e 3 maneiras de estar a 1 pé de distância, como mostrado no passo 3. Portanto, há 5 maneiras de pular quatro pés de distância. Isso também pode ser facilmente verificado como (1) 1+1+1+1, (2) 1+1+2, (3) 1+2+1, (4) 2+1+1, (5) 2+2.
Se o sapo precisa pular 5 pés, então ele pode estar a 3 pés ou 4 pés de distância antes do salto final. Existem 3 maneiras de estar a 2 pés de distância, como mostrado no passo 3, e 5 maneiras de estar a 1 pé de distância, como mostrado no passo 4. Assim, existem 3 + 5 = 8 maneiras de pular cinco pés de distância. Isso também pode ser facilmente verificado como (1) 1 + 1 + 1 + 1, (2) 1 + 1 + 1 + 2, (3) 1 + 1 + 2 + 1, (4) 1 + 2 + 1 + 1, (5) 2 + 1 + 1 + 1, (6) 2 + 2 + 1, (7) 2 + 1 + 2, (8) 1 + 2 + 2.
Você começa a perceber um padrão? É a sequência de Fibonacci. Seguindo a mesma lógica, existem 89 maneiras pelas quais o sapo pode pular exatamente dez pés.Usando as moedas padrão dos EUA de 1, 5, 10, 25, 50 centavos e 1 dólar, de quantas maneiras é possível dar troco de 1 dólar?
Seja a(x) = número de maneiras de formar x centavos, usando apenas moedas de um centavo e de cinco centavos, onde x é divisível por 5.
a(x) = 1+(x/5)
Em outras palavras, o número de maneiras é o número de moedas de cinco centavos possíveis no troco, que varia de 0 a x/5.
Seja b(x) = número de maneiras de formar x centavos, usando apenas moedas de um centavo, cinco centavos e dez centavos, onde x é divisível por 5.
b(0)=1
b(5)=2
b(x) = a(x) + b(x-10), onde x>=10.
Em inglês simples, o número de maneiras de fazer x centavos é a soma de (1) b(x-10) = número de maneiras de x-10 centavos adicionando um dime a cada maneira e (2) a(x) = número de maneiras sem usar dimes.
Seja c(x) = número de maneiras de formar x centavos, usando apenas moedas de um centavo, cinco centavos, dez centavos e vinte e cinco centavos, onde x é divisível por 25.
c(0) = 1
c(x) = b(x) + c(x-25), onde x>=25.
Em inglês simples, o número de maneiras de fazer x centavos é a soma de (1) c(x-25) = número de maneiras de x-25 centavos adicionando um quarto de dólar a cada maneira e (2) b(x) = número de maneiras sem usar quartos de dólar.
Seja d(x) = número de maneiras de formar x centavos, usando apenas moedas de um centavo, cinco centavos, dez centavos, vinte e cinco centavos e cinquenta centavos, onde x é divisível por 50.
d(0) = 1
d(x) = c(x) + d(x-50), onde x>=50.
Em inglês simples, o número de maneiras de fazer x centavos é a soma de (1) d(x-50) = número de maneiras de x-50 centavos adicionando meio dólar a cada maneira e (2) c(x) = número de maneiras sem usar meio dólar.
A seguir, encontra-se uma tabela que mostra esses valores para x = 5 a 100.
Formas de promover mudanças
| x | machado) | b(x) | c(x) | d(x) |
|---|---|---|---|---|
| 0 | 1 | 1 | 1 | |
| 5 | 2 | 2 | 0 | |
| 10 | 3 | 4 | 0 | |
| 15 | 4 | 6 | 0 | |
| 20 | 5 | 9 | 0 | |
| 25 | 6 | 12 | 13 | |
| 30 | 7 | 16 | 0 | |
| 35 | 8 | 20 | 0 | |
| 40 | 9 | 25 | 0 | |
| 45 | 10 | 30 | 0 | |
| 50 | 11 | 36 | 49 | 50 |
| 55 | 12 | 42 | 0 | |
| 60 | 13 | 49 | 0 | |
| 65 | 14 | 56 | 0 | |
| 70 | 15 | 64 | 0 | |
| 75 | 16 | 72 | 121 | |
| 80 | 17 | 81 | 0 | |
| 85 | 18 | 90 | 0 | |
| 90 | 19 | 100 | 0 | |
| 95 | 20 | 110 | 0 | |
| 100 | 21 | 121 | 242 | 292 |
Finalmente, adicione um para a moeda de 1 dólar e a resposta é 292 + 1 = 293.
Essa questão é levantada e discutida no meu fórum no Wizard of Vegas .
Há um número infinito de lâmpadas, todas apagadas. O intervalo de tempo entre o momento em que uma lâmpada é acesa segue uma distribuição exponencial* com média de um dia. Uma vez acesa, a vida útil de uma lâmpada também segue uma distribuição exponencial com média de um dia.
Qual é o tempo médio até que a primeira lâmpada queime?
*: Eventos aleatórios que seguem a distribuição exponencial possuem a propriedade de não terem memória, ou seja, o passado não importa. Em outras palavras, um único evento nunca está atrasado e a probabilidade de ele ocorrer é sempre a mesma.
Em média, levará um dia para que a primeira lâmpada seja acesa.
A partir daí, levará em média meio dia até o próximo evento significativo, seja uma nova lâmpada sendo acesa ou a primeira lâmpada queimando. Adicionamos 1/2 dia ao tempo de espera até esse evento. Portanto, agora estamos em 1 + (1/2) = 1,5 dias.
Há 1/2 de chance de o segundo evento ter sido o acendimento de uma segunda lâmpada. Nesse caso, há um tempo de espera de 1/3 de dia até o próximo evento significativo (seja uma das duas primeiras lâmpadas queimando ou uma nova lâmpada sendo acesa). Portanto, somando o produto de 1/2 (a probabilidade de chegar até aqui) e 1/3, que é igual a 1/6, ao tempo de espera, temos 1,5 + 1/6 = 5/3 = 1,66667 dias.
Há uma probabilidade de (1/2)*(1/3) = 1/6 de que o terceiro evento significativo tenha sido o acendimento de uma terceira lâmpada. Nesse caso, há um tempo de espera de 1/4 de dia até o próximo evento significativo (seja uma das três primeiras lâmpadas queimando ou uma nova lâmpada acendendo). Portanto, somando o produto de 1/6 (a probabilidade de chegar até aqui) e 1/4, que é igual a 1/24, ao tempo de espera, temos 5/3 + 1/24 = 41/24 = 1,7083 dias.
Seguindo esse padrão, a resposta é (1/1!) + (1/2!) + (1/3!) + (1/4!) + (1/5!) + ...
Deve ser de conhecimento geral que e = (1/0!) + (1/1!) + (1/2!) + (1/3!) + (1/4!) + (1/5!) + ...
A única diferença é que nossa resposta não inclui o fator 1/0!. Portanto, a resposta é e - 1/0! = e - 1 = aproximadamente 1,7182818...
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
A, B, C e D são todos números inteiros positivos diferentes.
A < B < C < D
Encontre o maior D possível de forma que
1/A + 1/B + 1/C + 1/D = 1
A resposta é 42. A, B e C são 2, 3 e 7.
1/2 + 1/3 + 1/7 + 1/42 = 1.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Depois de assistir a O Gambito da Rainha , notei que nenhuma das partidas na série terminou em empate. Eu pensava que o xadrez em alto nível tivesse muitos empates. Para o xadrez de nível grande mestre, qual a porcentagem de partidas que terminam em empate?
De acordo com o artigo "O número de empates no xadrez aumentou?" no ChessBase.com, o autor Qiyu Zhou afirma que, em 78.468 partidas ranqueadas entre jogadores com rating de 2600 ou superior (são necessários 2500 pontos para ser um grande mestre), os resultados foram os seguintes:
- Vitórias dos negros: 18,0%
- Vitórias dos brancos: 28,9%
- Empate: 53,1%
Há um tabuleiro de pinos 5x5 com 3 pinos. Qual é a probabilidade de que três pinos colocados aleatoriamente formem um triângulo?
Primeiro, existem combin(25,3) = 2.300 combinações possíveis para os pinos.
Quantas dessas combinações formam um triângulo? Vamos usar este tabuleiro para ajudar:
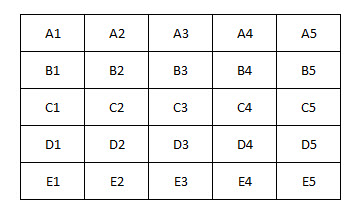
Primeiro, há cinco linhas, cinco colunas e duas diagonais. Para qualquer uma delas, há combin(5,3) = 10 maneiras de colocar os pinos em linha. Portanto, há 12*10 = 120 combinações dessa forma.
Em segundo lugar, existem quatro maneiras de conectar o quadrado central de uma linha/coluna ao quadrado central de uma linha/coluna adjacente. Em outras palavras, essas três posições:
- A3, B4, C5
- C5, D4, E3
- E3, D2, C1
- C1, B2, A3
Então, agora estamos com 120 + 4 = 124.
Terceiro, existem quatro linhas diagonais diferentes que representam quatro espaços:
- Lá2, Si3, Dó4, Ré5
- B5, C4, D3, E2
- E4, D3, C2, B1
- Ré1, Dó2, Si3, Lá4
Para cada um deles existem combin(4,3)=4 maneiras de colocar três pinos. Isso adiciona 4*4 = 16 a mais.
Agora estamos em 124 + 16 = 140
Em quarto lugar, considere a forma como os cavalos se movem no xadrez, num tabuleiro em forma de L de 2x1. Para cada vértice, existem duas maneiras pelas quais um cavalo pode se mover. Em todas elas, o cavalo pode se mover novamente na mesma linha formada pelo primeiro movimento. Portanto, são 4*2 = 8 movimentos adicionais:
- Lá1, Dó2, Mi3 Lá1, Si3, Dó5
- A5, B3, C1
- Lá5, Dó4, Mi3
- E5, C4, A3
- E5, D3, C1
- E1, D3, C5
- E1, C2, A3
Existem também quatro linhas de cavaleiros que atravessam o centro:
- Lá2, Dó3, Mi4
- Lá4, Dó3, Mi2
- B5, C3, D1
- Ré5, Dó3, Si1
Somando as 12 linhas de cavaleiros, chegamos a 140 + 12 = 152.
Se existem 2.300 combinações no total e 152 formam linhas, então 2.300 - 152 = 2.148 não formam linhas e, portanto, formam triângulos.
Assim, nossa resposta é 2.148/2.300 = 93,39%.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Você recebe:
- Há um avião a oito milhas diretamente acima de um míssil terra-ar, que é disparado naquele instante.
- Em todos os momentos, o avião viaja em linha reta.
- O avião viaja a 600 milhas por hora.
- O míssil viaja a uma velocidade de 2000 milhas por hora.
- O míssil sempre viaja em um ângulo que o coloca diretamente em frente ao avião.
Questões:
- Qual será a distância percorrida pelo avião antes de ser atingido pelo míssil?
- Quanto tempo levará para o míssil atingir o avião?
- Qual é o comprimento da trajetória de voo do míssil?
- Qual será a distância percorrida pelo avião antes de ser atingido pelo míssil? = 240/91 milhas
- Quanto tempo levará para o míssil atingir o avião? = 2/455 horas
- Qual será a distância percorrida pelo míssil? = 800/91 milhas
Aqui está minha solução (PDF).
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Assumir:
- 90% da população usa máscara.
- A probabilidade de contrair o coronavírus é de 1% para quem usa máscara e de 3% para quem não usa.
Uma pessoa é escolhida aleatoriamente por estar infectada com o coronavírus. Qual é a probabilidade de ela estar usando máscara?
Esta é uma questão clássica de probabilidade condicional Bayesiana.
A resposta é probabilidade(alguém usa máscara e tem coronavírus)/probabilidade(alguém tem coronavírus) =
(0,9*0,01) / (0,9*0,01 + 0,1*0,03) = 75%.
Há uma formiga no centro de um quadrado. Ela está a 17 polegadas do canto superior esquerdo, a 20 polegadas do canto superior direito e a 13 polegadas do canto inferior direito.
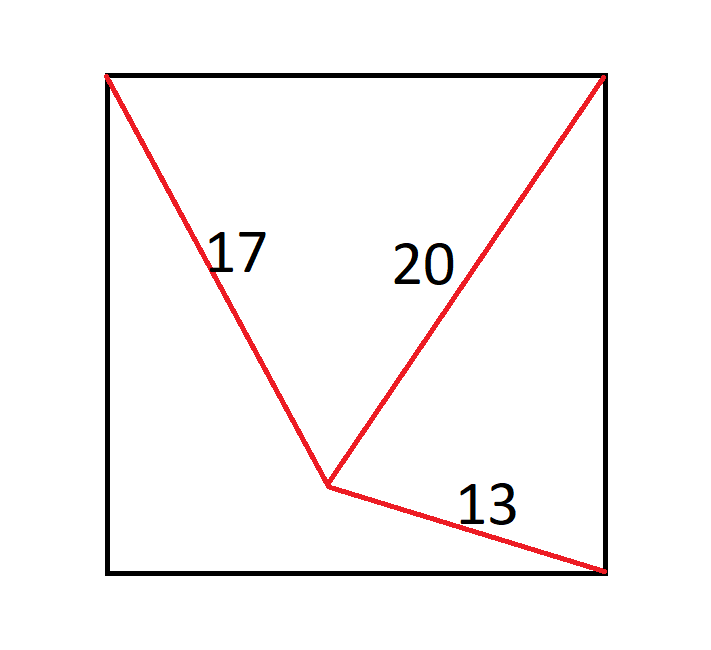
Qual o tamanho do quadrado?
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)
Primeiro, gire o triângulo ABE 90 graus para formar um novo triângulo BDF.
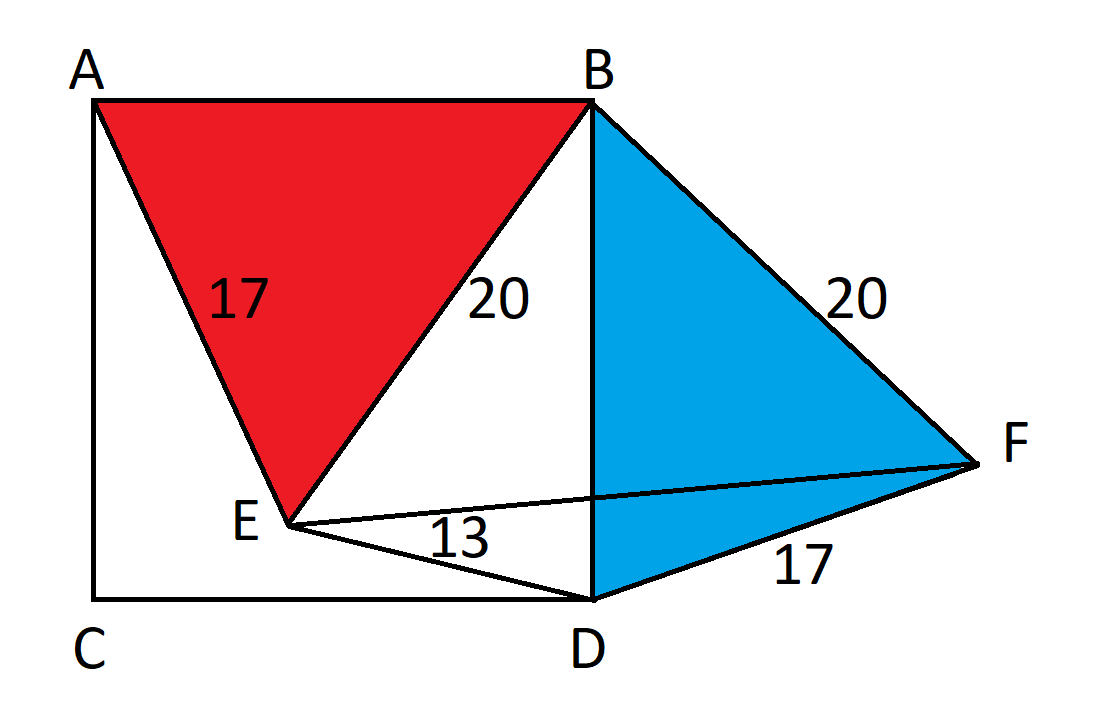
Como o triângulo foi rotacionado 90 graus, o ângulo EBF = 90, por definição. Pela fórmula de Pitágoras, EF = 20*sqrt(2).
Pela lei dos cossenos: 17^2 = 13^2 + (20*sqrt(2))^2 - 2*13*20*sqrt(2)*cos(DEF).
289 = 169 + 800 - 520*sqrt(2)*cos(DEF)
520*sqrt(2)*cos(DEF) = 680.
cos(DEF) = 17*sqrt(2)/26.
Lembre-se, sin^2(x) + cos^2(x) = 1. Vamos usar isso para resolver para sin(DEF).
sen²(DEF) + cos²(DEF) = 1
sen²(DEF) + (17√2/26)² = 1
sen²(DEF) + 289/338 = 1
sen²(DEF) = 49/338
sen(DEF) = 7*sqrt(2)/26
Em seguida, considere o ângulo BED.
Ângulo BED = Ângulo BEF + Ângulo FED.
Sabemos que o ângulo EBF mede 90 graus e que o triângulo é isósceles. Isso faria com que o ângulo BEF medisse 45 graus.
Portanto, o ângulo da cama (BED) é igual a 45 graus mais o ângulo de alimentação (FED).
Lembre-se, cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b).
cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - sin(BEF)*sin(FED)
= (1/m²(2))*17*m²(2)/26 - (1/m²(2))*7*m²(2)/26
= (17/26) - (7/26) = 10/26 = 5/13
Vamos aplicar novamente a lei dos cossenos, desta vez ao triângulo BED.
BD^2 = 20^2 + 13^2 - 2*20*13*(5/13)
= 400 + 169 - 200 = 369
BD é o lado do quadrado em questão, portanto BD^2 é a área desse quadrado, que mostramos ser 369.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Você é um pirotécnico responsável pelo espetáculo de fogos de artifício noturno em um parque de diversões. Você recebeu alguns foguetes de um modelo novo da Europa e está testando um deles para sincronizá-lo com a trilha sonora do show.
O foguete de artifício é lançado verticalmente para cima com uma aceleração constante de 4 m/s² até que o combustível químico se esgote. Sua ascensão é então desacelerada pela gravidade até atingir uma altura máxima de 138 metros, onde detona.
Considerando que não há resistência do ar e que a aceleração da gravidade é de 9,8 metros por segundo ao quadrado, quanto tempo leva para o foguete atingir sua altura máxima?
Deixar:
t = tempo decorrido desde que o combustível do foguete acabou.
r = tempo de duração do combustível do foguete.
Vou expressar a aceleração em termos de uma direção ascendente. Portanto, a aceleração após o combustível do foguete se esgotar é -9,8.
Só para relembrar, a integral da aceleração é a velocidade e a integral da velocidade é a posição. Vamos considerar a posição em relação ao solo.
Quando o foguete é lançado pela primeira vez, é-nos dado que a aceleração é 4.
Calculando a integral, a velocidade do foguete após r segundos é igual a 4r.
A integral da velocidade nos dá a localização do foguete após r segundos de 2r 2 .
Agora vejamos o que acontece depois que o combustível do foguete se esgota.
Sabemos que a aceleração da gravidade é -9,8.
A velocidade devido à gravidade no instante t é -9,8t. No entanto, ela também possui uma velocidade ascendente de 4r devido ao foguete.
Seja v(t) = velocidade no instante t
v(t) = -9,8t + 4r
O foguete atingirá a altura máxima quando v(t) = 0. Vamos calcular isso.
v(t) = 0 = -9,8t + 4r
4r = 9,8t
t = 40/98 r = 20r/49.
Em outras palavras, seja qual for o tempo que o combustível do foguete durar, ele continuará subindo por 20/49 desse tempo.
Também nos foi informado que a distância percorrida na altitude máxima atingida é de 138 metros.
Vamos calcular a integral de v(t) para obter a fórmula da distância percorrida, que chamaremos de d(t).
d(t) = -4,9t 2 + 4rt + c, onde c é uma constante de integração.
Como já mostramos, o foguete percorreu 2r² até o combustível se esgotar, então essa deve ser a constante de integração. Isso nos dá:
d(t) = -4,9t² + 4rt + 2r²
Sabemos que a altitude máxima de 138 foi atingida no instante 20r/49. Então, vamos substituir t = 20r/49 na equação para encontrar o valor de r:
d((20r/49) = -4,9((20r/49) 2 + 4r(20r/49) + 2r 2 = 138
r 2 *(-1960/2401 + 80/49 + 2) = 138
r 2 = 49
r = 7
Assim, o combustível do foguete durou sete segundos.
Já sabemos que o foguete continuou subindo por 20/49 desse tempo, o que é 140/49 = aproximadamente 2,8571 segundos.
Assim, o tempo desde o lançamento até a velocidade máxima é de 7 + 140/49 = 483/49 = aproximadamente 9,8571 segundos.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Qual é o número esperado de lançamentos de dois dados para se obter qualquer total de 2 a 12? Por favor, utilize cálculo para sua resposta.
Lembre-se que a probabilidade de rolar um total de 2 é 1/36. Em t lançamentos, o número esperado de lançamentos com um total de 2 é t/36. Suponha que o tempo entre os lançamentos seja distribuído exponencialmente com uma média de t/36. A distribuição de Poisson nos diz que a probabilidade de zero lançamentos com um total de 2 é exp(-t/36).
Lembre-se que a probabilidade de rolar um total de 3 é 2/36 = 1/18. Pela mesma lógica, a distribuição de Poisson nos diz que a probabilidade de rolar zero com um total de 3 é exp(-t/18).
Lembre-se que a probabilidade de rolar um total de 4 é 3/36 = 1/12. Pela mesma lógica, a distribuição de Poisson nos diz que a probabilidade de rolar zero com um total de 4 é exp(-t/12).
Lembre-se que a probabilidade de rolar um total de 5 é 4/36 = 1/9. Pela mesma lógica, a distribuição de Poisson nos diz que a probabilidade de rolar zero com um total de 5 é exp(-t/9).
Lembre-se que a probabilidade de rolar um total de 6 é 5/36. Pela mesma lógica, a distribuição de Poisson nos diz que a probabilidade de rolar zero com um total de 6 é exp(-5t/36).
Lembre-se que a probabilidade de rolar um total de 7 é 6/36 = 1/6. Pela mesma lógica, a distribuição de Poisson nos diz que a probabilidade de rolar zero com um total de 7 é exp(-t/6).
As probabilidades de 8 a 12 são as mesmas que as de 2 a 6.
Assim, a probabilidade de que em t unidades de cada total tenha sido rolado pelo menos uma vez é:
(1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
A probabilidade de que pelo menos o total NÃO tenha sido rolado em t unidades de tempo é 1 - (1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
Para obter o tempo esperado sem pelo menos um total, integramos a função acima de 0 ao infinito.
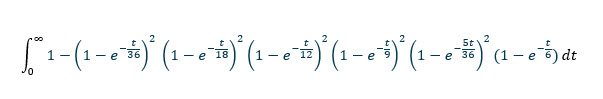
Uma calculadora de integrais (recomendo esta ) resolverá facilmente isso como 769767316159/12574325400 = aproximadamente 61,2173847639572 rolos.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Um paralelepípedo é um bloco tridimensional composto por quadrados unitários.
Um paralelepípedo de dimensões a × b × c é construído a partir de abc cubos unitários idênticos, como um cubo de Rubik 3x3x3. Divida os cubos em dois tipos mutuamente exclusivos. Os cubos externos são aqueles que constituem as faces do paralelepípedo; os cubos internos são aqueles que o envolvem completamente. Por exemplo, o paralelepípedo ilustrado possui 74 cubos externos e 10 cubos internos.
Determine as dimensões de todos os paralelepípedos de forma que o número de cubos externos seja igual ao número de cubos internos.
- 5 x 13 x 132
- 5 x 14 x 72
- 5 x 15 x 52
- 5 x 16 x 42
- 5 x 17 x 36
- 5 x 18 x 32
- 5 x 20 x 27
- 5 x 22 x 24
- 6 x 9 x 56
- 6 x 10 x 32
- 6 x 11 x 24
- 6 x 12 x 20
- 6 x 14 x 16
- 7 x 7 x 100
- 7 x 8 x 30
- 7 x 9 x 20
- 7 x 10 x 16
- 8 x 8 x 18
- 8 x 9 x 14
- 8 x 10 x 12
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Seja 0 < a < b. Qual é maior que a^b ou b^a?
A resposta depende especificamente de a e b, mas duas regras práticas abrangem a maioria das situações.
Se a > e, então a^b > b^a
Se b < e, então a^b < b^a
Se a < e e b > e, então não há informações suficientes para determinar.
Aqui está a solução (PDF).
Uma granada é lançada em um poço sem fundo. Em média, a granada explode em seis segundos. O tempo até a explosão possui uma propriedade de ausência de memória, ou seja, a probabilidade de uma explosão em qualquer instante é sempre a mesma e independente de quanto tempo se passou desde que o pino foi acionado. Em outras palavras, sua vida útil segue uma distribuição exponencial. Considere uma aceleração de 32 pés por segundo ao quadrado.
Segue minha solução completa (PDF).
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Imagine um programa de jogos com dois participantes que são ambos egoístas e lógicos natos. Eis as regras.
- O apresentador coloca US$ 1.000.000 em uma mesa entre os dois participantes.
- Ao participante A é solicitado que faça uma sugestão sobre como dividir o dinheiro entre os dois participantes.
- O participante B será solicitado a aceitar ou rejeitar a sugestão.
- Se o participante B aceitar a sugestão, o dinheiro será dividido dessa forma e o jogo terminará.
- Caso o participante B rejeite a sugestão, o apresentador removerá 10% do valor atualmente em jogo.
- O apresentador pedirá então ao participante B que faça uma sugestão e o participante A terá a mesma oportunidade de aceitá-la ou rejeitá-la.
- Se o participante A aceitar a sugestão, o valor é dividido dessa forma e o jogo termina. Se ele rejeitar, o apresentador recolhe mais 10% do valor restante na mesa. Em seguida, volte ao passo 2 e repita o processo até que uma sugestão seja aceita.
A questão é: como o participante A deve sugerir a divisão do dinheiro em sua primeira jogada?
Ele deveria sugerir ficar com 10/19 do dinheiro para si, menos um centavo, e oferecer a B 9/19 do dinheiro, mais um centavo. Em outras palavras:
A: $ 526.315,78
B: $ 473.684,22
A chave é que A coloque B o mais próximo possível de um ponto de indiferença.
Vamos chamar a proporção entre o pote e o outro jogador de r. Se B aceitar a oferta, ele receberá r × US$ 1.000.000.
Se B rejeitar a oferta, o apresentador fica com 10%. Depois disso, B terá uma vantagem posicional e poderá oferecer ao participante A uma parte de r e ficar com 1-r para si.
Resolvendo para r...
r×$1.000.000 = (1-r)×$900.000.
r × US$ 1.900.000 = US$ 900.000.
r = $900.000/$1.900.000 = 9/19.
A não quer que B seja completamente indiferente, para que A não escolha aleatoriamente e corra o risco de o anfitrião levar todo o prêmio. Portanto, A deve oferecer a B um centavo extra e lhe dar (9/19) × $1.000.000 + $0,01 = $473.684,22.
A: $ 526.315,78
B: $ 473.684,22
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Duas cidades, Fauntleroy e Southworth, ficam separadas por um canal. Duas balsas fazem a travessia entre as duas cidades o dia todo. As balsas viajam em velocidades diferentes. Ao mesmo tempo, ambas partem, uma de cada cidade.
A primeira travessia ocorre a 8 km de Southworth. A segunda travessia ocorre a 5 km de Fauntleroy. Considere que não há tempo para carga e descarga, mas que ambos os veículos fazem um retorno imediato. Considere também que seguem em linha reta.
Qual a distância entre as duas cidades?
Seja t₂ o tempo até o segundo cruzamento.
r = razão entre a velocidade inicial da balsa ao sair de Fauntleroy e a velocidade inicial da balsa ao sair de Southworth.
c = Distância do canal entre duas cidades.
Sabemos que a primeira vez que eles se cruzam é a 5 milhas de Southworth. Para expressar isso em fórmulas:
c-5 = r*t 1
5 = t 1
Igualando t 1 , obtemos:
c-5 = 5r, ou r = (c-5)/5
Também nos foi informado que a segunda vez que eles cruzam o rio é a 3 milhas de Fauntleroy. Para expressar isso em fórmulas:
3c - 3 = r*t 2
c+3 = t 2
Igualando t 2 , obtemos:
2c - 3 = r*(c+3)
Substitua r=(c-5)/5
2c-3 = [(c-5)/5] * (c+3)
10c - 15 = c² - 2c - 15
c² - 12c = 0 c - 12 = 0 c = 12
Portanto, o canal tem 12 milhas de comprimento.
No diagrama a seguir, qual é a área da região azul?
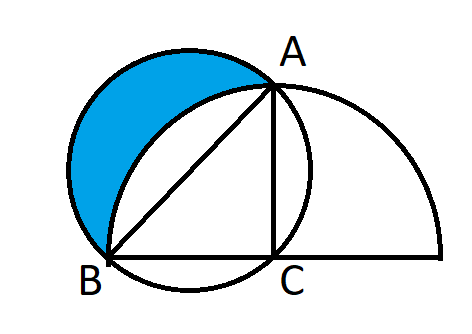
Clique no botão abaixo para ver a resposta.
Aqui está minha solução (PDF).
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Em um torneio de xadrez, cada participante joga uma partida contra todos os outros. Cada participante recebe 1 ponto por cada partida que vence, 0,5 pontos por cada partida empatada e 0 pontos por cada partida que perde.
Ao final do torneio, constatou-se que todos os competidores obtiveram números diferentes de pontos e o último colocado na classificação derrotou cada um dos três primeiros colocados.
Assim sendo, qual é o número mínimo de competidores que participam do torneio?
Vamos chamar o número de jogadores de n.
Considero que o jogador em último lugar tem apenas três vitórias, contra os 3 melhores jogadores, e perdeu todas as outras partidas. Isso lhe dá 3 pontos.
Em seguida, considero que cada jogador subsequente, em ordem de pontos, tem 0,5 pontos a mais que o anterior, na classificação. Isso daria ao jogador de classificação mais alta 3+(n-1)/2 pontos.
Fazendo a soma de 3 com 3+(n-1)/2, por 1/2 ponto por passo, obtemos (((n+5)*(n+6)/2)-15)/2.
O número total de partidas jogadas com n jogadores é n*(n-1)/2, onde cada jogador joga contra todos os outros uma vez. Cada partida resulta em um ponto, que também é o total de pontos ganhos por todos os jogadores.
Em seguida, resolva para n:
(((n+5)*(n+6)/2)-15)/2 = n*(n-1)/2
((n+5)*(n+6)/2)-15 = n*(n-1)
(n+5)*(n+6)/2 = n*(n-1) + 15
(n+5)*(n+6) = 2*n*(n-1) + 30
n^2 + 11n + 30 = 2n^2 - 2n + 30
n² + 11n = 2n² - 2n
n + 11 = 2n-2
n=13
A tabela a seguir mostra uma maneira pela qual isso pode acontecer. O corpo da tabela mostra o vencedor em todos os 78 jogos.
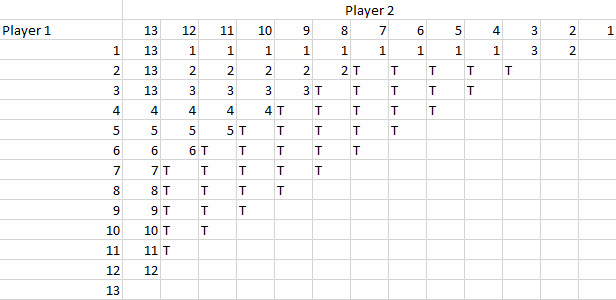
A tabela a seguir mostra o número de pontos de cada jogador.
Total de pontos por jogador
| Jogador | Pontos |
|---|---|
| 13 | 3 |
| 12 | 3,5 |
| 11 | 4 |
| 10 | 4.5 |
| 9 | 5 |
| 8 | 5.5 |
| 7 | 6 |
| 6 | 6,5 |
| 5 | 7 |
| 4 | 7,5 |
| 3 | 8 |
| 2 | 8,5 |
| 1 | 9 |
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Qual é a maneira mais eficiente de empilhar balas de canhão: em uma pirâmide de base quadrada, como as pirâmides do Egito, ou em uma pirâmide triangular, formando um tetraedro?


Aqui estão algumas fórmulas que o leitor pode achar úteis:
Deslize para baixo para ver minha resposta e solução.
Por "eficiente", presumo que você queira dizer qual arma tem o menor espaço desperdiçado entre as balas de canhão.
Para simplificar, e para definir o volume de cada pirâmide, vamos usar o centro das bolas localizadas nos vértices da pirâmide. Vamos considerar n como o número de balas de canhão em cada lado da base de cada pirâmide.
Vamos analisar primeiro a pirâmide com base quadrada.
O número de balas de canhão em toda a pirâmide é 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 + ... + n 2 = n*(n+1)*(2n+1)/6.
Em seguida, vamos encontrar a altura desta pirâmide quadrada onde um lado da base mede n. Como pode ser visto na figura, os lados (exceto a base quadrada) são triângulos equiláteros. Portanto, a geratriz também mede n. A distância de um canto da base ao canto oposto é n√2. A distância de um canto da base ao centro da base é, portanto, n√2/2. Seja h a altura. Considere o triângulo retângulo formado pela altura, a distância de um canto da base ao centro da base e a geratriz.
h 2 + (n*sqrt(2)/2) 2 = n 2
h = n*sqrt(2)/2.
Lembre-se que o volume de uma pirâmide é dado por base * altura / 3. Isso torna o volume da pirâmide:
n 2 * n* quadrado(2)/2 * (1/3) = n 3 *sqrt(2)/6.A razão entre bolas e volume é, portanto, [n*(n+1)*(2n+1)/6] / [n 3 *sqrt(2)/6] = sqrt(2)*n*(n+1)*(2n+1)/(2*n 3 ) = sqrt(2)*(n+1)*(2n+1)/(2*n 2 )
Em seguida, vamos analisar a pirâmide com base triangular.
O número de balas de canhão em toda a pirâmide é 1 + 3 + 6 + 10 + 15 + ... + n*(n+1)/2 = n*(n+1)*(n+2)/6.
Em seguida, vamos encontrar a área da base. Lembre-se, os lados de um triângulo 30-60-90 são proporcionais a 1/2, √3/2 e 1. A partir disso, não é difícil encontrar a altura de um triângulo equilátero de lado n, que é n√3/2. Isso faz com que a área da base seja n²√3 /4.
A distância de um canto da base ao centro da base é sqrt(3)/3. Dado isso e a altura inclinada de 1 da pirâmide, podemos usar o teorema de Pitágoras para encontrar a altura da pirâmide como sqrt(6)/3.
Agora podemos encontrar o volume da pirâmide como base*altura/3 = (n 2 *sqrt(3)/4) * (n*sqrt(6)/3) * (1/3) = n 3 *sqrt(18)/36 = n 3 *sqrt(2)/12.
A razão entre o número de bolas e o volume é, portanto, [n*(n+1)*(n+2)/6] / [ n³ *√2/12] = √2*n*(n+1)*(2n+1)/(2* n³ ) = √2*(n+1)*(n+2)/ n²
Segue uma comparação das proporções entre o volume das bolas e o volume total:
- Base quadrada: sqrt(2)*(n+1)*(2n+1)/(2*n 2 )
- Base do triângulo: sqrt(2)*(n+1)*(n+2)/n 2
Vamos dividir ambas as razões por sqrt(2)*(n+1)/n 2 :
- Base quadrada: (2n+1)/2 = n + 0,5
- Base do triângulo: n+2
À medida que n aumenta, a proporção entre o número de balas e o volume se aproximará de n para ambas as pirâmides. Em outras palavras, quanto maior o número de balas de canhão, mais igualmente eficientes elas serão.
Dado o volume de uma bala de canhão, a eficiência em ambas as pirâmides, definida como a razão entre o volume da bala de canhão e o volume total, aproxima-se de pi*sqrt(2)/6 ≈ 74,05%.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Para um dado número grande, qual é a distância média entre os números primos próximos a esse número? Além disso, quantos números primos são menores que esse número?
Uma estimativa muito boa para a distância média entre primos próximos de qualquer número grande n é ln(n). É notável o quão bom é esse estimador.
Como evidência, a tabela a seguir mostra a amplitude dos primeiros 15 milhões de números primos, em grupos de um milhão. A tabela mostra a distância média entre os números primos dentro desse intervalo, bem como a estimativa dessa distância média. A estimativa é o logaritmo natural da média entre o maior e o menor número primo no intervalo. Por exemplo, para o 15º grupo de um milhão de números primos, a estimativa é ln((256.203.221 + 275.604.541)/2).
Distância média entre números primos
| Primeiro Prime em alcance | Último Prime em alcance | Números primos em alcance | Distância média | Estimativa | |
|---|---|---|---|---|---|
| 2 | 15.485.863 | 1.000.000 | 15,485861 | 15,86229105 | |
| 15.485.867 | 32.452.843 | 1.000.000 | 16,966976 | 16,9922867 | |
| 32.452.867 | 49.979.687 | 1.000.000 | 17,52682 | 17,53434381 | |
| 49.979.693 | 67.867.967 | 1.000.000 | 17,888274 | 17,89175615 | |
| 67.867.979 | 86.028.121 | 1.000.000 | 18.160142 | 18.15864108 | |
| 86.028.157 | 104.395.301 | 1.000.000 | 18.367144 | 18,3716137 | |
| 104.395.303 | 122.949.823 | 1.000.000 | 18,55452 | 18,54883262 | |
| 122.949.829 | 141.650.939 | 1.000.000 | 18.70111 | 18.70058553 | |
| 141.650.963 | 160.481.183 | 1.000.000 | 18.83022 | 18,83322787 | |
| 160.481.219 | 179.424.673 | 1.000.000 | 18,943454 | 18.95103217 | |
| 179.424.691 | 198.491.317 | 1.000.000 | 19.066626 | 19.05703535 | |
| 198.491.329 | 217.645.177 | 1.000.000 | 19,153848 | 19,15337672 | |
| 217.645.199 | 236.887.691 | 1.000.000 | 19.242492 | 19,24163365 | |
| 236.887.699 | 256.203.161 | 1.000.000 | 19.315462 | 19.32305683 | |
| 256.203.221 | 275.604.541 | 1.000.000 | 19.40132 | 19,39864545 |
Fonte: As lacunas entre os preços Prime no Prime Pages.
Para obter o número de números primos menores que qualquer número dado, podemos começar integrando a estimativa da distância média de ln(n). Isso nos dará a soma das distâncias médias entre números primos até qualquer número n.
Qual é a integral de f(n)=ln(n)? Lembre-se que a integração por partes nos diz:
Integral de f(n)*g'(n) dn = f(n)*g(n) - integral de (f'(n)*g(n)) dn
Sejam f(n)=ln(n) e g'(n)=1. Então f'(n)=1/n e g(n)=n. A integral de ln(n) será, portanto, ln(n)*n - integral de ((1/n)*n) = ln(n)*n - n = n*(ln(n)-1)
Se dividirmos n*(ln(n)-1) por n, obtemos a distância média entre primos no intervalo de números de 2 a n. Isso é ln(n)-1.
Se dividirmos n por essa distância média entre primos, obtemos o número médio de primos menores que n, que é igual a n/(ln(n)-1).
Como prova, a tabela a seguir mostra o número de números primos sob vários números grandes e o valor estimado. Peço desculpas pela precisão de 15 dígitos significativos, que é o máximo que o Excel permite. Alguém, por favor, crie uma planilha que suporte mais.
Distância média entre números primos
| n | Números primos menores que n | n/(ln(n)-1) |
|---|---|---|
| 10 | 4 | 8 |
| 100 | 25 | 28 |
| 1.000 | 168 | 169 |
| 10.000 | 1.229 | 1.218 |
| 100.000 | 9.592 | 9.512 |
| 1.000.000 | 78.498 | 78.030 |
| 10.000.000 | 664.579 | 661.459 |
| 100.000.000 | 5.761.455 | 5.740.304 |
| 1.000.000.000 | 50.847.534 | 50.701.542 |
| 10.000.000.000 | 455.052.511 | 454.011.971 |
| 100.000.000.000 | 4.118.054.813 | 4.110.416.301 |
| 1.000.000.000.000 | 37.607.912.018 | 37.550.193.650 |
| 10.000.000.000.000 | 346.065.536.839 | 345.618.860.221 |
| 100.000.000.000.000 | 3.204.941.750.802 | 3.201.414.635.781 |
| 1.000.000.000.000.000 | 29.844.570.422.669 | 29.816.233.849.001 |
| 10.000.000.000.000.000 | 279.238.341.033.925 | 279.007.258.230.820 |
| 100.000.000.000.000.000 | 2.623.557.157.654.230 | 2.621.647.966.812.030 |
| 1.000.000.000.000.000.000 | 24.739.954.287.740.800 | 24.723.998.785.920.000 |
| 10.000.000.000.000.000.000 | 234.057.667.276.344.000 | 233.922.961.602.470.000 |
| 100.000.000.000.000.000.000 | 2.220.819.602.560.910.000 | 2.219.671.974.013.730.000 |
| 1.000.000.000.000.000.000.000 | 21.127.269.486.018.700.000 | 21.117.412.262.910.000.000 |
| 10.000.000.000.000.000.000.000 | 201.467.286.689.315.000.000 | 201.381.995.844.660.000.000 |
| 100.000.000.000.000.000.000.000 | 1.925.320.391.606.800.000.000 | 1.924.577.459.166.810.000.000 |
| 1.000.000.000.000.000.000.000.000 | 18.435.599.767.349.200.000.000 | 18.429.088.896.563.900.000.000 |
| 10.000.000.000.000.000.000.000.000 | 176.846.309.399.143.000.000.000 | 176.788.931.049.964.000.000.000 |
Fonte: Quantos números primos existem? em Prime Pages.
A figura acima é um eneágono com lado de comprimento um.
Qual é maior, AB+AC ou AE?
Este problema foi retirado da edição de março de 2021 do Boletim da Mensa.
Aqui está a minha solução para este problema. (PDF)
Como posso encontrar facilmente a raiz quadrada de qualquer número de três ou quatro dígitos, assumindo que a resposta seja um número inteiro?
A tabela a seguir mostra os números de 0 a 9, o quadrado de cada um deles e o último dígito desse quadrado.
Último dígito de números quadrados
| Original Número | Quadrado | Último dígito da Praça |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 4 |
| 3 | 9 | 9 |
| 4 | 16 | 6 |
| 5 | 25 | 5 |
| 6 | 36 | 6 |
| 7 | 49 | 9 |
| 8 | 64 | 4 |
| 9 | 81 | 1 |
Note que os quadrados dos números pares sempre terminam em 0, 1, 4, 5, 6 ou 9. Isso é válido para todos os quadrados. Isso ocorre porque o último dígito do número original determina o último dígito do quadrado.
Passo 1: Com base no último dígito do quadrado, podemos usar a seguinte tabela para identificar o último dígito da raiz quadrada. Por exemplo, se 2809 for o quadrado, o último dígito da raiz quadrada será 3 ou 7.
Último dígito do número original
| Último dígito da raiz quadrada | Último dígito da Praça |
|---|---|
| 0 | 0 |
| 1 | 1 ou 9 |
| 4 | 2 ou 8 |
| 5 | 5 |
| 6 | 4 ou 6 |
| 9 | 3 ou 7 |
Passo 2: Em seguida, pegue o número original e descarte os dois dígitos da direita. Por exemplo, se o número original fosse 2809, use 28.
Passo 3: Encontre o menor número quadrado menor ou igual ao resultado do passo 2. Em seguida, calcule a raiz quadrada desse número quadrado. Por exemplo, o menor quadrado menor que 28 é 25. Calculando a raiz quadrada de 25, obtemos 5.
Se você não memorizou os quadrados até 100, pode usar a tabela a seguir.
Primeira parte da raiz quadrada
| Passo 2 | Passo 3 |
|---|---|
| 1 a 3 | 1 |
| 4 a 8 | 2 |
| 9 a 15 | 3 |
| 16 a 24 | 4 |
| 25 a 35 | 5 |
| 36 a 48 | 6 |
| 49 a 63 | 7 |
| 64 a 80 | 8 |
| 81 a 99 | 9 |
Passo 4: Se o resultado do passo 1 for 0 ou 5, coloque-o após o resultado do passo 3 e você terminou.
Caso contrário, seja a = resultado da etapa 3. Seja b = a × (a + 1). Por exemplo, se o resultado da etapa 3 for 5, então b = 5 × 6 = 30.
Passo 5: Se b < a, então o último dígito da raiz quadrada é o menor dos valores possíveis obtidos no passo 1. Caso contrário, se b >= a, então é o maior dos dois valores possíveis.
Passo 6: Para obter a raiz quadrada, pegue o resultado do passo 3 e some-o ao resultado do passo 5. Em outras palavras, 10 × (passo 3) + passo 5.
Vejamos alguns exemplos:
Calcule a raiz quadrada de 256.
- Passo 1: O último dígito da raiz quadrada é 4 ou 6.
- Passo 2: Eliminando os dois últimos dígitos, obtemos 2.
- Passo 3: O menor quadrado menor ou igual a 2 é 1. A raiz quadrada de 1 é 1.
- Passo 4: 1*(1+1) = 2.
- Passo 5: O resultado do passo 4 é igual ao do passo 2, então usamos a maior das opções do passo 1 como o último dígito, que é 6.
- Passo 6: A raiz quadrada é o resultado de 3 somado ao resultado do passo 5, que resulta em 1 e 6 = 16.
Calcule a raiz quadrada de 1369.
- Passo 1: O último dígito da raiz quadrada é 3 ou 7.
- Passo 2: Eliminando os dois últimos dígitos, obtemos 13.
- Passo 3: O menor quadrado menor ou igual a 13 é 9. A raiz quadrada de 9 é 3.
- Passo 4: 3*(1+3) = 12.
- Passo 5: O resultado do passo 2 é maior que o do passo 4, então usamos a maior das opções do passo 1 como o último dígito, que é 7.
- Passo 6: A raiz quadrada é o resultado de 3 somado ao resultado do passo 5, que resulta em 3 e 7 = 37.
Calcule a raiz quadrada de 2704.
- Passo 1: O último dígito da raiz quadrada é 2 ou 8.
- Passo 2: Eliminando os dois últimos dígitos, obtemos 27.
- Passo 3: O menor quadrado menor ou igual a 27 é 25. A raiz quadrada de 25 é 5.
- Passo 4: 5*(1+5) = 60.
- Passo 5: O resultado do passo 2 é menor que o do passo 4, então usamos o menor dos valores do passo 1 como o último dígito, que é 2.
- Passo 6: A raiz quadrada é o resultado de 3 somado ao resultado do passo 5, que resulta em 5 e 2 = 52.
Calcule a raiz quadrada de 5625.
- Passo 1: O último dígito da raiz quadrada é 5.
- Passo 2: Eliminando os dois últimos dígitos, obtemos 56.
- Passo 3: O menor quadrado menor ou igual a 56 é 49. A raiz quadrada de 49 é 7.
- Passo 4: O resultado do passo 1 é 0 ou 5, então a resposta é o resultado do passo 3 somado ao do passo 1: 7 e 5 = 75
Calcule a raiz quadrada de 6561.
- Passo 1: O último dígito é 1 ou 9.
- Passo 2: Eliminando os dois últimos dígitos, obtemos 65.
- Passo 3: O menor quadrado menor ou igual a 65 é 64. A raiz quadrada de 64 é 8.
- Passo 4: 8*(1+8) = 72.
- Passo 5: O resultado do passo 2 é menor que o do passo 4, então usamos o menor dos valores do passo 1 como o último dígito, que é 1.
- Passo 6: A raiz quadrada é o resultado de 3 somado ao resultado do passo 5, que dá 8 e 1 = 81.
Você pode ver uma demonstração desse método no YouTube .
Qual é a área de um pentágono regular com lado de comprimento 1?
Clique na caixa abaixo para ver a resposta.
Clique na caixa abaixo para obter uma dica.
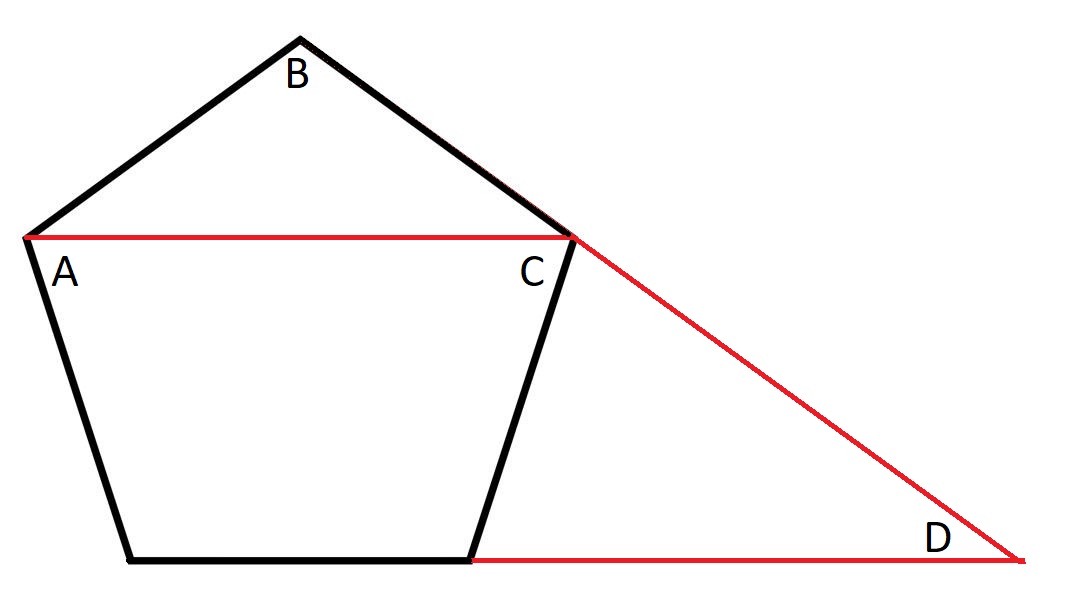
Considere a imagem acima. AC = CD.
Aqui está minha solução (PDF)
Num dia sem vento, Charlie leva sua canoa para o rio e rema rio acima. Ele sempre rema no mesmo ritmo (em outras palavras, se ignorarmos a correnteza, ele sempre remaria na mesma velocidade). Uma milha depois de entrar na água, seu chapéu cai no rio. Dez minutos depois, ele percebe que seu chapéu sumiu e imediatamente dá meia-volta para recuperá-lo rio abaixo. Charlie alcança seu chapéu no mesmo lugar onde começou a remar.
Qual a velocidade da corrente elétrica?
Clique no botão abaixo para ver a resposta.
Aqui está minha solução (PDF).
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
A seguinte questão refere-se a uma aposta de bar. Um número de série aleatório de uma nota de dinheiro americana é usado. O jogador seleciona três dígitos quaisquer de 0 a 9. Ele deve selecionar três números diferentes. Os ganhos são baseados em quantos desses três dígitos selecionados aparecem pelo menos uma vez no número de série.
Por exemplo, se a seleção de jogadores for 7-0-2 e o número de série for 22227755, então há duas correspondências. Não importa que o 2 e o 7 tenham ocorrido várias vezes.
Eis as probabilidades oferecidas:
- 3 partidas: 5 a 1
- 2 partidas: 1 a 1
- 1 partida: 9 a 5
- 0 partidas: 15 a 1
Qual é a probabilidade de ganhar e a vantagem da casa em cada aposta?
A tabela a seguir mostra o número de combinações vencedoras, a probabilidade de ganhar e a vantagem da casa para cada aposta. A coluna da direita mostra que a vantagem da casa varia de 7,4% a 8,5%.
Apostas com Número de Série
| Partidas | Paga | Combinações | Probabilidade | Borda da casa |
|---|---|---|---|---|
| 3 | 5 | 15.426.684 | 0,154267 | 0,074399 |
| 2 | 1 | 45.771.270 | 0,457713 | 0,084575 |
| 1 | 1.8 | 33.037.245 | 0,330372 | 0,074957 |
| 0 | 15 | 5.764.801 | 0,057648 | 0,077632 |
Utilizando cada dígito de 1 a 9 exatamente uma vez, componha três frações, cada uma com um dígito no numerador e dois dígitos no denominador, em que a soma das três frações seja um.
Por exemplo, 8/16 + 9/27 + 3/24 satisfaz todas as condições, exceto que a soma é igual a 23/24, e não a 1.
Existem permut(9,3)*permut(6,3)*permut(3,3)/fact(3) = 60.480 permutações possíveis para analisar e encontrar a resposta. Devo admitir que tentei por pelo menos uma hora, por tentativa e erro, e não encontrei uma solução.
Então, escrevi um programa para percorrer todas as 362.880 maneiras possíveis de ordenar os nove dígitos e testei todas elas. A parte complicada foi percorrer todas as formas possíveis de ordenar os nove números. Veja como fazer isso, usando ordenação lexicográfica.
- Coloque todos os nove elementos em uma matriz, organizados do menor para o maior.
- Encontre o último elemento da matriz que seja maior que o elemento seguinte. Se nenhum for encontrado, encerre o programa.
- Começando pelo elemento seguinte ao da etapa 2, encontre o último elemento na matriz que seja maior que o da etapa 2.
- Troque os elementos da matriz das etapas 2 e 3.
- Inverta a ordem dos elementos na matriz, começando pelo elemento seguinte ao da etapa 2 e seguindo até o final.
- Voltar para a etapa 2
Seguindo esse processo, você encontrará a resposta correta seis vezes, uma vez para cada uma das seis maneiras de ordenar as três frações.
[spoiler=Código]
Escrevi o seguinte código para ordenar cada dígito de 1 a 9 em ordem lexicográfica e testar se cada um era uma solução.
vazio três_frações(vazio)
{
int i, x_max, y_max, temp_array[100], hold, pt;
int lex_array[] = { 1,2,3,4,5,6,7,8,9 };
int num_elements = sizeof(lex_array) / sizeof(lex_array[0]);
int contagem = 0;
bool stop = falso;
total duplo 3;
cerr << "Número de elementos =\t" << num_elements << "\n";
fazer
{
contar++;
tot3 = (double)lex_array[0] / (double)(10 * lex_array[1] + lex_array[2]);
tot3 += (double)lex_array[3] / (double)(10 * lex_array[4] + lex_array[5]);
tot3 += (double)lex_array[6] / (double)(10 * lex_array[7] + lex_array[8]);
se (tot3 == 1.0)
{
cerr << count << "\t";
cerr << lex_array[0] << "/" << lex_array[1] << lex_array[2] << " + ";
cerr << lex_array[3] << "/" << lex_array[4] << lex_array[5] << " + ";
cerr << lex_array[6] << "/" << lex_array[7] << lex_array[8] << "\n";
}
x_max = -1;
para (i = 0; i < (num_elementos - 1); i++)
{
se (lex_array[i] < lex_array[i + 1])
x_max = i;
}
se (x_max >= 0)
{
y_max = 0;
para (i = x_max + 1; i < num_elementos; i++)
{
se (lex_array[x_max] < lex_array[i])
y_max = i;
}
hold = lex_array[x_max];
lex_array[x_max] = lex_array[y_max];
lex_array[y_max] = hold;
se (x_max + 1 < num_elementos - 1) // inverter
{
para (i = x_max + 1; i < num_elementos; i++)
{
temp_array[i] = lex_array[i];
}
pt = 0;
para (i = x_max + 1; i < num_elementos; i++)
{
lex_array[i] = temp_array[num_elements - 1 - pt];
pt++;
}
}
}
outro
parar = verdadeiro;
} enquanto (parar == falso);
}
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Um homem tinha um barril de vinho de 10 galões e um jarro. Certo dia, ele encheu o jarro com vinho e completou o barril com água. Mais tarde, quando o vinho e a água já estavam bem misturados, ele encheu outro jarro com vinho e completou o barril novamente com água. O barril ficou então com quantidades iguais de vinho e água.
Qual era a capacidade da jarra?
Seja j = volume da jarra.
Após o primeiro enchimento do jarro, restaram 10-j galões de vinho no jarro. Depois que a água substituiu o vinho, a proporção de vinho para todo o barril foi (10-j)/10.
Após a jarra retirar o vinho diluído, restaram 10 galões de vinho diluído no barril. A quantidade de vinho puro no vinho diluído pode ser expressa como:
(10-j)*((10-j)/10) = 5
(10-j)^2 = 50
j² - 20j + 100 = 50
j² - 20j + 50 = 0
j = (20 +/- sqrt(400-200))/2
j = (20 +/- 10*sqrt(2))/2
j = 10 +/- 5*sqrt(2)
O jarro não pode ser maior que o barril, portanto devemos usar o sinal negativo:
j = 10 - 5*sqrt(2) =~ aproximadamente 2,92893218813452 galões.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Para celebrar o Dia de Ação de Graças, você e 19 matemáticos estão sentados em uma mesa redonda. Todos na mesa gostariam de uma porção de molho de cranberry, que por acaso está à sua frente neste momento.
Primeiro, você se serve. Depois, em vez de passar o molho em círculo, você decide passá-lo aleatoriamente para a pessoa sentada diretamente à sua esquerda ou à sua direita. Essa pessoa, por sua vez, faz o mesmo, passando o molho aleatoriamente para a pessoa à sua esquerda ou à sua direita. Isso continua até que todos tenham, em algum momento, recebido o molho de cranberry.
Das 20 pessoas no círculo, quem tem a maior probabilidade de ser o último a receber o molho de cranberry?
Vamos escolher um matemático como G. Para que G seja o último, duas coisas devem acontecer:
- Os arandos devem primeiro chegar a um dos vizinhos de G.
- Os cranberries devem se mover 19 posições na direção oposta sem nunca chegar a G.
Para serem as últimas, as cranberries precisam eventualmente alcançar um dos vizinhos. Portanto, a probabilidade disso acontecer é de 100%.
Então, qualquer que seja a probabilidade da segunda parte, ela é a mesma para cada pessoa. Portanto, cada pessoa tem a mesma probabilidade de ser a última.
Caso essa explicação não tenha sido clara, Gialmere obteve esse problema do fivethirtyeight.com. Lá eles explicam a solução . Role a página para baixo até a parte que diz "Solução para o Charada Clássico da semana passada".
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Aqui está mais um enigma do Charada .
Há 100 bolinhas de gude em um saco. Cada bolinha é vermelha, azul ou verde. Se três bolinhas forem retiradas do saco, a probabilidade de se obter uma de cada cor será de 20%. Quantas bolinhas de cada cor há no saco? Observe que não especifiquei se as bolinhas são retiradas com ou sem reposição.
Vamos tentar resolver isso considerando a hipótese de reposição. Sejam r, b e g o número de bolinhas vermelhas, azuis e verdes, respectivamente. Então, a probabilidade de retirar uma bolinha de cada cor seria 6*(r/100)*(b/100)*(g/100). Igualando isso a 0,2, podemos dizer:
6*(r/100)*(b/100)*(g/100) = 0,2
6*r*b*g = 200000
6 não divide 200.000 exatamente. Portanto, não há soluções inteiras possíveis para r*b*g = 33333,333... Assim, podemos descartar a possibilidade de sorteio com reposição.
Em seguida, vamos tentar a hipótese "sem reposição". Nesse caso, a probabilidade de retirar um item de cada cor é r*b*g/combin(100,3) = 0,2. Tentando resolver isso...
r*b*g/161700 = 0,2
r*b*g = 32340
A fatoração em números primos de 32340 é 2*2*3*5*7*7*11.
Precisamos distribuir esses fatores entre r, b e g, mantendo r+b+g=100. Por exemplo, poderíamos tentar:
r = 2*3*5 = 30
b = 2*11 = 22
g = 7*7 = 49
Embora essas equações utilizem corretamente todos os fatores primos, r+b+g = 101, portanto não é uma solução válida.
Receio que tenha tido que escrever um programa de força bruta com repetição para obter a solução de r, b e g com valores de 21, 35 e 44, em qualquer ordem.
A seguinte pergunta nos foi enviada pelo Riddler Express .
Vamos assumir as regras da NFL. Considere a seguinte situação:
- O time vermelho está perdendo por 14 pontos no final do jogo.
- A equipe Vermelha terá mais duas posses de bola.
- A equipe Azul não terá mais nenhuma posse de bola.
- Vamos ignorar os field goals e safeties, já que o time Vermelho precisa marcar dois touchdowns para ter chances de vencer.
- Se o jogo for para a prorrogação, cada equipe terá 50% de chance de vencer. O jogo não pode terminar empatado.
- A probabilidade de converter um chute de um ponto após um touchdown é de 100%.
- A probabilidade de realizar uma conversão de dois pontos é p.
Em que valor de p a equipe vermelha deveria ficar indiferente entre chutar e tentar uma conversão de dois pontos após o primeiro touchdown (agora perdendo por 8 pontos)?
Seja p o ponto de indiferença entre tentar a conversão de dois pontos e o chute.
Se a primeira tentativa de conversão de dois pontos for bem-sucedida, o time vermelho poderá chutar a bola pela segunda vez e vencer.
Se a primeira tentativa de conversão de dois pontos falhar, o time vermelho deverá tentar novamente após o segundo touchdown e, em seguida, vencer a partida na prorrogação.
A probabilidade de vencer, tentando a conversão de dois pontos após o primeiro touchdown, é p + (1-p)*p/2. Igualamos isso à probabilidade de 50% de vencer chutando após o primeiro touchdown e resolvemos para p.
p + (1-p)*p/2 = 1/2
2p + (1-p)*p = 1
3p - p^2 = 1
p² - 3p + 1 = 0
Usando a fórmula quadrática, resolva para p:
p = (3 +/- sqrt(5))/2
Optamos pela alternativa negativa, para manter p entre 0 e 1, obtendo p = (3-sqrt(2))/2 ≈ 0,381966011250105
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Na coluna anterior "Pergunte ao Mago" , você foi questionado sobre o número esperado de lançamentos para se obter um total de 12 com dois dados, duas vezes seguidas. Aproveitando o assunto, vi que alguém no fórum afirma ter presenciado 18 "yo" consecutivos (total de 11) na mesa de craps. Qual é o número esperado de lançamentos necessários para que isso aconteça?
Aqui está minha solução (PDF).
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
A resposta exata foi encontrada com a ajuda do WizCalc .
Um campo gramado tem a forma de um círculo com raio de 100 m e é cercado por uma cerca circular. Uma cabra está presa por uma corrente a um gancho, em um ponto fixo da cerca. Para evitar que a cabra engorde demais, o fazendeiro quer garantir que ela só consiga alcançar metade da grama do campo. Qual deve ser o comprimento da corrente?
A título de ilustração, o círculo representa o campo gramado. O "S" representa o local onde a corrente está fixada na borda do campo. A parte amarela do círculo indica o alcance da cabra. A área verde está além do alcance da corrente. O objetivo é posicionar a corrente na distância correta para que as porções verde e amarela fiquem iguais.
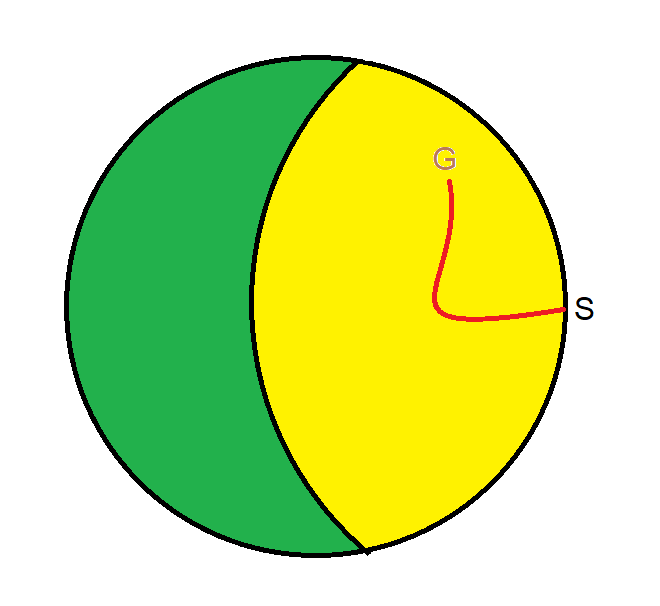
Consulte o diagrama a seguir para resolver este problema.
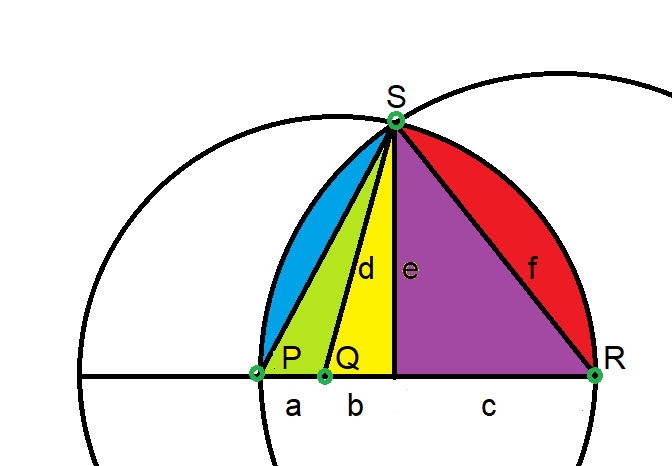
O ponto Q é o centro do círculo gramado. A corrente da cabra está presa ao ponto R. A cabra consegue alcançar todas as regiões coloridas, incluindo sua imagem espelhada abaixo da linha PR.
Sabe-se que o raio do círculo gramado é 100, portanto b + c = d = 100.
A maneira que vou encontrar para resolver isso é definir tudo em termos de b. Depois, vou ajustar os valores de b até obter o resultado desejado, em que a cabra consiga comer metade da grama.
Vamos começar resolvendo para e em função de b. Observando o triângulo com lados b, d e e e usando o teorema de Pitágoras:
b² + e² = d²
b² + e² = 10000
e = sqrt(10000 - b^2)
Em seguida, vamos resolver a equação para f em função de b. Lembre-se, já sabemos que b + c = 100, então c = 100 - b. Usando o Teorema de Pitágoras:
c² + e² = f²
(100-b)^2 + (10000 - b^2) = f^2
f ^ 2 = 10.000 - 200b + b ^ 2 + 10.000 - b ^ 2
f² = 20000 - 200b
f^2 = 100*(200 - 2b)
f = 10*sqrt(200-2b)
Em seguida, vamos calcular a área do triângulo QRS:
QRS = (1/2)*100*e = 50*sqrt(10000 - b^2)
Em seguida, vamos calcular a área da fatia de grama recortada pelo ângulo quadrado:
tan(SQR) = e/b = sqrt(10000-b^2)/b.
fatia SQR = atan(sqrt(10000-b^2)/b)
A área vermelha é igual à fatia SQR menos o triângulo QRS = 5000*atan(sqrt(10000-b^2)/b) - (1/2)*100*e = 50*sqrt(10000 - b^2).
Em seguida, vamos encontrar a área azul + verde + amarela + roxa. Para isso, precisamos encontrar o ângulo QRS.
tan(QRS) = e/c = sqrt(10000-b^2)/(100-b)
ângulo QRS = atan(sqrt(10000-b^2)/(100-b)).
Somando a isso a área vermelha, temos metade da área total que a cabra pode comer:
atan(sqrt(10000-b^2)/(100-b)) + 50*sqrt(10000 - b^2).
Para a parte abaixo da linha PR, dobre esse valor para obter a área total:
2*atan(sqrt(10000-b^2)/(100-b)) + 100*sqrt(10000 - b^2).
A área total da região gramada é de 10.000*pi.
Agora, basta ajustar o valor de b até obter uma área que a cabra possa comer igual a 5.000 * pi. A função Atingir Meta do Excel é ótima para problemas como este. Como alguém conseguia fazer alguma coisa antes das planilhas, eu não faço ideia.
Usando este método, você descobrirá que b = 32,867402.
A partir daí podemos obter f = comprimento da corrente = 115,8728598 metros.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Qual é a sua palavra inicial recomendada no Wordle ?
Para responder a essa pergunta, primeiro analisei a frequência de cada letra em cada posição, com base na lista de soluções permitidas no Wordle .
Frequência de letras no Wordle
| Carta | Posição 1 | Posição 2 | Posição 3 | Posição 4 | Posição 5 | Total |
|---|---|---|---|---|---|---|
| UM | 141 | 304 | 307 | 163 | 64 | 979 |
| B | 173 | 16 | 57 | 24 | 11 | 281 |
| C | 198 | 40 | 56 | 152 | 31 | 477 |
| D | 111 | 20 | 75 | 69 | 118 | 393 |
| E | 72 | 242 | 177 | 318 | 424 | 1233 |
| F | 136 | 8 | 25 | 35 | 26 | 230 |
| G | 115 | 12 | 67 | 76 | 41 | 311 |
| H | 69 | 144 | 9 | 28 | 139 | 389 |
| EU | 34 | 202 | 266 | 158 | 11 | 671 |
| J | 20 | 2 | 3 | 2 | 0 | 27 |
| K | 20 | 10 | 12 | 55 | 113 | 210 |
| eu | 88 | 201 | 112 | 162 | 156 | 719 |
| M | 107 | 38 | 61 | 68 | 42 | 316 |
| N | 37 | 87 | 139 | 182 | 130 | 575 |
| O | 41 | 279 | 244 | 132 | 58 | 754 |
| P | 142 | 61 | 58 | 50 | 56 | 367 |
| P | 23 | 5 | 1 | 0 | 0 | 29 |
| R | 105 | 267 | 163 | 152 | 212 | 899 |
| S | 366 | 16 | 80 | 171 | 36 | 669 |
| T | 149 | 77 | 111 | 139 | 253 | 729 |
| Você | 33 | 186 | 165 | 82 | 1 | 467 |
| V | 43 | 15 | 49 | 46 | 0 | 153 |
| C | 83 | 44 | 26 | 25 | 17 | 195 |
| X | 0 | 14 | 12 | 3 | 8 | 37 |
| Y | 6 | 23 | 29 | 3 | 364 | 425 |
| Z | 3 | 2 | 11 | 20 | 4 | 40 |
Em seguida, examinei todas as palavras na lista de soluções do Wordle com cinco letras distintas e as pontuei de acordo com a tabela de frequência de letras acima. Atribui dois pontos para uma correspondência na posição correta e um ponto para uma correspondência em uma posição incorreta. Depois, ordenei a lista, que você vê abaixo.
Melhores palavras iniciais no Wordle
<!--/box-title-->| Classificação | Palavra | centrado">Pontos|
|---|---|---|
| 1 | Olhar fixamente | 5835 |
| 2 | Surgiu | 5781 |
| 3 | Ardósia | 5766 |
| 4 | Elevação | 5721 |
| 5 | Surgir | 5720 |
| 6 | Mais são | 5694 |
| 7 | Laço | 5691 |
| 8 | Irritado | 5682 |
| 9 | Obsoleto | 5665 |
| 10 | Caixa | 5652 |
| 11 | Rastrear | 5616 |
| 12 | Mais tarde | 5592 |
| 13 | Compartilhar | 5562 |
| 14 | Loja | 5547 |
| 15 | Susto | 5546 |
| 16 | Alterar | 5542 |
| 17 | Guindaste | 5541 |
| 18 | Alerta | 5483 |
| 19 | Lacrimosa | 5479 |
| 20 | refogar | 5475 |
| 21 | Atender | 5460 |
| 22 | Poupar | 5457 |
| 23 | Sozinho | 5452 |
| 24 | Troca | 5449 |
| 25 | Ronco | 5403 |
| 26 | Grelha | 5403 |
| 27 | Xisto | 5392 |
| 28 | Ao menos | 5390 |
| 29 | Roubou | 5377 |
| 30 | Escala | 5376 |
| 31 | Reagir | 5376 |
| 32 | Blare | 5368 |
| 33 | Analisar | 5351 |
| 34 | Brilho | 5340 |
| 35 | Expiar | 5338 |
| 36 | Aprender | 5324 |
| 37 | Cedo | 5320 |
| 38 | Inclinado | 5307 |
| 39 | Mais pálido | 5285 |
| 40 | Sinalizador | 5280 |
| 41 | Corredor | 5280 |
| 42 | Costa | 5274 |
| 43 | Roubar | 5268 |
| 44 | Instante | 5267 |
| 45 | Pontuação | 5258 |
| 46 | Claro | 5258 |
| 47 | Anciã | 5253 |
| 48 | Pedra | 5253 |
| 49 | Coração | 5252 |
| 50 | Perdedor | 5251 |
| 51 | Cone | 5248 |
| 52 | Odiador | 5243 |
| 53 | Revezamento | 5241 |
| 54 | Placa | 5240 |
| 55 | Adoro | 5239 |
| 56 | Molho | 5236 |
| 57 | Mais seguro | 5235 |
| 58 | Estrangeiro | 5233 |
| 59 | Casta | 5232 |
| 60 | Cisalhamento | 5231 |
| 61 | Enfardadeira | 5230 |
| 62 | Sirene | 5226 |
| 63 | Canoa | 5215 |
| 64 | Condado | 5213 |
| 65 | Renal | 5210 |
| 66 | Camada | 5206 |
| 67 | Domador | 5200 |
| 68 | Grande | 5196 |
| 69 | Pérola | 5196 |
| 70 | Rota | 5194 |
| 71 | Suporte | 5192 |
| 72 | Fatiar | 5178 |
| 73 | Estágio | 5171 |
| 74 | Prosa | 5170 |
| 75 | Esporo | 5169 |
| 76 | Rouse | 5166 |
| 77 | Graça | 5164 |
| 78 | Solar | 5152 |
| 79 | Suíte | 5150 |
| 80 | Assar | 5145 |
| 81 | Cerveja | 5130 |
| 82 | Avião | 5129 |
| 83 | Chuteira | 5129 |
| 84 | Tratado | 5128 |
| 85 | Lança | 5126 |
| 86 | Ótimo | 5126 |
| 87 | Auxiliar | 5123 |
| 88 | Tropo | 5116 |
| 89 | Pináculo | 5108 |
| 90 | Piso | 5107 |
| 91 | Escravo | 5097 |
| 92 | Fechar | 5090 |
| 93 | Lança | 5090 |
| 94 | Limpar | 5088 |
| 95 | Causa | 5087 |
| 96 | Propenso | 5087 |
| 97 | Drone | 5082 |
| 98 | Barulho | 5079 |
| 99 | Crista | 5073 |
| 100 | Sóbrio | 5068 |
Então, aí está, a palavra inicial que recomendo, e que eu uso, é OLHAR FINALMENTE.
O que é i^i
Aqui está minha solução (PDF).
Você deseja jogar um jogo que requer dois dados comuns de seis lados. Infelizmente, você perdeu os dados. No entanto, você tem nove fichas, que pode marcar como quiser. O jogador deve escolher duas fichas aleatoriamente dentre as nove, sem reposição, e somar os valores das duas fichas.
Marque os cartões da seguinte forma:
1 a 0,5
1 a 1,5
2 a 2,5
1 @ 3,5
2 a 4,5
1 @ 5,5
1 @ 6,5
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
É verdade que, ao lançar uma moeda honesta, é mais provável que a face que estava inicialmente voltada para cima fique voltada para cima?
As evidências sugerem que isso é verdade!
Persi Diaconis e Susan Holmes, da Universidade de Stanford, registraram 10.000 lançamentos de moeda. A moeda caiu com a face para cima na mesma posição inicial em 50,8% das vezes (fonte: The Fifty-one Percent Solution, do boletim informativo What's Happening in the Mathematical Sciences, da American Mathematical Society). A probabilidade de uma proporção tão alta ou maior é de 5,48%.
Para provar isso matematicamente, assumi que o número real de rotações de uma moeda seguia a distribuição de Poisson. Mais especificamente, se o número médio de rotações fosse m, então a probabilidade de ocorrerem exatamente n rotações seria exp(-m)*m^n/n!. Para ilustrar a distribuição de Poisson, o gráfico a seguir mostra a probabilidade de ocorrerem de 0 a 25 rotações, dada uma média de 10.
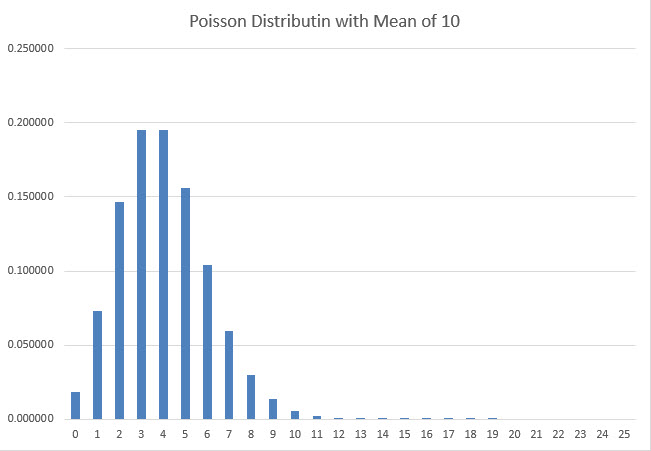
A razão pela qual escolhi a hipótese de Poisson é que ela segue uma forma próxima à de uma curva em forma de sino para médias suficientemente grandes, e o resultado real nunca pode ser inferior a zero.
Em seguida, calculei a probabilidade de um número par de meias-revoluções (resultando no mesmo lado da face inicial para cima) para várias médias de meias-revoluções. A tabela a seguir mostra os resultados para médias de 0,5 a 5,0.
Probabilidade de um número par ou ímpar de revoluções
| Revoluções Médias | Total par | Total Ímpar |
|---|---|---|
| 0,5 | 0,567667642 | 0,432332358 |
| 1 | 0,509157819 | 0,490842181 |
| 1,5 | 0,501239376 | 0,498760624 |
| 2 | 0,500167731 | 0,499832269 |
| 2,5 | 0,500022700 | 0,499977300 |
| 3 | 0,500003072 | 0,499996928 |
| 3,5 | 0,500000416 | 0,499999584 |
| 4 | 0,500000056 | 0,499999944 |
| 4.5 | 0,500000008 | 0,499999992 |
| 5 | 0,500000001 | 0,499999999 |
Então, comecei a me perguntar por que a probabilidade de um número par era sempre maior que 50%. Acontece que a probabilidade de um número par, dada uma média de m, pode ser expressa como 0,5 + e^(-2m)/2. Como e elevado a qualquer potência deve ser positivo, a probabilidade de um número par de revoluções também é positiva.
Você pode ver a minha demonstração desta fórmula aqui .
Resolva para x:
9x + 12x = 16x
Aqui está minha solução (PDF).
Essa questão foi levantada e discutida no meu fórum, Wizard of Odds .
Este problema foi inspirado pelo vídeo "Uma Questão Exponencial Difícil" .
Seu escritório com 100 funcionários realiza uma troca de presentes de Amigo Secreto. A ideia é escrever o nome de cada pessoa em pedaços de papel individuais, colocá-los em um chapéu e todos sorteiam um nome aleatoriamente para dar um presente.
A questão é: quantos circuitos fechados haverá, em média?
Exemplo de um ciclo fechado de tamanho 4: Gordon dá para Don, Don dá para Jon, Jon dá para Nathan, e Nathan dá para Gordon.
Desenhar o próprio nome seria um laço fechado de tamanho 1.
Suponha que haja apenas um funcionário que compareça à festa do Amigo Secreto. Obviamente, ele escolherá a si mesmo, fechando assim o ciclo.
Então, uma segunda funcionária chega atrasada e pede para participar. Entregam a ela uma lista com os nomes dos dois funcionários. Há 50% de chance de ela escolher o funcionário 1 e 50% de chance de escolher a si mesma. Se ela escolher o funcionário 1, ela pode ser incluída no esquema dele, onde ela compra para o funcionário 1 e ele compra para ela. Então, agora estamos com 1 + 0,5 * 1 = 1,5.
Então, uma terceira funcionária chega atrasada e pede para participar. Entregam a ela uma lista com os nomes dos três funcionários. Há 2/3 de chance de ela escolher o funcionário 1 ou 2 e 1/3 de chance de escolher a si mesma. Se ela escolher o funcionário 1 ou 2, ela pode ser incluída no esquema, onde ela compra para o funcionário que escolheu e quem deveria comprar para esse funcionário agora compra para o terceiro. Então, agora estamos com 1,5 + (1/3) = 11/6.
Então, uma quarta funcionária chega atrasada e pede para participar. Entregam a ela uma lista com os nomes dos quatro funcionários. Há 3/4 de chance de ela escolher os funcionários de 1 a 3 e 1/4 de chance de escolher a si mesma. Se ela escolher os funcionários de 1 a 3, então ela pode ser incluída no esquema, onde ela compra para o funcionário que escolheu e quem antes deveria comprar para esse funcionário agora compra para o quarto. Então, agora estamos com 11/6 + (1/4) = 25/12.
Continue fazendo isso e a resposta final será 1/1 + 1/2 + 1/3 + ... + 1/100 =~ 5,187377518.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Considere um semicírculo de raio 1 com dois retângulos empilhados em seu interior. Qual é a área máxima combinada dos dois retângulos?
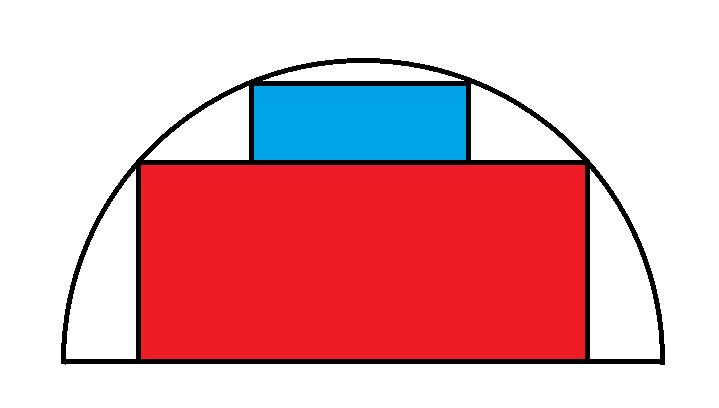
Segue minha solução completa (PDF).
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Ignore gêmeos idênticos e assuma que cada criança tem 50% de chance de nascer menino ou menina. Se crianças forem selecionadas aleatoriamente de famílias com um tamanho específico de 2 a 5 pessoas, qual é a probabilidade de um menino ou menina ter uma irmã?
Curiosamente, a probabilidade é a mesma para ambos os sexos, independentemente do tamanho da família.
Vamos analisar famílias de três pessoas, por exemplo. Aqui estão as oito maneiras possíveis de organizar meninos e meninas, em relação à ordem:
BBB
BBG
BGB
BGG
GBB
GBG
GGB
GGG
Se você escolher qualquer garota aleatoriamente da lista acima, verá que, das 12 garotas, 9 têm irmãs. O mesmo acontece com os 12 garotos: 9 têm irmãs. Portanto, a probabilidade é 9/12 = 3/4.
A fórmula geral para a probabilidade de qualquer criança ter uma irmã, onde o número de crianças é n, é 1-(1/2) n-1 .
Aqui está a probabilidade de ter uma irmã em relação ao número total de filhos na família:
- 1: 0
- 2: 1/2
- 3: 3/4
- 4: 7/8
- 5: 15/16
- 6: 31/32
Alternativamente, faz sentido que a probabilidade seja a mesma para meninos e meninas. O sexo dos seus irmãos não está correlacionado com o seu sexo. Portanto, apenas o tamanho da família importa, não o seu próprio sexo.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
No episódio 4 da 37ª temporada de Survivor, houve um desafio em que quatro peças de quebra-cabeça podiam ser organizadas tanto em um quadrado quanto em um triângulo equilátero. Quais seriam as dimensões exatas das peças para que isso funcionasse?
 |  |
Primeiro, vamos fazer um diagrama adequado e rotulá-lo.
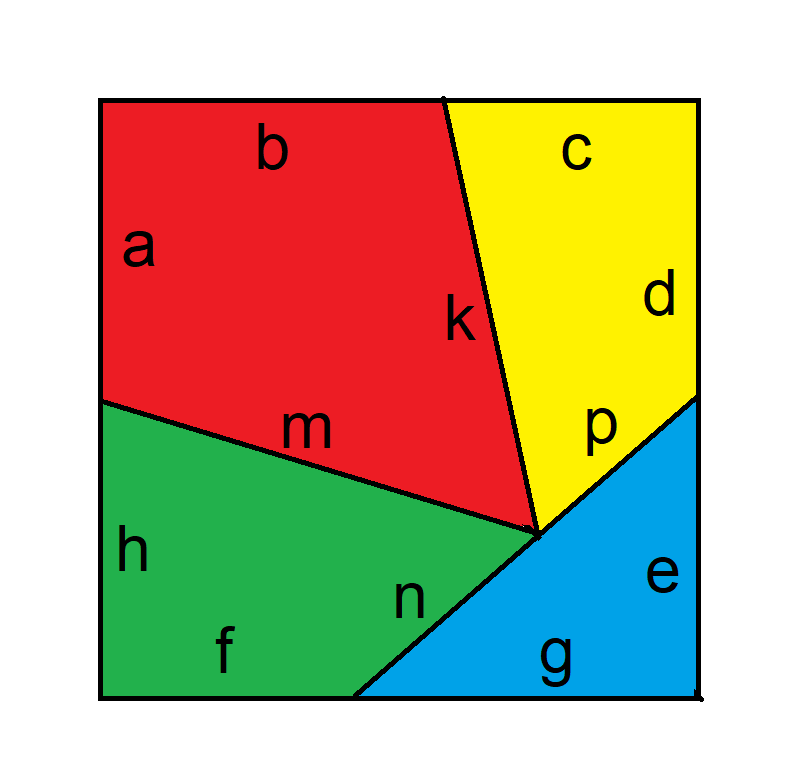
A seguir, apresentamos o diagrama do triângulo resolvido.
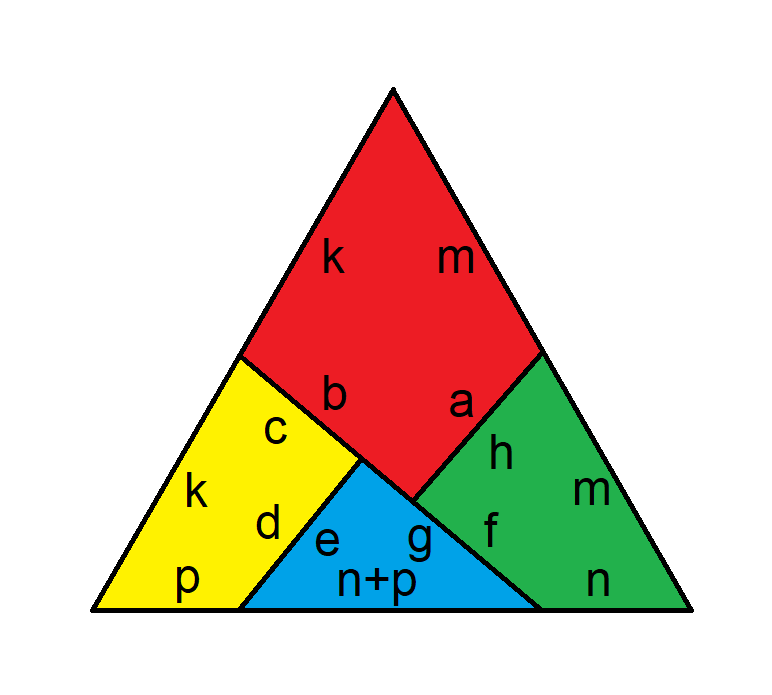
Em seguida, supondo que os lados do quadrado tenham comprimento 1, aqui está o comprimento de cada letra no diagrama acima.
a = d = e = h = 1/2
b = g = QUADRADO((4-QUADRADO(3))/(4*QUADRADO(3))) =~ 0,572145321740575
c = f = 1-QUADRADO((4-QUADRADO(3))/(4*QUADRADO(3))) =~ 0,427854678259425
k = m = 1/SQRT(SQRT(3)) =~ 0,759835685651592
n = (3-QUADRADO(4*QUADRADO(3)-3))/(2*QUADRADO(QUADRADO(3))) =~ 0,386767938902275
p = (QUADRADO(4*QUADRADO(3)-3)-1)/(2*QUADRADO(3))) =~ 0,373067746749317
Finalmente, aqui está minha solução completa (PDF).
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Tenho certeza de que você é fã de The Big Bang Theory. Uma das minhas cenas favoritas é a do jogo de Pedra, Papel e Tesoura com o Spock Lagarto. É como um jogo de Pedra, Papel e Tesoura com cinco símbolos, com as seguintes regras:
- Papel cobre rocha
- Pedra esmaga lagarto
- Lagarto envenena Spock
- Spock esmaga tesouras
- Tesoura corta papel
- Lagarto come papel Spock vaporiza rocha
- Tesoura decapita lagarto
- Artigo refuta Spock
- Pedra esmaga tesouras
Minha pergunta é: é possível adicionar mais símbolos, de forma que todos os lados tenham as mesmas chances contra um jogador aleatório?
Sim, eu também adoro essa cena! Aqui está um vídeo dela no YouTube .
Você precisa de um número ímpar de símbolos. Em teoria, você poderia ter um número par, mas aí teria que criar regras em que certos pares de símbolos diferentes resultassem em empate. Não, queremos um jogo decisivo em que os únicos empates ocorram se ambos os jogadores jogarem o mesmo símbolo.
Uma solução é especialmente elegante e fácil de explicar com um número primo de símbolos. Permita-me explicar com sete símbolos, como exemplo. Vamos rotular os símbolos de A a G e representá-los em um círculo, no diagrama a seguir.
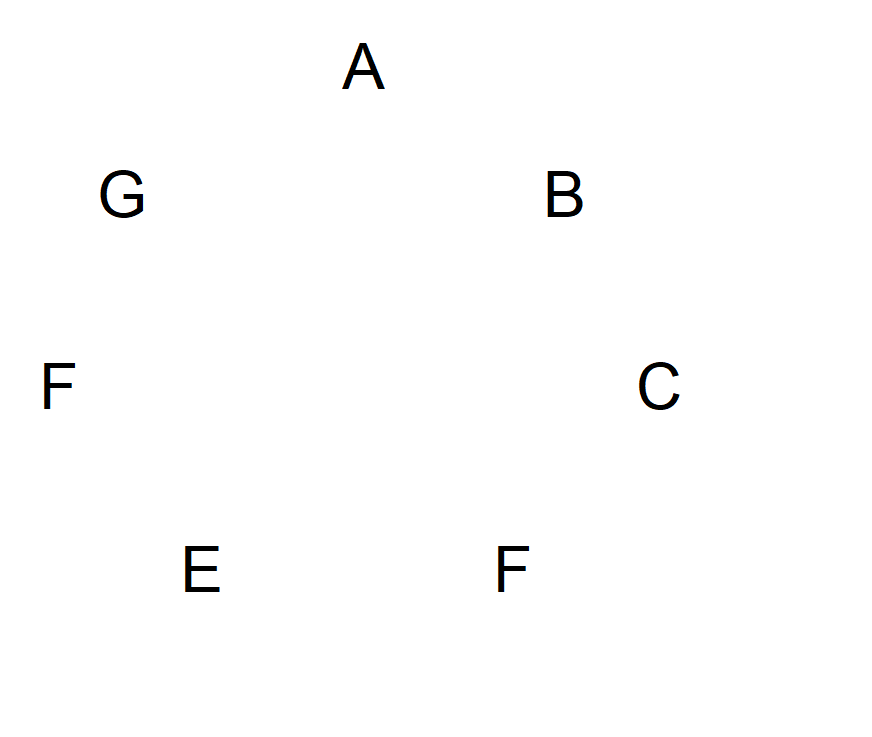
Em seguida, comece com A e desenhe uma seta para o próximo símbolo no sentido horário. A seta deve apontar para o símbolo que está entre esses dois. Imagine que esse símbolo está sendo atingido por uma flecha. Continue no sentido horário até retornar a A. O diagrama não ficará assim:
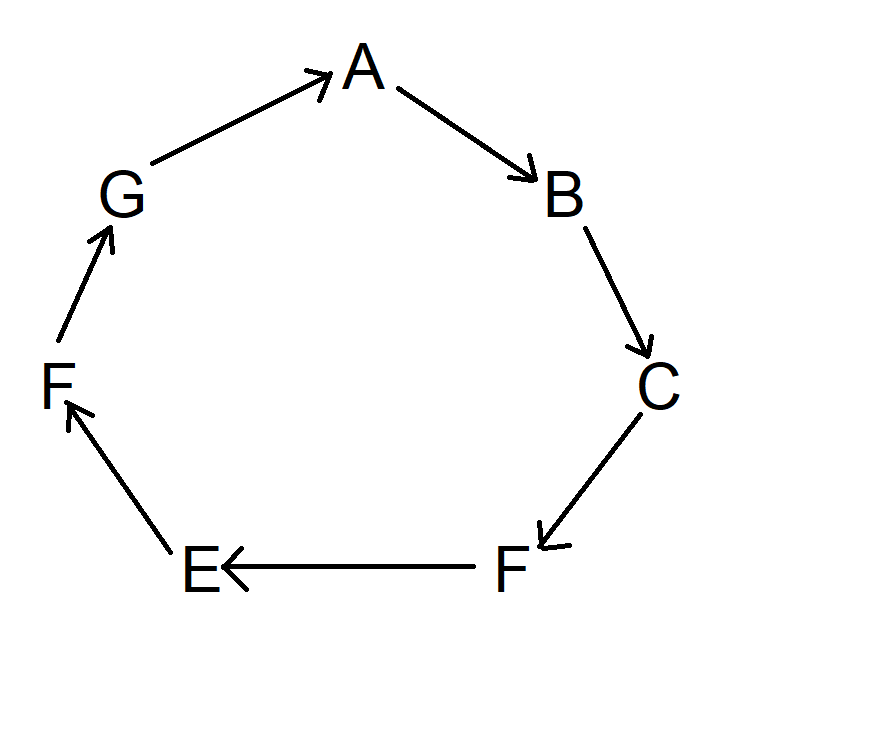
Em seguida, faça o mesmo, mas avance dois símbolos no sentido horário, começando em A. Na verdade, você pode começar em qualquer lugar que desejar. O diagrama agora se parece com isto:
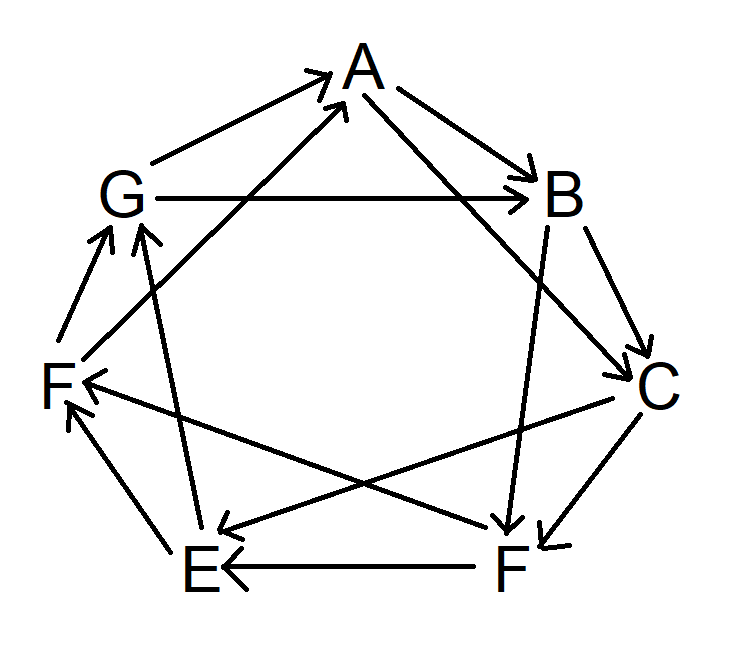
Por fim, faça o mesmo, mas pule três símbolos no sentido horário. O diagrama agora ficará assim:
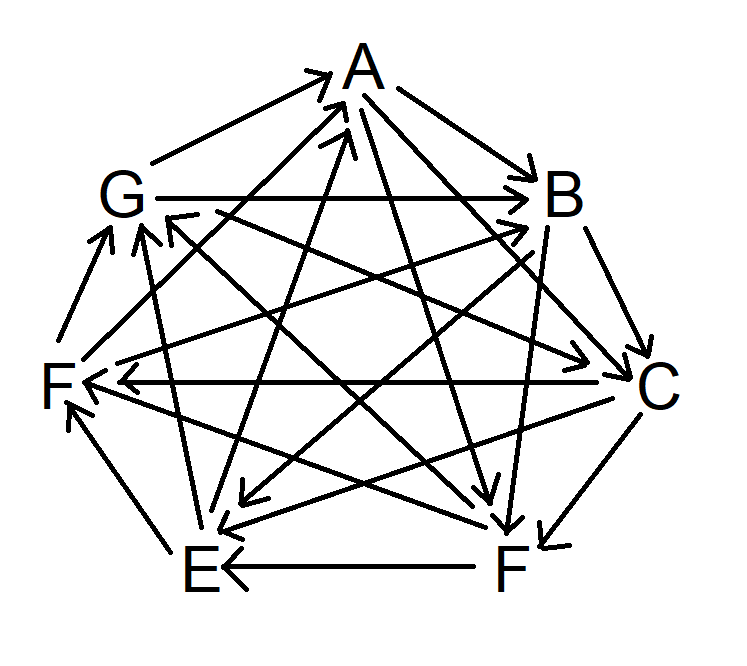
Observe que, neste ponto, cada símbolo vence outros três símbolos e é vencido por outros três símbolos diferentes.
Este método funciona para qualquer número primo de símbolos, pois, ao retornar ao símbolo original, você já terá passado por todos os símbolos. Para n símbolos, você terá que repetir esse processo (n-1)/2 vezes.
É possível criar um jogo equilibrado com qualquer número ímpar de símbolos, mas, às vezes, você retornará ao símbolo original muito rapidamente. Quando isso acontecer, você terá que fazer novos loops começando pelos símbolos que perdeu.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Você embaralha um conjunto padrão de dominós (28 peças) e retira uma peça aleatoriamente. Com cuidado, você descobre uma das faces para revelar um 6. Qual é a probabilidade de que essa peça seja o 6 duplo?
Para quem não está familiarizado com dominós, uma peça de dominó tem dois lados, cada um com um número de 0 a 6. Um conjunto consiste em uma peça de cada tipo de dominó possível. Isso corresponde a todas as combin(7,2)=21 maneiras de escolher números, sem reposição, dentre os 7 números possíveis, mais todas as 7 maneiras de ter ambos os números no mesmo lado.
Aqui estão todas as 28 sequências: 0-0, 0-1, 0-2, 0-3, 0-4, 0-5, 0-6, 1-1, 1-2, 1-3, 1-4, 1-5, 1-6, 2-2-2, 2-3, 2-4, 2-5, 2-6, 3-3, 3-4, 3-5, 3-6, 4-4, 4-5, 4-6, 5-5, 5-6, 6-6.
Feita essa explicação, aqui estão a resposta e a solução.
Uma maneira simples de reformular a pergunta é: qual a probabilidade de uma peça de dominó escolhida aleatoriamente ter o mesmo número em ambos os lados? A resposta é simplesmente 7/28 = 1/4.
Você pode dizer que a resposta deveria ser 1/7, porque o outro lado poderia ser qualquer um dos sete números possíveis. É verdade que poderia ser qualquer um dos sete números, mas eles não são todos igualmente prováveis. O dominó 6-6 deve ser contado duas vezes, porque tem dois lados com o número seis. Portanto, o outro lado poderia ser qualquer um dos dois seis e há oito seis no total no conjunto. Assim, a resposta é 2/8 = 1/4.
Esta pergunta foi feita e discutida no meu fórum, Wizard of Vegas . A pergunta é dedicada à memória de Alan Mendelson.
Alan e Bob decidem jogar tênis até que um deles ganhe duas partidas seguidas. A probabilidade de Alan ganhar qualquer partida é de 2/3. Qual é a probabilidade de Alan ganhar o torneio?
Alan e Bob decidem jogar tênis até que um deles ganhe duas partidas seguidas. A probabilidade de Alan ganhar qualquer partida é de 2/3. Qual é a probabilidade de Alan ganhar o torneio?
A seguir, apresentamos a solução de geração para qualquer probabilidade de Alan vencer uma partida individual.
Seja p = probabilidade de a vencer.
Seja a = probabilidade de Alan vencer o torneio depois de Alan vencer a última partida.
Seja b a probabilidade de Alan vencer o torneio depois de Bob vencer a última partida.
(1) a = p + (1-p)*b
(2) b = p*a
Substituindo a equação (2) na equação (1):
a = p + (1-p)*pa
a = p + pa - p 2 *a
a - pa + p 2 *a = p
a(1-p+p 2 ) = p
(3) a = p/(1-p+p 2 )
Substituindo a equação (3) na equação (2):
b = p 2 /(1-p+p 2 )
O primeiro jogo determinará se a probabilidade de um jogador vencer o torneio é a ou b:
resposta = pa + (1-p)b
= p 2 /(1-p+p 2 ) + (1-p)*p 2 /(1-p+p 2 )
= (2a 2 -a 3 )/(a 2 -a+1)
Substituindo a = 2/3, obtemos uma probabilidade de ganhar o torneio de 16/21.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Você tem uma escada de 1,5 metro (5 pés). Você deseja encostá-la na parede o mais alto possível. No entanto, há uma caixa de 0,028 m x 0,028 m x 0,028 m³ (1 pé cúbico x 1 pé cúbico x 1 pé cúbico) sobre a qual você precisa colocar a escada. Não, você não pode mover a caixa. Qual é a altura máxima que o topo da escada pode alcançar?
Aqui está minha solução (PDF).
Em que valor x 1/x atinge o máximo?
A resposta é e =~ 2,71828182845905.
Ali, o valor de e^(1/e) =~ 1,44466786100977.
Aqui está minha solução (PDF).
Em 1944, os jornais notaram esta incrível coincidência:
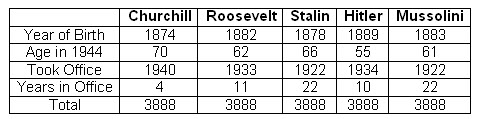
Será isso uma grande coincidência ou há algum artifício matemático envolvido?
É um artifício matemático e a base de um truque de mágica conhecido.
Para todas as pessoas vivas em 1944, a soma da sua idade (após o aniversário) e do seu ano de nascimento era 1944. Pense nisso. Se você tinha x anos, então você nasceu em 1944-x. A soma é x + (1944-x) = 1944.
É a mesma coisa que os "anos no cargo" em 1944. Se você esteve no cargo por y anos, então você deve ter começado em 1944-y. y + (1944-y) = 1944.
A soma de 1944 + 1944 = 3.888. Funciona sempre.
Para transformar isso em um truque de mágica que funcione em 2023, é preciso somar os seguintes quatro elementos:
- Ano de nascimento deles
- Quantos anos eles completarão este ano?
- Ano em que ocorreu algum evento significativo (como o nascimento do primeiro filho).
- Aniversário desse evento significativo este ano.
A soma será sempre 2023 + 2023 = 4046.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .