Texas Hold'em - Probabilidade - Geral
Qual a probabilidade de um jogador receber duas quadras e um straight flush em uma partida de Texas Hold'em com dez jogadores em 50 mãos?
A probabilidade de uma quadra em sete cartas é 0,00168067, e a probabilidade de uma sequência de flush é 0,00027851. Se x é a probabilidade de uma quadra e y é a probabilidade de uma sequência de flush, então a probabilidade que você procura é combin(50,2)*48* x² *y*(1-xy) ⁴⁷ . A resposta é 0,0000421845, ou 1 em 23.705.
Quais são as probabilidades estatísticas de se obter um flush no Texas Hold'em? É mais fácil para um jogador obter um flush no Seven-Card Stud ou no Hold'em?
Você pode consultar minha seção sobre probabilidades no pôquer para ver que a probabilidade é de 3,03%. As probabilidades são as mesmas tanto no Texas Hold'em quanto no Seven-Card Stud.
Quais são as chances de fazer um royal flush no Texas Hold'em no river?
Para quem não sabe, o river é a quinta e última carta comunitária no Texas Hold'em. O jogador deve formar a melhor mão de pôquer possível com suas duas cartas e as cinco cartas comunitárias. Então, você está perguntando qual a probabilidade de um jogador formar um Royal Flush com sete cartas, e que a sétima carta distribuída faça parte desse Royal Flush. A probabilidade de formar um Royal Flush de 5 cartas com 7 cartas, antes de considerar as cartas comunitárias, é 4*combin(47,2)/combin(52,7) = 4324/133784560, ou 1 em 30940. A probabilidade de a sétima carta fazer parte do Royal Flush é 5/7. Portanto, a probabilidade final é 21620/936491920, ou 1 em 43316.
No Texas Hold'em, qual a probabilidade de formar uma sequência interna com um ou dois espaços na mão até a quinta carta, começando pelo flop?
Para benefício dos meus leitores, esta questão pergunta qual é a probabilidade de preencher uma lacuna de uma ou duas cartas dentro de uma sequência com mais duas cartas, restando 47 cartas no baralho. Com uma lacuna, a probabilidade é 1 - combin(43,2)/combin(47,2) = 0,164662. Com duas lacunas, a probabilidade é 42/ combin(47,2) = 0,0148.
No Texas Hold'em, se as cartas do flop forem todas do mesmo naipe, qual é a probabilidade de um determinado jogador ter mais duas cartas do mesmo naipe?
Restam 10 cartas do mesmo naipe e 49 no baralho. Portanto, a probabilidade é combin(9,2)/combin(49,2) = 36/1176 = 0,0306.
As probabilidades para as diferentes mãos são as mesmas no Texas Hold'em e no Seven-Card Stud, ou são diferentes de alguma forma devido às cartas comunitárias? Poderia explicar o porquê?
Sim, as probabilidades são as mesmas. Sete cartas aleatórias dentre 52 têm as mesmas chances, independentemente de como forem retiradas do baralho ou com quem você as compartilhar.
Nas duas primeiras cartas, você pode me dizer qual a probabilidade de receber 7 mãos de Ás-Rei ou melhor no Hold'em em 35 mãos?
A probabilidade de receber um ás/rei é (8/52)*(4/51) = 0,012066. A probabilidade de receber qualquer par é (3/51) = 0,058824. Portanto, a probabilidade de um par ou melhor é 0,07089. A probabilidade de receber exatamente sete mãos de ás/rei ou melhor é combin(35,7)*(0,07089)^7*(1-0,07089)^28 = 0,00772. Para calcular a probabilidade de 7 ou mais, teríamos que analisar um total de 7 a 35, um por vez. Isso resulta em 0,010366551.
Como você calcularia a probabilidade de obter um flush de 4 cartas ou melhor no flop no Hold'em, se suas cartas iniciais forem do mesmo naipe?
A probabilidade de obter mais 2 cartas do mesmo naipe é 39*combin(11,2)/combin(50,3) = 0,109439. A probabilidade de obter mais 3 cartas do mesmo naipe é combin(11,3)/combin(50,3) = 0,008418. Portanto, a probabilidade de obter pelo menos mais 2 cartas do mesmo naipe é 0,117857.
Sr. Wizard, antes de mais nada, gostaria de dizer que seu site é fantástico! Venho lendo há algum tempo. Dei uma olhada nas perguntas sobre pôquer e não encontrei esta. Outro site afirma o seguinte: "No Texas Hold'em, a probabilidade de receber um AK pré-flop e acertar um A ou K no river é de 1 em 2 (par)". Isso me parece intuitivamente muito alto. O que você acha? Obrigado novamente!
Obrigado também pelas gentis palavras. Para quem não está familiarizado com Hold'em, esta pergunta é semelhante a perguntar se um jogador recebesse um ás e um rei, mais cinco cartas aleatórias das 50 restantes, qual a probabilidade de ele formar um par com o rei e/ou o ás? Das outras 50 cartas, 44 não são reis nem ases. O número de maneiras de tirar cinco cartas quaisquer dentre as 44 é combin(44,5) = 1.086.088. O número de maneiras de tirar cinco cartas quaisquer dentre as 50 é combin(50,5) = 2.118.760. Portanto, a probabilidade de não formar um par com o ás e/ou o rei é 1.086.088/2.118.760 = 51,26%. Assim, a probabilidade de formar um par é 1 - 51,26% = 48,74%. Isso é bem próximo de 1 em 2.
Qual a probabilidade de dois jogadores terem quadras diferentes no Texas Hold'em?
Entre dois jogadores, há um total de 9 cartas. Estas devem consistir em duas quadras e uma carta única. O número de combinações possíveis é combin(13,2)*44 = 3432. O número total de maneiras de escolher 9 cartas dentre 52 é combin(52,9) = 3.679.075.400. Portanto, a probabilidade de você ter as cartas certas, mas não necessariamente na ordem correta, é 3432/3.679.075.400 = 1 em 1.071.992.
No entanto, o fato de as cartas serem AAAABBBBC não significa que ambos os jogadores terão quadras diferentes. O número de maneiras de organizá-las em uma mão de 5 cartas e duas mãos de 2 cartas é 9!/(5!*2!*2!) = 756. A seguir, estão as maneiras pelas quais essas 9 cartas podem ser distribuídas.
Quatro Combinações de Má Sorte
Jogador 1 | Jogador 2 | Fracasso | Padrões de espelho | Combinações por padrão | Total de combinações |
AA | BB | AABBC | 2 | 72 | |
AA | AB | ABBBC | 4 | 48 | 192 |
AA | AA | BBBBC | 2 | 6 | 12 |
AA | AC | ABBBB | 4 | 12 | 48 |
AA | Colúmbia Britânica | AABBB | 4 | 24 | 96 |
AB | AB | AABBC | 1 | 144 | 144 |
AB | AC | AABBB | 4 | 48 | 192 |
Desses, apenas o primeiro e o quinto grupo resultam em ambos os jogadores tendo uma quadra diferente. Portanto, a probabilidade de um conjunto de cartas AAAABBBBC resultar em duas quadras diferentes é 168/756 = 22,22%.
Portanto, a resposta para sua pergunta é (3432/3.679.075.400)*(168/756) = 1 em 4.823.963. Em termos mais práticos, o Party Poker tem um jackpot de bad beat para uma mão perdedora de quatro oitos. Dado que existem duas quadras, a probabilidade de ambas serem oitos ou maiores é combin(7,2)/combin(13,2) = 21/78 = 26,92%. Assim, a probabilidade de qualquer mão de dois jogadores resultar nesse jackpot de bad beat é de 1 em 17.917.577.
Ontem à noite, um jogador me ofereceu uma aposta paralela no Texas Hold'em. Ele disse que pelo menos uma carta com figura (ou quaisquer três cartas de mesmo valor) apareceria no flop e ofereceu pagamento igual. Eu deveria ter aceitado a aposta?
O número de maneiras de escolher 3 cartas dentre as 40 cartas que não são figuras é (40*39*38)/(1*2*3) = 9880. O número de maneiras de escolher 3 cartas dentre as 52 é (52*51*50)/(1*2*3) = 22100. Portanto, a probabilidade de não receber uma figura é 9880/22100 = 44,71%. Assim, a probabilidade de receber uma figura é 55,29%. O lado dele na aposta tinha uma vantagem de 10,58%.
Em uma partida de Texas Hold'em com 10 jogadores usando um baralho padrão de 52 cartas, após as duas primeiras cartas serem distribuídas para cada jogador, qual a probabilidade de o "flop" (as três cartas seguintes) ser composto inteiramente por cartas do mesmo naipe? Faz diferença se a minha mão tiver duas cartas do mesmo naipe e/ou cada uma de um naipe diferente?
Antes de considerar suas próprias cartas, a probabilidade é 4× combin (13,3)/combin(52,3) = 5,1764706%.
Outra maneira de ver isso é que a probabilidade da segunda carta no flop combinar com a primeira do mesmo naipe é (12/51). A probabilidade da terceira carta no flop combinar com ela é (11/50). (12/51)×(11/50)=5,1764706%.
As probabilidades mudam um pouco se você considerar suas próprias cartas. Se você tiver duas cartas do mesmo naipe, então a probabilidade de um flop do mesmo naipe é pr(flush do mesmo naipe) + pr(flush de naipe diferente) = combin(11,3)/combin(50,3) + 3×combin(13,3)/combin(50,3) = 5,2193878%.
Se você tiver duas cartas de naipes diferentes, então a probabilidade de um flop do mesmo naipe é pr(flush do mesmo naipe em comum) + pr(flush de naipe diferente) = 2×combin(12,3)/combin(50,3) + 2×combin(13,3)/combin(50,3) = 5,1632653%.
Caro gênio, como eu gostaria de ter seu cérebro! De qualquer forma, minha luta com estatística continua. Estou tentando encontrar uma fórmula para calcular a probabilidade de formar um flush no flop, no turn e no river (Texas Hold'em), considerando se minhas cartas iniciais são do mesmo naipe ou não. Tentei C(50,2) / C(47,5), mas não funcionou para um par do mesmo naipe no river... Eu deveria ter prestado mais atenção na escola! Obrigado! Seu maior fã
Obrigado pelas palavras gentis, mas não sou tão inteligente assim. Há alguns anos, fiz o exame de admissão da Mensa e não fiquei entre os 2% melhores. Ainda estou chateado por terem se recusado a me dizer o quão bem eu me saí. No dia 13 de janeiro, haverá testes para o Jeopardy em Las Vegas, para os quais já tenho um horário marcado, e tenho certeza de que também vou me dar mal. Enfim, para responder à sua pergunta, aqui está:
Com cartas fechadas do mesmo naipe:
Flush após flop: combin (11,3)/combin(50,3) = 165/19600 = 0,842%.
Flush após a virada: (combin(11,2)*39/combin(50,3))*(9/47) = 2,096%.
Descarga após rio: (combin(11,2)*combin(39,2)/combin(50,4))*(9/46) = 3,462%.
Com cartas iniciais de naipes diferentes:
Flush após o flop: 0%
Flush após a virada: 2*combin(12,4)/combin(50,4) = 0,430%.
Descarga após o rio: (2*combin(12,3)*39/combin(50,4))*(9/46) = 1,458%.
Aqui estão as probabilidades cumulativas.
Com cartas fechadas do mesmo naipe:
Probabilidade de flush no flop: 0,842%.
Flush por turno: 2,937%.
Descarga por rio: 6.400%.
Com cartas iniciais de naipes diferentes:
Flush no flop: 0,000%
Descarga por turno: 0,430%.
Descarga por rio: 1,888%.
Olá Wizard, antes de mais nada, gostaria de dizer que adoro as respostas precisas e objetivas que você dá. Enfim, se as cartas iniciais no Hold'em são AA e as cartas do flop são KQ9, qual é a probabilidade de completar um full house? Estou tentando resolver isso há um tempão :( e ainda não tenho uma resposta em que confio.
Você poderia completar o full house com um ás e um rei, dama ou 9. Restam 2 ases e 3 de cada um dos seguintes: rei, dama e 9. Portanto, existem 2 * 3 * 3 = 18 combinações possíveis. A única outra maneira seria um par de rei, dama ou 9. Existem 3 * combinações (3, 2) = 9 combinações possíveis. O número total de combinações é 47 * 46 / 2 = 1081. Portanto, a probabilidade é (18 + 9) / 1081 = 2,50%.
Sou fã há muitos anos (mesmo antes de você se interessar por pôquer e apostas esportivas) e sempre aguardava ansiosamente cada coluna "Pergunte ao Mago". É ótimo ver que você voltou a escrevê-las! Minha pergunta é a seguinte: no meu cassino local, eles oferecem a promoção "Ases Quebrados, Ganhe um Rack" em determinados horários. Ou seja, se você tiver um par de ases em uma das mesas de Texas Hold'em 3-6 ou 4-8 e perder o pote, o cassino lhe dará um rack de fichas (US$ 100). Estou tentando descobrir com que frequência a) eu consigo um par de ases, b) com que frequência eu perderia se jogasse agressivamente como deveria e c) se não seria melhor simplesmente dar check até o final e torcer para perder, já que US$ 100 geralmente é melhor do que o pote valeria de qualquer forma. Qualquer estatística que você tiver seria maravilhosa e sempre bem-vinda! Obrigado novamente e continue esclarecendo as massas!
Obrigado pelas gentis palavras. A probabilidade de você receber um par de ases em uma mão é de 6/1326, ou uma vez a cada 221 mãos. De acordo com a minha seção sobre Texas Hold'em para 10 jogadores (/games/texas-hold-em/10players.html), a probabilidade de ganhar com um par de ases é de 31,36%, assumindo que todos os jogadores permaneçam na partida até o final. No entanto, isso é uma grande incógnita. Se eu tivesse que dar um palpite, estimaria que a probabilidade de ganhar com ases em um jogo real de 10 jogadores seja de cerca de 70%. Portanto, a probabilidade de receber um par de ases e perder é de 0,3 * (1/221) = 0,1357%. Assim, a US$ 100 por ocorrência, isso equivale a 13,57 centavos por mão. Para dez pessoas, isso custa à sala de pôquer US$ 1,36 por mão em média, o que reduz bastante o rake. Eu tendo a concordar com sua estratégia de pagar, o que manterá mais jogadores na mão e aumentará sua chance de perder.
Primeiramente, gostaria de agradecer pelo excelente site. Agora, minha pergunta é a seguinte: estamos jogando Texas Hold'em e acertamos um flush draw no flop com duas cartas baixas. Todos sabemos a porcentagem de acertar o flush, mas o que realmente queremos saber é a porcentagem de ganhar a mão. Digamos que temos certeza de que alguém tem uma carta maior daquele naipe do que a nossa. Então, minha pergunta é: qual a porcentagem de aparecer apenas uma carta daquele naipe e não duas? Atenciosamente.
De nada. Então você tem quatro cartas para um flush com duas cartas na mesa após o flop. A probabilidade de conseguir exatamente uma carta do naipe necessário é 9*38/ combin (47,2) = 342/1081 = 31,64%.
No Texas Hold'em, gostaria de saber a probabilidade de outro jogador ter recebido duas cartas do mesmo naipe para formar um flush maior que o meu, quando há exatamente 3 cartas comunitárias do mesmo naipe no river. Por exemplo, se eu tenho 89 de espadas e as cartas comunitárias incluem o 3, o 7 e o K de espadas, e há 4 espadas maiores que o meu 9 no baralho (TJQA), qual a probabilidade de alguém ter recebido uma mão com duas espadas, incluindo pelo menos uma das espadas maiores (considerando um jogo com 9 jogadores)? E se houver apenas 2 (ou 3 ou x) espadas maiores que a minha maior carta fechada? Obrigado pela ajuda e pelo excelente site.
A tabela a seguir mostra a probabilidade para 1 a 8 jogadores de nível superior e 2 a 10 jogadores, incluindo você. No caso do seu exemplo com 4 jogadores de nível superior e 9 jogadores no total, a probabilidade é de 16,45%. O método que utilizei para calcular essas probabilidades pressupôs independência entre as mãos, o que não é uma suposição correta, mas os resultados devem ser uma estimativa aproximada.
Probabilidade de Flush Mais AltoClassificação (de cima para baixo) por Total de Jogadores (horizontal)Estimativa do Wizard
| Cargos superiores | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0,71% | 1,41% | 2,11% | 2,80% | 3,49% | 4,17% | 4,85% | 5,52% | 6,19% |
| 2 | 1,31% | 2,61% | 3,89% | 5,15% | 6,40% | 7,62% | 8,84% | 10,03% | 11,22% |
| 3 | 1,82% | 3,60% | 5,36% | 7,08% | 8,77% | 10,43% | 12,05% | 13,65% | 15,22% |
| 4 | 2,22% | 4,40% | 6,52% | 8,60% | 10,63% | 12,61% | 14,56% | 16,45% | 18,31% |
| 5 | 2,53% | 4,99% | 7,39% | 9,72% | 12,00% | 14,23% | 16,39% | 18,50% | 20,56% |
| 6 | 2,73% | 5,38% | 7,96% | 10,47% | 12,91% | 15,29% | 17,60% | 19,85% | 22,03% |
| 7 | 2,83% | 5,58% | 8,25% | 10,84% | 13,36% | 15,81% | 18,20% | 20,51% | 22,76% |
| 8 | 2,83% | 5,58% | 8,25% | 10,84% | 13,36% | 15,81% | 18,20% | 20,51% | 22,76% |
Probabilidade de Flush Mais AltoClassificação (de cima para baixo) por Total de Jogadores (horizontal)Simulação de Miplet
| Cargos superiores | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0,69% | 1,41% | 2,12% | 2,83% | 3,54% | 4,25% | 4,96% | 5,66% | 6,36% |
| 2 | 1,28% | 2,60% | 3,91% | 5,21% | 6,48% | 7,77% | 9,05% | 10,31% | 11,56% |
| 3 | 1,79% | 3,61% | 5,41% | 7,19% | 8,92% | 10,68% | 12,41% | 14,11% | 15,79% |
| 4 | 2,19% | 4,40% | 6,58% | 8,75% | 10,85% | 12,94% | 15,01% | 17,04% | 19,04% |
| 5 | 2,50% | 5,00% | 7,47% | 9,92% | 12,28% | 14,63% | 16,94% | 19,21% | 21,43% |
| 6 | 2,71% | 5,40% | 8,06% | 10,69% | 13,23% | 15,74% | 18,23% | 20,65% | 23,03% |
| 7 | 2,81% | 5,61% | 8,36% | 11,08% | 13,70% | 16,30% | 18,86% | 21,37% | 23,82% |
| 8 | 2,81% | 5,61% | 8,36% | 11,08% | 13,70% | 16,30% | 18,86% | 21,37% | 23,82% |
Ótimo site. Estou perguntando isso para meu próprio conhecimento. Eu estava jogando uma partida de Texas Hold'em com 4 pessoas. Recebi um par de ases. Consegui um Royal Flush no river. Gostaria de saber quais são as chances de fazer um Royal Flush no river com um par de ases como mão inicial?
Obrigado. Supondo que o royal flush seja composto por um dos seus dois ases, o número de maneiras de formar um royal flush no river é 2 * 46 = 92. Isso inclui os dois naipes dos seus ases na mão e as 46 possibilidades para a carta extra. Existem combin (50, 5) = 2.118.760 maneiras de distribuir 5 cartas dentre 50. Portanto, a probabilidade é 92/2.118.760 = 1 em 23.030.
Se o flop mostrar uma trinca do mesmo naipe e eu não tiver nenhuma carta que combine com o naipe do flop, e restarem dez jogadores na mesa, qual é a probabilidade de alguém ter um flush?
A probabilidade de qualquer jogador ter um flush é combin (11,2)/combin(49,2) = 55/1176 = 4,68%. Assumindo independência entre as mãos, o que não é o caso, a probabilidade de 9 jogadores não terem um flush é (1 − 0,0468%) 9 = 64,98%. Portanto, a probabilidade de pelo menos um jogador ter um flush é 1 - 0,6498 = 35,02%. Esta é apenas uma estimativa rápida. Se eu fizesse uma simulação aleatória, acho que a probabilidade seria um pouco maior, devido à dependência entre as mãos.
Prezado Sr. Mago, recentemente tenho tentado calcular a probabilidade de formar um flush no Texas Hold'em com duas cartas do mesmo naipe. Meu resultado tem sido de 5,8%, mas isso me parece incorreto. Sua ajuda seria muito apreciada. Obrigado.
A probabilidade de formar um flush, com exatamente três cartas do mesmo naipe das suas cartas iniciais, é combin (11,3)×combin(39,2)/combin(50,5) = 122265/2598960 = 0,057706. A probabilidade de formar um flush, com mais quatro cartas do mesmo naipe das suas cartas iniciais, é combin(11,4)×combin(39,1)/combin(50,5) = 2145/2118760 = 0,001012. A probabilidade de formar um flush, com mais cinco cartas do mesmo naipe das suas cartas iniciais, é combin(11,5)/combin(50,5) = 462/2118760 = 0,000218. A probabilidade de fazer um flush na mesa em outro naipe é 3×combin(13,5)/combin(50,5) = 3861/2118760 = 0,001822. Somando tudo isso, você obtém 0,057706 + 0,001012 + 0,000218 + 0,001822 = 0,060759.
Qual a probabilidade de se ver um "board quebrado" no Texas Hold'em? Ou seja, cinco cartas na mesa onde não existe nenhum par, nenhum flush possível e nenhuma sequência possível.
O número de combinações de cinco classificações diferentes no tabuleiro é combin (13,5)*4 5 = 1287 × 1024 = 1.317.888.
A probabilidade de que esses cinco valores representem três naipes, dois de dois e um de um, é combin(4,2)*2*combin(5,2)*combin(3,2)=360. Combin(4,2) é o número de maneiras de escolher dois naipes dentre os quatro possíveis para os naipes representados duas vezes. 2 representa as duas maneiras de escolher o naipe representado uma vez. Combin(5,2) é o número de maneiras de escolher dois valores dentre os cinco possíveis para o primeiro naipe de duas cartas. 4 5 é o número de maneiras de escolher dois valores dentre os três possíveis para o outro naipe de duas cartas.
A probabilidade de que esses cinco valores representem quatro naipes, um de dois e três de um, é 4*combin(5,2)*3*2=240. 4 é o número de maneiras de escolher um naipe dentre os quatro para os naipes representados duas vezes. Combin(5,2) é o número de maneiras de escolher dois valores dentre os cinco para esse naipe de duas cartas. 3 é o número de maneiras de escolher um valor dentre os três restantes para o primeiro naipe de um. 2 é o número de maneiras de escolher um valor dentre os dois para o segundo naipe de um.
Existem 4⁵ = 1024 maneiras de organizar quatro naipes em cinco fileiras diferentes.
Portanto, a probabilidade de haver no máximo duas cartas do mesmo naipe é (360+240)/1024 = 600/1024 = 58,59%.
Existem combin(13,5)=1287 maneiras de organizar 5 posições dentre 13. O número dessas combinações em que não há três posições dentro de um intervalo de 5 é 79. Não existe uma fórmula simples para isso. Tive que testar todas as combinações. Portanto, a probabilidade de as posições estarem suficientemente espaçadas é 79/1287 = 6,14%.
Portanto, a probabilidade de uma tábua quebrada é (1317888/2596960)*(600/1024)*(79/1287) = 1,825211%.
Fui desafiado quanto ao número de sequências quebradas que consegui. Aqui está uma lista com todas as 79 possíveis.
| 2378Q 2378 mil 2379Q 2379 mil 237TQ 237TK 237JQ 237JK 237QK 2389 mil 238TK 238JK 238QK 2479Q 2479 mil 247TQ 247TK 247JQ 247JK 247QK | 2489 mil 248TK 248JK 248QK 257TQ 257TK 257JQ 257JK 257QK 258TK 258JK 258QK 267JQ 267JK 267JA 267QK 267QA 267KA 268JK 268JA | 268QK 268QA 268KA 269JA 269QA 269KA 278QK 278QA 278KA 279QA 279KA 289KA 3489 mil 348TK 348JK 348QK 358TK 358JK 358QK 368JK | 368JA 368QK 368QA 368KA 369JA 369QA 369KA 378QK 378QA 378KA 379QA 379KA 389KA 469JA 469QA 469KA 479QA 479KA 489KA |
Jogo Texas Hold'em no Caesars Indiana. Eles têm um Jackpot de Bad Beat, que agora consiste em perder uma quadra ou melhor. Ambos os jogadores precisam jogar suas duas cartas fechadas, e é necessário que quatro jogadores recebam cartas. Minha pergunta é: qual a probabilidade de qualquer mão ser uma mão de Bad Beat, supondo que todos os jogadores permaneçam até o final?
Na minha nova seção "Bad Beat Jackpot", mostro que a probabilidade desse tipo de azar em um jogo com 10 jogadores é de 0,0000108, ou cerca de 1 em 93.000.
Na sua tabela de retorno do Ultimate Texas Hold 'Em , por que um aumento grande é recomendado para mãos de duas cartas listadas na tabela que têm um retorno esperado negativo? Por exemplo, K/2 do mesmo naipe.
De acordo com minhas probabilidades para Texas Hold 'Em de dois jogadores , os seguintes são os resultados possíveis com K/2 do mesmo naipe:
Vitória de 51,24%
Perda de 44,82%
Empate de 3,94%
Minha tabela no Ultimate Texas Hold 'Em mostra que o jogador tem vantagem na aposta Play, mas desvantagem nas apostas Ante e Blind. Nesse caso, o jogador está com odds desfavoráveis no Ante e no Blind. No entanto, suas odds são favoráveis na aposta Play. Portanto, ao fazer o aumento máximo, ele está obtendo o máximo valor de sua chance de ganhar, que é superior a 50%. As odds desfavoráveis nas outras duas apostas reduzem o valor total para menos de 50%. Esse valor seria ainda menor com um aumento menor.
Na World Series of Poker de 2008, Motoyuki Mabuchi perdeu para o Royal Flush de Justin Phillips por causa de uma quadra de ases. Tenho uma pergunta simples sobre a probabilidade disso acontecer. A ESPN e outros veículos citaram uma probabilidade de aproximadamente 1 em 2,7 bilhões. Parece-me que eles simplesmente pegaram a probabilidade publicada de uma quadra e multiplicaram pela probabilidade de um Royal Flush. Esse é o método de cálculo correto?
Discordo também da probabilidade de 1 em 2,7 bilhões. Como você disse, eles parecem ter calculado as probabilidades independentemente para cada jogador, considerando apenas o caso em que ambos usam as duas cartas fechadas, e multiplicado os resultados. Usando esse método, chego a uma probabilidade de 0,000000000341101, ou cerca de 1 em 2,9 bilhões. Talvez a probabilidade de 1 em 2,7 bilhões também envolva um erro de arredondamento acumulado nas probabilidades de ambos os jogadores. Além disso, eles aparentemente se esqueceram de multiplicar a probabilidade por 2, por motivos que explicarei mais adiante.
Existem três maneiras pelas quais uma quadra de ases pode perder para um royal flush, como segue.
Caso 1: Um jogador tem duas cartas para um royal flush, o outro tem dois ases, e a mesa contém os outros dois ases, as outras duas cartas para o royal flush e qualquer outra carta.
Exemplo:
Jogador 1:

Jogador 2:

Quadro: 




Na maioria das salas de poker, para se qualificar para um jackpot de bad beat, tanto o jogador vencedor quanto o perdedor devem usar as duas cartas fechadas. Esse foi também o tipo de bad beat mostrado no vídeo; na verdade, essas eram exatamente as cartas.
Caso 2: Um jogador tem duas cartas para um royal flush (TK), o outro tem um ás e uma carta "em branco", e a mesa contém os outros três ases e as duas cartas restantes para o royal flush.
Exemplo:
Jogador 1:

Jogador 2:

Quadro: 




Caso 3: Um jogador tem uma carta para um royal flush (TK) e uma carta em branco, o outro tem dois ases, e a mesa contém os outros dois ases e as três cartas restantes para o royal flush.
Exemplo:
Jogador 1:

Jogador 2:

Quadro: 




A tabela a seguir mostra o número de combinações para cada caso, tanto para os jogadores quanto para o tabuleiro. A célula inferior direita mostra que o número total de combinações é 16.896.
Combinações de Bad Beat
| Caso | Jogador 1 | Jogador 2 | Quadro | Produto |
|---|---|---|---|---|
| 1 | 24 | 3 | 44 | 3.168 |
| 2 | 24 | 132 | 1 | 3.168 |
| 3 | 704 | 3 | 1 | 2.112 |
| Total | 8.448 |
No entanto, mesmo que trocássemos as cartas dos dois jogadores, ainda teríamos uma bad beat. Portanto, devemos multiplicar o número de combinações por 2. Ajustando para isso, o total de combinações válidas é 2 × 8.448 = 16.896.
O número total de todas as combinações possíveis no Texas Hold'em para dois jogadores é combin (52,2) × combin(50,2) × combin(48,5) = 2.781.381.002.400. Portanto, a probabilidade de uma quadra de ases perder para um royal flush é 8.448/2.781.381.002.400 = 0,0000000060747, ou cerca de 1 em 165 milhões. A probabilidade de apenas uma bad beat (caso 1) é de 1 em 439 milhões. A simples razão pela qual as probabilidades não são tão desfavoráveis quanto relatado naquele vídeo é que as duas mãos se sobrepõem, com o ás em comum. Em outras palavras, os dois eventos estão positivamente correlacionados.
Você está absolutamente certo, de acordo com o artigo " Dizendo a Verdade sobre o Video Poker de Nova York" . O resultado para o jogador é de fato predeterminado. Independentemente das cartas que o jogador mantiver, ele não pode evitar seu destino. Se o jogador tentar deliberadamente evitar seu destino, o jogo utilizará um recurso de "anjo da guarda" para corrigir o erro. Concordo plenamente com o autor que tais jogos deveriam alertar o jogador de que não se trata de um video poker real e que a tabela de pagamentos não representa as probabilidades reais do jogador. Vale ressaltar também que esse tipo de máquina de video poker fraudulenta não se restringe a Nova York.
Olá, sou um aluno do sétimo ano do Havaí. Estou fazendo um projeto para a feira de ciências sobre pôquer e embaralhamento. Estou usando seus gráficos sobre a porcentagem de vitórias de mãos de Texas Hold'em com um par de cartas, de acordo com o número de jogadores na partida. Gostaria que você pudesse responder a algumas perguntas que me ajudariam com o meu projeto:
- Como você chegou às porcentagens apresentadas nos gráficos?
- Se você utilizou um programa de computador, como o desenvolveu e quanto tempo levou?
- Você afirmou que começou o Wizard of Odds como um hobby. Os experimentos mudaram à medida que seu site se tornou mais conhecido? Por que sim ou por que não?
- A tabela para dois jogadores foi gerada por um programa de busca exaustiva, que percorreu todas as 1225 cartas possíveis dos oponentes e as 1712304 cartas possíveis das comunidades. Para três a oito jogadores, a busca exaustiva levaria um tempo proibitivo, então fiz uma simulação aleatória.
- Eu escrevo quase todos os meus programas em C++, incluindo os dois que acabei de mencionar. O restante é em Java ou Perl. Na maior parte, copiei e colei código de outros programas de pôquer. O novo código levou apenas cerca de um dia para ser escrito.
- Sim, comecei meu site como um hobby em junho de 1997. Só em janeiro de 2000 aceitei anúncios e tentei transformá-lo em um negócio. Ele passou por três domínios diferentes ao longo dos anos. Veja como era em maio de 1999. O objetivo do site sempre foi o mesmo: ser um recurso para estratégias de apostas baseadas em matemática. Ao longo dos anos, fui adicionando mais jogos e conteúdo. Uma experiência foi fornecer meus palpites da NFL para a temporada de 2005 , o que foi um fracasso total.
Olá, Wizard. Li suas perguntas sobre Texas Hold 'Em e notei que você calculou uma probabilidade de 59,85% de ver um ás ou um rei na mesa, mesmo com um par de damas. Como você chegou a esse número?
Existem combin (50,5) = 2.118.760 combinações de cinco cartas dentre as 50 restantes no baralho. Dessas, 42 são do 2 à Q. O número de combinações de 5 cartas dentre as 42 é combin(42,5) = 850.668. Portanto, a probabilidade de não obter um rei ou um ás é 850.668/2.118.760 = 40,15%. Assim, a probabilidade de obter pelo menos um ás ou um rei é 1 - 40,15% = 59,85%.
Um cálculo alternativo é 1 - pr(primeira carta no flop não é ás ou rei) × pr(segunda carta no flop não é ás ou rei) × pr(terceira carta no flop não é ás ou rei) × pr(quarta carta no flop não é ás ou rei) × pr(quinta carta no flop não é ás ou rei) = 1 - (42/50) × (41/49) × (40/48) × (39/47) × (38/46) = 59,85%.
Em uma partida de Texas Hold'em, qual a probabilidade de eu receber exatamente mais duas cartas do mesmo naipe no flop?
Existem combin (11,2) = 55 maneiras de obter mais duas cartas do mesmo naipe e 39 maneiras de obter uma carta de naipe diferente. Existem combin(50,3) = 19.600 combinações possíveis de cartas no flop. Portanto, a probabilidade de ter exatamente quatro cartas para um flush após o flop é 55 × 39 / 19.600 = 10,94%.
Eu estava envolvido em uma partida de pôquer online e gostaria de saber as probabilidades disso acontecer, por favor:
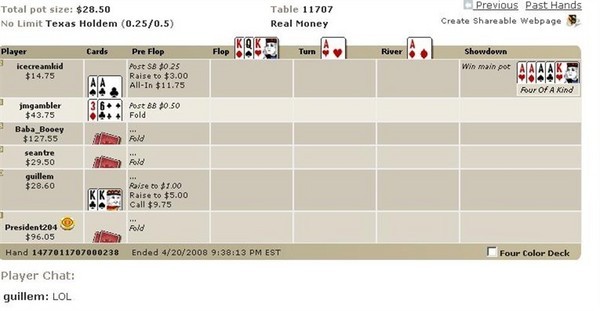
Normalmente, estou farto de perguntas sobre bad beats, mas esta foi dolorosa demais para ignorar. Antes da primeira carta ser distribuída, a probabilidade de uma quadra de reis ser derrotada por uma quadra de ases, em um jogo de dois jogadores, com ambos os jogadores tendo pares na mão, é 2 * combin (4,2) * combin(4,2) * 44 / (combin(52,2) * combin(50,2) * combin(48,5)) = 2 * 6 * 6 * 44 / (1326 * 1225 * 1712304) = 1 em 877.961.175. Este era um jogo de seis jogadores, então existem combin(6,2) = 15 pares de jogadores diferentes. Em um jogo de seis jogadores, a probabilidade é 15 vezes maior, ou 1 em 58.530.745. Após a distribuição das cartas iniciais indicadas e antes do flop, a probabilidade de a mão terminar como terminou é de 1 em 38.916.
Um cassino em Las Vegas está anunciando uma promoção: faça um flush com as quatro cartas do mesmo naipe e ganhe US$ 400. Você precisa usar as duas cartas da sua mão e o jogo tem um limite de tempo de cinco horas. Considerando 35 mãos por hora e que o cronômetro começa a contar a partir do primeiro flush, qual é a probabilidade de conseguir os outros três flushes dentro de cinco horas? Obrigado.
Vamos supor que seu primeiro flush seja de espadas. Com 35 mãos por hora, em cinco horas você poderia jogar 175 mãos. Você teria então 175 mãos para formar um flush de copas, ouros e paus. Vou assumir que o jogador nunca desiste de uma mão que tenha a possibilidade de formar um flush em um dos naipes que ele precisa.
A probabilidade de um flush de um naipe específico, digamos copas, usando ambas as cartas fechadas é combin(13,2)×[combin(11,3)×combin(39,2) + combin(11,4)×39 + combin(11,5)]/(combin(52,2)×combin(50,5)) = 10576566/2809475760=0,003764605. Nas próximas 175 mãos, a probabilidade de não conseguir um flush de copas seria (1-0,003764605) 175 =0,51682599.
Seria incorreto dizer que a probabilidade de não formar os outros três naipes seria pr(sem flush de copas) + pr(sem flush de ouros) + pr(sem flush de paus), porque você estaria contabilizando duas vezes a probabilidade de não formar dois deles. Portanto, você deveria adicionar pr(sem flush de copas ou ouros) + pr(sem flush de copas ou paus) + pr(sem flush de paus ou ouros). No entanto, isso subtrairia incorretamente a probabilidade de não formar os três flushes. Então, você deveria adicionar pr(sem flush de paus, ouros ou copas).
A probabilidade de jogar 175 mãos e nunca conseguir nenhum dos dois naipes específicos é (1-2×0,003764605) 175 =0,266442448.
A probabilidade de jogar 175 mãos e nunca conseguir nenhum dos três naipes restantes é (1-3×0,003764605) 175 =0,137015266.
Portanto, a resposta é 1-3×0,51682599 + 3×0,266442448 - 0,137015266 = 0,111834108.
Gostaria de agradecer a dwheatley pela ajuda com este problema. Ele foi discutido no meu fórum no Wizard of Vegas .
Doyle Brunson é famoso por ter vencido o Evento Principal da World Series of Poker em 1976 e 1977. Em ambas as ocasiões, ele tinha 10-2 como cartas iniciais e, nas duas vezes, fez um full house no river. Qual a probabilidade disso?
Dadas duas cartas de valores diferentes, a probabilidade de formar um full house é de 1 em 121,6. A probabilidade de formar um full house no river é de 1 em 207.
A probabilidade de formar uma mão dessas no river duas vezes em duas tentativas é de 1 em 43.006.
A probabilidade de isso acontecer com as mesmas duas cartas iniciais, considerando apenas a classificação, é de 1 em 3.564.161.
A probabilidade de isso acontecer exatamente com 10-2 nas duas vezes é de 1 em 295.379.826.
Acabei de voltar da noite de pôquer no VFW. Fiz 6-6 três vezes seguidas! Nunca tinha acontecido isso antes. Qual a probabilidade de conseguir um par de cartas do mesmo valor três vezes seguidas em uma noite? Considere que uma noite tem um total de 120 rodadas.
A resposta e a solução aparecem na seguinte tag de spoiler.
Existem quatro estados possíveis em que você pode se encontrar a qualquer momento:
- Estado 1: A primeira mão ou qualquer mão em que a última mão não tenha sido um par na mão.
- Estado 2: A última mão era um par na mão.
- Estado 3: As duas últimas mãos eram o mesmo par de cartas.
- Estado 4: Já foi alcançada a combinação de três pares de cartas iguais em sequência.
Se você estiver no estado 1, poderá avançar para o estado 2 com uma probabilidade de 3/51. Caso contrário, você permanece no estado 1.
Se você estiver no estado 2, você pode avançar para o estado 3 com uma probabilidade de (4/52)×(3/51). Caso contrário, você volta para o estado 1.
Se você estiver no estado 3, você pode avançar para o estado 4 com uma probabilidade de (4/52)×(3/51). Caso contrário, você volta para o estado 1.
Se você estiver no estado 4, você permanece lá.
Dito isso, você pode criar sua matriz de transição, T, da seguinte forma:
| 0,941176 | 0,058824 | 0,000000 | 0,000000 |
| 0,941176 | 0,054299 | 0,004525 | 0,000000 |
| 0,941176 | 0,054299 | 0,000000 | 0,004525 |
| 0,000000 | 0,000000 | 0,000000 | 1.000000 |
Foram jogadas 120 mãos no total, então encontre T^120.
| 0,941044 | 0,058549 | 0,000265 | 0,000141 |
| 0,941025 | 0,058548 | 0,000265 | 0,000162 |
| 0,936786 | 0,058284 | 0,000264 | 0,004666 |
| 0,000000 | 0,000000 | 0,000000 | 1.000000 |
A célula superior direita mostra a probabilidade de que, começando no estado 1, chegaremos ao estado 4 após 120 mãos iniciais em uma sequência de três mãos, que é de 0,000141471.
Tomando o inverso desse número, a probabilidade é de 1 em 7068,605131.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
No filme Casino Royale, na mão final de um torneio de pôquer, os quatro jogadores têm as seguintes mãos:
- Descarga
- Casa cheia
- Casa cheia (de valor diferente da primeira)
- Straight flush
Qual é a probabilidade disso?
Para isso, precisei fazer uma simulação. Na minha simulação, assumi que ninguém jamais desiste. Em quase 2,2 bilhões de rodadas, isso aconteceu 312 vezes. Isso equivale a uma probabilidade de cerca de 1 em sete milhões.


