Nesta página
Probabilidade dos dados
Nesta página
Introdução
Antes de jogar qualquer jogo de dados, é bom saber a probabilidade de se obter um determinado total. Primeiro, vamos analisar as possibilidades do total de dois dados. A tabela abaixo mostra as seis possibilidades para o dado 1 na coluna da esquerda e as seis possibilidades para o dado 2 na coluna superior. O corpo da tabela mostra a soma dos dados 1 e 2.
Totais de dois dados
| Morra 1 | Morra 2 | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
As cores do corpo da tabela ilustram o número de maneiras de se obter cada total. A probabilidade de se obter um determinado total é o número de maneiras de se obter esse total dividido pelo número total de combinações (36). Na tabela a seguir, são mostrados o número específico de maneiras de se obter cada total e a probabilidade de se obter esse total.
| Total | Número de Combinações | Probabilidade |
|---|---|---|
| 2 | 1 | 2,78% |
| 3 | 2 | 5,56% |
| 4 | 3 | 8,33% |
| 5 | 4 | 11,11% |
| 6 | 5 | 13,89% |
| 7 | 6 | 16,67% |
| 8 | 5 | 13,89% |
| 9 | 4 | 11,11% |
| 10 | 3 | 8,33% |
| 11 | 2 | 5,56% |
| 12 | 1 | 2,78% |
| Total | 36 | 100% |
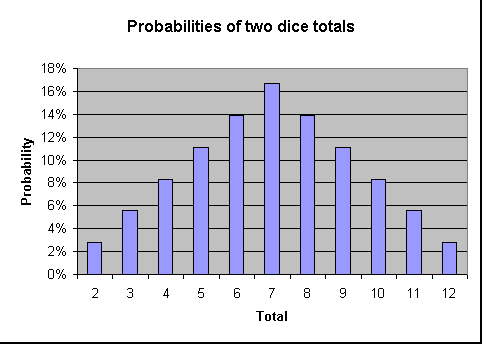
A tabela a seguir mostra a probabilidade de obter cada total. Como a tabela demonstra, quanto mais próximo de 7 for o total, maior será a probabilidade de obtê-lo.
Bônus de cassino online Dados Ver tudo
Exemplo de aposta no campo
Agora que entendemos a probabilidade de obter cada total, podemos aplicar essa informação aos jogos de dados nos cassinos para calcular a vantagem da casa. Por exemplo, considere a aposta no campo no craps . Essa aposta paga 1:1 (pagamento igual) se o próximo lançamento for 3, 4, 9, 10 ou 11, 2:1 (o dobro da aposta) no 2 e 3:1 (o triplo da aposta) no 12. Observe que existem 7 totais vencedores e apenas 4 perdedores, o que pode levar alguém desavisado a pensar que é uma boa aposta.
O retorno do jogador pode ser definido como a soma dos produtos da probabilidade de cada evento e do retorno líquido desse evento. A tabela a seguir mostra cada total possível, o retorno líquido, a probabilidade de obter esse total e o retorno médio. O retorno médio é o produto do retorno líquido pela probabilidade. O retorno do jogador é a soma dos retornos médios.
| Total | Retorno líquido | Probabilidade | Retorno médio |
|---|---|---|---|
| 2 | 2 | 0,0278 | 0,0556 |
| 3 | 1 | 0,0556 | 0,0556 |
| 4 | 1 | 0,0833 | 0,0833 |
| 5 | -1 | 0,1111 | -0,1111 |
| 6 | -1 | 0,1389 | -0,1389 |
| 7 | -1 | 0,1667 | -0,1667 |
| 8 | -1 | 0,1389 | -0,1389 |
| 9 | 1 | 0,1111 | 0,1111 |
| 10 | 1 | 0,0833 | 0,0833 |
| 11 | 1 | 0,0556 | 0,0556 |
| 12 | 3 | 0,0278 | 0,0834 |
| Total | 1 | -0,0278 |
A última linha mostra que o retorno do jogador é de -0,0278, ou seja, para cada US$ 1 apostado, o jogador pode esperar perder 2,78 centavos. A perda do jogador é o ganho da casa, portanto, a vantagem da casa é o produto de -1 pelo retorno do jogador, neste caso 0,0278 ou 2,78%.
Para as probabilidades na soma de mais de dois dados, consulte a minha seção sobre probabilidades para 1 a 25 dados .
Ohio Cassinos online recomendados
Ver tudo
BÔNUS DE ATÉ $11.000
Jogadores de todos os EUA são bem-vindos.
Mais de 200 jogos de cassino
Jogue no PC ou no celular
BÔNUS DE ATÉ $3000
Cassino e apostas esportivas
Apenas jogadores americanos
Jogue no computador ou no celular.
BÔNUS DE ATÉ 777$
Grande bônus de boas-vindas
Torneios diários de cassino
Jogos populares
$7777 + 300 Giros Grátis
Jogos com crupiê ao vivo
Torneios diários gratuitos
Compatível com dispositivos móveis e computadores.