Nesta página
Sistema de apostas Labouchere
Introdução
O Labouchere (também conhecido como Martingale de Cancelamento e Martingale Dividido) é um sistema de apostas bastante conhecido. Geralmente é utilizado em jogos com odds de 1 para 1. Consiste em escrever uma lista de números e, em seguida, riscar dois após uma vitória e adicionar um após uma derrota. Como a maioria dos sistemas de apostas, geralmente resulta em lucro na sessão, mas também em grandes perdas quando não resulta.
A lógica por trás do Labouchere é que o jogador precisa ganhar apenas 1/3 das vezes (e não ficar sem dinheiro) para que o sistema funcione. Alguns podem argumentar que a Lei dos Grandes Números afirma que quanto mais apostas forem feitas, mais a proporção entre vitórias e apostas se aproximará da proporção esperada. Embora isso seja verdade, uma sequência de derrotas pode fazer com que as apostas aumentem rapidamente, às vezes esgotando a banca do jogador.
Regras
- O jogador definirá seu objetivo de vitória e sua banca.
- O jogador dividirá o resultado do seu gol da vitória por 10.
- O jogador escreverá o quociente da etapa 2 dez vezes, na horizontal.
- O jogador apostará a soma dos números da esquerda e da direita na lista em uma aposta com probabilidades iguais*.
- Se o jogador ganhar a aposta na etapa 4, ele riscará os números da esquerda e da direita na lista.
- Se o jogador perder a aposta na etapa 4, ele adicionará um novo elemento à extremidade direita da lista, contendo o valor perdido.
- Volte ao passo 4, a menos que todos os elementos da lista tenham sido riscados (sucesso) ou que o saldo do jogador esteja esgotado (fracasso).
*: Exceções
- Se houver apenas um elemento na lista, aposte nele.
- Se o saldo do jogador for maior que zero, mas não suficiente para cobrir a soma dos elementos da esquerda e da direita na lista, aposte o saldo restante. Se essa aposta for vencedora e o valor apostado for menor que o elemento da extremidade direita da lista, subtraia o valor apostado do elemento da direita. Se essa aposta for vencedora e o valor for maior que o elemento da extremidade direita da lista, risque o elemento da direita e deduza o valor apostado menos o elemento da direita do elemento da esquerda.
Exemplo
- Neste exemplo, o objetivo do jogador é ganhar 50 dólares e sua banca é de 1.000 dólares. Ele começa dividindo 50 dólares por 10 e escrevendo o quociente dez vezes: 5-5-5-5-5-5-5-5-5-5.
- A primeira aposta do jogador é de $10 ($5 + $5), que ele ganha, e marca os elementos da direita e da esquerda: 5-5-5-5-5-5-5-5.
- A segunda aposta do jogador é de $10 ($5 + $5), que ele ganha, e risca os elementos da direita e da esquerda: 5-5-5-5-5-5.
- A terceira aposta do jogador é de $10 ($5 + $5), que ele ganha, e risca os elementos da direita e da esquerda: 5-5-5-5.
- A quarta aposta do jogador é de $10 ($5 + $5), que ele perde, e adiciona à extremidade direita da lista, ficando: 5-5-5-5-10.
- A quinta aposta do jogador é de $15 ($5 + $10), que ele perde, e adiciona ao final direito da lista, ficando: 5-5-5-5-10-15.
- A sexta aposta do jogador é de $20 ($5 + $15), que ele ganha, e risca os elementos da direita e da esquerda: 5-5-5-10.
- A sétima aposta do jogador é de $15 ($5 + $10), que ele perde, e adiciona à extremidade direita da lista, ficando: 5-5-5-10-15.
- A oitava aposta do jogador é de $20 ($5 + $15), que ele perde, e adiciona ao final direito da lista, ficando: 5-5-5-10-15-20.
- A nona aposta do jogador é de $25 ($5 + $20), que ele perde, e adiciona ao final direito da lista, ficando: 5-5-5-10-15-20-25.
- A décima aposta do jogador é de $30 ($5 + $25), que ele ganha, e risca os elementos da direita e da esquerda: 5-5-10-15-20.
- A 11ª aposta do jogador é de $25 ($5 + $20), que ele ganha, e risca os elementos da direita e da esquerda: 5-10-15.
- A 12ª aposta do jogador é de $20 ($5 + $15), que ele perde, e adiciona ao final direito da lista, ficando: 5-10-15-20.
- A 13ª aposta do jogador é de $25 ($5 + $20), que ele perde, e adiciona ao final direito da lista, ficando: 5-10-15-20-25.
- A 14ª aposta do jogador é de $30 ($5 + $25), que ele ganha, eliminando os elementos da esquerda e da direita, restando: 10-15-20.
- A 15ª aposta do jogador é de $30 ($10 + $20), que ele ganha, eliminando os elementos da esquerda e da direita, restando: 15.
- A 16ª aposta do jogador é de $15 (o único elemento restante), que ele perde, adicionando ao lado direito da lista: 15-15.
- A 17ª aposta do jogador é de $30 ($15+$15), que ele perde, adicionando ao final direito da lista: 15-15-30.
- A 18ª aposta do jogador é de $45 ($15 + $30), que ele perde, adicionando ao final direito da lista: 15-15-30-45.
- A 19ª aposta do jogador é de $60 ($15 + $45), que ele perde, adicionando ao final direito da lista: 15-15-30-45-60.
- A 20ª aposta do jogador é de $75 ($15 + $60), que ele ganha, eliminando os elementos da esquerda e da direita, restando: 15-30-45.
- A 21ª aposta do jogador é de $60 ($15 + $45), que ele ganha, eliminando os elementos da esquerda e da direita, restando: 30.
- A 22ª aposta do jogador é de 30 dólares (o único elemento restante), que ele ganha, declarando vitória e saindo com 50 dólares em ganhos.
Resultados da simulação
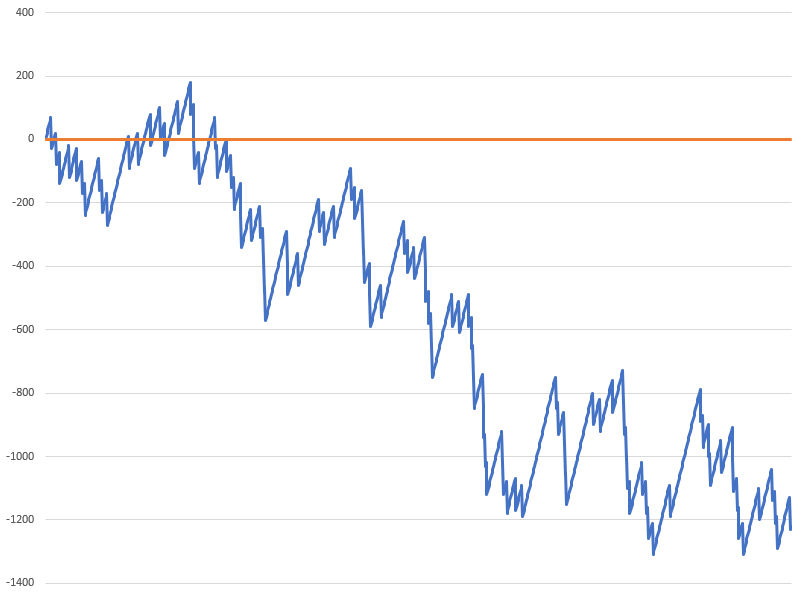
Para demonstrar o que esperar ao usar o Labouchere, elaborei uma simulação que seguiu as regras acima, baseada em diversas apostas e jogos. A simulação utilizou um gerador de números aleatórios Mersenne Twister. Em cada simulação, o objetivo de ganho era de dez unidades. Testei a simulação com as seguintes bancas: 50, 100, 250, 500, 1000 e 2500 unidades.
A primeira simulação baseia-se na aposta no Jogador no bacará . O tamanho da simulação abrange mais de 6 bilhões de sessões. Como lembrete, a vantagem teórica da casa na aposta no Jogador é de 1,235%.
Simulação de Bacará — Aposta do Jogador
| Estatística | 50 unidades | 100 unidades | 250 unidades | 500 unidades | 1000 unidades | 2500 unidades |
|---|---|---|---|---|---|---|
| Probabilidade de gol vencedor alcançado | 81,47% | 89,52% | 95,34% | 97,53% | 98,70% | 99,45% |
| Número médio de apostas | 17.810 | 19.565 | 20,766 | 21.184 | 21.405 | 21.542 |
| Aposta média de unidades | 90,651 | 123,859 | 171,423 | 209.457 | 249.284 | 304,325 |
| Vitórias esperadas por sessão | -1,119 | -1,528 | -2,113 | -2,588 | -3,084 | -3,765 |
| Proporção entre dinheiro perdido e dinheiro apostado | 1,234% | 1,234% | 1,233% | 1,236% | 1,237% | 1,237% |
A próxima simulação é sobre a aposta "pass" no craps . Lembrando que a vantagem da casa na aposta "pass" é de 7/495 = 1,411%. O tamanho da simulação é de 8,7 bilhões de sessões.
Simulação de Craps — Aposta Pass
| Estatística | 50 unidades | 100 unidades | 250 unidades | 500 unidades | 1000 unidades | 2500 unidades |
|---|---|---|---|---|---|---|
| Probabilidade de gol da vitória alcançada | 81,40% | 89,47% | 95,31% | 97,51% | 98,69% | 99,45% |
| Número médio de apostas | 17.821 | 19.583 | 20.791 | 21.213 | 21.435 | 21.573 |
| Aposta total média | 82.123 | 112.285 | 155,551 | 190.203 | 226.522 | 276,844 |
| Vitórias esperadas por sessão | -1,160 | -1,586 | -2,198 | -2,689 | -3.201 | -3,915 |
| Proporção entre dinheiro perdido e dinheiro apostado | 1,413% | 1,413% | 1,413% | 1,414% | 1,413% | 1,414% |
A próxima simulação é baseada na aposta "don't pass" no craps . O tamanho da simulação foi de mais de 6 bilhões de sessões. Lembrando que a vantagem da casa na aposta "don't pass" é de 1,364%.
Simulação de Craps — Não Passe
| Estatística | 50 unidades | 100 unidades | 250 unidades | 500 unidades | 1000 unidades | 2500 unidades |
|---|---|---|---|---|---|---|
| Probabilidade de gol da vitória alcançada | 81,41% | 89,48% | 95,31% | 97,52% | 98,70% | 99,45% |
| Número médio de apostas | 17,819 | 19.579 | 20,786 | 21.206 | 21.427 | 21.566 |
| Aposta total média | 84,447 | 115.440 | 159,904 | 195,465 | 232,766 | 284,361 |
| Vitórias esperadas por sessão | -1,152 | -1,571 | -2,182 | -2,666 | -3,171 | -3,863 |
| Proporção entre dinheiro perdido e dinheiro apostado | 1,364% | 1,361% | 1,365% | 1,364% | 1,362% | 1,358% |
A próxima simulação baseia-se em qualquer aposta com probabilidade igual (par ou ímpar) na roleta com um único zero. O tamanho da simulação foi superior a 6,9 bilhões de sessões. A vantagem teórica da casa na roleta com um único zero é de 1/37 = 2,703%.
Simulação de Roleta — Zero Único
| Estatística | 50 unidades | 100 unidades | 250 unidades | 500 unidades | 1000 unidades | 2500 unidades |
|---|---|---|---|---|---|---|
| Probabilidade de gol da vitória alcançada | 79,52% | 88,01% | 94,41% | 96,93% | 98,33% | 99,26% |
| Número médio de apostas | 18.123 | 20.070 | 21.465 | 21,978 | 22.257 | 22.441 |
| Aposta total média | 84,738 | 117,939 | 167,599 | 209.142 | 254,264 | 319.542 |
| Vitórias esperadas por sessão | -2,291 | -3,188 | -4,527 | -5,652 | -6,877 | -8,648 |
| Proporção entre dinheiro perdido e dinheiro apostado | 2,703% | 2,703% | 2,701% | 2,703% | 2,705% | 2,706% |
A próxima simulação baseia-se em qualquer aposta com probabilidades iguais na roleta de duplo zero. O tamanho da simulação ultrapassou 8 bilhões de sessões.
Simulação de Roleta — Duplo Zero
| Estatística | 50 unidades | 100 unidades | 250 unidades | 500 unidades | 1000 unidades | 2500 unidades |
|---|---|---|---|---|---|---|
| Probabilidade de gol da vitória alcançada | 75,45% | 84,71% | 92,23% | 95,44% | 97,34% | 98,71% |
| Número médio de apostas | 18.697 | 21.046 | 22,881 | 23,615 | 24.046 | 24.351 |
| Aposta total média | 89,839 | 129.507 | 193.860 | 252.141 | 320.010 | 426.256 |
| Vitórias esperadas por sessão | -4,729 | -6,817 | -10,204 | -13,270 | -16,843 | -22,427 |
| Proporção entre dinheiro perdido e dinheiro apostado | 5,263% | 5,264% | 5,264% | 5,263% | 5,263% | 5,261% |
Vídeo
Espero que gostem do meu vídeo explicando o Labouchere e o que vocês podem esperar ao tocá-lo.
Link direto: https://www.youtube.com/watch?v=5FdbVeNX59A