Nesta página
Molly de Três Pontos
Introdução
O Three Point Molly é um sistema de apostas baseado no jogo de dados (craps). Não há uma maneira fácil de implementá-lo em outros jogos. O conceito é simples: o jogador continua fazendo apostas "pass" ou "come" até ter pelo menos três, garantindo-as com odds completas.
Usar o sistema Three Point Molly dará ao jogador uma vantagem da casa inferior a 0,5%, o que é excelente. Isso não se deve ao sistema de apostas em si, mas sim ao fato de o jogador fazer apostas muito boas desde o início. Eu costumava jogar com esse sistema, sem saber que ele tinha um nome na época.
Regras
As regras a seguir pressupõem que o jogador conheça as regras do craps . Caso contrário, revise pelo menos as regras das apostas Pass, Come e Odds no craps antes de prosseguir.
Aqui está a versão resumida de como jogar Three Point Molly. Faça uma aposta "pass" ou "come" a cada lançamento, até cobrir três números. Apoie todas as apostas "pass" e "come" com as odds, de preferência o múltiplo máximo permitido.
A seguir, apresentamos a versão mais longa de como jogar o Three Point Molly.
O jogador terá que decidir o valor de uma unidade de aposta. Por exemplo, US$ 10. Essa unidade deverá ser, no mínimo, a aposta mínima na linha de passe. Cada aposta em passe ou em "come" corresponderá a uma unidade.
- Se for uma rodada inicial e o jogador tiver menos de três números cobertos, faça uma aposta na linha de passe.
- Se não for uma aposta inicial (come out roll) e o jogador tiver menos de três números cobertos, então faça uma aposta inicial (come bet).
- Se três números já estiverem cobertos, não faça novas apostas.
- Se uma aposta "pass" ou "come" foi feita na rodada anterior e um número de ponto (4, 5, 6, 8, 9 ou 10) foi sorteado, então aposte novamente com as odds, de preferência o máximo permitido.
- Em uma sequência de apostas iniciais (come out roll), desative as odds de quaisquer apostas iniciais pendentes.
- Continue repetindo os quatro passos acima até conseguir sete eliminações, o que marca o fim da sessão.
Análise
Para analisar o Three Point Molly, simulei mais de 32 bilhões de sessões jogando-o por computador. Presumi que o jogador sempre apostava com odds de 3, 4 e 5. Aqui estão algumas estatísticas sobre o que esperar por sessão, definida como jogar até o atirador errar o alvo (um sete).
- Média de unidades apostadas: 21,318409
- Média de unidades ganhas: -0,086295
- Proporção entre dinheiro ganho e dinheiro apostado = -0,004048
- Média dos lançamentos de dados = 8,525470
- Probabilidade de vitória na sessão = 0,304783
- Média de unidades ganhas, em caso de vitória = 15,880052
- Probabilidade de perda da sessão = 0,673288
- Média de unidades perdidas, considerando uma perda = 7,316730
- Probabilidade de envio da sessão = 0,021929
- Pontos líquidos ganhos (sem contar as apostas "come" em uma rodada inicial) = -0,688804
- Probabilidade de perder três pontos (sem contar as apostas "come" em uma rodada inicial) = 0,114039
O quadro de spoilers abaixo mostra os resultados brutos da contagem de cada vitória líquida na simulação.
Resultados da Simulação — Unidades Líquidas Ganhas
| Lucro líquido | Contar | Probabilidade |
|---|---|---|
| -28 | 2 | 0,000000 |
| -27 | 7 | 0,000000 |
| -26 | 63 | 0,000000 |
| -25 | 412 | 0,000000 |
| -24 | 2.867 | 0,000000 |
| -23 | 20.077 | 0,000001 |
| -22 | 134.791 | 0,000004 |
| -21 | 869.965 | 0,000027 |
| -20 | 5.283.822 | 0,000163 |
| -19 | 29.276.571 | 0,000905 |
| -18 | 140.054.558 | 0,004330 |
| -17 | 505.734.437 | 0,015637 |
| -16 | 847.665.043 | 0,026209 |
| -15 | 1.070.934.993 | 0,033112 |
| -14 | 670.280.254 | 0,020724 |
| -13 | 352.443.711 | 0,010897 |
| -12 | 278.945.010 | 0,008625 |
| -11 | 739.681.501 | 0.022870 |
| -10 | 1.595.074.146 | 0,049318 |
| -9 | 1.923.363.355 | 0,059469 |
| -8 | 1.717.525.038 | 0,053104 |
| -7 | 1.009.831.502 | 0,031223 |
| -6 | 860.061.437 | 0,026592 |
| -5 | 2.273.628.075 | 0,070298 |
| -4 | 2.532.516.176 | 0,078303 |
| -3 | 2.453.703.762 | 0,075866 |
| -2 | 1.590.852.863 | 0,049188 |
| -1 | 1.177.924.337 | 0,036420 |
| 0 | 709.247.041 | 0,021929 |
| 1 | 418.005.746 | 0,012924 |
| 2 | 348.914.435 | 0,010788 |
| 3 | 474.520.818 | 0,014672 |
| 4 | 659.962.642 | 0,020405 |
| 5 | 746.209.688 | 0,023072 |
| 6 | 670.131.253 | 0,020720 |
| 7 | 453.417.199 | 0,014019 |
| 8 | 281.844.697 | 0,008714 |
| 9 | 217.130.866 | 0,006713 |
| 10 | 261.596.855 | 0,008088 |
| 11 | 365.365.278 | 0,011297 |
| 12 | 431.269.636 | 0,013334 |
| 13 | 402.459.901 | 0,012444 |
| 14 | 290.068.463 | 0,008969 |
| 15 | 190.356.909 | 0,005886 |
| 16 | 148.875.109 | 0,004603 |
| 17 | 168.971.362 | 0,005224 |
| 18 | 222.536.389 | 0,006881 |
| 19 | 258.730.303 | 0,008000 |
| 20 | 243.848.069 | 0,007540 |
| 21 | 183.847.545 | 0,005684 |
| 22 | 126.712.604 | 0,003918 |
| 23 | 100.938.946 | 0,003121 |
| 24 | 109.853.273 | 0,003397 |
| 25 | 137.408.404 | 0,004249 |
| 26 | 156.412.528 | 0,004836 |
| 27 | 148.145.000 | 0,004581 |
| 28 | 115.654.061 | 0,003576 |
| 29 | 83.203.562 | 0,002573 |
| 30 | 67.504.800 | 0,002087 |
| 31 | 71.149.502 | 0,002200 |
| 32 | 85.219.705 | 0,002635 |
| 33 | 94.997.541 | 0,002937 |
| 34 | 90.199.021 | 0,002789 |
| 35 | 72.437.048 | 0,002240 |
| 36 | 54.084.552 | 0,001672 |
| 37 | 44.653.965 | 0,001381 |
| 38 | 45.923.694 | 0,001420 |
| 39 | 53.009.464 | 0,001639 |
| 40 | 57.913.108 | 0,001791 |
| 41 | 55.062.481 | 0,001702 |
| 42 | 45.282.109 | 0,001400 |
| 43 | 34.900.804 | 0,001079 |
| 44 | 29.257.203 | 0,000905 |
| 45 | 29.511.169 | 0,000912 |
| 46 | 33.021.850 | 0,001021 |
| 47 | 35.422.854 | 0,001095 |
| 48 | 33.711.968 | 0,001042 |
| 49 | 28.262.050 | 0,000874 |
| 50 | 22.384.612 | 0.000692 |
| 51 | 19.029.160 | 0,000588 |
| 52 | 18.910.013 | 0,000585 |
| 53 | 20.611.313 | 0,000637 |
| 54 | 21.741.065 | 0,000672 |
| 55 | 20.686.720 | 0,000640 |
| 56 | 17.631.119 | 0,000545 |
| 57 | 14.301.005 | 0,000442 |
| 58 | 12.314.655 | 0,000381 |
| 59 | 12.080.858 | 0,000374 |
| 60 | 12.871.214 | 0,000398 |
| 61 | 13.380.196 | 0,000414 |
| 62 | 12.720.728 | 0,000393 |
| 63 | 10.996.692 | 0,000340 |
| 64 | 9.105.439 | 0,000282 |
| 65 | 7.922.403 | 0,000245 |
| 66 | 7.700.089 | 0,000238 |
| 67 | 8.043.796 | 0,000249 |
| 68 | 8.255.742 | 0,000255 |
| 69 | 7.848.058 | 0,000243 |
| 70 | 6.865.255 | 0,000212 |
| 71 | 5.783.499 | 0,000179 |
| 72 | 5.078.376 | 0,000157 |
| 73 | 4.898.927 | 0,000151 |
| 74 | 5.034.619 | 0,000156 |
| 75 | 5.103.691 | 0,000158 |
| 76 | 4.847.033 | 0,000150 |
| 77 | 4.283.029 | 0,000132 |
| 78 | 3.660.754 | 0,000113 |
| 79 | 3.238.821 | 0,000100 |
| 80 | 3.108.409 | 0,000096 |
| 81 | 3.150.362 | 0,000097 |
| 82 | 3.165.959 | 0,000098 |
| 83 | 2.999.627 | 0,000093 |
| 84 | 2.674.553 | 0,000083 |
| 85 | 2.311.446 | 0,000071 |
| 86 | 2.062.521 | 0,000064 |
| 87 | 1.970.926 | 0,000061 |
| 88 | 1.973.623 | 0,000061 |
| 89 | 1.965.000 | 0,000061 |
| 90 | 1.861.453 | 0,000058 |
| 91 | 1.670.294 | 0,000052 |
| 92 | 1.461.087 | 0,000045 |
| 93 | 1.310.897 | 0,000041 |
| 94 | 1.247.190 | 0,000039 |
| 95 | 1.234.522 | 0,000038 |
| 96 | 1.220.060 | 0,000038 |
| 97 | 1.154.054 | 0,000036 |
| 98 | 1.044.137 | 0,000032 |
| 99 | 920.394 | 0,000028 |
| 100 | 832.175 | 0,000026 |
| 101 | 787.011 | 0,000024 |
| 102 | 773.880 | 0,000024 |
| 103 | 757.517 | 0,000023 |
| 104 | 718.633 | 0,000022 |
| 105 | 653.186 | 0,000020 |
| 106 | 580.952 | 0,000018 |
| 107 | 525.360 | 0,000016 |
| 108 | 497.143 | 0,000015 |
| 109 | 484.725 | 0,000015 |
| 110 | 472.951 | 0,000015 |
| 111 | 445.616 | 0,000014 |
| 112 | 407.531 | 0.000013 |
| 113 | 365.717 | 0,000011 |
| 114 | 332.604 | 0,000010 |
| 115 | 313.971 | 0,000010 |
| 116 | 304.434 | 0,000009 |
| 117 | 295.887 | 0,000009 |
| 118 | 278.744 | 0,000009 |
| 119 | 255.852 | 0,000008 |
| 120 | 230.156 | 0,000007 |
| 121 | 210.020 | 0,000006 |
| 122 | 198.054 | 0,000006 |
| 123 | 189.933 | 0,000006 |
| 124 | 183.510 | 0,000006 |
| 125 | 173.189 | 0,000005 |
| 126 | 159.974 | 0,000005 |
| 127 | 144.554 | 0,000004 |
| 128 | 132.215 | 0,000004 |
| 129 | 124.269 | 0,000004 |
| 130 | 119.071 | 0,000004 |
| 131 | 114.510 | 0,000004 |
| 132 | 108.716 | 0,000003 |
| 133 | 100.078 | 0,000003 |
| 134 | 91.216 | 0,000003 |
| 135 | 83.570 | 0,000003 |
| 136 | 78.006 | 0,000002 |
| 137 | 74.593 | 0,000002 |
| 138 | 72.325 | 0,000002 |
| 139 | 67.766 | 0,000002 |
| 140 | 62.234 | 0,000002 |
| 141 | 57.088 | 0,000002 |
| 142 | 52.607 | 0,000002 |
| 143 | 48.854 | 0,000002 |
| 144 | 46.992 | 0,000001 |
| 145 | 44.948 | 0,000001 |
| 146 | 42.257 | 0,000001 |
| 147 | 39.063 | 0,000001 |
| 148 | 35.878 | 0,000001 |
| 149 | 32.842 | 0,000001 |
| 150 | 30.842 | 0,000001 |
| 151 | 29.896 | 0,000001 |
| 152 | 27.741 | 0,000001 |
| 153 | 26.310 | 0,000001 |
| 154 | 24.503 | 0,000001 |
| 155 | 22.429 | 0,000001 |
| 156 | 20.836 | 0,000001 |
| 157 | 19.530 | 0,000001 |
| 158 | 18.360 | 0,000001 |
| 159 | 17.527 | 0,000001 |
| 160 | 16.597 | 0,000001 |
| 161 | 15.348 | 0,000000 |
| 162 | 13.773 | 0,000000 |
| 163 | 13.047 | 0,000000 |
| 164 | 12.509 | 0,000000 |
| 165 | 11.737 | 0,000000 |
| 166 | 10.958 | 0,000000 |
| 167 | 10.199 | 0,000000 |
| 168 | 9.501 | 0,000000 |
| 169 | 8.880 | 0,000000 |
| 170 | 8.396 | 0,000000 |
| 171 | 7.634 | 0,000000 |
| 172 | 7.399 | 0,000000 |
| 173 | 6.839 | 0,000000 |
| 174 | 6.566 | 0,000000 |
| 175 | 6.050 | 0,000000 |
| 176 | 5.745 | 0.000000 |
| 177 | 5.277 | 0,000000 |
| 178 | 4.783 | 0,000000 |
| 179 | 4.447 | 0,000000 |
| 180 | 4.378 | 0,000000 |
| 181 | 4.001 | 0,000000 |
| 182 | 3.696 | 0,000000 |
| 183 | 3.570 | 0,000000 |
| 184 | 3.243 | 0,000000 |
| 185 | 3.031 | 0,000000 |
| 186 | 2.820 | 0,000000 |
| 187 | 2.688 | 0,000000 |
| 188 | 2.599 | 0,000000 |
| 189 | 2.405 | 0,000000 |
| 190 | 2.228 | 0,000000 |
| 191 | 2.161 | 0,000000 |
| 192 | 1.867 | 0,000000 |
| 193 | 1.756 | 0,000000 |
| 194 | 1.704 | 0,000000 |
| 195 | 1.568 | 0,000000 |
| 196 | 1.439 | 0,000000 |
| 197 | 1.383 | 0,000000 |
| 198 | 1.288 | 0,000000 |
| 199 | 1.210 | 0,000000 |
| 200 | 1.117 | 0,000000 |
| 201 | 1.007 | 0,000000 |
| 202 | 942 | 0,000000 |
| 203 | 917 | 0,000000 |
| 204 | 883 | 0,000000 |
| 205 | 821 | 0,000000 |
| 206 | 719 | 0,000000 |
| 207 | 688 | 0,000000 |
| 208 | 653 | 0,000000 |
| 209 | 612 | 0,000000 |
| 210 | 559 | 0,000000 |
| 211 | 525 | 0,000000 |
| 212 | 511 | 0,000000 |
| 213 | 506 | 0,000000 |
| 214 | 435 | 0,000000 |
| 215 | 395 | 0,000000 |
| 216 | 386 | 0,000000 |
| 217 | 340 | 0,000000 |
| 218 | 336 | 0,000000 |
| 219 | 301 | 0,000000 |
| 220 | 286 | 0,000000 |
| 221 | 277 | 0,000000 |
| 222 | 251 | 0,000000 |
| 223 | 243 | 0,000000 |
| 224 | 228 | 0,000000 |
| 225 | 227 | 0,000000 |
| 226 | 179 | 0,000000 |
| 227 | 180 | 0,000000 |
| 228 | 156 | 0,000000 |
| 229 | 153 | 0,000000 |
| 230 | 142 | 0,000000 |
| 231 | 136 | 0,000000 |
| 232 | 136 | 0,000000 |
| 233 | 130 | 0,000000 |
| 234 | 127 | 0,000000 |
| 235 | 117 | 0,000000 |
| 236 | 113 | 0,000000 |
| 237 | 111 | 0,000000 |
| 238 | 77 | 0,000000 |
| 239 | 99 | 0,000000 |
| 240 | 90 | 0,000000 |
| 241 | 69 | 0,000000 |
| 242 | 74 | 0.000000 |
| 243 | 68 | 0,000000 |
| 244 | 67 | 0,000000 |
| 245 | 55 | 0,000000 |
| 246 | 56 | 0,000000 |
| 247 | 49 | 0,000000 |
| 248 | 50 | 0,000000 |
| 249 | 48 | 0,000000 |
| 250 | 38 | 0,000000 |
| 251 | 37 | 0,000000 |
| 252 | 38 | 0,000000 |
| 253 | 30 | 0,000000 |
| 254 | 23 | 0,000000 |
| 255 | 42 | 0,000000 |
| 256 | 30 | 0,000000 |
| 257 | 16 | 0,000000 |
| 258 | 24 | 0,000000 |
| 259 | 22 | 0,000000 |
| 260 | 15 | 0,000000 |
| 261 | 21 | 0,000000 |
| 262 | 20 | 0,000000 |
| 263 | 16 | 0,000000 |
| 264 | 19 | 0,000000 |
| 265 | 16 | 0,000000 |
| 266 | 10 | 0,000000 |
| 267 | 21 | 0,000000 |
| 268 | 8 | 0,000000 |
| 269 | 16 | 0,000000 |
| 270 | 9 | 0,000000 |
| 271 | 13 | 0,000000 |
| 272 | 8 | 0,000000 |
| 273 | 13 | 0,000000 |
| 274 | 7 | 0,000000 |
| 275 | 4 | 0,000000 |
| 276 | 13 | 0,000000 |
| 277 | 9 | 0,000000 |
| 278 | 5 | 0,000000 |
| 279 | 13 | 0,000000 |
| 280 | 4 | 0,000000 |
| 281 | 4 | 0,000000 |
| 282 | 3 | 0,000000 |
| 283 | 12 | 0,000000 |
| 284 | 6 | 0,000000 |
| 285 | 2 | 0,000000 |
| 286 | 7 | 0,000000 |
| 287 | 2 | 0,000000 |
| 288 | 3 | 0,000000 |
| 290 | 4 | 0,000000 |
| 291 | 1 | 0,000000 |
| 292 | 5 | 0,000000 |
| 294 | 1 | 0,000000 |
| 295 | 2 | 0,000000 |
| 296 | 5 | 0,000000 |
| 297 | 1 | 0,000000 |
| 298 | 1 | 0,000000 |
| 299 | 4 | 0,000000 |
| 300 | 2 | 0,000000 |
| 302 | 4 | 0,000000 |
| 303 | 1 | 0,000000 |
| 305 | 1 | 0,000000 |
| 307 | 1 | 0,000000 |
| 309 | 1 | 0,000000 |
| 310 | 1 | 0,000000 |
| 311 | 1 | 0,000000 |
| 312 | 1 | 0,000000 |
| 313 | 1 | 0,000000 |
| 316 | 1 | 0,000000 |
| 317 | 1 | 0,000000 |
| 318 | 1 | 0.000000 |
| 322 | 1 | 0,000000 |
| 345 | 1 | 0,000000 |
| Total | 32.342.500.000 | 1.000000 |
O gráfico a seguir mostra a probabilidade de um ganho líquido de -25 a +100 unidades.
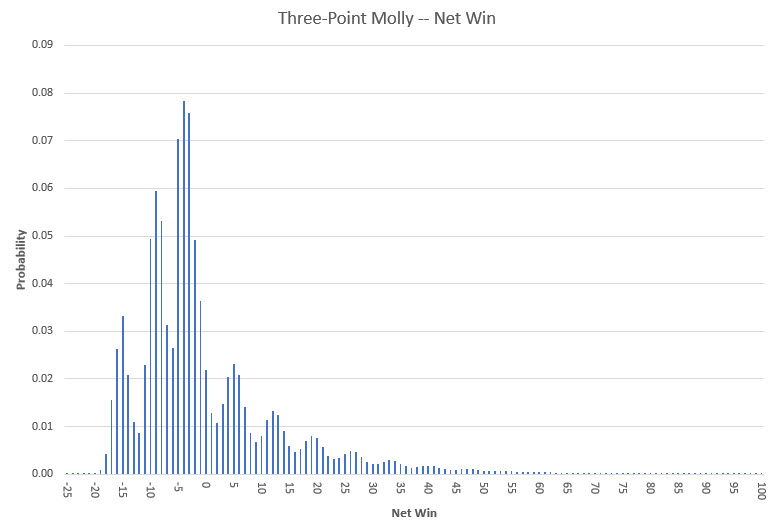
Realizei uma simulação separada de 7,6 bilhões de sessões que analisou os pontos líquidos ganhos, sem contabilizar as vitórias em uma rodada inicial (porque as probabilidades estavam desativadas). O botão de spoiler abaixo mostra os resultados.
Resultados da simulação — Pontos líquidos ganhos
| Líquido Pontos Ganho | Contar | Probabilidade |
|---|---|---|
| -3 | 866.696.937 | 0,114039 |
| -2 | 1.799.063.609 | 0,236719 |
| -1 | 2.707.830.104 | 0,356293 |
| 0 | 859.942.908 | 0,113150 |
| 1 | 509.181.625 | 0,066998 |
| 2 | 318.786.035 | 0,041946 |
| 3 | 200.282.777 | 0,026353 |
| 4 | 125.828.052 | 0,016556 |
| 5 | 79.035.018 | 0,010399 |
| 6 | 49.629.205 | 0,006530 |
| 7 | 31.167.223 | 0,004101 |
| 8 | 19.559.543 | 0,002574 |
| 9 | 12.280.517 | 0,001616 |
| 10 | 7.710.235 | 0,001015 |
| 11 | 4.842.391 | 0,000637 |
| 12 | 3.039.626 | 0,000400 |
| 13 | 1.907.701 | 0,000251 |
| 14 | 1.197.193 | 0,000158 |
| 15 | 751.657 | 0,000099 |
| 16 | 471.330 | 0,000062 |
| 17 | 296.874 | 0,000039 |
| 18 | 186.123 | 0,000024 |
| 19 | 116.693 | 0,000015 |
| 20 | 73.449 | 0,000010 |
| 21 | 45.690 | 0,000006 |
| 22 | 28.787 | 0,000004 |
| 23 | 18.141 | 0,000002 |
| 24 | 11.410 | 0,000002 |
| 25 | 7.248 | 0,000001 |
| 26 | 4.395 | 0,000001 |
| 27 | 2.775 | 0,000000 |
| 28 | 1.759 | 0,000000 |
| 29 | 1.081 | 0,000000 |
| 30 | 714 | 0,000000 |
| 31 | 426 | 0,000000 |
| 32 | 276 | 0,000000 |
| 33 | 182 | 0,000000 |
| 34 | 98 | 0,000000 |
| 35 | 69 | 0,000000 |
| 36 | 40 | 0,000000 |
| 37 | 31 | 0,000000 |
| 38 | 20 | 0,000000 |
| 39 | 17 | 0,000000 |
| 40 | 8 | 0,000000 |
| 41 | 2 | 0,000000 |
| 42 | 4 | 0,000000 |
| 43 | 1 | 0,000000 |
| 45 | 1 | 0,000000 |
| Total | 7.600.000.000 | 1.000000 |
Vídeo
Por favor, aproveite meu vídeo sobre a Molinésia de Três Pontos.
Aprimorando o Three Point Molly
O jogador pode reduzir a vantagem da casa de 0,405% para 0,374% mantendo as probabilidades de uma aposta "come" ativas em uma rodada inicial (come out roll).
Conclusão
O que importa nas apostas é o jogo em si, a aposta feita e, às vezes, sua habilidade em tomar decisões. O que não importa é o motivo da aposta. Por isso, os sistemas de apostas não são mágica matemática que aumentam as chances de vitória para o jogador. Não, os sistemas de apostas não apenas não reduzem a vantagem da casa, como sequer a diminuem.
O grande trunfo do Three Point Molly não é o método em si, mas sim o fato de ser jogado com uma vantagem da casa muito baixa. As apostas Pass e Come têm uma vantagem da casa de 1,41%, enquanto todas as apostas de odds têm uma vantagem da casa de 0,00%. Fazendo uma média ponderada, a vantagem da casa total é de 0,40%. É difícil superar isso em um cassino.
Links internos
Three Point Dolly — A versão maligna da Three Point Molly, baseada em criar uma situação de "não passe, não venha" e apostar todas as fichas. As probabilidades são ainda melhores do que na Three Point Molly, mas você terá que aguentar os olhares de reprovação nas mesas.
Links externos
Discussão sobre o Three Point Molly no meu fórum no Wizard of Vegas.


