Nesta página
Como é calculada a vantagem da casa em cada aposta
Introdução
Bem-vindo ao apêndice de craps. Aqui, calculo a vantagem do jogador para todas as principais apostas no craps. Fora deste apêndice, geralmente falo sobre a vantagem da casa, que é simplesmente o produto da vantagem do jogador por -1. Para evitar multiplicar por -1 para cada aposta, falarei de tudo em termos da vantagem do jogador, que você pode esperar que seja negativa, já que a casa tem vantagem em todas as apostas, exceto nas apostas grátis. Fique um pouco e pratique um pouco com algumas das apostas. Isso não só lhe dará uma compreensão mais profunda das probabilidades, como também, espero, o motivará a relembrar ou aprimorar suas habilidades matemáticas.
Antes de prosseguir, você precisa entender a probabilidade de obter cada total em um único lançamento. Isso é explicado detalhadamente na minha página sobre fundamentos de probabilidade com dados . Se você não sabia ou não consegue calcular que a probabilidade de rolar um 6 é 5/36, então uma visita a essa página é um pré-requisito para esta.
A fórmula geral para o retorno esperado de uma aposta é:
∑ (probabilidade do evento i) × (retorno do evento i) sobre todos os resultados possíveis.
A vantagem do jogador é o retorno esperado dividido pela aposta inicial. Por exemplo, ao apostar contra a linha em um evento esportivo, você precisa apostar $11 para ganhar $10. Supondo uma chance de 50% de ganhar, o retorno esperado seria 0,5 × (10) + 0,5 × (-11) = -0,5. A vantagem do jogador seria -0,5/11 = -1/22 ≈ -4,545%.
Uma exceção à regra da vantagem da casa ocorre quando um empate é possível. Em geral, os empates são ignorados nos cálculos da vantagem da casa. Para compensar isso, quando um empate é possível, divide-se o retorno esperado pela aposta média resolvida. A "aposta média resolvida" é o produto da aposta inicial e da probabilidade de a aposta ter sido resolvida. No craps, as únicas apostas com empate são "don't pass" e "don't come".
Muitas das apostas no craps ganham se um evento específico ocorrer antes de outro. Essas apostas podem levar várias rodadas ou mais para serem resolvidas. Se uma aposta ganha com probabilidade p, perde com probabilidade q e permanece ativa com probabilidade 1-pq, então a probabilidade de ganhar eventualmente é:
∑ p×(1-pq) i (para i=0 até infinito) =
p × (1/(1-(1-pq))) = p × (1/(p+q)) = p/(p+q).
Ao longo desta página, você verá muitas expressões da forma p/(p+q). Para economizar espaço, não vou demonstrar a expressão a cada vez, pois ela já foi calculada acima.
Passar/Vir
A probabilidade de ganhar no lançamento inicial é pr(7)+pr(11) = 6/36 + 2/36 = 8/36.
A probabilidade de estabelecer um ponto e depois vencer é pr(4)×pr(4 antes de 7) + pr(5)×pr(5 antes de 7) + pr(6)×pr(6 antes de 7) + pr(8)×pr(8 antes de 7) + pr(9)×pr(9 antes de 7) + pr(10)×pr(10 antes de 7) =
(3/36)×(3/9) + (4/36)×(4/10) + (5/36)×(5/11) + (5/36)×(5/11) + (4/36)×(4/10) + (3/36)×(3/9) =
(2/36) × (9/9 + 16/10 + 25/11) =
(2/36) × (990/990 + 1584/990 + 2250/990) =
(2/36) × (4824/990) = 9648/35640
A probabilidade total de ganhar é 8/36 + 9648/35640 = 17568/35640 = 244/495
A probabilidade de perder é obviamente 1-(244/495) = 251/495
A vantagem do jogador é, portanto, (244/495)×(+1) + (251/495)×(-1) = -7/495 ≈ -1,414%.
Não passe/Não venha
A probabilidade de ganhar no lançamento inicial é pr(2)+pr(3) = 1/36 + 2/36 = 3/36.
A probabilidade de empatar no lançamento de saída é pr(12) = 1/36.
A probabilidade de estabelecer um ponto e depois vencer é pr(4)×pr(7 antes de 4) + pr(5)×pr(7 antes de 5) + pr(6)×pr(7 antes de 6) + pr(8)×pr(7 antes de 8) + pr(9)×pr(7 antes de 9) + pr(10)×pr(7 antes de 10) =
(3/36)×(6/9) + (4/36)×(6/10) + (5/36)×(6/11) + (5/36)×(6/11) + (4/36)×(6/10) + (3/36)×(6/9) =
(2/36) × (18/9 + 24/10 + 30/11) =
(2/36) × (1980/990 + 2376/990 + 2700/990) =
(2/36) × (7056/990) = 14112/35640
A probabilidade total de ganhar é 3/36 + 14112/35640 = 17082/35640 = 2847/5940
A probabilidade de perder é 1-(2847/5940 + 1/36) = 1-(3012/5940) = 2928/5940
O retorno esperado é 2847/5940×(+1) + 2928/5940×(-1) = -81/5940 = -3/220 ≈ 1,364%
A maioria das outras fontes sobre craps afirma que a vantagem da casa na aposta "don't pass" é de 1,403%. A origem da discrepância reside em se os empates devem ou não ser contabilizados. Eu prefiro contabilizá-los como apostas em dinheiro, enquanto outros não. Não estou dizendo que um lado está certo ou errado, apenas que prefiro contabilizá-los.Se você não considerar empates como apostas em dinheiro, então deve dividir o valor acima pela probabilidade de a aposta ser resolvida em vitória ou derrota (35/36). Portanto, 1,364%/(35/36) ≈ -1,403%. Esta é a vantagem da casa, assumindo que o jogador nunca tire um 12 na primeira jogada.
Faça suas apostas para ganhar
Faça a aposta em 6 ou 8: [(5/11)×7 + (6/11)×(-6)]/6 = (-1/11)/6 = -1/66 ≈ -1,515%
Faça a aposta em 5 ou 9: [(4/10)×7 + (6/10)×(-5)]/5 = (-2/10)/5 = -1/25 = -4,000%
Faça a aposta em 4 ou 10: [(3/9)×9 + (6/9)×(-5)]/5 = (-3/9)/5 = -1/15 ≈ -6,667%
Faça apostas para perder
Faça uma aposta para perder no 6 ou no 8: [(6/11)×4 + (5/11)×(-5)]/5 = (-1/11)/5 = -1/55 ≈ -1,818%
Faça uma aposta para perder em 5 ou 9: [(6/10)×5 + (4/10)×(-8)]/8 = (-2/10)/8 = -1/40 = -2,500%
Faça uma aposta para perder no 4 ou no 10: [(6/9)×5 + (3/9)×(-11)]/11 = (-3/9)/11 = -1/33 ≈ -3,030%
Observação: Essas apostas não são permitidas em cassinos físicos. Elas só podem ser encontradas em alguns cassinos online.
Comprar
Aposte em 6 ou 8: [(5/11)×23 + (6/11)×(-21)]/21 = (-11/11)/21 = -1/21 ≈ -4,762%
Aposte em 5 ou 9: [(4/10)×29 + (6/10)×(-21)]/21 = (-10/10)/21 = -1/21 = -4,762%
Aposte em 4 ou 10: [(3/9)×39 + (6/9)×(-21)]/21 = (-9/9)/21 = -1/21 ≈ -4,762%
Deitar
Aposta contra para perder em 6 ou 8: [(6/11)×19 + (5/11)×(-25)]/25 = (-11/11)/25 = -1/25 ≈ -4,000%
Aposta contra para perder em 5 ou 9: [(6/10)×19 + (4/10)×(-31)]/31 = (-10/10)/31 = -1/31 = -3,226%
Aposta contra para perder em 4 ou 10: [(6/9)×19 + (3/9)×(-41)]/41 = (-9/9)/41 = -1/41 ≈ -2,439%
Big 6/Big 8
[(5/11)×1 + (6/11)×(-1)]/1 = -1/11 ≈ 9,091%
Difícil 4/Difícil 10
Observação: O 4 duro e o 10 duro pagam 7 para 1, ou 8 para 1. No craps, as probabilidades do pano são listadas com base em 1 para 1, incluindo o gráfico acima.
A probabilidade de se obter um 4 rígido em qualquer lançamento de dado é de 1/36.
A probabilidade de sair um 7 em qualquer lançamento de dado é de 6/36.
A probabilidade de um 4 suave em qualquer lançamento de dado é 2/36 (1+3 e 3+1).
A probabilidade de ganhar em qualquer lançamento de dado é de 1/36.
A probabilidade de perder em qualquer lançamento de dado é 6/36 + 2/36 = 8/36.
A probabilidade de ganhar a aposta é p/(p+q) (veja acima) = (1/36)/(9/36) = 1/9
O retorno esperado é (1/9)×7 + (8/9)×(-1) = -1/9 ≈ 11,111%.
A vantagem do jogador também é de -1/9, já que a aposta é de 1 unidade.
As probabilidades são as mesmas para um 10 difícil.
Difícil 6/Difícil 8
Observação: O 4 duro e o 10 duro pagam 9 para 1, ou 10 para 1. No craps, as probabilidades do pano são listadas com base em 1 para 1, incluindo o gráfico acima.
A probabilidade de se obter um 6 rígido em qualquer lançamento de dado é de 1/36.
A probabilidade de sair um 7 em qualquer lançamento de dado é de 6/36.
A probabilidade de um 6 suave em qualquer lançamento dado é 4/36 (1+5, 2+3, 3+2 e 5+1).
A probabilidade de ganhar em qualquer lançamento de dado é de 1/36.
A probabilidade de perder em qualquer lançamento de dado é 6/36 + 4/36 = 10/36.
A probabilidade de ganhar a aposta é p/(p+q) (veja acima) = (1/36)/(11/36) = 1/11
O retorno esperado é (1/11)×9 + (10/11)×(-1) = -1/11 ≈ 9,091%.
A vantagem do jogador também é de -1/11, já que a aposta é de 1 unidade.
As probabilidades são as mesmas para um 8 difícil.
Craps 2/Craps 12
[(1/36)×30 + (35/36)×(-1)]/1 = -5/36 ≈ -13,889%
Craps 3/Craps 11
[(2/36)×15 + (34/36)×(-1)]/1 = -4/36 ≈ -11,111%
Qualquer Craps
[(4/36)×7 + (32/36)×(-1)]/1 = -4/36 ≈ -11,111%
Quaisquer 7
[(6/36)×4 + (30/36)×(-1)]/1 = -6/36 ≈ -16,667%
Buzina
A probabilidade de tirar um 2 ou um 12 nos dados é 1/36 + 1/36 = 2/36.
A probabilidade de tirar um 3 ou um 11 nos dados é 2/36 + 2/36 = 4/36.
A probabilidade de rolar qualquer outro número é 1-2/36-4/36 = 30/36.
Lembre-se que a aposta Horn é como se fossem todas as quatro apostas do craps em uma só. Mesmo que uma ganhe, as outras três ainda perdem. A vantagem da casa é:
[(2/36)×27 + (4/36)×12 + (30/36)×(-4)]/4 = (-18/36)/4 = 12,500%
Campo
Quando o jogo 12 paga 2:1, o retorno esperado é:
2×(pr(2)+pr(12)) + 1×(pr(3)+pr(4)+pr(5)+pr(10)+pr(11)) + -1×(pr(6)+pr(7)+pr(8)+pr(9)) =
2×(1/36 + 1/36) + 1×(2/36 + 3/36 + 4/36 + 3/36 + 2/36) + -1×(5/36 + 6/36 + 5/36 + 4/36) =
2×(2/36) + 1×(14/36) + -1×(20/36) = -2/36 = -1/18 ≈ 5,556%.
Quando o jogo 12 paga 3:1, o retorno esperado é:
3×pr(2) + 2×pr(12)) + 1×(pr(3)+pr(4)+pr(5)+pr(10)+pr(11)) + -1×(pr(6)+pr(7)+pr(8)+pr(9)) =
3×(1/36) + 2×(1/36) + 1×(2/36 + 3/36 + 4/36 + 3/36 + 2/36) + -1×(5/36 + 6/36 + 5/36 + 4/36) =
3×(1/36) + 2×(1/36) + 1×(14/36) + -1×(20/36) = -1/36 ≈ 2,778%.
Probabilidades de compra
4 e 10: [(3/9)×2 + (6/9)×(-1)]/1 = 0,000%
5 e 9: [(4/10)×3 + (6/10)×(-2)]/2 = 0,000%
6 e 8: [(5/11)×6 + (6/11)×(-5)]/5 = 0,000%
Apostar em probabilidades
4 e 10: [(6/9)×1 + (3/9)×(-2)]/1 = 0,000%
5 e 9: [(6/10)×2 + (4/10)×(-3)]/2 = 0,000%
6 e 8: [(6/11)×5 + (5/11)×(-6)]/5 = 0,000%
Probabilidades combinadas de passe e compra
A vantagem do jogador na combinação de apostas na linha de passe e na compra de odds é o ganho médio do jogador dividido pela aposta média do jogador. O ganho na linha de passe é sempre -7/495 e o ganho nas odds é sempre 0. A aposta esperada depende do múltiplo de odds permitido. Vamos supor odds dobradas, ou seja, que a aposta na linha de passe seja de $2, a aposta nas odds em 4, 5, 9 e 10 seja de $4 e a aposta nas odds em 6 ou 8 seja de $5.
O ganho médio é -2×(7/495) = -14/495.
A aposta média é 2 + (3/36)×4 + (4/36)×4 + (5/36)×5 + (5/36)×5 + (4/36)×4 + (3/36)×4] =
2 + 106/36 = 178/36
A vantagem do jogador é (-14/495)/(178/36) = -0,572%.
A fórmula geral, se você puder multiplicar x pelas probabilidades do 6 e do 8, y pelas do 5 e do 9 e z pelas do 4 e do 10, é (-7 / 495) / [ 1 + ((5x + 4y + 3z) / 18) ]
Combinação de "Não Passe" e "Apostar Contra"
A vantagem do jogador na combinação de "don't pass" e "lay" é o ganho médio do jogador dividido pela aposta média do jogador. O ganho no "don't pass" é sempre -3/220 e o ganho no "lay" é sempre 0. A aposta esperada depende do múltiplo de odds permitido. Vamos supor odds dobradas e uma aposta "don't pass" de $10. Então, o jogador pode apostar $40 contra odds para um ganho de $20 nos números 4 e 10, $30 contra um ganho de $20 nos números 5 e 9, e $24 contra um ganho de $20 nos números 6 e 8. O ganho médio é -10 × (3/220) = -30/220.
A aposta média é 10 + 2×[(3/36)×40 + (4/36)×30 + (5/36)×24] = 30.
A vantagem do jogador é (-30/220)/30 = -0,455%.
A fórmula geral, se você puder comprar x vezes as probabilidades, então a vantagem da casa na combinação de não passar e apostar contra é (3/220)/(1+x).
Lucro/Prejuízo Líquido por Sessão
O gráfico abaixo mostra o ganho ou perda líquida que você pode esperar ao longo de 100 tentativas, ou lançamentos iniciais. Para fins de criação do gráfico, o jogador apostaria $1 na linha de passe e receberia o dobro das probabilidades.
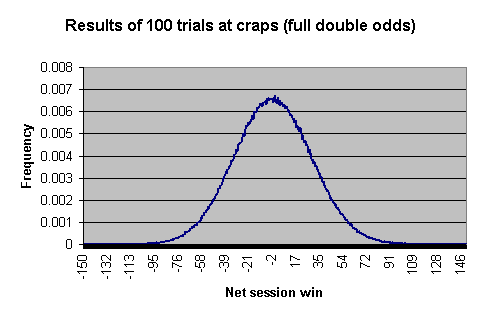
Aqui estão alguns números reais que mostram a probabilidade de se enquadrar em vários intervalos.
Vitórias/Derrotas da Sessão
| Intervalo | Probabilidade |
|---|---|
| prejuízo de mais de 100 dólares | 0,0422% |
| prejuízo de $76 a $100 | 0,6499% |
| prejuízo de $51 a $75 | 4,6414% |
| prejuízo de $26 a $50 | 16,3560% |
| perda de $1 a $25 | 30,0583% |
| empatar | 0,6743% |
| Prêmio de $1 a $25 | 28,6368% |
| Prêmio de $26 a $50 | 14,4257% |
| Prêmio de $51 a $75 | 3,9097% |
| ganho de $76 a $100 | 0,5639% |
| ganho de mais de 100 dólares | 0,0418% |
O gráfico e a tabela foram criados simulando 1.000.000 de sessões de 100 tentativas, ou lançamentos de dados, e tabulando os resultados de cada sessão.
Links internos
- Em resumo, como se calcula a vantagem da casa em cada aposta .
- A vantagem da casa em todas as principais apostas, tanto por aposta realizada quanto por rodada.
- Experimentos de Controle de Dados. Os resultados de dois experimentos sobre o lançamento habilidoso de dados.
- Vantagem do Controle dos Dados. A vantagem do jogador, assumindo que ele possa influenciar os dados.
- Variantes do Craps . Regras e apostas alternativas, como a Fire Bet, o Crapless Craps e o Card Craps.
- Craps na Califórnia . Como se joga craps na Califórnia usando cartas de baralho.
- Jogue Craps . Jogo de Craps com cartas no cassino Viejas em San Diego.
- Tabela de Número de Lançamentos . Probabilidade de um lançador durar de 1 a 200 lançamentos antes de tirar um sete.
- Pergunte ao Mago. Veja as perguntas sobre craps que eu respondi:
- Jogo de Craps simples. Meu jogo de Craps simples em Java.


