Nesta página
Craps Bônus
Introdução
O Bonus Craps é um conjunto de três apostas paralelas encontradas no jogo de craps. São elas:
- Pequeno — Ganha se o lançador rolar todos os totais de 2 a 6, antes de rolar um total de 7. As vitórias geralmente pagam 30 para 1.
- Alto — Ganha se o lançador rolar todos os totais de 8 a 12, antes de rolar um total de 7. As vitórias geralmente pagam 30 para 1.
- Todos — Ganha se o lançador rolar todos os totais de 2 a 12, exceto 7, antes de rolar um total de 7. As vitórias geralmente pagam 150 para 1.
Em 2021, comecei a ver essas mesmas apostas chamadas "Diceologia" no Venetian.
Análise
A tabela a seguir mostra minha análise das apostas Small e Tall, quando os ganhos pagam 30 para 1. A célula inferior direita mostra uma vantagem da casa de 18,30%.
Pequeno e Alto
| Evento | Paga | Probabilidade | Retornar |
|---|---|---|---|
| Ganhar | 30 | 0,026354 | 0,790617 |
| Perda | -1 | 0,973646 | -0,973646 |
| Total | 1.000000 | -0,183029 |
Antigamente, algumas mesas chegavam a pagar 34 para 1 no Small and Tall. Essas probabilidades mais generosas representam uma vantagem da casa de 7,76%.
A tabela a seguir mostra minha análise da aposta "All", quando os ganhos pagam 150 para 1. A célula inferior direita mostra uma vantagem da casa de 20,61%.
Todos
| Evento | Paga | Probabilidade | Retornar |
|---|---|---|---|
| Ganhar | 150 | 0,005258 | 0,788655 |
| Perda | -1 | 0,994742 | -0,994742 |
| Total | 1.000000 | -0,206087 |
Já vi outros pagamentos na aposta "All", incluindo 155 e 175 para 1. Lembre-se de subtrair um do pagamento para converter de "para um" para "para um". A tabela a seguir mostra a vantagem da casa para todos os pagamentos divisíveis por 5, de 150 a 175.
Resumo da vantagem da casa no All Bet
| Paga | Borda da casa |
|---|---|
| 150 | 20,61% |
| 155 | 17,98% |
| 160 | 15,35% |
| 165 | 12,72% |
| 170 | 10,09% |
| 175 | 7,46% |
Metodologia
Analisei o Bonus Craps de três maneiras, como segue:
- Simulação — Este é provavelmente o caminho mais fácil. No entanto, para puristas da matemática como eu, as simulações são sempre intelectualmente insatisfatórias.
- Cadeia de Markov — Este método é trabalhoso e demorado. Para os casos Pequeno e Alto, seria necessária uma matriz de transição 6x6 e, para o caso Todos, uma matriz 12x12.
- Cálculo Integral — Este método é surpreendentemente fácil com o uso de uma calculadora de integrais. Explico-o com mais detalhes abaixo.
Imagine que, em vez de eventos significativos serem determinados pelo lançamento de dados, um de cada vez, considere-os como um instante no tempo. Suponha que o tempo entre os eventos tenha uma propriedade de ausência de memória, com um tempo médio entre eventos de uma unidade de tempo. Em outras palavras, o tempo entre os eventos segue uma distribuição exponencial com média de 1. Isso não importará para fins de arbitragem da aposta, porque os eventos ainda acontecem um de cada vez.
A seguir, apresenta-se a probabilidade de um determinado total NÃO ter sido obtido pelo menos uma vez dentro de x unidades de tempo:
- 2 ou 12: exp(-x/36)
- 3 ou 11: exp(-x/18)
- 4 ou 10: exp(-x/12)
- 5 ou 9: exp(-x/9)
- 6 ou 8: exp(-5x/36)
- 7: exp(-x/6)
Vamos analisar primeiro a aposta Pequena. As probabilidades são exatamente as mesmas da aposta Alta.
Em x unidades de tempo, a probabilidade de que os números 2, 3, 4, 5 e 6 tenham sido rolados, e o 7 não, é: (1-exp(-x/36))*(1-exp(-x/18))*(1-exp(-x/12))*(1-exp(-x/9))*(1-exp(-5x/36))*exp(-x/6). A probabilidade de que, no instante x, o jogador role um 7, tendo anteriormente rolado todos os totais de 2 a 6, é:
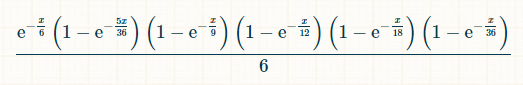
Para a integração, utilizei esta calculadora de integrais .
Como um 7 vencedor pode acontecer a qualquer momento, a probabilidade de ganhar é a integral dessa probabilidade em relação a x, de 0 ao infinito. Não que precisemos saber, mas a integral, antes de impor os limites de integração, é (-6*e^(-x/6)+(36*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-(36*e^ (-(11*x)/36))/11-3*e^(-x/3)-(36*e^(-(13*x)/36))/13+(18*e^(- (7*x)/18))/7+(12*e^(-(5*x)/12))/5+(9*e^(-(4*x)/9))/4-(36*e^ (-(19*x)/36))/19-(9*e^(-(5*x)/9))/5+(12*e^(-(7*x)/12))/7)/6.
Considerando os limites de integração, a resposta é 20049 / 760760 = aproximadamente 0,02635390924864609.
Em seguida, vamos analisar a aposta "All".
Em x unidades de tempo, a probabilidade de que os números 2, 3, 4, 5, 6, 8, 9, 10, 11 e 12 tenham sido rolados, e o 7 não tenha sido, é: (1-exp(-x/36)) ² * (1-exp(-x/16)) ² * (1-exp(-x/12)) ² * (1-exp(-x/9)) ² * (1-exp(-5x/36)) ² * exp(-x/6). A probabilidade de que, no instante x, o jogador role um 7, tendo anteriormente rolado todos os totais de 2 a 6, é:
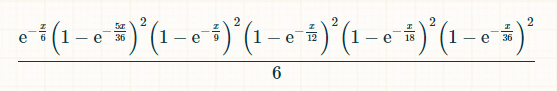
Como um 7 vencedor pode ocorrer a qualquer momento, a probabilidade de ganhar é a integral dessa probabilidade em relação a x, de 0 ao infinito. Não que precisemos saber, mas a integral, antes de aplicar os limites de integração, é (-6*e^(-x/6)+(72*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-8*e^(-x/4)-(18*e^(-(5*x)/18))/5-(72*e^(-(11*x)/36))/11+(72*e^(-(13*x)/36))/13+(108*e^(-(7*x)/1) 8))/7+(24*e^(-(5*x)/12))/5-(27*e^(-(4*x)/9))/4-(216*e^(-(17*x)/36))/17-10* e^(-x/2)-(72*e^(-(19*x)/36))/19+(27*e^(-(5*x)/9))/5+(144*e^(-(7*x)/12))/7+ (54*e^(-(11*x)/18))/11-(72*e^(-(23*x)/36))/23-(15*e^(-(2*x)/3))/2-(216*e^( -(25*x)/36))/25-(54*e^(-(13*x)/18))/13+(8*e^(-(3*x)/4))/3+(54*e^(-(7*x)/9) )/7+(72*e^(-(29*x)/36))/29-(72*e^(-(31*x)/36))/31-(9*e^(-(8*x)/9))/8-(24*e ^(-(11*x)/12))/11+(18*e^(-(17*x)/18))/17+(72*e^(-(35*x)/36))/35-e^(-x))/6.
Colocando os limites de integração, a resposta é 126538525259 / 24067258815600 = 0,0052577040961964420049.



