Nesta página
Duplas diferentes
Introdução
O Different Doubles é uma aposta paralela de craps que pode ser vista no cassino Beau Rivage em Biloxi. Ela paga com base no número de pares diferentes que o lançador consegue antes de atingir um total de sete. A tabela de pagamentos é a seguinte:
- 6 apostas duplas pagam 100 para 1
- 5 apostas duplas pagam 15 para 1.
- 4 apostas duplas pagam 8 para 1
- 3 apostas duplas pagam 4 para 1
Análise
A tabela abaixo mostra a probabilidade e a contribuição para o retorno de todos os resultados possíveis. A célula inferior direita mostra uma vantagem da casa de 27,92% (ai!).
Diferentes tabelas de retorno de duplas
| Duplas Feitas | Paga | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| 6 | 100 | 1 | 0,001082 | 0,108225 |
| 5 | 15 | 6 | 0,006494 | 0,097403 |
| 4 | 8 | 21 | 0,022727 | 0,181818 |
| 3 | 4 | 56 | 0,060606 | 0,242424 |
| 2 | -1 | 126 | 0,136364 | -0,136364 |
| 1 | -1 | 252 | 0,272727 | -0,272727 |
| 0 | -1 | 462 | 0,500000 | -0,500000 |
| Total | 924 | 1.000000 | -0,279221 |
Análise Algébrica
A probabilidade de qualquer par é 1/36. Portanto, a probabilidade de QUALQUER par é 6/36 = 1/6. A probabilidade de qualquer sete é 1/6. Podemos ignorar todos os lançamentos, exceto pares e setes. Assim, supondo que tenha havido um lançamento pertinente à aposta, abaixo estão as probabilidades para esse lançamento:
- Qualquer valor duplo = 1/2
- Qualquer sete = 1/2
A probabilidade de o primeiro lançamento significativo ser um sete é 1/2. Portanto, a probabilidade de não haver números iguais é zero.
Caso contrário, o jogador teria tirado um par de dados iguais. Podemos agora ignorar a possibilidade de tirar esse par de dados novamente como um evento significativo. As probabilidades de ambos os tipos de eventos significativos são agora:
- Qualquer duplicação significativa = 5/11
- Qualquer sete = 6/11
A probabilidade de o jogador rolar um sete neste ponto, para um par, é 6/11. Assim, a probabilidade geral de um par é (1/2)*(6/11) = 3/11 = aproximadamente 27,27%.
Caso contrário, o jogador teria tirado um segundo par. Podemos agora ignorar a possibilidade de tirar dois pares distintos como um evento significativo. As probabilidades de ambos os tipos de eventos significativos são agora:
- Qualquer duplicação significativa = 4/10
- Qualquer sete = 6/10
A probabilidade de o jogador rolar um sete neste ponto, para dois pares, é 6/10. Assim, a probabilidade geral de um par é (1/2)*(5/11)*(6/10) = 3/22 = aproximadamente 13,6363636%.
Caso contrário, o jogador teria tirado um terceiro par. Podemos agora ignorar a possibilidade de tirar três pares distintos como um evento significativo. As probabilidades de ambos os tipos de eventos significativos são agora:
- Qualquer duplicação significativa = 3/9
- Qualquer sete = 6/9
A probabilidade de o jogador rolar um sete neste ponto, para dois pares, é 6/9. Assim, a probabilidade geral de um par é (1/2)*(5/11)*(4/10)*(6/9) = 2/33 = aproximadamente 6,060606%.
Caso contrário, o jogador teria tirado um quarto par. Podemos agora ignorar a possibilidade de tirar quatro pares distintos como um evento significativo. As probabilidades de ambos os tipos de eventos significativos são agora:
- Qualquer duplicação significativa = 2/8
- Qualquer sete = 6/8
A probabilidade de o jogador rolar um sete neste ponto, para dois pares, é 6/8. Assim, a probabilidade geral de um par é (1/2)*(5/11)*(4/10)*(3/9)*(6/8) = 1/44 = aproximadamente 2,272727%.
Caso contrário, o jogador teria tirado um quinto par. Podemos agora ignorar a possibilidade de tirar cinco pares distintos como um evento significativo. As probabilidades de ambos os tipos de eventos significativos são agora:
- Qualquer duplicação significativa = 1/7
- Qualquer sete = 6/7
A probabilidade de o jogador rolar um sete neste ponto, para obter dois pares, é 6/7. Assim, a probabilidade geral de um par é (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(6/7) = 1/154 = aproximadamente 0,649351%.
Caso contrário, o jogador teria tirado o último par restante. A probabilidade disso é (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(1/7) = 1/924 = aproximadamente 0,108225%.
Agora podemos juntar tudo isso na tabela de resultados acima. O número de combinações possíveis é de 924.
Análise de Cálculo Integral
Imagine que, em vez de eventos significativos serem determinados pelo lançamento de dados, um de cada vez, considere-os como um instante no tempo. Suponha que o tempo entre os eventos tenha uma propriedade de ausência de memória, com um tempo médio entre eventos de uma unidade de tempo. Em outras palavras, o tempo entre os eventos segue uma distribuição exponencial com média de 1. Isso não importará para fins de arbitragem da aposta, porque os eventos ainda acontecem um de cada vez.
O intervalo de tempo entre duplicatas específicas seguirá uma distribuição exponencial com média de 12. O motivo para o valor 12 é que, se houver um evento significativo, existe uma probabilidade de 1/12 de que tenha sido aquela duplicata específica. Portanto, a probabilidade de uma duplicata específica não ter ocorrido em x unidades de tempo é exp(-x/12). A probabilidade de ela ter ocorrido é, portanto, 1-exp(-x/12).
Seja x o número de unidades de tempo desde o início da aposta. A probabilidade de que todos os pares tenham ocorrido e nenhum sete tenha ocorrido é (1-exp(-x/12)) 6 × exp(-x/2).
Para finalizar com um lançamento de 7 no instante x, multiplique isso por 1/2, a probabilidade de um 7, para obter uma probabilidade de ganhar exatamente no instante x de (1/2) × (1 - exp(-x/12)) 6 × exp(-x/2)
Para encontrar a probabilidade de uma aposta ser vencedora ao longo de todo o tempo, integre de 1 ao infinito:
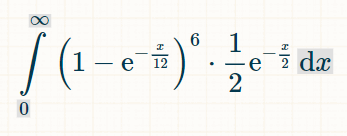
Para integrar isso, recomendo esta calculadora de integrais . No campo de integral, digite "(1-exp(-x/12))^6*(1/2)*exp(-x/2)." Para os limites de integração, em opções, digite 0 e ∞. Em seguida, clique em "ir".Isso lhe dará a integral abaixo:
(-(1-e^(-x/12))^12+(60*(1-e^(-x/12))^11)/11-12*(1-e^(-x/12))^10+(40 *(1-e^(-x/12))^9)/3-(15*(1-e^(-x/12))^8)/2+(12*(1-e^(-x/12))^7)/7)/2
No entanto, não precisamos inserir 0. A calculadora fornece a resposta como 1/924 = aproximadamente 0,001082251082251082.
Aqui está a integral para cinco combinações diferentes de números duplos. O motivo do 6 é que existem 6 combinações possíveis de números duplos que não foram formadas:
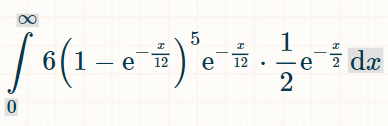
Eis a probabilidade de ganhar dentro de x unidades de tempo:
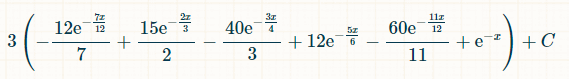
Considerando os limites de integração de 0 ao infinito, a probabilidade de rolar exatamente cinco pares distintos é 1/154.
Aqui está a integral para quatro combinações diferentes de números duplos. O motivo do 15 é que existem 6!/(4!*2!) = 15 combinações possíveis de 4 dos 6 números duplos que foram feitos:
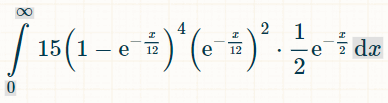
Eis a probabilidade de ganhar dentro de x unidades de tempo:
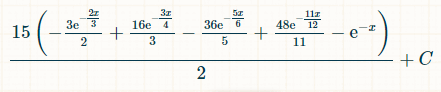
Considerando os limites de integração de 0 ao infinito, a probabilidade de rolar exatamente quatro pares distintos é 1/44.
Aqui está a integral para três números duplos distintos. O motivo do 20 é que existem 6!/(3!*3!) = 20 combinações possíveis de 3 dos 6 números duplos que foram formados:
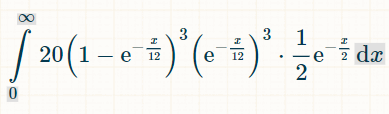
Eis a probabilidade de ganhar dentro de x unidades de tempo:
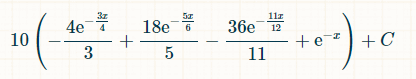
Considerando os limites de integração de 0 ao infinito, a probabilidade de rolar exatamente três pares distintos é 2/33.



