Nesta página
Aposta de fogo
Introdução
A aposta Fire Bet é uma aposta paralela popular no craps que paga com base no número de pontos únicos estabelecidos e ganhos pelo lançador. Conheço três tabelas de pagamento, conforme descrito a seguir. A vantagem da casa em cada uma delas está na última linha da tabela. A Tabela de Pagamento 1 é a mais comum. Os pagamentos são indicados em uma base de "para um". Um valor negativo indica uma perda.
Tabelas de Pagamento de Apostas de Fogo
| Pontos abordados | Tabela de Pagamento A | Tabela de Pagamento B | Tabela de Pagamento C |
|---|---|---|---|
| 6 | 999 | 2000 | 299 |
| 5 | 249 | 200 | 149 |
| 4 | 24 | 10 | 29 |
| 3 | -1 | -1 | 6 |
| 2 | -1 | -1 | -1 |
| 1 | -1 | -1 | -1 |
| 0 | -1 | -1 | -1 |
| Borda da casa | 20,76% | 24,86% | 20,73% |
A seguir, apresento minha análise da Tabela de Pagamentos A. A célula inferior direita mostra uma vantagem da casa de 20,76%.
Aposta de Fogo — Tabela de Pagamentos A
| Pontos abordados | Paga | Probabilidade | Retornar |
|---|---|---|---|
| 0 | -1 | 0,593939 | -0,593939 |
| 1 | -1 | 0,260750 | -0,26075 |
| 2 | -1 | 0,101275 | -0,101275 |
| 3 | -1 | 0,033434 | -0,033434 |
| 4 | 24 | 0,008798 | 0,211156 |
| 5 | 249 | 0,001640 | 0,408343 |
| 6 | 999 | 0,000162 | 0,162272 |
| Total | 1 | -0,207628 |
A seguir, apresento minha análise da Tabela de Pagamentos B. A célula inferior direita mostra uma vantagem da casa de 24,86%.
Aposta de Fogo — Tabela de Pagamentos B
| Pontos abordados | Paga | Probabilidade | Retornar |
|---|---|---|---|
| 0 | -1 | 0,593939 | -0,593939 |
| 1 | -1 | 0,260750 | -0,26075 |
| 2 | -1 | 0,101275 | -0,101275 |
| 3 | -1 | 0,033434 | -0,033434 |
| 4 | 10 | 0,008798 | 0,087982 |
| 5 | 200 | 0,001640 | 0,327987 |
| 6 | 2000 | 0,000162 | 0,324869 |
| Total | 1 | -0,248562 |
A seguir, apresento minha análise da Tabela de Pagamentos C. A célula inferior direita mostra uma vantagem da casa de 20,73%.
Aposta de Fogo — Tabela de Pagamentos C
| Pontos abordados | Paga | Probabilidade | Retornar |
|---|---|---|---|
| 0 | -1 | 0,593939 | -0,593939 |
| 1 | -1 | 0,260750 | -0,26075 |
| 2 | -1 | 0,101275 | -0,101275 |
| 3 | 6 | 0,033434 | 0,200605 |
| 4 | 29 | 0,008798 | 0,255147 |
| 5 | 149 | 0,001640 | 0,244350 |
| 6 | 299 | 0,000162 | 0,048568 |
| Total | 1 | -0,207295 |
A tabela a seguir mostra as probabilidades de se obter de 0 a 6 pontos, com o máximo de dígitos significativos que o Excel suporta.
Probabilidades de apostas de fogo
| Pontos abordados | Probabilidade |
|---|---|
| 0 | 0,593939393939394 |
| 1 | 0,260750492003903 |
| 2 | 0,101275355549231 |
| 3 | 0,0334342121788456 |
| 4 | 0,00879817844040312 |
| 5 | 0,00163993313895325 |
| 6 | 0,000162434749269826 |
Frequentemente me perguntam como calcular as probabilidades acima. É um problema matemático complexo. Abaixo, listo três maneiras de calcular a probabilidade de se obter qualquer número de pontos, de 0 a 6.
Simulação aleatória
Uma simulação aleatória é a maneira mais fácil de analisar a Fire Bet. Com a velocidade dos computadores modernos, ela também é extremamente precisa. Apenas os puristas matemáticos mais rigorosos (como eu) se esforçarão para obter uma solução exata. A tabela a seguir mostra os resultados de uma simulação de quase 40 bilhões de apostas Fire resolvidas contra a tabela de pagamentos A. A célula inferior direita mostra uma vantagem da casa de 20,7531%. A vantagem real da casa é de 20,7628%, portanto, a simulação teve uma precisão de 0,01% de retorno.
Simulação de aposta de fogo
| Pontos abordados | Paga | Vitórias | Probabilidade | Retornar |
|---|---|---|---|---|
| 6 | 999 | 6.452.452 | 0,000162 | 0,162257 |
| 5 | 249 | 65.165.019 | 0,001640 | 0,408438 |
| 4 | 24 | 349.553.690 | 0,008799 | 0,211173 |
| 3 | -1 | 1.328.267.592 | 0,033435 | -0,033435 |
| 2 | -1 | 4.023.371.732 | 0,101275 | -0,101275 |
| 1 | -1 | 10.358.742.102 | 0,260747 | -0,260747 |
| 0 | -1 | 23.595.605.529 | 0,593941 | -0,593941 |
| Total | 39.727.158.116 | 1.000000 | -0,207531 |
Cadeia de Markov
Uma maneira de calcular com precisão as probabilidades da Aposta de Fogo é usando uma Cadeia de Markov. Isso significa calcular a probabilidade de completar qualquer número futuro de pontos, dado qualquer um dos 64 estados possíveis de pontos já obtidos. O cálculo é relativamente simples no final, precisando apenas de mais um ponto para completar os seis. Em seguida, o processo retorna ao estado inicial da primeira rodada.
Este primeiro estado é representado pela primeira linha da tabela, sem contar os cabeçalhos das colunas. Ele mostra as probabilidades apresentadas acima para completar qualquer número de pontos de 0 a 6.
Cadeia de Markov de aposta de fogo
| Pontos Já Feito | Probabilidade 0 pontos | Probabilidade 1 ponto | Probabilidade 2 pontos | Probabilidade 3 pontos | Probabilidade 4 pontos | Probabilidade 5 pontos | Probabilidade 6 pontos |
|---|---|---|---|---|---|---|---|
| Nenhum | 0,593939 | 0,260750 | 0,101275 | 0,033434 | 0,008798 | 0,001640 | 0,000162 |
| 10 | 0,000000 | 0,619763 | 0,256759 | 0,091331 | 0,026183 | 0,005375 | 0,000589 |
| 9 | 0,000000 | 0,636364 | 0,252138 | 0,084540 | 0,022402 | 0,004153 | 0,000404 |
| 9,10 | 0,000000 | 0,000000 | 0,666100 | 0,244772 | 0,072316 | 0,015152 | 0,001660 |
| 8 | 0,000000 | 0,656067 | 0,244255 | 0,076831 | 0,019163 | 0,003370 | 0,000314 |
| 8,10 | 0,000000 | 0,000000 | 0,687719 | 0,234612 | 0,063990 | 0,012405 | 0,001274 |
| 8,9 | 0,000000 | 0,000000 | 0,708220 | 0,225365 | 0,055933 | 0,009618 | 0,000864 |
| 8,9,10 | 0,000000 | 0,000000 | 0,000000 | 0,745247 | 0,209635 | 0,041004 | 0,004114 |
| 6 | 0,000000 | 0,656067 | 0,244255 | 0,076831 | 0,019163 | 0,003370 | 0,000314 |
| 6,10 | 0,000000 | 0,000000 | 0,687719 | 0,234612 | 0,063990 | 0,012405 | 0,001274 |
| 6,9 | 0,000000 | 0,000000 | 0,708220 | 0,225365 | 0,055933 | 0,009618 | 0,000864 |
| 6,9,10 | 0,000000 | 0,000000 | 0,000000 | 0,745247 | 0,209635 | 0,041004 | 0,004114 |
| 6,8 | 0,000000 | 0,000000 | 0,732710 | 0,210728 | 0,048135 | 0,007762 | 0,000665 |
| 6,8,10 | 0,000000 | 0,000000 | 0,000000 | 0,772414 | 0,190903 | 0,033563 | 0,003120 |
| 6,8,9 | 0,000000 | 0,000000 | 0,000000 | 0,798371 | 0,173323 | 0,026215 | 0,002091 |
| 6,8,9,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,845739 | 0,142050 | 0,012211 |
| 5 | 0,000000 | 0,636364 | 0,252138 | 0,084540 | 0.022402 | 0,004153 | 0,000404 |
| 5,10 | 0,000000 | 0,000000 | 0,666100 | 0,244772 | 0,072316 | 0,015152 | 0,001660 |
| 5,9 | 0,000000 | 0,000000 | 0,685315 | 0,237358 | 0,064328 | 0,011875 | 0,001124 |
| 5,9,10 | 0,000000 | 0,000000 | 0,000000 | 0,719927 | 0,224997 | 0,049645 | 0,005432 |
| 5,8 | 0,000000 | 0,000000 | 0,708220 | 0,225365 | 0,055933 | 0,009618 | 0,000864 |
| 5,8,10 | 0,000000 | 0,000000 | 0,000000 | 0,745247 | 0,209635 | 0,041004 | 0,004114 |
| 5,8,9 | 0,000000 | 0,000000 | 0,000000 | 0,769382 | 0,195368 | 0,032496 | 0,002754 |
| 5,8,9,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,813278 | 0,170376 | 0,016346 |
| 5,6 | 0,000000 | 0,000000 | 0,708220 | 0,225365 | 0,055933 | 0,009618 | 0,000864 |
| 5,6,10 | 0,000000 | 0,000000 | 0,000000 | 0,745247 | 0,209635 | 0,041004 | 0,004114 |
| 5,6,9 | 0,000000 | 0,000000 | 0,000000 | 0,769382 | 0,195368 | 0,032496 | 0,002754 |
| 5,6,9,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,813278 | 0,170376 | 0,016346 |
| 5,6,8 | 0,000000 | 0,000000 | 0,000000 | 0,798371 | 0,173323 | 0,026215 | 0,002091 |
| 5,6,8,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,845739 | 0,142050 | 0,012211 |
| 5,6,8,9 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,876957 | 0,114977 | 0,008066 |
| 5,6,8,9,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,934446 | 0,065554 |
| 4 | 0,000000 | 0,619763 | 0,256759 | 0,091331 | 0,026183 | 0,005375 | 0,000589 |
| 4,10 | 0,000000 | 0,000000 | 0,647934 | 0,250930 | 0,079930 | 0,018752 | 0,002454 |
| 4,9 | 0,000000 | 0,000000 | 0,666100 | 0,244772 | 0,072316 | 0,015152 | 0,001660 |
| 4,9,10 | 0,000000 | 0,000000 | 0,000000 | 0,698752 | 0,234682 | 0,058434 | 0,008131 |
| 4,8 | 0,000000 | 0,000000 | 0,687719 | 0,234612 | 0,063990 | 0,012405 | 0,001274 |
| 4,8,10 | 0,000000 | 0,000000 | 0,000000 | 0,722581 | 0,221643 | 0,049624 | 0,006153 |
| 4,8,9 | 0,000000 | 0,000000 | 0,000000 | 0,745247 | 0,209635 | 0,041004 | 0,004114 |
| 4,8,9,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,786359 | 0.188851 | 0,024790 |
| 4,6 | 0,000000 | 0,000000 | 0,687719 | 0,234612 | 0,063990 | 0,012405 | 0,001274 |
| 4,6,10 | 0,000000 | 0,000000 | 0,000000 | 0,722581 | 0,221643 | 0,049624 | 0,006153 |
| 4,6,9 | 0,000000 | 0,000000 | 0,000000 | 0,745247 | 0,209635 | 0,041004 | 0,004114 |
| 4,6,9,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,786359 | 0,188851 | 0,024790 |
| 4,6,8 | 0,000000 | 0,000000 | 0,000000 | 0,772414 | 0,190903 | 0,033563 | 0,003120 |
| 4,6,8,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,816667 | 0,164832 | 0,018502 |
| 4,6,8,9 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,845739 | 0,142050 | 0,012211 |
| 4,6,8,9,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,899083 | 0,100917 |
| 4,5 | 0,000000 | 0,000000 | 0,666100 | 0,244772 | 0,072316 | 0,015152 | 0,001660 |
| 4,5,10 | 0,000000 | 0,000000 | 0,000000 | 0,698752 | 0,234682 | 0,058434 | 0,008131 |
| 4,5,9 | 0,000000 | 0,000000 | 0,000000 | 0,719927 | 0,224997 | 0,049645 | 0,005432 |
| 4,5,9,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,758221 | 0,208531 | 0,033248 |
| 4,5,8 | 0,000000 | 0,000000 | 0,000000 | 0,745247 | 0,209635 | 0,041004 | 0,004114 |
| 4,5,8,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,786359 | 0,188851 | 0,024790 |
| 4,5,8,9 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,813278 | 0,170376 | 0,016346 |
| 4,5,8,9,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,862486 | 0,137514 |
| 4,5,6 | 0,000000 | 0,000000 | 0,000000 | 0,745247 | 0,209635 | 0,041004 | 0,004114 |
| 4,5,6,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,786359 | 0,188851 | 0,024790 |
| 4,5,6,9 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,813278 | 0,170376 | 0,016346 |
| 4,5,6,9,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,862486 | 0,137514 |
| 4,5,6,8 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,845739 | 0,142050 | 0,012211 |
| 4,5,6,8,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,899083 | 0,100917 |
| 4,5,6,8,9 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0.934446 | 0,065554 |
| 4,5,6,8,9,10 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 1.000000 |
Se você pretende tentar recriar meu trabalho, aqui vão algumas dicas sobre como ir de um estado para outro. Comece pelos estados próximos ao final, nos quais o atirador já fez 5 pontos. Por exemplo, se o atirador precisa apenas de 4 pontos, três coisas podem acontecer: (1) Ele estabelece e acerta os 4 pontos, (2) Ele estabelece e acerta um ponto que já havia feito, (3) Ele erra o alvo. A probabilidade de (1) é (3/24)*(1/3) = 1/24 = 0,041667. A probabilidade de (2) é (4/24)*(2/5) + (5/24)*(5/11) + (5/24)*(5/11) + (4/24)*(2/5) + (3/24)*(1/3) = 0,364394. A probabilidade de (3) é 1 - 0,041667 - 0,364394 = 0,593939. Eventualmente, o evento (1) ou (3) ocorrerá. A probabilidade de (1) ocorrer antes de (3) é 0,041667/(0,041667 + 0,593939) = 0,065554. Recorra recursivamente ao ponto de partida. Isso pode ser demorado, redundante e tedioso, ou você pode automatizar o processo em uma planilha.
Cálculo
O primeiro passo neste método é calcular a probabilidade de todos os 7 resultados possíveis relevantes de uma aposta na linha de passe após o estabelecimento de um ponto. Podemos ignorar as 12 combinações, ou 1/3 de chance, de o jogador ganhar ou perder imediatamente na primeira jogada, porque esses eventos não são significativos para a Aposta de Fogo. Portanto, a primeira jogada é baseada em 24 combinações possíveis, em vez de 36.
- Ponto de 4 feito e ganho = (3/24) × (3/9) = 1/24 = aproximadamente 4,17%
- Ponto de 5 feito e ganho = (4/24) × (4/10) = 1/15 = aproximadamente 6,67%
- Ponto de 6 feito e ganho = (5/24) × (5/11) = 25/264 = aproximadamente 9,47%
- Ponto de 8 feito e ganho = (5/24) × (5/11) = 25/264 = aproximadamente 9,47%
- Ponto de 9 feito e ganho = (4/24) × (4/10) = 1/15 = aproximadamente 6,67%
- Ponto de 10 feito e ganho = (3/24) × (3/9) = 1/24 = aproximadamente 4,17%
- Qualquer ponto marcado e 7-out = 2×((3/24) × (6/9))+ 2× ((4/24) × (6/10)) + 2×((5/24) × (6/11)) = 98/165 = aproximadamente 59,39%
Observe que a soma dessas probabilidades é igual a 1.
Em seguida, em vez de a Aposta de Fogo ser decidida pelo lançamento de dois dados, um de cada vez, considere que o tempo entre os eventos ocorre aleatoriamente, seguindo uma distribuição exponencial com média de uma unidade de tempo entre os eventos. Se um evento ocorrer, ele seguirá as probabilidades do craps que acabamos de calcular.
Por exemplo, a probabilidade de uma vitória de 0,4 é 1/24. Assim, o tempo entre vitórias de 0,4 será em média de 24 unidades. A probabilidade de passar x unidades de tempo sem uma vitória de 0,10 é exp(-x/24). Complementando, a probabilidade de pelo menos uma vitória de 0,10 em x unidades de tempo é 1-exp(-x/24).
Para determinar o resultado da Aposta do Fogo, não importa quanto tempo decorra entre os eventos, apenas quais são os eventos. Portanto, podemos integrar o tempo total até que um vencedor da aposta ganhe da seguinte forma:
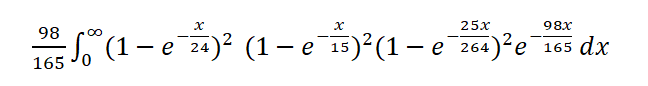
Deixe-me explicar o que essa integral significa. Ela representa a probabilidade de que, após x unidades de tempo, tenha havido pelo menos uma vitória para cada ponto, exceto para o 7. Como a probabilidade de uma vitória com 0,4 e 0,10 é a mesma, podemos elevar ao quadrado a probabilidade de uma vitória com 0,4. O mesmo vale para 5 e 9, assim como para 6 e 8. Finalmente, multiplicamos tudo por 98/165, a probabilidade de um 7, para fechar a aposta. Se não fizéssemos isso, o jogador poderia receber pagamento por múltiplas vitórias sobrepostas.
Integrar isso manualmente seria muito trabalhoso e propenso a erros. Felizmente, existem calculadoras de integrais . Para usar uma para este problema, clique no link e insira o seguinte na caixa de texto na parte superior: (1-exp(-x/24))^2*(1-exp(-x/15))^2*(1-exp(-25x/264))^2*exp(-98x/165)/(165/98). Em seguida, clique em "Opções" e defina o limite inferior como 0 e o limite superior como infinito. Depois, clique em "Executar".
Antes de considerar os limites de integração, a resposta é (98*(-(165*e^(-(98*x)/165))/98+(2640*e^(-(839*x)/1320))/839+(330*e^(-(109*x)/165))/109-(220*e^(-(149*x)/220))/149+(880*e^(-(303*x)/440))/303-(1760*e^(-(309*x)/440))/309-(11* e^(-(8*x)/11))/8-(1320*e^(-(241*x)/330))/241+(1320*e^(-(491*x)/660))/491-(5280*e^(-(99 7*x)/1320))/997+(528*e^(-(203*x)/264))/203+(2640*e^(-(1019*x)/1320))/1019-(60*e^(-(47*x )/60))/47+(2640*e^(-(263*x)/330))/263-(132*e^(-(107*x)/132))/107+(528*e^(-(217*x)/264) )/217+(80*e^(-(33*x)/40))/33-(1760*e^(-(369*x)/440))/369+(40*e^(-(17*x)/20))/17-(88*e^( -(19*x)/22))/19-(15*e^(-(13*x)/15))/13-(480*e^(-(107*x)/120))/107+(528*e^(-(239*x)/264) )/239-(12*e^(-(11*x)/12))/11+(15*e^(-(14*x)/15))/7+(48*e^(-(23*x)/24))/23-e^(-x)))/165.
Felizmente, essa calculadora permite limites de integração e fornece a solução como 3700403899126040038831518494284887738125 / 22780863797678919004236184338193605974839452, que é aproximadamente igual a 0,0001624347492698264.
Claro, essa é apenas a probabilidade de acertar todos os seis pontos, mas a mesma lógica poderia ser usada para encontrar a probabilidade de qualquer número de pontos. Deixo isso como um exercício para o leitor ;-).
Links externos
- A matemática das apostas Fire Bet é discutida no meu site complementar, Wizard of Vegas.
- Veja a minha planilha , que publiquei no Google Docs para quem quiser baixar.
- O livro "A Doutrina das Probabilidades: Aspectos Probabilísticos do Jogo" de Stewart N. Ethier aborda a matemática das apostas Fire Bet.
Agradecimentos
Gostaria de agradecer ao membro Ace2 do fórum Wizard of Vegas por seus incansáveis conselhos sobre como calcular a probabilidade da Aposta de Fogo usando integração.



