Nesta página
Oponente de pôquer
Introdução
Opponent Poker é uma variação de video poker que observei no Red Rock Resort em 17 de dezembro de 2006. A primeira aposta de cinco créditos funciona como no video poker tradicional, e os cinco créditos seguintes são somados aos de dois oponentes controlados pelo computador, sendo que a melhor mão de video poker leva tudo.
Regras
- O jogador pode apostar 0, 1, 2, 3, 4, 5 ou 10 créditos.
- Se o jogador apostar 5 créditos ou menos, o jogo funcionará como um vídeo pôquer comum.
- Se o jogador apostar dez créditos, cinco deles funcionarão como uma aposta normal de video poker. Os outros cinco créditos serão usados para jogar contra dois oponentes controlados pelo computador.
- Supondo que dez créditos sejam apostados, após a distribuição das cinco cartas iniciais, ambos os oponentes controlados pelo computador indicarão quais cartas manterão. De acordo com as regras do jogo, a estratégia do oponente é "uma estratégia padrão de pôquer". Eu não conheço essa estratégia, mas, com base na minha experiência jogando Opponent Poker, geralmente, embora nem sempre, é a estratégia ideal para videopôquer.
- O jogador escolherá quais cartas deseja manter.
- O jogador e ambos os oponentes receberão cartas de reposição do mesmo baralho de 52 cartas.
- Se o jogador tiver uma mão de video poker com um pagamento maior do que os outros dois oponentes controlados pelo computador, ele ganhará os ganhos do video poker das três mãos.
- Caso dois ou três participantes empatem na mão de video poker com o maior prêmio, o pote de ganhos combinados do video poker será transferido para a próxima mão.
- Em caso de empate entre as mãos, o jogador pode optar por dividir o pote. Os potes divididos serão arredondados para baixo, para o crédito mais próximo.
- O pote será dividido automaticamente se houver um royal flush, se o jogador desistir da partida ou se o jogador trocar de jogo.
Estratégia
Não sei qual é a "estratégia padrão de pôquer" para os oponentes de computador, então não posso quantificar uma estratégia ideal para o jogador. Acredito que, se o jogador seguisse a estratégia ideal de vídeo pôquer para a tabela de pagamentos em questão, seu retorno seria maior do que o do vídeo pôquer convencional. O jogador não deve jogar sempre da mesma forma que os oponentes de computador. Por exemplo, a mão inicial era K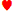 UM
UM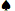 Q
Q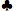 8
8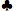 9
9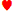 Ambos os oponentes virtuais tinham dama, rei e ás. A estratégia ideal no vídeo pôquer é ter apenas o rei e a dama. Ter as mesmas cartas que os oponentes virtuais sempre resulta no mesmo valor esperado que no vídeo pôquer convencional. Neste caso, ter as três cartas altas tem um valor esperado de 4,560592 créditos (2,280296 créditos para a aposta do vídeo pôquer e para a aposta do oponente). Ter apenas a dama e o rei tem um valor esperado de 4,863301 créditos (2,397471 para a mão do vídeo pôquer e 2,46583 para a aposta do oponente). Isso demonstra que (1) os oponentes nem sempre seguem a estratégia ideal no vídeo pôquer e (2) você não deve jogar sempre da mesma forma que os oponentes.
Ambos os oponentes virtuais tinham dama, rei e ás. A estratégia ideal no vídeo pôquer é ter apenas o rei e a dama. Ter as mesmas cartas que os oponentes virtuais sempre resulta no mesmo valor esperado que no vídeo pôquer convencional. Neste caso, ter as três cartas altas tem um valor esperado de 4,560592 créditos (2,280296 créditos para a aposta do vídeo pôquer e para a aposta do oponente). Ter apenas a dama e o rei tem um valor esperado de 4,863301 créditos (2,397471 para a mão do vídeo pôquer e 2,46583 para a aposta do oponente). Isso demonstra que (1) os oponentes nem sempre seguem a estratégia ideal no vídeo pôquer e (2) você não deve jogar sempre da mesma forma que os oponentes.
Retornar
Conforme mencionado na seção de estratégia, desconheço a "estratégia padrão de pôquer" e, portanto, não posso quantificar nem uma estratégia perfeita nem o retorno máximo. Tudo o que posso fazer é indicar as tabelas de retorno das mesas de videopôquer observadas no Red Rock Resort. Acredito que o retorno máximo seja ligeiramente superior aos retornos abaixo.
"9/5" Jacks ou Melhor
| Mão | Pague | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| Rubor Real | 800 | 496237776 | 0,000025 | 0,019916 |
| Straight flush | 50 | 2137447980 | 0,000107 | 0,005362 |
| 4 de um tipo | 25 | 47100799404 | 0,002363 | 0,059073 |
| Casa cheia | 9 | 229510637676 | 0,011514 | 0,103626 |
| Descarga | 5 | 217120426644 | 0,010892 | 0.054462 |
| Direto | 4 | 223861063908 | 0,011231 | 0,044922 |
| 3 de um tipo | 3 | 1484332642620 | 0,074465 | 0,223396 |
| Dois pares | 2 | 2577431192796 | 0,129303 | 0,258606 |
| Valetes ou melhor | 1 | 4288342040640 | 0,215135 | 0,215135 |
| Nada | 0 | 10862898027756 | 0,544964 | 0,000000 |
| Total | 0 | 1.000000 | 0,984498 |
Bônus "8/5" Poker Deluxe
| Mão | Pague | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| Rubor Real | 800 | 491855652 | 0,000025 | 0,019740 |
| Straight flush | 50 | 2154130740 | 0,000108 | 0,005403 |
| 4 de um tipo | 80 | 47005788324 | 0,002358 | 0,188653 |
| Casa cheia | 8 | 228890564676 | 0,011483 | 0,091863 |
| Descarga | 5 | 216493699248 | 0,010861 | 0,054305 |
| Direto | 4 | 260258167080 | 0,013056 | 0,052226 |
| 3 de um tipo | 3 | 1475243948064 | 0,074009 | 0,222028 |
| Dois pares | 1 | 2556435840408 | 0,128250 | 0,128250 |
| Valetes ou melhor | 1 | 4216703051664 | 0,211541 | 0,211541 |
| Nada | 0 | 10929553471344 | 0,548308 | 0,000000 |
| Total | 19933230517200 | 1.000000 | 0,974009 |
Bônus Duplo "9/5" — 97,87%
| Mão | Pague | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| Rubor Real | 800 | 497516688 | 0,000025 | 0,019967 |
| Straight flush | 50 | 2123092824 | 0,000107 | 0,005326 |
| 4 ases + 2-4 | 400 | 1228310184 | 0,000062 | 0,024648 |
| 4 2-4 + A-4 | 160 | 2854473252 | 0,000143 | 0,022912 |
| 4 ases + 5-K | 160 | 3459809880 | 0,000174 | 0,027771 |
| 4 2-4 + 5-K | 80 | 7662852888 | 0,000384 | 0,030754 |
| 4 5-K | 50 | 32536223652 | 0,001632 | 0,081613 |
| Casa cheia | 9 | 216639836640 | 0,010868 | 0,097814 |
| Descarga | 5 | 218785162368 | 0,010976 | 0,054880 |
| Direto | 4 | 257980198392 | 0,012942 | 0,051769 |
| 3 de um tipo | 3 | 1501776975600 | 0,075340 | 0,226021 |
| Dois pares | 1 | 2454744788496 | 0,123148 | 0,123148 |
| Valetes ou melhor | 1 | 4227940545588 | 0,212105 | 0,212105 |
| Nada | 0 | 11005000730748 | 0,552093 | 0,000000 |
| Total | 0 | 19933230517200 | 1.000000 | 0,978729 |
Deuces Wild — 97,58%
| Mão | Pague | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| sequência real natural | 800 | 452258388 | 0,000023 | 0,018151 |
| Quatro dois | 200 | 3681116136 | 0,000185 | 0,036934 |
| sequência real selvagem | 20 | 35519655168 | 0,001782 | 0,035639 |
| Cinco de um tipo | 12 | 59450103984 | 0,002982 | 0,035790 |
| Straight flush | 10 | 109163645748 | 0,005476 | 0,054765 |
| Quatro de um mesmo tipo | 4 | 1213460173776 | 0,060876 | 0,243505 |
| Casa cheia | 4 | 520454143512 | 0,026110 | 0,104439 |
| Descarga | 3 | 420473233680 | 0,021094 | 0,063282 |
| Direto | 2 | 1160573109144 | 0,058223 | 0,116446 |
| Três de um tipo | 1 | 5318990094612 | 0,266840 | 0,266840 |
| Nada | 0 | 11091012983052 | 0,556408 | 0,000000 |
| Total | 0 | 19933230517200 | 1.000000 | 0,975791 |
Um aspecto interessante deste jogo é que, de acordo com as regras, o prêmio acumulado pode crescer infinitamente. Isso não parece infringir a regulamentação 14.2.070 do Conselho de Controle de Jogos de Nevada, que estipula que, se a probabilidade de ganhar o prêmio máximo for inferior a 1 em 100 milhões, essa probabilidade deve ser exibida de forma destacada. Em qualquer mão, o prêmio máximo é o valor acumulado mais 8.000 créditos, para um Royal Flush, e essa probabilidade é de 1 em 649.740.


