Nesta página
Corra contra o Ás
Introdução
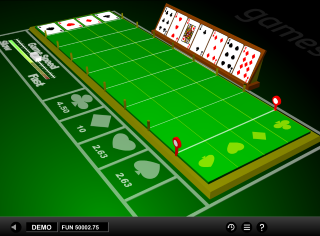
Race the Ace é um jogo de corrida simples no estilo Derby, desenvolvido pela 1x2 Gaming . A ideia é que o jogador aposte em um naipe. Em seguida, cartas aleatórias são sorteadas de um baralho até que um naipe apareça oito vezes, momento em que esse naipe se torna o vencedor. O jogador pode apostar antes ou depois de receber as sete cartas iniciais.
Os retornos variam de 50,71% a 97,26%, dependendo da aposta que você fizer, então escolha seu traje com cuidado.
Regras
- O jogo é jogado com um baralho de 48 cartas, usando todas as cartas exceto os ases.
- Os quatro ases removidos serão colocados na linha de partida de um campo.
- O jogador pode apostar "Ante Post" ou "With Form".
- Se o jogador escolher "Ante Post", ele apostará neste momento em um dos quatro naipes. Cada aposta pagará 3,75 para 1 se for vencedora. Após o jogador fazer uma aposta, as sete primeiras cartas do baralho serão reveladas.
- Se o jogador escolher "Com Forma", as sete primeiras cartas do baralho serão reveladas. As probabilidades serão então ajustadas de acordo com quantas cartas de cada naipe forem removidas. O jogador poderá então apostar em qualquer naipe.
- O jogo parece eliminar situações em que cinco ou mais cartas de um determinado naipe são removidas, porque então seria impossível para esse naipe vencer, já que não haveria cartas suficientes desse naipe para chegar à linha de chegada.
- Em seguida, a corrida começará com as 41 cartas restantes, que serão reveladas uma de cada vez.
- À medida que cada carta é revelada, o ás do naipe daquela carta avança uma posição.
- O primeiro ás a avançar oito vezes vence, e as apostas no naipe desse ás também vencem.
Se o jogador escolher apostar "Com Forma", as sete primeiras cartas do baralho são reveladas antes da corrida. Obviamente, isso altera as probabilidades. Quanto mais cartas de um determinado naipe forem removidas do baralho, menores serão as chances de esse naipe vencer e, consequentemente, maior será o pagamento da aposta vencedora. Percebi que cinco ou mais cartas do mesmo naipe nunca são removidas, pois isso resultaria em zero chance de vitória. Restam, portanto, sete outras maneiras de distribuir os naipes nas sete primeiras cartas. A tabela a seguir mostra essas sete maneiras de remover sete naipes e as probabilidades de pagamento de cada naipe. Todas as vitórias são "para um", ou seja, o jogador não recebe sua aposta original de volta em caso de vitória.
Tabela de Pagamento da Corrida Ace
| Terno 1 Removido | Terno 2 Removido | Terno 3 Removido | Terno 4 Removido | Terno 1 Paga | Terno 2 Paga | Terno 3 Paga | Terno 4 Paga |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 4 | 2.05 | 2.05 | 11 | 34 |
| 0 | 1 | 2 | 4 | 1,83 | 3 | 5,5 | 34 |
| 0 | 1 | 3 | 3 | 1.8 | 2,87 | 11 | 11 |
| 0 | 2 | 2 | 3 | 1,61 | 5.2 | 5.2 | 12 |
| 1 | 2 | 2 | 2 | 2,5 | 4,33 | 4,33 | 4,33 |
| 1 | 1 | 2 | 3 | 2,63 | 2,63 | 4,5 | 10 |
| 1 | 1 | 1 | 4 | 2,87 | 2,87 | 2,87 | 26 |
Vejamos este exemplo. Nas primeiras sete cartas no tabuleiro, ao longo da trilha, há um espadas, um copas, três ouros e dois paus. Isso segue o padrão "1-1-2-3" de distribuição de naipes na tabela acima. Portanto, ambos os naipes com uma carta removida (espadas e copas) pagam 2,63, o com duas cartas removidas (paus) paga 4,5 e o com três cartas removidas (ouros) paga 10.
Análise
Quando o jogador joga Ante Post, ou seja, antes de ver as primeiras sete cartas, sua probabilidade de ganhar é obviamente de 25%. Com odds de 3,75 para 1, o retorno esperado é de 93,75%.
A tabela a seguir mostra a probabilidade de ganhar, as chances de vitória e o retorno esperado quando as sete cartas iniciais seguem a distribuição de naipe 0-0-3-4. Observe que as melhores chances são obtidas quando um naipe não possui nenhuma carta com valor zero, com um pagamento de 2,05 e um retorno de 94,17%.
Distribuição de ternos 0-0-3-4
| Removido do terno | Paga | Probabilidade Ganhar | Esperado Retornar |
|---|---|---|---|
| 0 | 2.05 | 0,459382 | 0,941733 |
| 0 | 2.05 | 0,459382 | 0,941733 |
| 3 | 11:00 | 0,064797 | 0,712767 |
| 4 | 34,00 | 0,016440 | 0,558960 |
A tabela a seguir mostra a probabilidade de ganhar, as chances de vitória e o retorno esperado quando as sete cartas iniciais seguem a distribuição de naipe 0-1-2-4. Observe que as melhores chances ocorrem quando um naipe tem uma carta faltando, com um pagamento de 3 e um retorno de 93,68%.
Distribuição de ternos 0-1-2-4
| Removido do terno | Paga | Probabilidade Ganhar | Esperado Retornar |
|---|---|---|---|
| 0 | 1,83 | 0,500181 | 0,915331 |
| 1 | 3,00 | 0,312262 | 0,936786 |
| 2 | 5,50 | 0,169121 | 0,930166 |
| 4 | 34,00 | 0,018435 | 0,626790 |
A tabela a seguir mostra a probabilidade de ganhar, as chances de vitória e o retorno esperado quando as sete cartas iniciais seguem a distribuição de naipe 0-1-3-3. Observe que as melhores chances ocorrem quando um naipe não possui nenhuma carta faltando, com um pagamento de 1,8 e um retorno de 93,86%.
Distribuição de ternos 0-1-3-3
| Removido do terno | Paga | Probabilidade Ganhar | Esperado Retornar |
|---|---|---|---|
| 0 | 1,80 | 0,521466 | 0,938639 |
| 1 | 2,87 | 0,326610 | 0,937371 |
| 3 | 11:00 | 0,075962 | 0,835582 |
| 3 | 11:00 | 0,075962 | 0,835582 |
A tabela a seguir mostra a probabilidade de ganhar, as chances de vitória e o retorno esperado quando as sete cartas iniciais seguem a distribuição de naipe 0-2-2-3. Observe que as melhores chances ocorrem quando um naipe tem duas cartas faltando, com um pagamento de 5,2 e um retorno de 97,26%.
Distribuição de ternos 0-2-2-3
| Removido do terno | Paga | Probabilidade Ganhar | Esperado Retornar |
|---|---|---|---|
| 0 | 1,61 | 0,545564 | 0,878358 |
| 2 | 5.20 | 0,187042 | 0,972618 |
| 2 | 5.20 | 0,187042 | 0,972618 |
| 3 | 12:00 | 0,080351 | 0,964212 |
A tabela a seguir mostra a probabilidade de ganhar, as chances de vitória e o retorno esperado quando as sete cartas iniciais seguem a distribuição de naipe 1-2-2-2. Observe que as melhores chances ocorrem quando um naipe tem uma carta faltando, com um pagamento de 2,5 e um retorno de 94,41%.
Distribuição de ternos 1-2-2-2
| Removido do terno | Paga | Probabilidade Ganhar | Esperado Retornar |
|---|---|---|---|
| 1 | 2,50 | 0,377634 | 0,944085 |
| 2 | 4,33 | 0,207455 | 0,898280 |
| 2 | 4,33 | 0,207455 | 0,898280 |
| 2 | 4,33 | 0,207455 | 0,898280 |
A tabela a seguir mostra a probabilidade de ganhar, as chances de vitória e o retorno esperado quando as sete cartas iniciais seguem a distribuição de naipe 1-1-2-3. Observe que as melhores chances ocorrem quando um naipe tem uma carta faltando, com um pagamento de 2,63 e um retorno de 94,49%.
Distribuição de ternos 1-1-2-3
| Removido do terno | Paga | Probabilidade Ganhar | Esperado Retornar |
|---|---|---|---|
| 1 | 2,63 | 0,359279 | 0,944904 |
| 1 | 2,63 | 0,359279 | 0,944904 |
| 2 | 4,50 | 0,196660 | 0,884970 |
| 3 | 10,00 | 0,084783 | 0,847830 |
A tabela a seguir mostra a probabilidade de ganhar, as chances de vitória e o retorno esperado quando as sete cartas iniciais seguem a distribuição de naipe 1-1-1-4. Observe que as melhores chances ocorrem quando um naipe tem uma carta faltando, com um pagamento de 2,87 e um retorno de 93,80%.
Distribuição de ternos 1-1-1-4
| Removido do terno | Paga | Probabilidade Ganhar | Esperado Retornar |
|---|---|---|---|
| 1 | 2,87 | 0,326832 | 0,938008 |
| 1 | 2,87 | 0,326832 | 0,938008 |
| 1 | 2,87 | 0,326832 | 0,938008 |
| 4 | 26,00 | 0,019503 | 0,507078 |