Recomendações do Mago
-
Bônus de boas-vindas de $11000 -
Bônus de boas-vindas de 3000 $ -
BÔNUS DE ATÉ $777
Nesta página
Jogo da Velha
Introdução
Jogo da Velha é um jogo de cassino baseado no jogo real de mesmo nome. Um leitor me contou que o viu no Coushatta Casino Resort em Kinder, Louisiana. Há três apostas disponíveis: X, O e empate. Cartas marcadas com X ou O são sorteadas aleatoriamente em um tabuleiro de jogo da velha para determinar o resultado vencedor.
Regras
- O jogo utiliza quatro baralhos de 52 cartas. Cada baralho consiste em 26 cartas marcadas com X e 26 cartas marcadas com O.
- As cartas são retiradas do sapato e colocadas nos 9 quadrados do tabuleiro do jogo da velha. As cartas continuam sendo colocadas até que haja um vencedor (X ou O com três em linha), ou até que todos os quadrados do tabuleiro estejam cobertos, o que ocorrer primeiro.
- Uma aposta vencedora em X ou O paga o valor apostado. Em caso de empate, as apostas em X ou O perdem metade do valor apostado.
- Uma aposta vencedora no empate pagará 14 para 1.
Análise
A tabela a seguir mostra a probabilidade de 0 a 9 cartas com a letra X e a probabilidade de um empate, dado esse número de Xs. A primeira coluna indica o número de Xs em 9. A segunda coluna mostra a probabilidade desse número de Xs na carta. A terceira coluna mostra a probabilidade condicional de um empate, dado o número de Xs naquela linha. A quarta coluna é o produto da segunda e da terceira colunas. A célula inferior direita mostra que a probabilidade de um empate é de 6,3735%.
Probabilidade de empate no Jogo da Velha — Quatro Baralhos
| Número Xs | Probabilidade | Probabilidade condicional de um empate | Produto |
|---|---|---|---|
| 0 | 0,001631 | 0 | 0 |
| 1 | 0,015898 | 0 | 0 |
| 2 | 0,067526 | 0 | 0 |
| 3 | 0,163991 | 0 | 0 |
| 4 | 0,250955 | 0,126984 | 0,031867 |
| 5 | 0,250955 | 0,126984 | 0,031867 |
| 6 | 0,163991 | 0 | 0 |
| 7 | 0,067526 | 0 | 0 |
| 8 | 0,015898 | 0 | 0 |
| 9 | 0,001631 | 0 | 0 |
| Total | 1.000000 | 0,063735 |
Se houver 4 Xs e 5 Os, então existem combin (9,4) = 126 maneiras de colocar os Xs e Os no tabuleiro. Dessas 126, 16 resultam em um empate. A imagem abaixo mostra os três padrões de empate e o número de maneiras pelas quais cada um pode ser rotacionado ou refletido. Portanto, a probabilidade de um empate, dados 4 ou 5 Xs, é 16/126 = 12,70%.
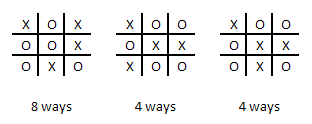
Uma vez que se aceite que a probabilidade de um empate é de 6,3735%, o resto é fácil. A probabilidade de não haver empate é 100% - 6,3735% = 93,6265%. A probabilidade de X ou O vencer é a metade desse valor, ou seja, 46,8133%.
A tabela a seguir mostra a probabilidade e a contribuição para o retorno de cada resultado das apostas X e O. A célula inferior direita mostra uma vantagem da casa de 3,19%.
Retorno de aposta X/O — Quatro baralhos
| Evento | Probabilidade | Paga | Retornar |
|---|---|---|---|
| Ganhar | 0,468133 | 1 | 0,468133 |
| Gravata | 0,063735 | -0,5 | -0,031867 |
| Perda | 0,468133 | -1 | -0,468133 |
| Total | 1.000000 | -0,031867 |
A tabela a seguir mostra a probabilidade e a contribuição para o retorno de cada resultado da aposta em empate. A célula inferior direita mostra uma vantagem da casa de 4,40%.
Retorno da aposta em empate — Quatro baralhos
| Evento | Probabilidade | Paga | Retornar |
|---|---|---|---|
| Ganhar | 0,063735 | 14 | 0,892286 |
| Perda | 0,936265 | -1 | -0,936265 |
| Total | 1.000000 | -0,043980 |
A tabela final mostra a vantagem da casa em cada aposta para 4 a 8 baralhos, assumindo que não haja outras alterações nas regras.
Margem da casa — 4 a 8 decks
| Baralhos | X/O | Gravata |
|---|---|---|
| 4 | 3,19% | 4,40% |
| 5 | 3,17% | 4,78% |
| 6 | 3,17% | 5,03% |
| 7 | 3,16% | 5,20% |
| 8 | 3,16% | 5,34% |