WOO logo

Recomendações do Mago

Quebra-cabeça retangular dobrado


Nesta newsletter, apresento um enigma matemático da edição de novembro do Boletim da Mensa.

Considere um retângulo de 1x4. Agora, dobre esse retângulo de forma que os cantos opostos se sobreponham, como neste diagrama.

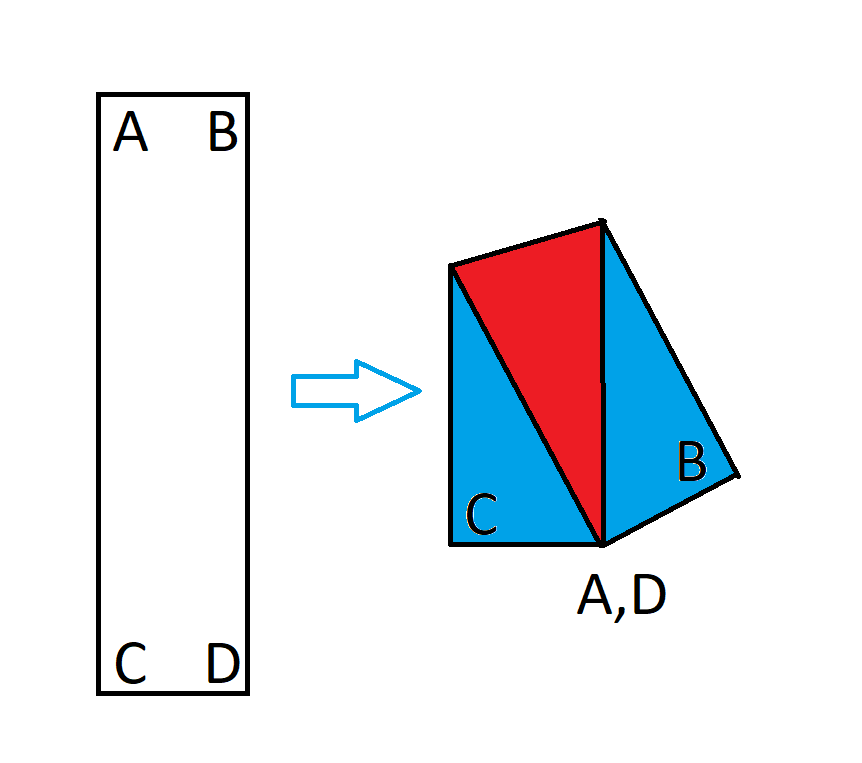
retângulo 1x4

Após a dobra do retângulo, ele forma um pentágono irregular. Qual é a razão entre a porção desse pentágono onde o papel se sobrepõe e a área total? Em outras palavras, a razão entre a área vermelha na imagem acima e a área total.

Deslize para baixo para ver a resposta e a solução.

Responder

A resposta é 17/47 = aproximadamente 0,3617

Solução

Para explicar a solução, permitam-me definir mais alguns pontos, como pode ser visto na imagem a seguir. F é o ponto médio entre E e G.

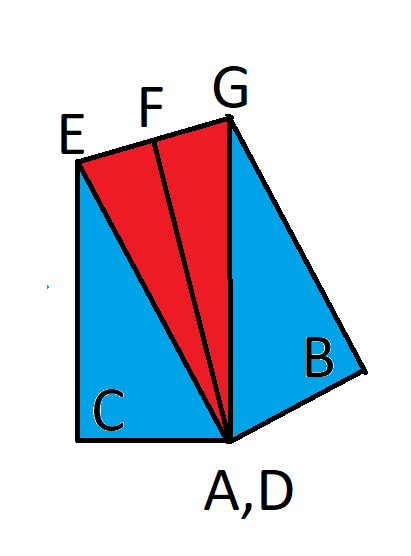
Retângulo 1x4, pentágono - solução

Nós sabemos:

AC = 1

CE + AE = 4

Vamos calcular AE usando o teorema de Pitágoras:

1 2 + (CE) 2 = (AE) 2

Substituindo 4 – CE por AE, obtemos:

1 2 + (CE) 2 = (4 – CE) 2

1 + (CE) 2 = 16 – 8 (CE) + (CE) 2

8(CE) = 15

CE = 15/8

Voltando a 1 2 + (CE) 2 = (AE) 2 , podemos resolver para (AE) já que conhecemos EC:

(AE) 2 = (CE) 2 + 1 2

(AE) 2 = (15/8) 2 + 1 2

(AE) 2 = 225/64 + 64/64

(AE) 2 = 289/64

6;font-family: 'Open Sans',sans-serif;color: #313131!important">AE = 17/8

Antes da dobra, o comprimento de A a D era a diagonal do retângulo. Usando o teorema de Pitágoras novamente, o comprimento é sqrt(17).

(AF) é metade desse comprimento, ou sqrt(17)/2.

Conhecendo AE e AF, podemos calcular EF usando o teorema de Pitágoras novamente:

(AE) 2 = (EF) 2 + (AF) 2

(17/8) 2 = (EF) 2 + (sqrt(17)/2) 2

289/64 = (EF) 2 + 17/4

289/64 = (EF) 2 + 272/64

(EF) 2 = 17/64

EF = sqrt(17)/8

Como afirmado anteriormente, F é o ponto médio de E e G. Este EG = 2*sqrt(17)/8 = sqrt(17)/4.

O triângulo vermelho, AEG = (1/2) × base × altura =

= (1/2) × quadrado (17/4) × quadrado (17)/2

= (1/2) × (17/8) = 17/16

A área do triângulo ACE = (1/2)*base*altura =

(1/2) × 1 × (15/8) = 15/16.

A área de todo o pentágono = AEG + 2*ACE =

(17/16) + 2*(15/16) = 47/16

Assim, a área da região vermelha em relação à área total do pentágono é igual a

(17/16) / (47/16) = 17/47 = aproximadamente 0,3617


Escrito por: Michael Shackleford