Demonstração de divisibilidade por 3

Esta semana, vou dar uma pausa nas curiosidades presidenciais e tentar algo novo. Sempre gostei de uma boa demonstração matemática. Até que me faltem ideias, vou analisar alguns teoremas matemáticos famosos e tentar explicar por que são verdadeiros da maneira mais simples possível. Para começar, esta semana mostrarei que se a soma dos dígitos de qualquer número inteiro for divisível por 3, então o número inteiro também será divisível por 3. No entanto, antes de chegarmos a isso, apresento o nosso habitual enigma lógico semanal.

Quebra-cabeça lógico

Há quatro cartas sobre uma mesa. Você pode ver que as cartas viradas para cima estão numeradas com D, K, 3 e 7. Você sabe que cada carta tem uma letra de um lado e um número do outro. Existe uma regra de fabricação que diz que uma carta com um D de um lado deve ter um 3 do outro. Quais duas cartas você deve virar para verificar se essa regra foi seguida?

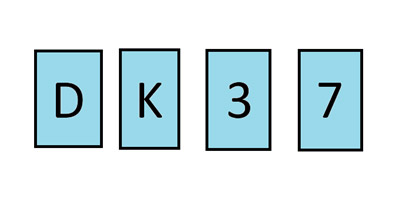
A resposta estará no final do boletim informativo.

Demonstração de divisibilidade por 3

Conforme mencionado na introdução, é possível verificar se um número inteiro é divisível por 3 da seguinte forma:

1. Some os dígitos.
2. Se a soma da regra 1 for divisível por 3, então o número original também será. Da mesma forma, se a soma não for divisível por 3, o número original também não será.

Vejamos, por exemplo, o número de telefone da Casa Branca, que é 2024567041. A soma dos dígitos é 2+0+2+4+5+6+7+0+4+1 = 31. 31 não é divisível por 3, portanto o número original também não é.

Para provar que isso funciona, decomponha o número original da seguinte forma:

6; família de fontes: 'Open Sans', sans-serif; cor: #313131 !important; ">2024567041 = (2*1000000000) + 0 + (2*10000000) + (4*1000000) + (5*100000) + (7*1000) + 0 + (4*10) + (1*1)

Em seguida, separe as potências de 10 em duas partes, um 1 e o restante do número:

= (2*(999999999+1)) + 0 + (2*(9999999+1)) + (4*(999999+1)) + (5*(99999+1)) + (7*(9999+1)) + 0 + (4*(9+1)) + (1*(0+1))

É óbvio que qualquer número composto apenas por 9 é divisível por 3. Por exemplo, 99999 = 3 * 33333.

Dito isso, vamos reorganizar os termos no número acima.

= (2*999999999) + (2*9999999) + (4*999999) + (5*99999) + (7*9999) + (4*9) + (1*0) + (2*1) + (2*1) + (4*1) + (5*1) + (7*1) + (4*1) + (1*1)

Todos os termos nos sete primeiros termos são obviamente divisíveis por 3, pois são divisíveis por um número composto apenas por 9. Em outras palavras, (2*999999999) + (2*9999999) + (4*999999) + (5*99999) + (7*9999) + (4*9) + (1*0) é divisível por 9, então podemos remover essa parte. Resta-nos:

(2*1) + (2*1) + (4*1) + (5*1) + (7*1) + (4*1) + (1*1) = 2+0+2+4+5+6+7+0+4+1 = 31

Essa é a soma dos dígitos, que é igual a 31. Como essa parte restante não é divisível por 3, o número inteiro também não pode ser dividido por 3.

Essa mesma regra também pode ser usada para verificar a divisibilidade por 9. Se a soma dos dígitos do número original for divisível por 9, então o número inteiro também será. O inverso também é verdadeiro: se a soma dos dígitos não for divisível por 9, então o número inteiro também não será.

Solução de quebra-cabeça lógico

Vamos chamar a regra que exige que o número 3 esteja no lado oposto de uma regra D de regra “D-3”.

1. • É óbvio que devemos virar a carta D para garantir que o outro lado seja um 3.
2. • O verso do cartão K deve conter um número.Já que o outro lado não pode ter um D, então esta carta não nos ajuda a refutar que a regra D-3 foi seguida.
3. • O verso da carta 3 deve conter uma letra. Se essa letra for um D, isso confirma a regra D-3. Se houver qualquer outra letra no verso, isso não nos ajuda. Portanto, ou esta carta estará de acordo com a regra D-3 ou não será relevante. De qualquer forma, estamos procurando uma carta que viole a regra para invalidá-la. Qualquer letra que esteja no verso não refutará a regra D-3. Portanto, não é necessário verificar.
4. • O verso da carta 7 deve conter uma letra. Se essa letra for um D, então essa carta refutaria a regra D-3. Portanto, é necessário verificar se não se trata de uma carta D-7, o que contradiria a afirmação D-3.

Assim, apenas as cartas D e 7 devem ser verificadas.