WOO logo

Recomendações do Mago

Identidade de Euler

Esta semana, vamos encarar um grande desafio: provar a Identidade de Euler. Caso você tenha se esquecido, ela é talvez a identidade mais bela da matemática: e ^(πi + 1) = 0. Eu gosto tanto dessa identidade que ela está no meu cartão de visitas e talvez eu até faça uma tatuagem dela. Mas antes de chegarmos a isso, apresento o nosso tradicional enigma lógico semanal.

Quebra-cabeça lógico

Você tem quatro correntes com três elos cada. Como você pode juntá-las para formar um círculo com os 12 elos, cortando apenas três deles?

Demonstrando a identidade de Euler

Uma das equações mais famosas da matemática é a Identidade de Euler, que afirma que e ^(πi) + 1 = 0. O mais incrível é que ela combina os cinco números mais importantes da matemática: 0, 1, e, π e i.

Minha solução requer o conhecimento da fórmula para uma expansão de Taylor . Para relembrar, ela é:

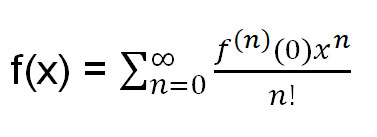
fórmula

Onde f (n) (0) = a n-ésima derivada de f(x) avaliada em 0.

Pessoalmente, considero essa equação uma das mais incríveis e belas de toda a matemática. Para mim, ela é a prova de que há algo de divino na matemática.

Dito isso, aqui estão três expansões de Taylor para funções comuns que precisaremos:

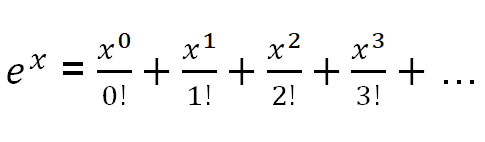
expansões
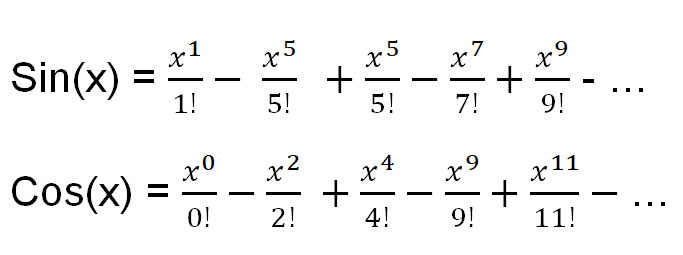
expansions

Vamos usar a expansão de Taylor de e x para encontrar e πi .

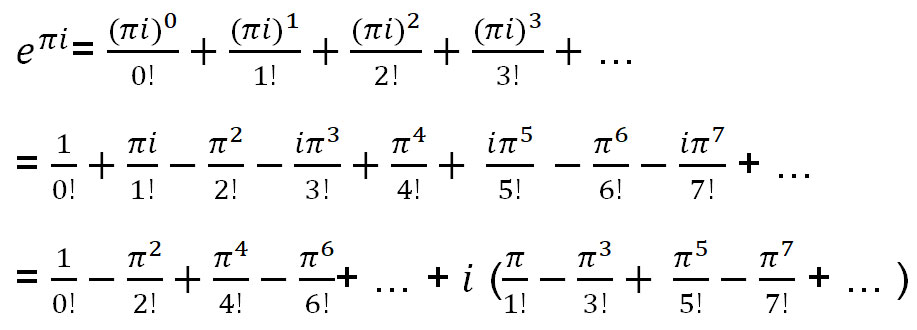
expansões

A equação acima pode ser expressa como funções de sin(x) e cos(x):

= cos(π)+i ×sin⁡(π)

= -1 + i ×0

= -1

Assim, temos e πi = -1. Isso pode ser reorganizado no formato usual:

e πi +1 = 0

Solução de quebra-cabeça lógico

  1. Pegue uma das quatro correntes e abra e separe todos os três elos. Chame as outras três correntes de 1, 2 e 3.
  2. Use um elo para combinar as correntes 1 e 2, criando uma corrente de sete elos.
  3. Use outro elo para combinar a corrente de sete elos da etapa 2 com a corrente 3, criando uma corrente de 11 elos.
  4. Use o último elo para unir as duas extremidades da corrente de 11 elos da etapa 3 para criar um círculo de 12 elos.