Como jogar com as regras de classificação do xadrez

Esta semana, vamos analisar uma fórmula para melhorar seu rating de xadrez sem melhorar seu jogo em nada. Um aviso: trata-se de uma pequena vantagem, de interesse principalmente acadêmico. Mas antes disso, como de costume, apresento nosso quebra-cabeça lógico semanal.

Quebra-cabeça lógico

Há 50 pessoas em fila, numeradas de 1 a 50 sequencialmente. A primeira pessoa da fila é o número 1. Cada pessoa ou sempre diz a verdade ou sempre mente. Todos sabem se os outros estão dizendo a verdade.

Todas as pessoas de número par dizem: "Todos à minha frente são mentirosos".

Todas as pessoas em número ímpar dizem: "Todos atrás de mim são mentirosos."

Quem está dizendo a verdade?

Como jogar com as regras de classificação do xadrez

O sistema de classificação de xadrez mais comum, pelo que sei, é o sistema Elo. Ele recebeu esse nome em homenagem a Arphad Elo. O mesmo sistema também é usado em outros jogos e esportes.

Basicamente, o sistema funciona da seguinte forma: uma fórmula determina a probabilidade de um jogador vencer uma partida, com base nas classificações de ambos os jogadores. O jogador vencedor ganha pontos em proporção à sua probabilidade de perder. Da mesma forma, o jogador perdedor ganha pontos em proporção à sua probabilidade de vencer. Um ponto é atribuído para uma vitória, 0,5 para um empate e 0 para um empate.

O sistema baseia-se na premissa, com a qual concordo, de que o desempenho de um jogador pode ser modelado a partir de um número aleatório extraído da curva normal, sendo a classificação do jogador a média.O jogador que tirar o número mais alto vence.

A probabilidade de ganhar é determinada da seguinte forma:

Seja r1 = classificação do jogador 1.

Seja r2 = classificação do jogador 2.

p = Probabilidade de o jogador 1 vencer.

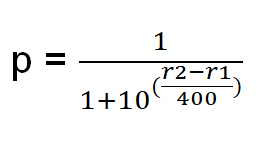
Vejamos um exemplo. Sejam r1=1900 e r2=2000.

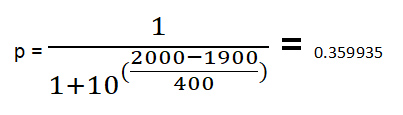
Considerando que 1 ponto seja atribuído para uma vitória e 0 para uma derrota, então o aumento na classificação é de 32*(pontos reais – probabilidade de vitória).

No exemplo acima, se o jogador 1 perder, como previsto, sua classificação cairá 11,52 pontos e a do jogador 2 subirá o mesmo número. Se o jogador 1 vencer, sua classificação subirá 20,48 pontos e a do jogador 2 cairá o mesmo número.

O sistema Elo baseia-se num desvio padrão de desempenho, modelado pelo método de números aleatórios descrito acima, de 200. Presumo que isso seja verdade. No entanto, a fórmula de probabilidade de vitória, na qual as tabelas Elo se baseiam, não é consistente com tal desvio padrão, exceto se a diferença nas classificações for 0 ou 189.

A probabilidade correta de o jogador com a classificação r1 vencer é:

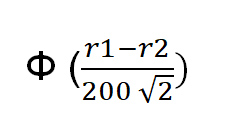
Onde a função Φ(x) = a probabilidade de uma variável aleatória normal padrão ser menor que x. No Excel, a fórmula correta é norm.s.dist((r1-r2)/(200*sqrt(2)),1).

Vamos analisar um caso em que a diferença de rating é de 100. Vamos considerar o jogador 1 como azarão. A fórmula Elo sugere que o jogador 1 tem 35,99% de chance de vencer. No entanto, sua probabilidade real, com base em um desvio padrão de desempenho de 200, é de 36,18%. Em outras palavras, a vitória do jogador 1 é uma boa aposta, enquanto a do jogador 2 é uma má aposta. Mostro que o ganho esperado de rating do jogador 1 e a perda esperada do jogador 2 são de 0,06 pontos.

Em seguida, vamos analisar a diferença de classificação em um cenário de 300 pontos, onde o jogador 1 é o azarão. Aqui, a fórmula Elo dá ao jogador 1 uma probabilidade de 15,10% de vencer, enquanto eu mostro que é de 14,44%. Isso torna a aposta no jogo ruim para o jogador 1 e boa para o jogador 2. A perda esperada para o jogador 1 é de 0,21 pontos, assim como o ganho esperado para o jogador 2.

Os cálculos por trás das probabilidades reais são baseados na curva gaussiana e são mais complexos do que eu gostaria de abordar nesta newsletter.

Em resumo, se a diferença nas avaliações for superior a 189, apostar no favorito é uma boa opção. Da mesma forma, se for inferior a 189, apostar no azarão é uma boa opção.

No entanto, o viés é bastante pequeno. Eu não aceitaria nem recusaria partidas com base nessa informação. Em vez disso, acho que você deveria aceitar qualquer partida por amor ao xadrez.

Leitura complementar: Artigo da Wikipédia sobre o sistema de classificação Elo.

Resposta do quebra-cabeça lógico

As pessoas 2 e 49 são as únicas que estão dizendo a verdade.

Solução de quebra-cabeça lógico

Vamos começar com a pessoa 1. Se ela estiver dizendo a verdade, então todos os outros estão mentindo. No entanto, a pessoa 3 diz que todos, de 4 a 50, estão mentindo.Se isso for verdade, então a pessoa 3 está dizendo a verdade. No entanto, a pessoa 1 diz que ele está mentindo. Isso leva a uma contradição. Portanto, a pessoa 1 deve estar mentindo.

A pessoa 2 afirma apenas que a pessoa 1 está mentindo. Isso faz com que a pessoa 2 esteja dizendo a verdade.

Todas as pessoas de número par, de 4 a 50, dizem que a pessoa 2 está mentindo. Isso faz com que todas elas sejam mentirosas.

A pessoa 49 diz que a pessoa 50 está mentindo, o que é verdade. Isso torna a pessoa 49 sincera.

Todas as pessoas de número ímpar, de 3 a 47, dizem que a pessoa 49 está mentindo. Isso faz com que todas elas sejam mentirosas.

Assim, as únicas pessoas que dizem a verdade são os números 2 e 49.