Demonstração do Teorema do Ângulo Inscrito (parte 1)

Esta semana, retornamos ao meu tema de demonstração de teoremas matemáticos. O teorema desta semana é o Teorema do Ângulo Inscrito. Esta demonstração é mais complexa do que o habitual, por isso, irei dividi-la em duas partes, com a parte 2 na próxima semana. No entanto, antes disso, apresento meu habitual enigma lógico semanal.

Quebra-cabeça lógico

No diagrama abaixo, mova uma moeda para formar duas linhas de quatro moedas cada.

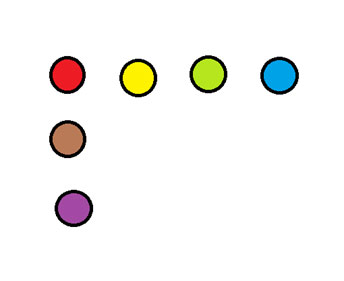
A resposta aparece no final do boletim informativo.

Demonstração do Teorema do Ângulo Inscrito (parte 1)

Antes de explicar o Teorema do Ângulo Inscrito, permita-me definir alguns pontos em um círculo no diagrama a seguir.

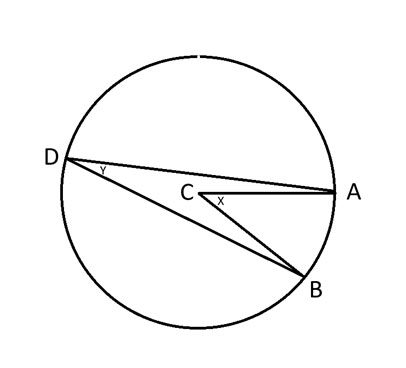
A, B e D = Quaisquer três pontos na circunferência.

C = Centro do círculo.

x = Ângulo ACB.

y = Ângulo ADB.

O teorema do ângulo inscrito afirma que o ângulo 2y = x.

Neste boletim informativo, tentarei provar isso para o caso específico em que AD ou BD formam um diâmetro do círculo. Na próxima semana, expandirei isso para o caso geral da localização de D.

Vamos chamar de Caso 1 o caso específico em que AD forma um diâmetro do círculo. Aqui está um novo diagrama para esse caso.

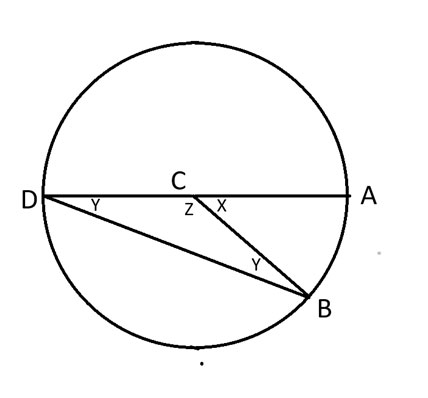
No diagrama acima, AD forma um diâmetro do círculo com C no centro.

Podemos dizer que x + z = 180 graus, porque juntos formam metade dos 360 graus totais de um círculo.

BCD forma um triângulo isósceles. Portanto, o ângulo CDB = CBD = y.

Conforme demonstrado em meu boletim informativo de 13 de novembro de 2025, a soma dos ângulos internos de um triângulo é igual a 180 graus. Em outras palavras, z + 2y = 180 graus.

Vamos reescrever ambas as equações:

z = 180 – x

z = 180 – 2y

Vamos resolver a equação para ambas, já que ambas são iguais a z.

180 – x = 180 – 2y

-x = -2y

x = 2y.

Portanto, demonstramos o caso específico do Teorema do Ângulo Inscrito, onde dois pontos na circunferência formam um diâmetro. Na próxima semana, usaremos esse conhecimento para demonstrar o teorema no caso geral.

Solução de quebra-cabeça lógico

Mova a moeda azul para cima da moeda vermelha. No diagrama abaixo, os números mostram a quantidade de moedas em cada pilha.

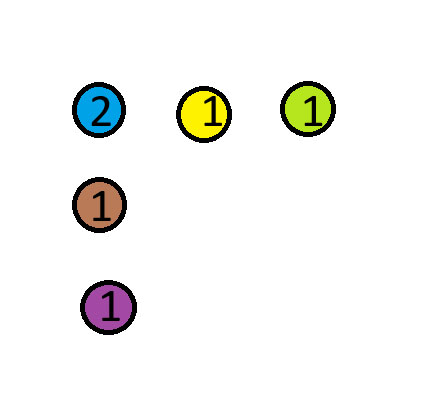
Agradecimento: Peguei este quebra-cabeça do canal Mind Your Decisions no YouTube. Este é o quebra-cabeça nº 3 do vídeo mencionado.