Demonstração do Teorema do Ângulo Inscrito (parte 2)

Vocês devem se lembrar que na semana passada comecei a demonstração do Teorema do Ângulo Inscrito. Esta semana, vamos finalizá-la. No entanto, antes disso, apresento meu habitual quebra-cabeça lógico semanal.

Quebra-cabeça lógico

Quais das seguintes afirmações são verdadeiras?

1. Uma dessas afirmações é falsa.
2. Duas dessas afirmações são falsas.
3. Três dessas afirmações são falsas.
4. Quatro dessas afirmações são falsas.
5. Cinco dessas afirmações são falsas.
6. Seis dessas afirmações são falsas.
7. Sete dessas afirmações são falsas.
8. Oito dessas afirmações são falsas.
9. Nove dessas afirmações são falsas.
10. Dez dessas afirmações são falsas.

A resposta aparece no final do boletim informativo.

Teorema do Ângulo Inscrito (parte 2)

Permita-me relembrar o que diz o Teorema do Ângulo Inscrito.

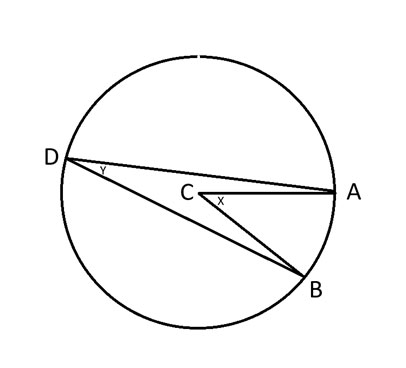
A, B e D = Quaisquer três pontos na circunferência.

C = Centro do círculo.

x = Ângulo ACB.

y = Ângulo ADB.

O teorema do ângulo inscrito afirma que o ângulo 2y = x.

Na semana passada, mostrei que isso é verdade no caso específico em que AD ou BD formavam um diâmetro do círculo. Esta semana, usarei isso para mostrar que o teorema é verdadeiro para o caso geral de D.

Vou detalhar todas as possíveis localizações para D da seguinte forma:

Caso 1 = AD ou BD forma um diâmetro do círculo (provado na semana passada)

Caso 2 = D está localizado (ou seria "está"?) ao longo do arco no lado oposto do círculo em relação a A e B.

Caso 3 = Todos os outros

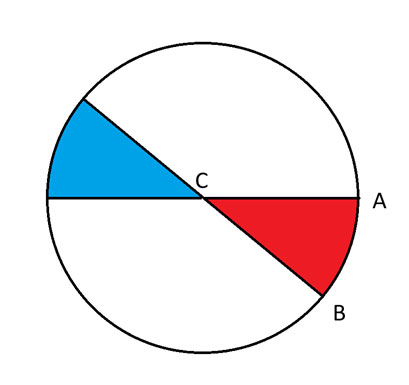
Em outras palavras, o caso 2 abrangerá os casos em que D está na borda do círculo na região azul. O caso 3 abrangerá outras localizações fora dessa faixa azul.

Vamos usar o seguinte diagrama para discussão.

Deixar:

x = x1 + x2

y = y1 + y2

z = z1 + z2

Nosso objetivo é provar que x = 2y

Tracei cuidadosamente uma linha de D a C, formando um diâmetro do círculo. O ponto E é onde essa linha intercepta o outro lado do círculo.

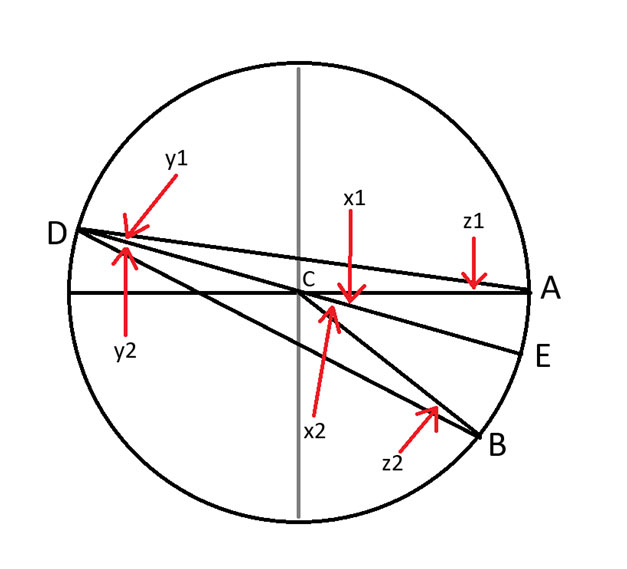
Os números nos ângulos deveriam ter sido subscritos, mas meu software de desenho não permitiu.

Considere o triângulo ADE.

Como DE forma um diâmetro, podemos usar o que provamos na semana passada para mostrar que 2x1 = 2y1.

Agora considere o triângulo EDB.

Pela mesma lógica, _2x² = _y² .

Somando essas equações:

_2x₁ + _2x₂ = _y₁ + _y₂

2( _x₁ + _x₂ ) = _y₁ + _y₂

2x = y

E concluímos o caso 2.

Vamos analisar o caso 3.

Aqui procuramos mostrar que 2x ₁ = y ₁ .

Do caso 1:

_2x² = _y²

2(x ₁ + x ₂ ) = y< ₁ +y ₂

Subtraindo a equação de cima da equação de baixo:

2x ₁ = y ₁

E comprovamos o caso 3.

Resposta do quebra-cabeça lógico

Apenas a afirmação 9 é verdadeira.

Solução de quebra-cabeça lógico

Temos dez declarações contraditórias. Se dez pessoas dizem coisas diferentes, ou apenas uma está certa, ou nenhuma está.

Vamos considerar o caso em que todas as dez afirmações sejam falsas. Isso tornaria a afirmação número 10 verdadeira. Isso faria com que apenas nove afirmações fossem falsas. Portanto, uma contradição. Deve haver uma afirmação verdadeira. Mas qual?

Se uma afirmação é verdadeira, então nove são falsas. É a afirmação número 9 que diz isso. Portanto, apenas a afirmação 9 é verdadeira.