Quebra-cabeça matemático gigante para chamada de Zoom
A seguinte pergunta foi feita na minha newsletter da semana passada. Caso precise relembrar, aqui está a pergunta.
Pergunta
Suponha que todos os 435 membros votantes da Câmara dos Representantes dos EUA participem da mesma chamada do Zoom, agendada para ocorrer das 9h às 10h. No entanto, não é obrigatório participar de toda a chamada, apenas de alguma parte dela. Cada membro escolhe aleatoriamente um momento exato para entrar e sair da chamada dentro desse intervalo de uma hora.
Qual a probabilidade de pelo menos um representante aparecer ao mesmo tempo que todos os outros representantes na chamada? Em outras palavras, ver o rosto de todos os outros membros durante o tempo em que estiverem na chamada, não necessariamente todos ao mesmo tempo.
Por favor, role a tela para baixo, passando pelas imagens, para ver minha resposta e solução.

Responder
2/3
Solução
Minha estratégia geral com questões que envolvem um grande grupo de pessoas é começar com duas. Depois de encontrar a resposta, passo para três. Então, se não for muito difícil, passo para quatro. Se eu perceber um padrão, há boas chances de que esse padrão se aplique a qualquer número de pessoas.
Revisão de Matemática Básica
Antes de prosseguir, vou usar frequentemente a função combin(x,y). Ela representa o número de maneiras de escolher y itens de um grupo de x. Por exemplo, o número de maneiras de escolher cinco cartas de um conjunto de 52, onde a ordem não importa, é combin(52,5) = 2.598.960. A resposta pode ser expressa como x! / (y! * (xy)!).
Neste caso, o ponto de exclamação não significa que estou gritando, mas representa a função fatorial. Esta é o número de maneiras de ordenar qualquer quantidade de itens. Por exemplo, se você precisa ler seis livros, um de cada vez, o número de ordens possíveis dos livros é 6!. A resposta para o caso geral de n é 1*2*3*…*n. No caso dos seis livros, a resposta é 1*2*3*4*5*6 = 720.
Caso de duas pessoas
Dito isso, vamos resolver o problema para o caso de duas pessoas. Os horários exatos em que as pessoas entram e saem da chamada não importam, apenas a ordem dos eventos. Vamos usar uma letra para representar a entrada/saída de uma pessoa específica na chamada. Da esquerda para a direita, a primeira vez que uma determinada letra for usada representará a entrada na chamada e a segunda, a saída.
6;font-family: 'Open Sans',sans-serif;color: #313131!important">Dos quatro locais no histórico de chamadas, existem combin(4,2)=6 maneiras de colocar a letra A:1. AABB
2. ABAB
3. ABBA
4. BAAB
5. BABA
6. BBAA
Vamos verificar se ambos os interlocutores estavam online ao mesmo tempo em cada cenário:
1. AABB - Não, A chegou e saiu antes de B entrar na chamada.
2. ABAB - Sim, houve sobreposição entre a chegada de B e a saída de A.
3. ABBA - Sim, houve sobreposição entre a chegada de B e a saída de B.
4. BAAB - Sim, houve sobreposição entre a chegada de A e a partida de A.
5. BABA - Sim, houve sobreposição entre a chegada de A e a partida de B.
6. BBAA - Não, B chegou e saiu antes de A entrar na chamada.
Cada cenário tem a mesma probabilidade. Quatro dos seis cenários apresentaram sobreposição, portanto a probabilidade de sobreposição no caso de duas pessoas é de 2/3.
Caso de três pessoas
O número de históricos de chamadas no caso de três pessoas é o produto do número de maneiras que a pessoa A pode escolher dois lugares dentre os 6 no histórico e o número de maneiras que a pessoa B pode escolher 2 dentre os 4 lugares restantes. Isso é igual a combin(6,2)*combin(4,2) = 15*6 = 90.
Seria tedioso listar todos os 90. Vamos simplificar as coisas assumindo que a pessoa A entra primeiro. Alguém tem que ser o primeiro, então pode muito bem ser A.
Primeiro, vamos considerar a situação em que o próximo evento no histórico da chamada é a saída de A. Vamos representar isso como AA????. Não importa como B e C entrem e saiam da chamada, ninguém irá sobrepor A. Assim, o cenário AA tem uma probabilidade de sucesso de 0. A probabilidade do próprio cenário AA é 1/5, porque depois que A ocupou o primeiro lugar, havia cinco eventos possíveis para acontecer em seguida – A, B, B, C e C.
Em segundo lugar, vamos considerar a situação em que A entra primeiro, B entra em seguida e, por fim, A sai. Nesse caso, B representa qualquer pessoa diferente de A (que já encerrou a chamada). Isso é representado como ABA???. As letras restantes a serem posicionadas são B, C e C. Das três maneiras de posicionar B (BCC, CBC e CCB), CBC e CCB resultam na sobreposição de B tanto com A quanto com C.Assim, a probabilidade de sucesso no cenário ABA é 2/3. A probabilidade desse cenário em si é pr(qualquer pessoa diferente de A entra)*pr(A sai) = (4/5)*(1/4) = 1/5, onde pr(x) representa a probabilidade do evento x.
Em terceiro lugar, vamos considerar a situação em que A entra primeiro, B entra em seguida e, por fim, B sai. Isso é representado como ABB???. As letras restantes a serem colocadas são A, C e C. Das três maneiras pelas quais A pode ser colocado (ACC, CAC e CCA), CAC e CCA resultam em A sobrepondo-se a B e C. Assim, a probabilidade de sucesso no cenário ABB é 2/3. A probabilidade desse cenário em si é pr(qualquer pessoa diferente de A entra)*pr(B sai) = (4/5)*(1/4) = 1/5.
Em quarto lugar, vamos considerar a situação em que A entra primeiro, B entra em seguida e, por fim, C entra. Isso é representado como ABC??? As letras restantes a serem colocadas são A, B e C. É fácil ver que, onde quer que A saia da chamada, ele se sobreporá a B e C. Portanto, a probabilidade de sucesso nesse cenário é 1. A probabilidade desse cenário em si é pr(qualquer pessoa que não seja A entrar) * pr(uma terceira pessoa entrar) = (4/5) * (2/4) = 2/5.
Analisamos todos os cenários possíveis, como evidenciado pelas probabilidades (1/5 + 1/5 + 1/5 + 2/5) que somam 1. Calculando o produto escalar da probabilidade de cada cenário e sua probabilidade de sucesso, obtemos: (1/5)*0 + (1/5)*(2/3) + (1/5)*(2/3) + (2/5)*1 = 0 + 2/15 + 2/15 + 6/15 = 10/15 = 2/3.
Caso de quatro pessoas
Se eu estivesse com pouco tempo, talvez chutasse que a resposta para a pergunta original fosse 2/3, já que isso vale para os casos com 2 e 3 pessoas. No entanto, isso parece tão insatisfatório, então vamos analisar o caso com quatro pessoas.Posso dividir isso em dez cenários possíveis, como segue:
- AA??????
Probabilidade do cenário = 1/7
Probabilidade de sucesso = 0 (ninguém pode sobrepor-se a A)
- ABA????
Probabilidade do cenário = 1/7
Probabilidade de sucesso = 16/30
- ABBA????
Probabilidade do cenário = 1/35
Probabilidade de sucesso = 0 (ninguém pode sobrepor-se a B)
- ABCB????
Probabilidade do cenário = 4/35
Probabilidade de sucesso = 2/3
- ABCA????
Probabilidade do cenário = 4/35
Probabilidade de sucesso = 5/6
- ABCBA????
Probabilidade do cenário = 1/35
Probabilidade de sucesso = 2/3
- ABCBC????
Probabilidade do cenário = 1/35
Probabilidade de sucesso = 2/3
- ABCBD????
Probabilidade do cenário = 2/35
Probabilidade de sucesso = 1 (A irá sobrepor-se a B, C e D)
- ABCC????
Probabilidade do cenário = 4/35
Probabilidade de sucesso = 5/6
- ABCD????
Probabilidade do cenário = 8/35
Probabilidade de sucesso = 1 (A irá sobrepor-se a B, C e D)
Peço desculpas por não ter detalhado os cálculos matemáticos de cada situação com a mesma precisão, mas não queria que esta solução ficasse muito extensa e preferi deixar algum trabalho para o leitor.
A tabela a seguir resume todos os dez cenários do caso com quatro pessoas.
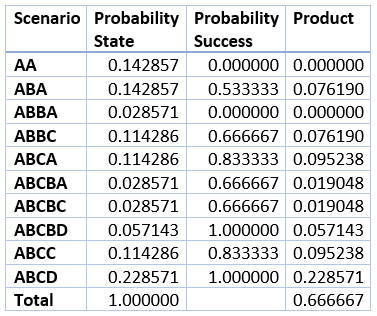
A célula inferior direita da tabela mostra uma probabilidade de 2/3.
Resumo
Mostramos uma probabilidade de 2/3 para os casos de duas, três e quatro pessoas. É razoável supor que essa probabilidade provavelmente continuará válida para qualquer número de pessoas. Simulações e cálculos matemáticos realizados por pessoas mais inteligentes do que eu comprovaram essa hipótese.

