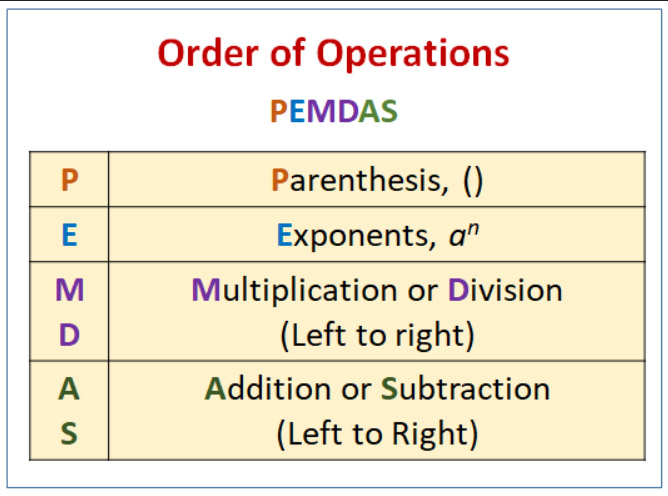
Como aplicar a regra PEMDAS.

Se você é como eu, recebe uma enxurrada de perguntas sobre a ordem das operações no seu feed do Facebook. Todas elas são seguidas por centenas de respostas nos comentários, nas quais a maioria das pessoas está errada. O número de pessoas que admitem que estavam erradas é invariavelmente zero.

O que torna minha opinião correta? Primeiro, se me permitem um pouco de autoelogio, gostaria de pensar que sou reconhecido como uma das principais fontes de informação sobre a matemática dos jogos de cassino. Pesquise qualquer jogo ou termo relacionado a cassino e você encontrará meu nome em todos os lugares. Além disso, sou formado em matemática e economia pela Universidade da Califórnia em Santa Bárbara e sou um associado aposentado da Sociedade de Atuários. Tudo o que tenho feito desde que me formei na faculdade tem sido de natureza matemática.

Um exemplo de tal pergunta é:

6 ÷ 2 (1 + 2) = ?

Pare por um momento e pense nisso.

Se você respondeu 1, está errado. Acredito que você esteja errado porque está seguindo a regra prática PEMDAS para a ordem das operações. Essa é uma técnica mnemônica ensinada por volta do 5º ano do Ensino Fundamental. Uma forma de memorizá-la que me ensinaram é "Por favor, desculpe minha querida tia Sally". Ela serve para ensinar as crianças a avaliar uma expressão na seguinte ordem:

1. 1. Parênteses
2. 2. Expoentes
3. 3. Multiplicação
4. 4. Divisão
5. 5. Aritmética
6. 6. Subtração

Seu professor do ensino fundamental provavelmente acreditava que isso estava correto. No entanto, não está. Não sei onde isso começou, mas suspeito que seja um recurso mnemônico simplificado que crianças de 10 anos entendem facilmente. O problema de simplificar qualquer coisa é que, embora possa levar à resposta correta na maioria das vezes, geralmente há exceções à regra.No caso da ordem PEMDAS, isso levaria alguém a resolver o problema 6 ÷ 2 (1 + 2) mencionado anteriormente desta forma:

1. 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) porque você avalia os parênteses primeiro
2. 6 ÷ 2 (3) = 6 ÷ 2 × 3 porque nenhum operador fora dos parênteses implica multiplicação
3. 6 ÷ 2 × 3 = 6 ÷ 6 porque a multiplicação é feita antes da divisão, de acordo com a ordem das operações (PEMDAS).
4. 6 ÷ 6 = 1

O erro na lógica acima está no terceiro passo. A multiplicação nem sempre vem antes da divisão. Elas têm a mesma precedência. Quando ambas aparecem na mesma expressão, faça primeiro a que está mais à esquerda.

Gostaria de acrescentar que a adição não precisa necessariamente vir antes da subtração. Ambas têm a mesma precedência. No entanto, nesse caso de adição e subtração, em que regras superiores não se aplicam, não importa qual você faça primeiro.

Eis a maneira correta de calcular 6 ÷ 2 (1 + 2):

1. 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) porque você avalia os parênteses primeiro
2. 6 ÷ 2 (3) = 6 ÷ 2 × 3 porque nenhum operador fora dos parênteses implica multiplicação
3. 6 ÷ 2 × 3 = 3 × 3 porque, tanto na multiplicação quanto na divisão, você avalia primeiro da esquerda para a direita.
4. 3 × 3 = 9

Aqui vai outra pergunta para você:

7 + 7 ÷ 7 + 7 × 7 – 7 = ?

No Facebook, você vê a resposta dada como 56. Essa é uma resposta errada que as pessoas dão não por causa da ordem das operações (PEMDAS), mas porque "Minha calculadora disse que a resposta é 56". Essa é uma resposta preguiçosa e incorreta dada por quem simplesmente lê da esquerda para a direita.O raciocínio incorreto é:

1. 7 + 7 ÷ 7 + 7 × 7 – 7 = 14 ÷ 7 + 7 × 7 – 7 porque você avalia primeiro da esquerda para a direita
2. 14 ÷ 7 + 7 × 7 – 7 = 2 + 7 × 7 – 7 porque você avalia primeiro da esquerda para a direita
3. 2 + 7 × 7 – 7 = 9 × 7 – 7 porque você avalia primeiro da esquerda para a direita
4. 9 × 7 – 7 = 63 – 7 porque você avalia primeiro da esquerda para a direita
5. 63 – 7 = 56

A forma correta de avaliar isso é:

1. 7 + 7 ÷ 7 + 7 × 7 – 7 = 7 + 1 + 7 × 7 – 7 porque a divisão precede a adição e está à esquerda da multiplicação.
2. 7 + 1 + 7 × 7 – 7 = 7 + 1 + 49 – 7 porque a multiplicação é mais importante que a adição e a subtração.
3. 7 + 1 + 49 – 7 = 8 + 49 – 7 porque entre a adição e a subtração, faça primeiro a operação mais à esquerda.
4. 8 + 49 – 7 = 57 – 7 porque entre a adição e a subtração, faça primeiro a operação mais à esquerda.
5. 57 – 7 = 50

Observe que esta é uma regra que a PEMDAS aplica corretamente. As pessoas erram por não usarem suas calculadoras da maneira certa. É crucial inserir os números e as operações na ordem correta. Isso é muito mais fácil de fazer com calculadoras que usam a notação polonesa reversa, como a HP15C. Aliás, qualquer pessoa que tenha uma HP15C ou 12C já é minha amiga.

Para finalizar, gostaria de dar meu toque pessoal a esses quebra-cabeças de ordem das operações com este que eu mesmo criei, tanto na lógica quanto no layout. Admito que peguei as imagens do Google. Este quebra-cabeça foi inspirado em um similar, porém ainda mais difícil, do canal Mind Your Decisions no YouTube. Compartilhe onde quiser; espero que viralize.

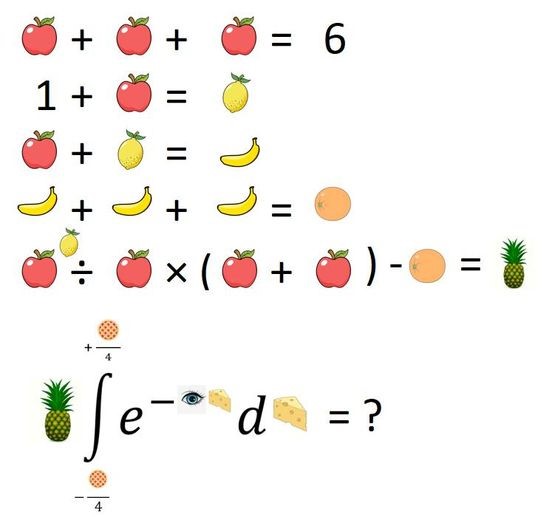
Crédito parcial para quem resolver apenas o valor do abacaxi e crédito total para quem resolver a integral.

Publicarei as respostas no boletim informativo de 29 de junho. Até lá, que a sorte esteja sempre ao seu lado.

Escrito por: Michael Shackleford