Como ganhar o jogo "O Preço Certo": "Agora ou Depois"

Um dos meus interesses fora do mundo dos jogos de azar são os programas de jogos. Em particular, adoro o aspecto da teoria dos jogos presente em muitos deles. Especialmente "The Price is Right". Adoraria escrever um livro sobre a maneira matematicamente ideal de jogar todos os jogos desse programa sem nenhum conhecimento prévio dos preços.

Nesta newsletter, abordarei apenas um jogo: "Now or Then".

Eis as regras:

1. Há um tabuleiro circular com seis fatias, como uma roda do jogo Trivia Pursuit. Para fins de discussão, vamos numerar as fatias assim.
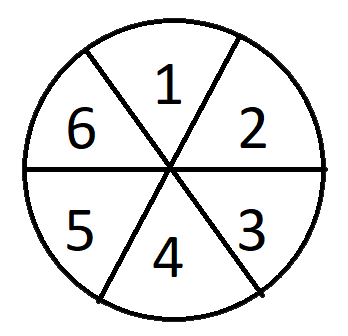
2. Cada preço será o preço exato "Atual" ou o preço praticado há cerca de dez anos.
3. O jogador pode escolher qualquer fatia.
4. O jogador deve adivinhar se o item na fatia selecionada exibe o preço específico para "Agora" ou "Antes".
5. O jogador deve acertar três fatias consecutivas na roleta (por exemplo, as fatias 4, 5 e 6) para ganhar o jogo.
6. Embora não seja mencionado no programa, tradicionalmente são apresentados quatro itens "Atual" e dois "Antigamente".

Levando em consideração as informações acima, existe uma maneira de garantir a vitória neste jogo sem saber o preço de nada. As regras 2 e 6 são cruciais. Creio que poucos participantes conhecem ambas as regras.

Aqui está um exemplo no YouTube.

Observe, aos 3:52, como Drew afirma corretamente que o jogador precisa acertar os pretzels para ganhar; mas ele acrescenta: "No entanto, você pode ir para onde quiser."

Link para o site de fãs: https://priceisright.fandom.com/wiki/Now....or_Then

A resposta é revelada abaixo das imagens retiradas do programa.

Aqui está a resposta:

Primeiro, escolha três fatias quaisquer em sequência e tente adivinhar "Agora" para todas elas. Por exemplo, as três de cima, que são 6, 1 e 2.

6;font-family: 'Open Sans',sans-serif;color: #313131!important">Aqui está como proceder, de acordo com o que aconteceu com as três primeiras fatias.

1. Se os três fossem AGORA, então você ganharia!
2. Se duas delas forem "ENTÃO", então as restantes devem ser "AGORA". Garanta a vitória escolhendo "AGORA" para as outras três fatias.
3. Se você encontrar um "ENTÃO" em qualquer uma das extremidades (fatia 2 ou 6), tente adivinhar qualquer coisa para as duas fatias mais próximas da fatia com o "ENTÃO". Se você encontrar o outro "ENTÃO", a fatia restante deve ser "AGORA". Se você não encontrar o outro "ENTÃO", então o último "ENTÃO" deve ser a última fatia. Observe que essa era a situação no vídeo de exemplo que mencionei acima, mas o jogador não seguiu a dica de Drew de tentar obter informações em fatias diferentes daquela necessária.
4. Se você acertar "ENTÃO" no meio (fatia 1), escolha "AGORA" para as fatias 3 e 5. Se ambas forem "AGORA", você ganha escolhendo "ENTÃO" para a fatia 4. Se uma for "ENTÃO", escolha "AGORA" para a fatia 4 e ganhe.

Em outras palavras, trata-se de saber que existem duas fatias THEN e de restringir a localização delas.

Para o boletim informativo da próxima semana, vou dar a pergunta agora para que vocês tenham uma semana inteira para se divertirem trabalhando nela!

Suponha que todos os 435 membros votantes da Câmara dos Representantes dos EUA participem da mesma chamada do Zoom, agendada para das 9h às 10h. No entanto, não é obrigatório participar da chamada inteira, apenas de alguma parte dela. Cada membro escolhe aleatoriamente um momento exato para entrar e sair da chamada dentro desse intervalo de uma hora.

Qual a probabilidade de pelo menos um representante aparecer ao mesmo tempo que todos os outros representantes na chamada? Em outras palavras, ver o rosto de todos os outros membros durante o tempo em que estiverem na chamada, mas não necessariamente todos ao mesmo tempo.

Escrito por: Michael Shackleford