Concorrentes do programa "The Price is Right" se enfrentam

Antes de abordar o assunto principal, uma atualização. Na semana passada, escrevi sobre o processo para conseguir ingressos para o Burning Man. Na quarta-feira, arrisquei na venda principal. Como vocês devem se lembrar, o último requisito era estar pronto para comprar os ingressos exatamente ao meio-dia do dia 30 de março. Eu estava pronto. Na verdade, eu tinha três navegadores abertos com o link da venda. Para ser sincero, não sei se isso aumentou minhas chances, mas outras fontes sobre o Burning Man recomendam fazer isso.

Resumindo, não consegui ingresso. Era de se esperar. Pelo menos tentei. Diferentemente de 2019, a imagem que você vê abaixo nas minhas telas foi atualizada cerca de meia hora após o início das vendas, informando que os ingressos estavam esgotados. Você pode estar se perguntando se eu cliquei em "voltar", o que, segundo a tela, não adiantaria. Não cliquei.

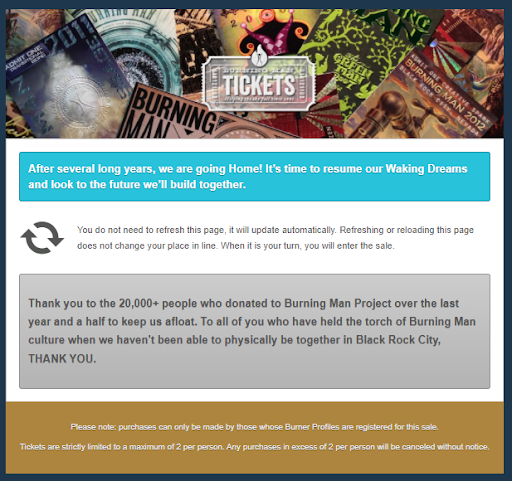
Então, parece que não vou conseguir ir ao Burning Man este ano. Tudo bem. Tenho várias outras ideias para as férias.

Vamos ao assunto principal: a Fileira dos Participantes no programa The Price is Right. Essa brincadeira acontece seis vezes em cada episódio. Para quem ainda não conhece, aqui estão as regras:

1. Quatro jogadores são escolhidos para competir no próximo jogo de precificação.
2. É apresentado um item que geralmente terá um valor entre US$ 1.000 e US$ 2.000. Por exemplo, uma bela bicicleta.
3. Os jogadores, em uma ordem específica, farão um lance sobre o valor do item.
4. O jogador cujo lance se aproximar mais do valor real, sem ultrapassá-lo, ganha o item e poderá jogar a próxima rodada de precificação.
5. Se todos os quatro jogadores derem lances acima do valor mínimo, eles repetem seus lances, na mesma ordem, sendo instruídos a não oferecerem um valor superior ao lance mais baixo da rodada anterior. Isso continuará até que haja uma rodada em que pelo menos um jogador não dê um lance acima do valor mínimo.

Qual deve ser sua estratégia neste jogo, supondo que você não saiba nada sobre o valor do prêmio?

A maioria dos participantes do programa tem uma estratégia péssima. Digamos que você seja o último a dar um lance e os lances anteriores sejam de US$ 1.500, US$ 1.600 e US$ 2.400. Os melhores lances, sem saber nada sobre o valor do item, seriam:

• US$ 1: Isso cobre uma faixa de US$ 1499 - valores de US$ 1 a US$ 1499, embora os prêmios nunca cheguem perto de US$ 1.
• US$ 1.601: Este valor abrange uma faixa de US$ 800 – valores entre US$ 1.600 e US$ 2.399.
• $2401: Este valor abrange uma gama infinita – de $2.400 ao infinito.

É comum vermos jogadores fazendo lances que abrem mão de uma faixa de preço desnecessariamente. No exemplo acima, US$ 2.000. Isso significa abrir mão da faixa de US$ 1.600 a US$ 1.999, em comparação com um lance de US$ 1.600, sem nenhum benefício.

Não existe uma regra geral que funcione para todas as situações. Tente apenas abranger o máximo possível, especialmente na faixa em que os prêmios costumam ser distribuídos.

E se quatro lógicos estivessem jogando, você pode perguntar? Vamos supor que os lógicos não saibam nada sobre o valor do prêmio. Para facilitar as explicações, vamos supor que os competidores possam dar lances até o centavo.

Vamos começar com uma situação simples em que o valor do prêmio é aleatório e escolhido a partir de uma distribuição uniforme de $0 a $1000. Obviamente, há uma vantagem posicional em ser o último a dar o lance. Não vou entrar em detalhes matemáticos, mas aqui está como os quatro lógicos devem dar seus lances, na ordem em que derem o primeiro ao último:

• Jogador 1: $777,80
• Jogador 2: $555,57
• Jogador 3: $333,33
• Jogador 4: $0,01, $333,34, $555,57 ou $777,79.

A estratégia principal é que os três primeiros jogadores querem levar todos os jogadores subsequentes a um ponto próximo da indiferença. Cada um deles busca reduzir o máximo de espaço possível, sem motivar um jogador subsequente a oferecer US$ 0,01 a mais do que eles.

Se eles fizerem os lances dessa forma, o jogador 4 terá 33,3% de chance de ganhar, independentemente dos quatro lances possíveis que listei para ele. Cada um dos outros jogadores terá 22,2% de chance de ganhar. Adicionei um ou dois centavos aos lances dos jogadores 1 e 2 para garantir que os jogadores 3 e 4 não os superassem em US$ 0,01.

No entanto, este é um exemplo irrealista, já que o valor dos prêmios tende a seguir uma distribuição exponencial. Para torná-lo mais realista, suponha que o valor do prêmio seja escolhido aleatoriamente a partir de uma distribuição exponencial com média de US$ 1.000.

Sem entrar em detalhes matemáticos, aqui estão os lances ótimos considerando a hipótese acima:

• Jogador 1: $ 1.504,08
• Jogador 2: $810,98
• Jogador 3: $405,47
• Jogador 4: $0,01, $405,48, $810,99 ou $1.504,09

As probabilidades de vitória serão as mesmas do primeiro caso, 33,3% para o jogador 4 e 22,22% para todos os outros.

Por esta semana é tudo. Até a próxima, que a sorte esteja ao seu lado.

Escrito por: Michael Shackleford