Loucura de Março de 2025
Quebra-cabeça lógico
Antes de abordarmos o tema desta semana, as estatísticas do March Madness, é hora do nosso tradicional quebra-cabeça lógico semanal. Aqui está ele.
Três jogadores participam de um jogo. Sem que os jogadores vejam, três moedas são lançadas, uma para cada jogador. De acordo com o resultado de cada lançamento, o jogador é vendado e recebe um chapéu preto ou branco. As vendas são então removidas e cada jogador pode ver os chapéus dos outros dois jogadores, mas não o seu próprio.
Em seguida, cada jogador recebe uma cédula secreta para registrar a cor do seu chapéu. As opções são preto, branco e "passar". Para que o experimento seja um sucesso, todos os jogadores que votarem em branco ou preto devem estar corretos. No entanto, se os três jogadores votarem em "passar", o experimento fracassa.
Os jogadores têm algum tempo para elaborar uma estratégia. Que estratégia eles podem usar que resultará em 75% de chance de sucesso?
Atualização sobre o March Madness
Eu costumava apostar pesado em apostas de proposição do March Madness. Um exemplo típico seria um "mais/menos" sobre quantas partidas seriam vencidas pelas equipes da conferência Pacific 12. Para analisar essas apostas, era útil saber quantas partidas cada equipe, determinada posição no ranking, poderia esperar vencer.
Algumas apostas são resolvidas na primeira rodada. Em particular, será que um time com a 13ª ou maisª posição vencerá uma partida? Aqui estão alguns exemplos de apostas feitas por Covers este ano.
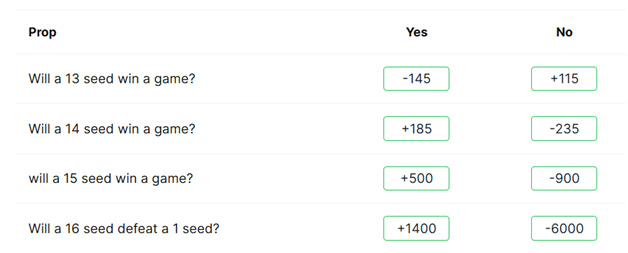
A tabela a seguir mostra a probabilidade de uma equipe específica, com uma determinada classificação, vencer uma partida na primeira rodada, bem como a probabilidade de qualquer uma das quatro equipes com essa classificação vencer. Ela se baseia nos 40 anos do torneio da NCAA, de 1985 a 2025.
| Semente | Vitórias de equipes específicas | Qualquer equipe vence a primeira rodada. |
|---|---|---|
| 1 | 98,75% | 100,00% |
| 2 | 92,50% | 100,00% |
| 3 | 85,63% | 99,96% |
| 4 | 79,38% | 99,82% |
| 5 | 64,38% | 98,39% |
| 6 | 61,25% | 97,75% |
| 7 | 61,25% | 97,75% |
| 8 | 50,00% | 93,75% |
| 9 | 50,00% | 93,75% |
| 10 | 38,75% | 85,93% |
| 11 | 38,75% | 85,93% |
| 12 | 35,63% | 82,83% |
| 13 | 20,63% | 60,31% |
| 14 | 14,38% | 46,25% |
| 15 | 7,50% | 26,79% |
| 16 | 1,25% | 4,91% |
Este ano, a média de classificação para passar da primeira rodada foi de 5,34. A média geral do torneio é de 5,84.
Na segunda rodada, a média de classificação para avançar até as oitavas de final foi de 3,44. A média do torneio é de 4,52. O jogador com a pior classificação a avançar para a segunda rodada foi o 10º colocado. Em outras palavras, os azarões não se saíram bem nas duas primeiras rodadas deste ano.
Na terceira rodada, a média de classificação para chegar às quartas de final foi de 1,625. A média do torneio é de 3,30. O jogador com a classificação mais baixa a sobreviver a três jogos foi o de número 3, sendo que houve apenas um caso. Isso iguala o recorde do torneio para o jogador com a classificação mais baixa a sobreviver, também de número 3. Tal fato já havia ocorrido duas vezes antes, em 2007 e 2009. A média de classificação de 1,625 estabelece um novo recorde negativo na história do torneio.
Na semifinal, todas as quatro equipes eram cabeças de chave número 1. Isso só aconteceu uma vez antes na história do torneio, em 2008. Existe uma aposta popular sobre o número exato de equipes cabeças de chave número 1 que chegarão à semifinal. Aqui está a aposta de Covers deste ano.
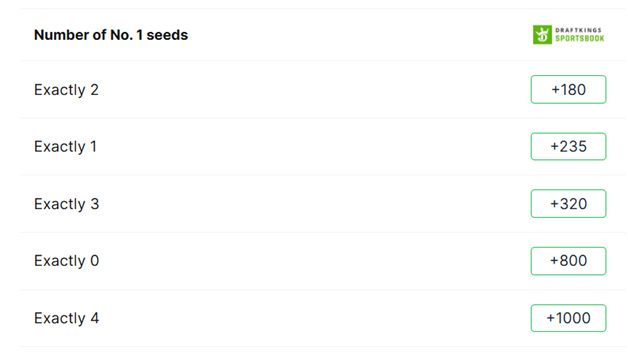
A tabela a seguir mostra quantos times cabeças de chave número um chegaram à Final Four nos 40 anos de história do torneio.
| #1 Sementes | Contar | Probabilidade |
|---|---|---|
| 4 | 2 | 5,00% |
| 3 | 4 | 10,00% |
| 2 | 15 | 37,50% |
| 1 | 16 | 40,00% |
| 0 | 3 | 7,50% |
| Total | 40 | 100,00% |
A probabilidade de um time específico, cabeça de chave número um, chegar às semifinais é de 41,25%.
É evidente que, com todas as quatro equipes nas semifinais sendo cabeças de chave número um, duas delas chegariam à final e provavelmente a venceriam.
Outra aposta especial é a do cabeça de chave que vencerá o jogo do campeonato. Aqui estão as apostas Covers deste ano.
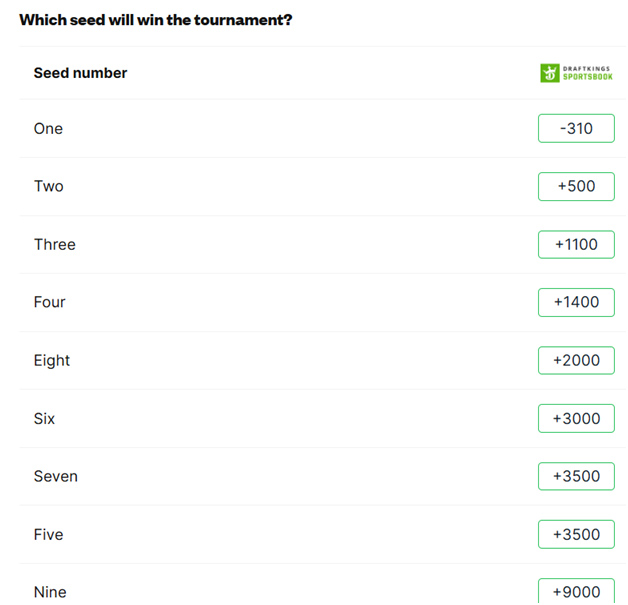
A tabela a seguir mostra a frequência com que cada cabeça de chave venceu o Jogo do Campeonato.
| Cabeça de chave vencedora | Contar | Probabilidade |
|---|---|---|
| 1 | 26 | 65,00% |
| 2 | 5 | 12,50% |
| 3 | 4 | 10,00% |
| 4 | 2 | 5,00% |
| 5 | 0 | 0,00% |
| 6 | 1 | 2,50% |
| 7 | 1 | 2,50% |
| 8 | 1 | 2,50% |
| 9 a 16 | 0 | 0,00% |
| Total | 40 | 100,00% |
Voltando às vitórias esperadas por posição de classificação, aqui está uma tabela atualizada, incluindo dados desta temporada.
| Semente | Vitórias médias |
|---|---|
| 1 | 3,34 |
| 2 | 2,33 |
| 3 | 1,84 |
| 4 | 1,56 |
| 5 | 1.14 |
| 6 | 1.06 |
| 7 | 0,89 |
| 8 | 0,73 |
| 9 | 0,59 |
| 10 | 0,61 |
| 11 | 0,64 |
| 12 | 0,51 |
| 13 | 0,24 |
| 14 | 0,16 |
| 15 | 0,11 |
| 16 | 0,01 |
Uma pergunta que me fazem com frequência é a probabilidade de um palpite perfeito. Considerando uma estratégia de sempre escolher o jogo com a melhor classificação (ou o de menor número) em todas as situações, exceto em confrontos diretos, minha probabilidade atualizada, incluindo dados desta temporada, é de 1 em 287.548.153.
Resposta do quebra-cabeça lógico
A estratégia deve ser a seguinte:
- • Se você vir dois chapéus de cores opostas, passe.
- • Se você vir dois chapéus da mesma cor, escolha a cor oposta.
Eis o que podemos esperar que aconteça de acordo com as três cores:
- • Três pretas: Todos os jogadores verão duas pretas e votarão na branca. Todos errarão, então o experimento falhará.
- • Dois pretos, um branco: O jogador branco verá dois chapéus pretos e votará corretamente no branco. Os dois jogadores pretos verão um de cada cor e passarão a vez. O experimento foi um sucesso.
- • Um preto, dois brancos: O jogador com o chapéu preto verá dois chapéus brancos e votará corretamente no preto. Os dois jogadores com o chapéu branco verão um de cada cor e passarão a vez. O experimento foi um sucesso.
- • Três brancas: Todos os jogadores verão duas brancas e votarão em pretas. Todos errarão, então o experimento falhará.
A probabilidade de haver três brancos ou três negros é 2*(1/2) ³ = 25%. A alternativa é uma divisão de 2 para 1 entre as duas cores, com 75% de probabilidade. Como mostrado acima, com uma divisão de 2 para 1, o experimento será bem-sucedido.


