Problema de matemática de Meninas Malvadas

Você deve se lembrar que na newsletter da semana passada eu apresentei o segundo problema de matemática do filme Gênio Indomável. Você deve se lembrar que o filme afirmava que o departamento de matemática do MIT levou dois anos para resolvê-lo. Como mostrei na semana passada, o problema não só era bastante fácil, como o personagem gênio da matemática interpretado por Matt Damon só conseguiu fornecer 80% da resposta.

Esta semana vamos analisar outro filme que tem um problema de matemática como um ponto importante da trama. O filme é Meninas Malvadas. Em uma competição de matemática do ensino médio, tudo se resume à personagem Cady, interpretada por Lindsay Lohan, respondendo à seguinte pergunta:

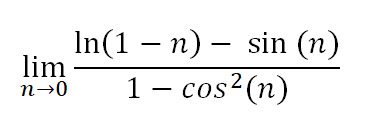
Você pode ver a cena em questão no seguinte vídeo do YouTube. A pergunta é feita a partir dos 4 minutos e 53 segundos.

Se pudéssemos usar uma planilha, veríamos facilmente que, à medida que x se aproxima de 0 pelo lado negativo, f(x) tende ao infinito. À medida que x se aproxima de 0 pelo lado positivo, f(x) tende ao infinito negativo. Portanto, podemos ver com a ajuda de um computador que, como a função tende tanto ao infinito negativo quanto ao positivo, ela não tende a nenhum valor específico. Logo, o limite não existe.

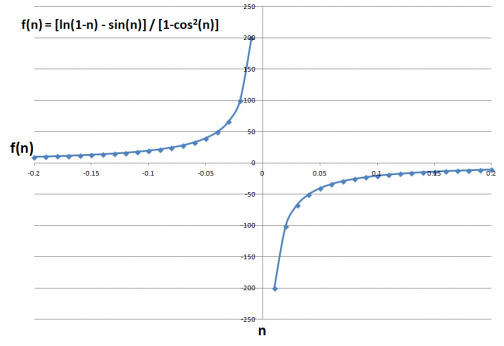
No entanto, eles não tinham permissão para usar computadores no filme. Para ajudar a resolver o problema, permita-me lembrar a Regra de L'Hôpital.

Basicamente, isso significa que se o limite de f(x)/g(x) = 0/0, então lim f(x)/g(x) = lim f'(x)/g'(x). Consulte o link acima para outras condições que não listarei aqui.

Por favor, não me escrevam dizendo que esqueci de colocar um acento circunflexo sobre o "o" em "L'Hospital". Acho que ambas as grafias são aceitáveis. Ainda não tenho certeza de como pronunciar e fico feliz por não ter que fazê-lo para este boletim informativo.

Primeiramente, gostaria de apresentar outro problema onde a aplicação da Regra de L'Hôpital é apropriada. Este exemplo foi retirado da página da Wikipédia que mencionei anteriormente.

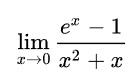
Tanto o numerador quanto o denominador tendem a 0 quando o limite de x se aproxima de 0. Não podemos fazer nada com 0/0. Pela regra de L'Hôpital, podemos calcular a derivada do numerador e do denominador e tomar o limite dessa fração quando x tende a zero. Vamos fazer isso.

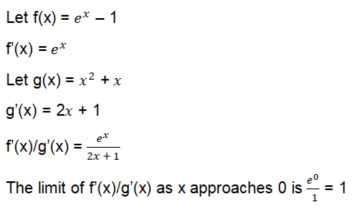
E pronto, L'Hospital vem ao resgate.

Agora, vamos voltar ao limite de Meninas Malvadas.

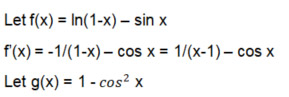
Vamos usar a regra do produto para diferenciar g(x): Lembre-se que ela diz (r(x) * s(x))' = r(x)*s'(x) + r'(x)*s(x).

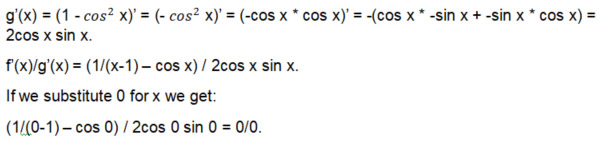
Então, L'Hospital não ajudou com o problema das Meninas Malvadas. Já que ainda ficamos com o placar sem sentido de 0 a 0, podemos afirmar com segurança que "não há limites". Na cena, Cady estava certa e seu time merecidamente venceu a competição.

jpg" />

Gostaria de dar todo o crédito a Tina Fey, roteirista principal do filme, por ter acertado os cálculos! Isso não é algo que se deva considerar trivial. Como vimos em Gênio Indomável, até mesmo os filmes mais sofisticados e com alto orçamento podem cometer erros matemáticos e científicos que me arrepiam.