Demonstração da Fórmula de Pitágoras

Esta semana, demonstrarei o clássico teorema de Pitágoras, que afirma que, em um triângulo retângulo, a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa. O exemplo mais famoso é o triângulo retângulo de lados 3, 4 e 5. Observe que ^3² + ^4² = ^5² . No entanto, antes de chegarmos a isso, apresento o nosso habitual enigma lógico semanal.

Quebra-cabeça lógico

Um filósofo antigo e distraído esqueceu-se de dar corda ao seu grande relógio de parede. Ele não tinha rádio, televisão, telefone, internet ou qualquer outro meio de ver as horas. Então, caminhou até a casa de um amigo, a alguns quilômetros de distância, por uma estrada reta no deserto. Passou a noite na casa do amigo e, quando voltou para casa, sabia como acertar o relógio. Como ele sabia?

A resposta está no final do boletim informativo.

Demonstração da Fórmula de Pitágoras

Considere o seguinte diagrama, que consiste em um quadrado grande dividido em quatro triângulos retângulos iguais e um quadrado menor no meio. Haverá um quadrado no meio porque a soma dos ângulos internos de qualquer triângulo é 180 graus. Eu demonstrei isso no boletim informativo de 13 de novembro de 2025 .

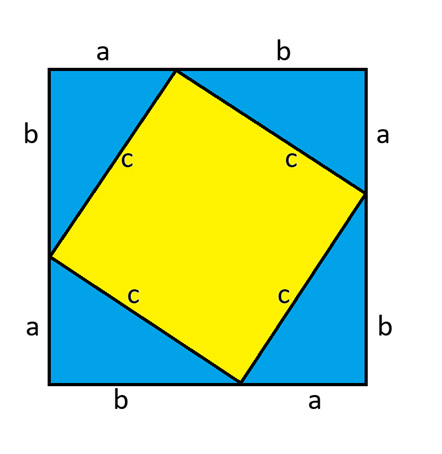
A área do quadrado maior é (a+b) ^² . A área de cada triângulo é ab² . A área do quadrado amarelo no meio é ^c² . Igualando a área do quadrado maior à soma das áreas das partes internas, obtemos:

6; família de fontes: 'Open Sans', sans-serif; cor: #313131 !important;">(a+b) ² = 4 ab 2 + c ²

^a² + 2ab + ^b² = 2ab + ^c²

Subtraindo 2ab de ambos os lados, obtemos:

^a² + ^b² = ^c²

Solução de quebra-cabeça lógico

1. O professor deu corda no relógio e o ajustou para uma hora qualquer.
2. Ao chegar à casa do amigo, ele anota a hora de chegada.
3. Ao sair, ele anota a hora em que partiu e calcula o tempo gasto na casa do amigo, subtraindo a hora de chegada da hora de partida.
4. Ele tem o cuidado de caminhar na mesma velocidade na volta que caminhou na ida à casa do amigo.
5. Ao chegar em casa, seu relógio terá adiantado o tempo gasto na casa do amigo mais o tempo de caminhada. Ele pode calcular o tempo de caminhada subtraindo o tempo na casa do amigo do tempo total. Em seguida, pode calcular o tempo de ida dividindo o tempo total de caminhada por 2.
6. Ele pode então ajustar seu relógio para a hora em que saiu da casa do amigo mais o tempo de caminhada de ida.

Vejamos um exemplo.

O relógio errado é dado corda e ajustado para 12:00. No horário correto, 8:00, ele chega à casa do amigo. À 1:00, ele sai, lembrando-se da visita de cinco horas. Quando retorna, vê que seu relógio marca 8:00. Subtraindo as cinco horas da visita, isso significa que ele passou três horas caminhando no total. Ou seja, 1,5 hora em cada sentido. Se ele saiu às 1:00 e caminhou por 1,5 hora, agora devem ser 2:30, horário para o qual ele ajusta seu relógio.