Prova de que a Série Harmônica Diverge

A demonstração desta semana será a de que a série harmônica converge. No entanto, antes de chegarmos a isso, apresento o nosso habitual enigma lógico semanal.

Quebra-cabeça lógico

Na segunda-feira, havia dois bebês na maternidade de um hospital, um menino e uma menina.

Na terça-feira, nasceu um novo bebê.

Na quarta-feira, um bebê é escolhido aleatoriamente. É um menino.

Qual a probabilidade de o bebê nascido na terça-feira ser um menino?

Prova de que a Série Harmônica Diverge

A série harmônica é o conjunto dos inversos de todos os números inteiros. Em outras palavras, 1 1 , 1 2 , 1 3 , 1 4 ,6; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 5 ,…, 1 ∞ . Diz-se que uma série é divergente se a soma de todos os seus membros for infinita. Isso não é óbvio no caso da série harmônica, porque os membros crescem infinitamente pequenos. No entanto, deixe-me provar que a soma é de fato infinita.

Método 1: O Teste de Comparação

Se eu puder provar que outra série com o mesmo número de membros ou em menor número é divergente, então a série harmônica também deve ser divergente.

Série harmônica: 1 1 , 1 2 , 1 3 , 1 4 , 1 5 , 1 6 ,6; família de fontes: 'Open Sans', sans-serif; cor: #313131 !important;"> 1 7 , 1 8 , 1 9 , 1 10 , 1 11 , 1 12 , 1 13 ,…, 1 ∞ .

Série 2: 1 1 , 1 2 ,6; família de fontes: 'Open Sans', sans-serif; cor: #313131 !important;"> 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 8 , 1 16 , 1 16 , 1 16 , 1 16 , 1 16 ,6; família de fontes: 'Open Sans', sans-serif; cor: #313131 !important;"> 1 16 , 1 16 , 1 16 , 1 32 ,…, 1 ∞ .

A Série 2 começa com os mesmos dois membros da Série Harmônica. Então, para todo n ≥ 2, ela se repete 1/2 ⁿ x 2 ^n-1 vezes. Observe que cada membro da Série 2 é igual ou menor que o da Série Harmônica. A Série 2 pode ser dividida em grupos cuja soma é 1/2 ⁿ x 2 ^n-1 = 1/2 . Para ilustrar, vou atribuir uma cor diferente a cada grupo:

Série 2: 1 1 ,6; família de fontes: 'Open Sans', sans-serif; cor: #313131 !important;"> 1 2 , 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 8 , 1 16 , 1 16 , 1 16 , 1 16 ,6; família de fontes: 'Open Sans', sans-serif; cor: #00A0D1 !important;"> 1 16 , 1 16 , 1 16 , 1 16 , 1 32 (16 vezes), 1 64 (32 vezes) …, 1 ∞

1 + ( 1 2 X ∞)= ∞

Método 2: Cálculo

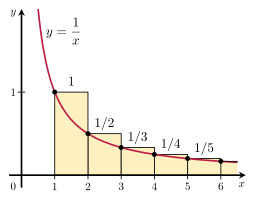
Observe que a área dos retângulos amarelos é maior que a área sob a curva vermelha. Essa área na curva vermelha é:

∫ ₁ ^∞ 1 x dx = ln(x) + c de 1 a ∞ = ln(∞) + c – ln(1) – c = ∞.

Solução de quebra-cabeça lógico

Resposta curta

Existem duas explicações possíveis para o que aconteceu. Vamos chamá-las de X e Y.

X = Menino adicionado na terça-feira e um menino é observado na quarta-feira. A probabilidade disso é (1/2)*(2/3) = 2/6 = 1/3.

Y = Menina adicionada na terça-feira e menino observado na quarta-feira. A probabilidade disso é (1/2)*(1/3) = 1/6.

X + Y = 1/3 + 1/6 = 1/2

A pergunta é qual a probabilidade dos dois eventos, sendo X o que aconteceu. Isso seria X/(X+Y) = (1/3)/(1/2) = 2/3.

Resposta longa

A fórmula da probabilidade condicional Bayesiana afirma que Prob(A dado B) = Prob(A e B)/Prob(B), onde prob(x) = probabilidade de qualquer evento x. Vamos considerar:

A = Menino adicionado na terça-feira

6; família de fontes: 'Open Sans', sem serifa; cor: #313131 !importante; ">B = Menino observado na quarta-feira

Nesse caso:

Prob(A dado B) = Prob(Menino adicionado na terça-feira dado menino observado na quarta-feira) = Prob(Menino adicionado na terça-feira e menino observado na quarta-feira)/Prob(Menino observado na quarta-feira).

Sem informações sobre o sorteio de terça-feira, há 50% de chance de um menino ter sido adicionado na terça-feira. Supondo que o bebê de terça-feira seja um menino, haveria 2/3 de chance de o bebê sorteado na quarta-feira também ser um menino.

Da mesma forma, sem informações sobre o sorteio de terça-feira, há 50% de chance de uma menina ter sido adicionada na terça-feira. Supondo que o bebê de terça-feira seja uma menina, haveria 1/3 de chance de o bebê sorteado na quarta-feira ser um menino.

A probabilidade de um menino ter sido sorteado na quarta-feira é igual a prob(menino adicionado na terça-feira)*prob(menino sorteado na quarta-feira) + prob(menina adicionada na terça-feira)*prob(menino sorteado na quarta-feira) = (1/2)*(2/3) + (1/2)*(1/3) = 1/2.

A probabilidade de um menino ser adicionado na terça-feira e um menino ser sorteado na quarta-feira = (1/2)*(2/3) = 1/3.

Portanto, a resposta é (1/3)/(1/2) = 2/3.