Agendamento Round Robin

O tema desta semana será como organizar um torneio de todos contra todos. Antes de prosseguir, um torneio de todos contra todos é um formato em que todos os jogadores enfrentam todos os outros. Em um torneio com n jogadores, o número de partidas será n(n-1)/2.

Seria fácil listar todos os n(n-1)/2 possíveis pares entre n jogadores. No entanto, o ideal é fazer isso em rodadas, onde cada jogador joga uma vez em cada rodada. Veja como fazer isso com um número par de jogadores. Vamos usar a situação com oito jogadores como exemplo. Na imagem a seguir, rotulamos os jogadores de A a H e mostramos os dois jogadores em uma partida nos quatro retângulos. Essas quatro partidas constituirão a primeira rodada. Observe como cada jogador joga.

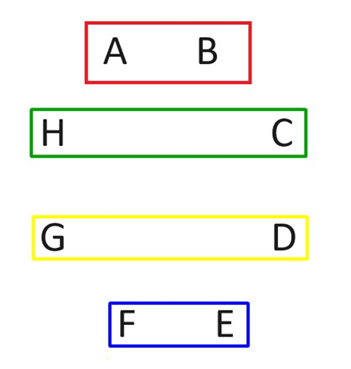
Na segunda rodada, mantenha o jogador A na mesma posição. Em seguida, gire todos os outros no sentido horário, conforme mostrado no diagrama a seguir.

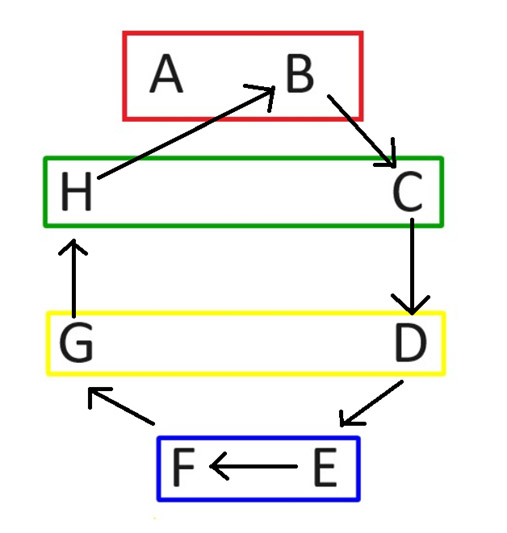
Após a rotação, a segunda rodada de partidas terá o seguinte formato:

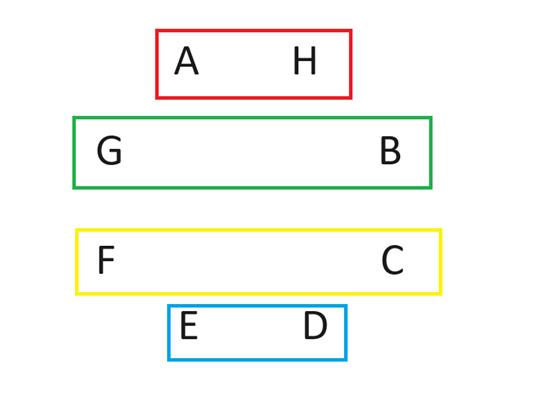
Continue fazendo isso até que todos tenham jogado contra o jogador A. Não sei explicar por que isso funciona, mas funciona. Funciona para qualquer número par de jogadores. Para mais informações sobre o assunto, pesquise por "método do círculo" e "todos contra todos".

A tabela a seguir mostra todos os confrontos no caso de oito jogadores. Observe como cada jogador enfrenta todos os outros exatamente uma vez.

Redondo	Jogador 1	Jogador 2
1	UM	B
1	H	C
1	G	D
1	F	E
1	UM	H
2	G	B
2	F	C
2	E	D
3	UM	G
3	F	H
3	E	B
3	D	C
4	UM	F
4	E	G
4	D	H
4	C	B
5	UM	E
5	D	F
5	C	G
5	B	H
6	UM	D
6	C	E
6	B	F
6	H	G
7	UM	C
7	B	D
7	H	E
7	G	F

Para um número ímpar de jogadores, basta adicionar um jogador fictício ao torneio para obter um número par. Quem jogar contra o jogador fictício passa direto para a próxima rodada, ou seja, não joga. Assim, todos terão uma rodada em que ficarão de fora. Veja como isso funcionaria em um torneio com sete jogadores.

Redondo	Jogador 1	Jogador 2
1	UM	B
1	tchau	C
1	G	D
1	F	E
2	UM	tchau
2	G	B
2	F	C
2	E	D
3	UM	G
3	F	tchau
3	E	B
3	D	C
4	UM	F
4	E	G
4	D	tchau
4	C	B
5	UM	E
5	D	F
5	C	G
5	B	tchau
6	UM	D
6	C	E
6	B	F
6	tchau	G
7	UM	C
7	B	D
7	tchau	E
7	G	F

Por fim, suponha que este seja um torneio de tênis onde cada quadra tem um lado bom e um lado ruim. O lado ruim provavelmente estaria voltado para o sol. Qual seria uma maneira justa de garantir que cada jogador jogue nos lados bom e ruim o mesmo número de vezes?

Para resolver esse problema, proponho o uso da " Expansão do Spock Lagarto ", conforme explicado na série The Big Bang Theory. Esse método de jogar pedra-papel-tesoura funciona com qualquer número ímpar de símbolos. Para determinar de forma justa qual jogador fica com o lado bom, considere o caso de sete jogadores. O diagrama a seguir mostra qual jogador fica com o lado bom, indicado pela seta apontando para o jogador que fica com o lado ruim.

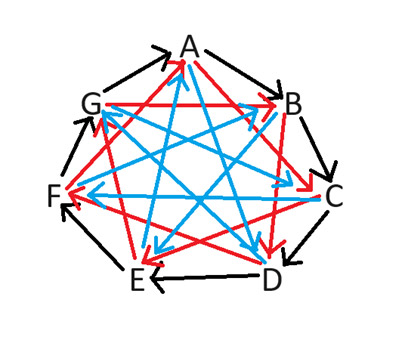
Por exemplo, se os jogadores B e D jogassem, B ficaria com o lado bom, porque a seta entre eles aponta para D. Não é difícil ver como desenhei o diagrama. As setas sempre apontam no sentido horário. É preciso desenhá-las para cada número possível de espaços de 1 a 3.

No entanto, não é necessário desenhar um diagrama desse tipo, basta um círculo de letras. Considere as duas maneiras de percorrer o círculo no sentido horário para ir de um jogador ao outro. O caminho com menos passos garante o lado bom. Considere um jogo entre B e F. No sentido horário, são quatro passos de B para 4 e três passos de F para B. Como três é menor que quatro, F fica com o lado bom.

A tabela a seguir mostra todos os confrontos possíveis em um torneio de todos contra todos com sete jogadores, incluindo quais jogadores ficam com os lados bons e ruins.

Redondo	Lado bom	Lado ruim
1	UM	B
1	C	tchau
1	D	G
1	E	F
2	UM	tchau
2	G	B
2	C	F
2	D	E
3	G	UM
3	F	tchau
3	B	E
3	C	D
4	F	UM
4	E	G
4	D	tchau
4	B	C
5	E	UM
5	D	F
5	G	C
5	B	tchau
6	UM	D
6	C	E
6	F	B
6	G	tchau
7	UM	C
7	B	D
7	E	tchau
7	F	G

Infelizmente, essa estratégia de equilíbrio lateral não funciona para um número par de jogadores. Isso ocorre porque as duas distâncias são iguais ao redor do círculo quando os dois jogadores estão em lados exatamente opostos. Se necessário, seria possível usar esse método para todos os outros confrontos, mas os jogadores teriam que ser escolhidos aleatoriamente quando estivessem a 180 graus de distância um do outro no círculo.

Por ora, não abordarei mais esse assunto. Reservo-me o direito de expandi-lo em um boletim informativo futuro. Possíveis tópicos para discussão futura incluem partidas com três ou mais jogadores, bem como o uso de múltiplas quadras, onde se deseja equilibrar a frequência com que cada jogador utiliza cada uma delas.

Para finalizar, desejo a todos um feliz Hanukkah!

Escrito por: Michael Shackleford