Teorema da Soma dos Ângulos Internos de um Triângulo: 180 Graus

É sabido que a soma dos ângulos internos de qualquer triângulo é 180 graus. Nesta newsletter, apresentarei uma demonstração simples. No entanto, antes disso, apresento o nosso habitual enigma lógico semanal.

Quebra-cabeça lógico

Um rei possui 49 moedas de ouro. Cada moeda pesa 1, 2, 3, ... 49 gramas. Como ele pode dividi-las entre seus sete filhos de modo que cada filho receba sete moedas e a soma dos pesos seja igual?

Demonstração de que a soma dos ângulos internos de qualquer triângulo é igual a 180 graus.

Vou começar desenhando um triângulo qualquer e identificando seus ângulos.

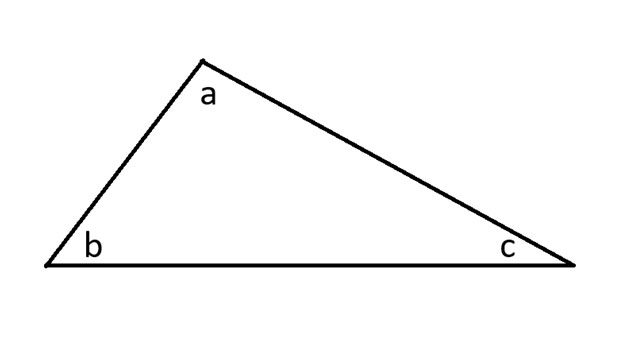
Em seguida, vou estender todos os três lados do triângulo e também traçar uma linha paralela que toque o ângulo a.

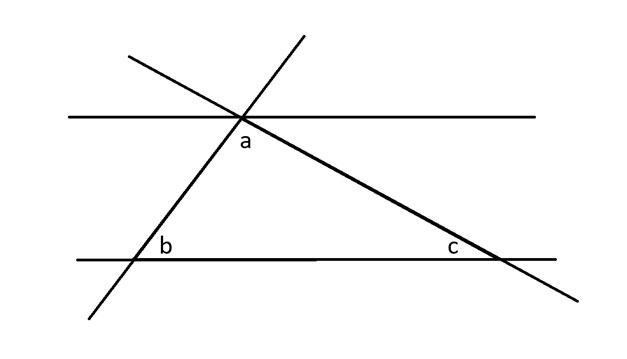
Em seguida, aplicarei o teorema dos ângulos opostos ao ângulo b, que afirma que os ângulos nos vértices opostos de duas retas concorrentes são iguais.

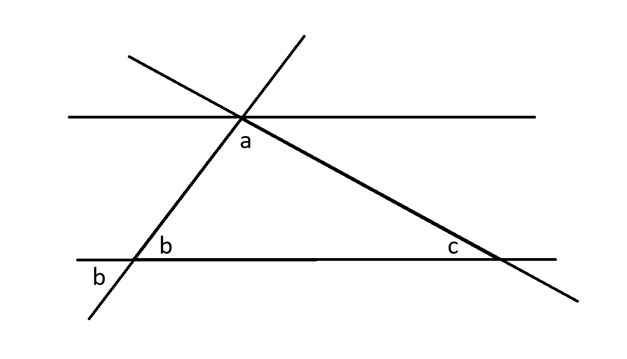
Quando uma diagonal intercepta um conjunto de retas paralelas, ela cria os mesmos ângulos nos pontos de interseção com cada reta. Aplico esse princípio para mostrar outro ângulo de b graus ao lado do ângulo a. Em seguida, faço o mesmo com o ângulo c.

6; família de fontes: 'Open Sans', sem serifa; cor: #313131 !importante; ">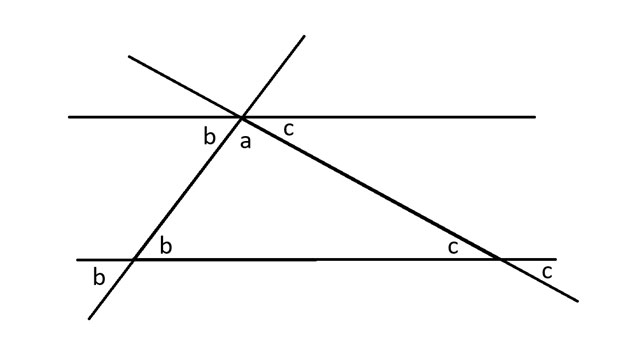

Um círculo tem 360 graus. Portanto, uma semicircunferência tem 180 graus. Em outras palavras, observando os ângulos na base da reta paralela superior, a + b + c = 180 graus. Esses são também os três ângulos do triângulo original. Assim, a soma dos ângulos internos de um triângulo é igual a 180 graus.

Solução de quebra-cabeça lógico

Crie um quadrado mágico e dê a cada filho as moedas de uma coluna qualquer. Você também pode dividir as moedas por linhas. "Como se faz um quadrado mágico 7x7?", você pode perguntar. O método a seguir é conhecido como Método Siamês e foi descoberto na Índia há muito tempo.

Vamos começar com uma grade com as mesmas dimensões de um tabuleiro de Batalha Naval 7x7.

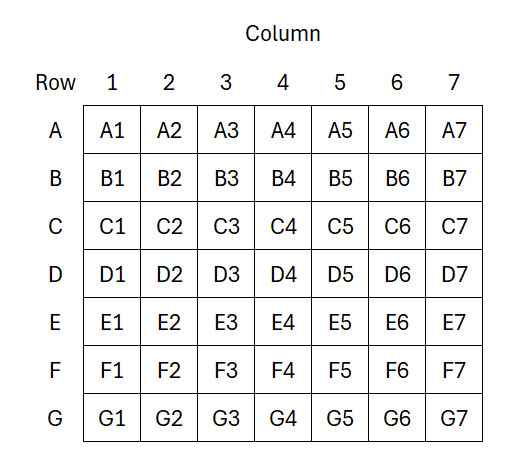
Comece com o número 1 na célula A4. Em seguida, siga estas regras:

1. Para a próxima posição, sempre adicione 1 ao número anterior.
2. Siga sempre na direção noroeste, a menos que esse espaço esteja ocupado ou que você já esteja na linha A ou na coluna 7.
3. Se você estiver na linha A, passe para a coluna G para o próximo número.
4. Se você estiver na coluna 7, volte para a coluna 1 para o próximo número.
5. A chamada A7 será redirecionada em ambas as direções para G1.
6. Se a próxima casa para onde você deve ir estiver ocupada, então desça para a casa seguinte correspondente ao próximo número (ela deve estar vazia).

Eis como começamos:

1. 1 na célula A4.
2. Estamos na linha A, então vamos para a linha G, colocando um 2 na célula G5.
3. Em seguida, colocamos um 3 em F6 e um 4 em E7.
4. Estamos na coluna 7, então damos a volta, colocando um 5 em D1.
5. Coloque um 6 em C2 e um 7 em B3.
6. Em seguida, chegaríamos à letra A4, mas ela está ocupada com o número 1. Então, descemos e colocamos o próximo número, um 8, na letra C3.
7. Continue repetindo até que o Quadrado Mágico esteja completo.

Eis como ficará quando estiver concluído:

jpg" />

Este método funciona para qualquer quadrado mágico de dimensões ímpares.

Em seguida, decida se você vai dividir por linhas ou colunas. Cada filho receberá as moedas encontradas em uma das linhas/colunas. Por exemplo, se você optar por colunas, o filho 1 receberia as moedas de número 30, 38, 46, 5, 13, 21 e 22.