Demonstração da Soma dos N Primeiros Números Inteiros

Esta semana, apresento uma das minhas demonstrações mais fáceis: 1 + 2 + 3 + ... + n = n(n + 1)/2. Mostro-a de duas maneiras muito intuitivas. É a minha demonstração mais fácil até agora. No entanto, antes de chegarmos a isso, apresento o meu habitual enigma lógico semanal.

Quebra-cabeça lógico

Alice, Bob e Cole fazem as seguintes declarações:

1. • Alice: Bob é um mentiroso.
2. • Bob: Cole é um mentiroso.
3. • Cole: Alice e Bob são mentirosos.

Os três ou sempre dizem a verdade ou sempre mentem. Todos eles sabem se os outros dois estão falando a verdade. Quem está dizendo a verdade?

Veja a resposta e a solução no final do boletim informativo.

Demonstração da Soma dos N Primeiros Números Inteiros

Todos deveriam saber que a soma dos primeiros n inteiros é n(n+1)/2. Em outras palavras, 1+2+3+…+n = n(n+1)/2. Apresento duas demonstrações simples que comprovam essa afirmação.

Método 1

É fácil ver que o número médio na sequência é (n+1)/2. O número de termos na série é n. A soma é igual ao produto do número de termos e o termo médio = n × (n+1)/2 = n(n+1)/2.

Este mesmo método pode ser usado para encontrar a soma com quaisquer pontos inicial e final. Vamos chamar o número inicial de a e o número final de b. A média será (a+b)/2. O número de termos será (a-b+1).Portanto, a soma de todos os números da série será (a-b+1) × (a+b)/2.

Método 2

O próximo método é mais fácil de explicar visualmente. Considere o diagrama a seguir, onde os quadrados azuis ilustram os números inteiros de 1 a 5.

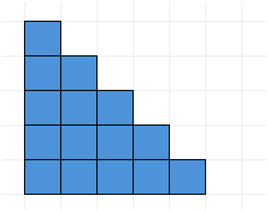
Em seguida, duplique-a e coloque-a ao lado da peça original, formando um retângulo.

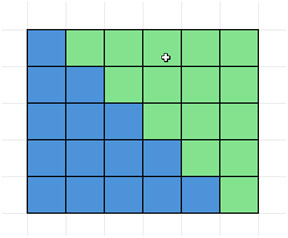
Observe que as dimensões do retângulo acima são 5 × 6. No caso geral da soma dos números inteiros de 1 a n, as dimensões são n × (n+1). Divida essa área por 2, pois buscamos a área de apenas uma das duas partes. Portanto, a área de uma única parte é n(n+1)/2.

Solução de quebra-cabeça lógico

As três pessoas têm dois estados possíveis: falando a verdade ou mentindo. Isso resulta em ^2³ = 8 possibilidades. Listei todas elas na tabela abaixo.

Cenário	1	2	3	4	5	6	7	8
Alice	T	T	T	T	F	F	F	F
Prumo	T	T	F	F	T	T	F	F
Cole	T	F	T	F	T	F	T	F

Note que Bob e Cole se chamam de mentirosos. A única maneira disso ser possível é se um deles estiver dizendo a verdade e o outro estiver mentindo. Portanto, podemos eliminar as quatro situações em que Bob e Cole compartilham o mesmo nível de sinceridade. Restam, então, os cenários 2, 3, 6 e 7. Vamos analisá-los um de cada vez.

No cenário 2, presume-se que Alice esteja dizendo a verdade. Sua declaração verdadeira torna Bob um mentiroso. No entanto, Bob também está dizendo a verdade neste cenário, o que leva a uma contradição. Portanto, o cenário 2 está descartado.

No cenário 3, presume-se que Alice seja sincera. Ela diz que Bob é um mentiroso, o que é verdade de acordo com as premissas do cenário 3. No entanto, Cole é descrito como alguém que diz a verdade, e ele afirma que Alice está mentindo. Alice não pode ser sincera e mentirosa ao mesmo tempo, portanto, o cenário 3 está descartado.

No cenário 7, é dado que Alice está mentindo. Ela diz que Bob é um mentiroso, o que é verdade. No entanto, isso faria com que Alice dissesse a verdade. Alice não pode dizer a verdade e mentir ao mesmo tempo, então o cenário 7 está descartado.

Isso nos deixa apenas com o cenário 6. Vamos verificar se ele funciona. Se Alice fosse mentirosa, isso tornaria Bob sincero. Se Bob fosse sincero, então Alice ou Bob, ou ambos, seriam sinceros. Bob é sincero, então a afirmação de Cole é falsa. Portanto, faz sentido. Bob é a única pessoa sincera.