Análise de pares quadrados - Aposta paralela no Blackjack

Olá, aqui é o Mike. O objetivo deste vídeo é mostrar como calcular o retorno ao jogador (RTP) da aposta paralela Pair Square no Blackjack . Antes de explicar a aposta "Bet the Set", também conhecida como Pair Square, deixe-me revisar rapidamente algumas funções matemáticas que você talvez já conheça. O fatorial de n representa o número de maneiras diferentes de organizar n itens únicos.

É simplesmente o produto de todos os números inteiros de um até n .

Por exemplo:

O fatorial de cinco seria o número de maneiras de organizar cinco itens diferentes, que seria 1×2×3×4×5, ou seja, 120. Deixe-me também explicar a função de combinação. Ela representa o número de maneiras de escolher Y itens dentre X, neste exemplo específico, sem levar em consideração a ordem.

Por exemplo, o número de maneiras pelas quais você poderia escolher três acompanhamentos diferentes dentre oito opções no El Pollo Loco.

Esta função...

...é igual a X fatorial dividido por Y fatorial, dividido por X menos Y fatorial. Expliquei por que isso é verdade no meu vídeo sobre probabilidades no pôquer. Um exemplo disso seria: de quantas maneiras você pode escolher cinco cartas dentre 52?

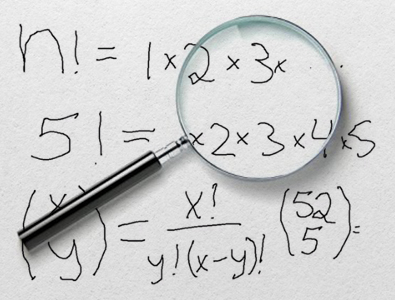
Isso é igual a 52 fatorial dividido por cinco fatorial dividido por 47 fatorial, o que resulta em 2.598.960. Feito esse ajuste, vamos à segunda parte, onde calculo as combinações de cada resultado possível da aposta Pair Square.

Pronto para passar para a próxima etapa?

O objetivo é calcular o número de combinações de cada resultado possível dessa aposta. Esse é o ponto crucial de todo o vídeo . Vamos supor seis baralhos de cartas. Para o par de cartas do mesmo naipe, há 52 cartas diferentes no sapato. Treze valores vezes quatro naipes é igual a 52. Elas devem ser iguais.

Por exemplo, ambas devem ser o cinco de ouros. Depois de escolher a carta específica, há seis dessas cartas no sapato de seis baralhos .

Você deve escolher duas dessas seis. Seis escolhem duas, o que dá 15, então 52 vezes 15 é igual a 780. Existem 780 maneiras de você conseguir a vitória com um par do mesmo naipe. Quantas maneiras existem de se ter um par de naipes diferentes? Bem, primeiro, você precisa escolher o valor do seu par de naipes diferentes, por exemplo, cincos.

Então você deve escolher dois naipes diferentes para esse par, porque eles precisam ser diferentes. Se fossem iguais, você teria um par de naipes e ganharia mais dinheiro.

Existem quatro maneiras de escolher dois naipes dentre as quatro, o que resulta em seis. Então, depois de escolher seu valor e seus dois naipes, existem seis maneiras de escolher cada um deles dentre os seis baralhos do sapato.

Por exemplo:

Se suas duas cartas fossem o Rei de Paus e o Rei de Espadas, haveria seis de cada um deles no sapato de seis baralhos. Treze vezes seis vezes seis ao quadrado é igual a 2.808. Por fim, a maneira de perder esta aposta é não conseguir um par.

De quantas maneiras você pode não conseguir um par?

Bem, você terá que escolher duas figuras diferentes dentre as 13 disponíveis, por exemplo, sete e dez. Depois de escolher suas duas figuras específicas, haverá 24 cartas de cada uma dessas figuras em todo o baralho.

Como cada baralho tem quatro cartas de um valor específico e há seis baralhos no total, existem, por exemplo, 24 ases no total. Se os nossos dois valores fossem, digamos, ases e reis, haveria 24 ases e 24 reis.

Você escolhe um de cada um desses grupos.

13 escolhe dois, ou seja, 78 vezes 24 ao quadrado, é igual a 44.928, então essas são as nossas combinações. Em seguida, vamos transferir tudo isso para o Excel para ver que tipo de valor estamos obtendo com a aposta Pair Square.

Vamos prosseguir para a parte final...

Acabei de mostrar o número de combinações de cada resultado possível na aposta Pair Square. A tabela de pagamentos mais comum com seis baralhos é: um par do mesmo naipe paga 15 para 1 e um par de naipes diferentes paga 10 para 1.

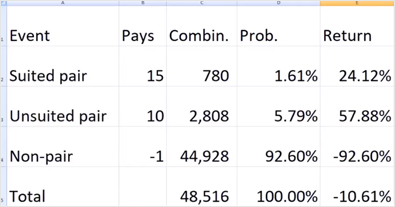
Vamos calcular a probabilidade de cada evento - o que é muito simples.A probabilidade de formar um par do mesmo naipe é o número de maneiras de formar um par do mesmo naipe dividido pelo número total de maneiras de escolher duas cartas dentre as 312 e o baralho, que é 40.516. Dividindo 780 por 40.516, obtemos aproximadamente 1,61%.

Usando a mesma fórmula do número de combinações de cada evento dividido pelo total, obtemos estas outras probabilidades: 5,79% de um par de cartas incompatíveis e 92,6% de obter duas cartas de classificação diferente.

Próximo...

...a maneira que eu gosto de analisar uma aposta é simplesmente multiplicar o ganho pela probabilidade. O retorno de um par do mesmo naipe é 15 vezes o ganho vezes a probabilidade de obtê-lo, 1,61%, o que resulta em... Vamos ampliar para você: 24,12%. Usando a mesma fórmula, vemos que o retorno de um par de cartas diferentes do mesmo naipe é de 57,88%, e o retorno de um não-par é de -92,6%.

Isso significa que se o jogador... isso é um dólar.

Por exemplo: ele pode esperar receber 24,12 centavos de volta com seus pares do mesmo naipe, 57,8 centavos com seus pares de naipes diferentes, mas perder 92,6 centavos com suas cartas que não formam pares. Para obter o valor total para o jogador , basta somar esses valores, obtendo -10,61%.

Isso significa...

O jogador pode esperar perder 10,61% de todo o dinheiro apostado no Pair Square. Outra forma de dizer isso é que a vantagem da casa é de 10,61%. Ou seja, para cada dólar apostado, o jogador pode esperar receber cerca de 89,39 centavos, e 10,61 centavos vão para o cassino.

Para colocar isso em perspectiva: a vantagem da casa no blackjack em si pode ser tão baixa quanto 0,28%. Mesmo com regras desfavoráveis, fica mais perto de 0,6%. Aqui você tem essa vantagem da casa bem abaixo de 1%, considerando que um blackjack paga três para dois. Algo que você deve tentar conseguir sempre que possível, e então essa vantagem da casa de quase 11%.

Isso só comprova o que já disse milhares de vezes: apostas paralelas são apostas para otários. Este é um exemplo perfeito disso. Recomendo que você evite esta aposta paralela, assim como todas as outras, se possível.

Obrigado por assistirem, pessoal, e nos vemos no meu próximo vídeo.

Escrito por: Michael Shackleford