Probabilidades no pôquer Five Card Stud

Olá, meu nome é Mike, e o objetivo deste vídeo é mostrar como calcular as probabilidades no pôquer de cinco cartas (Five-Card Stud) . Em outras palavras, qual é a probabilidade de formar qualquer mão de pôquer com cinco cartas aleatórias dentre 52? Antes de responder à pergunta sobre o número de combinações possíveis para cada mão de pôquer, deixe-me fazer uma pergunta mais simples. Se você souber a resposta, pode pular para a próxima parte.

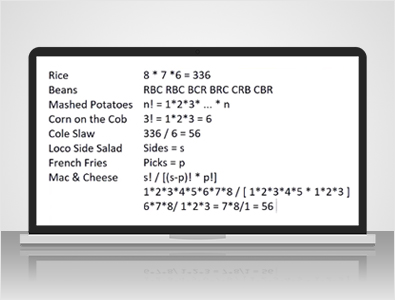
Em El Pollo Loco:

Eles têm oito acompanhamentos chamados de clássicos, que listei à esquerda. Também têm alguns acompanhamentos especiais, mas não vou entrar em detalhes. Se você pedir a refeição com 12 peças, pode escolher três desses oito acompanhamentos. Vamos supor que você precise escolher três coisas diferentes.

A questão é...

...de quantas maneiras você pode pedir três acompanhamentos diferentes dentre oito opções? Em outras palavras, digamos que você vá lá todos os dias e peça três acompanhamentos diferentes todos os dias. Quantos dias você conseguiria passar sem repetir os mesmos três acompanhamentos?

Se a ordem em que você os pediu fosse importante, a resposta seria 8 x 7 x 6, porque existem oito maneiras de escolher o primeiro item, sete maneiras de escolher o segundo e seis maneiras de escolher o terceiro, mas o caixa não se importa com a ordem em que você os pediu.

Se você disser -

"Eu quero arroz, feijão e milho." Você vai receber a mesma coisa, quer diga "arroz, feijão e milho" ou "milho, feijão e arroz". De quantas maneiras diferentes você pode pedir três acompanhamentos diferentes? Bem, digamos que você goste de arroz, feijão e milho. Você poderia pedi-los nessa ordem, poderia pedir arroz, milho e feijão, poderia pedir feijão, milho e arroz. Você poderia pedir feijão, arroz e milho, ou milho, arroz e feijão, ou milho, feijão e arroz. Então, são seis maneiras possíveis.

Como eu sabia que eram seis sem simplesmente anotá-los?

Bem, existe uma fórmula muito simples . Se houver N itens, o número de maneiras de ordená-los é 1 x 2 x 3 vezes até N.

Neste caso, a pergunta era: de quantas maneiras você pode ordenar três coisas? Bem, são 3!, que é 1 x 2 x 3, que é igual a 6. Das 336 maneiras de ordenar os três itens dentre as oito possíveis, você divide por seis porque existem seis maneiras de ordenar cada combinação, e isso resulta em 56.

Qual é a fórmula geral, você pode perguntar?

Se houver, digamos que o número de lados seja igual a S, e o número de escolhas permitidas seja P, a fórmula geral para o número de maneiras de escolher P coisas de um conjunto de S é s! / (s - p! x p!). Deixe-me mostrar que isso funciona com o exemplo.

Nesse caso:

s = 8, então 8! é 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8, e no denominador temos s - p, ou 8 - 3, que é 5 ou 5!. Então, 1 x 2 x 3 x 4 x 5, assim como p! ou 3!, que é 1 x 2 x 3. Você pode ver 1 x 2 x 3 x 4 x 5, que é igual a 120, tanto no numerador quanto no denominador, então vamos cancelar isso, ficando com 6 x 7 x 8 / 1 x 2 x 3. Bem, 2 x 3 = 6, e há um seis aparecendo tanto no numerador quanto no denominador, então vamos dividir isso.

Só nos resta...

...7 x 8 / 1, que é 56. Para os propósitos deste vídeo, deixe-me apresentar uma função. Chamaremos a função C de x e y como o número de maneiras de escolher y itens de x, ou x escolhe y, como diríamos matematicamente, e a definiremos como x! / x - y! vezes y!.

No caso do exemplo do El Pollo Loco, se a pergunta fosse:

"De quantas maneiras você pode escolher três slides dentre oito?"

Expressaríamos isso assim, o que seria igual a... a troca equivale a 56. Acho que finalmente estamos prontos para começar a falar sobre pôquer. De quantas maneiras você pode escolher cinco cartas dentre 52? Bem, seria 52 escolhe 5, que é 52! / 47!, 47 porque 52 - 5 x 5!, e isso é igual a 2.598.960. Vamos começar com um royal flush.

Bem, isso é bem simples. Existem quatro naipes para o royal flush: copas, espadas, paus e ouros.Os valores devem ser dez: Valete, Dama, Rei e Ás. Sim, só existem quatro possibilidades. Um naipe de copas, ouros, paus ou espadas.

Que tal um straight flush?

Bem, novamente, ainda temos os quatro naipes, mas a sequência de um straight flush pode começar com um Ás, ou seja, Ás, dois, três, quatro, cinco, também conhecido como straight flush "wheel", até nove, dez, Valete, Dama, Rei. Se fosse dez, Valete, Dama, Rei, Ás, então seria um royal flush. A carta mais baixa pode ser qualquer valor entre um Ás e um nove.

Nesse caso...

...o Ás vale como um. Existem nove combinações possíveis para o straight flush, então 4 naipes x 9 combinações = 36. Com a quadra, existem 13 valores possíveis para a quadra, por exemplo, Damas, e então restam 48 cartas no baralho para o singleton depois de retirar as quatro cartas da quadra. Isso é igual a 624.

Para a casa cheia

Existem 13 combinações possíveis para uma trinca e 12 combinações restantes para um par. Para a trinca, temos quatro combinações possíveis, ou seja, três maneiras de escolher três naipes dentre quatro, vezes quatro combinações possíveis, ou seja, duas maneiras de escolher dois naipes dentre quatro. Isso resulta em 13 x 12 x 4 x 6, que é igual a 3.744. Para o flush, bem, temos quatro naipes possíveis.

De quantas maneiras é possível escolher cinco cartas entre as 13 do naipe dado?

Bem, isso seria 13 escolhe 5, mas 10 dessas combinações resultariam em uma sequência de flush ou um royal flush. Por exemplo, 5, 6, 7, 8, 9 resultariam em uma sequência de flush, então temos que escolher esses 10 conjuntos de valores consecutivos. Isso nos deixa com 13 escolhe 5, que é 1.287. Subtraindo o 10 e multiplicando por 4, obtemos 5.108.

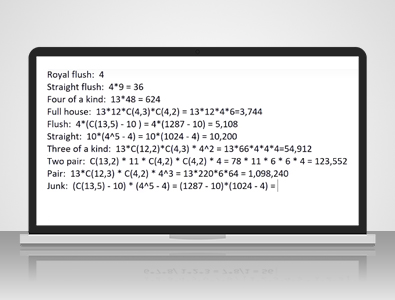
Que tal um direto?

Bem, como acabamos de ver com o flush, existem 10 combinações possíveis para a sequência, começando com Ás, dois, três, quatro, cinco e indo até 10, Valete, Dama, Rei, Ás. Para cada carta, para cada valor nessa sequência, existem quatro naipes possíveis. 4 x 4 x 4 x 4 x 4 = 4⁵, o número de maneiras de escolher um naipe diferente para cada uma das cinco cartas. Se escolhermos o mesmo naipe todas as cinco vezes, também teremos um straight flush ou royal flush. Precisamos subtrair esses. 4⁵ = 1.024 - 4 = 10.200 maneiras de formar uma sequência.

Que tal uma trinca?

Bem, existem 13 maneiras de escolher o valor da trinca, e depois você precisa escolher dois valores dentre os 12 restantes para as duas cartas individuais. Feito isso, você precisa escolher quatro dentre três naipes para a trinca, e então um naipe dentre quatro para cada uma das duas cartas individuais.

Restam-nos 13 maneiras de escolher o valor da trinca. Há 66 maneiras de escolher dois valores dentre os 12 restantes para as duas cartas individuais, vezes quatro maneiras de escolher os três naipes dentre os quatro para a trinca, e também quatro maneiras de escolher um naipe para as duas cartas individuais. A resposta é 54.912.

Que tal dois pares?

Bem, existem 13 maneiras de escolher duas cartas dentre as 13 possíveis para formar um par, e então você terá uma carta restante para a carta isolada. Para cada um dos pares, existem quatro maneiras de escolher dois naipes dentre os quatro possíveis para formar um par. Existem quatro naipes para a carta isolada. 13 maneiras de escolher duas cartas é igual a 78 vezes 6 vezes 6 vezes 4, que é igual a... esqueci minhas 11 cartas restantes para a carta isolada. 78 x 11 x 6 x 6 x 4 = 123.552.

Para o par

Existem 13 maneiras de escolher o valor do par, e depois você precisa escolher três valores dentre os doze restantes para as três cartas individuais. Para o seu par, existem quatro maneiras de escolher dois naipes dentre quatro, e para cada uma das três cartas individuais, existem quatro naipes possíveis para escolher. 4 x 4 x 4 é o número de maneiras de escolher três naipes para as três cartas individuais, o que é igual a 13 x 12 - 12 escolhe três = 220 x 6 x 4^3 = 64 = 1.098.240.

Finalmente

Vamos calcular a probabilidade de ter um Ás maior à esquerda ou menor, que chamarei de "jogo ruim". Para ter um jogo ruim, você precisa de cinco cartas de valores diferentes dentre as 13 possíveis. Existem 13 maneiras de escolher cinco cartas de valores diferentes dentre as dez possíveis, mas, como vimos com os flushes, precisamos eliminar os décimos valores que formam uma sequência. Depois de escolher suas cinco cartas de valores não consecutivos, existem quatro naipes possíveis para cada uma delas.

Você eleva quatro à quinta potência...

...E como vimos com as sequências, temos que subtrair quatro, que é o número de maneiras de escolher o mesmo naipe todas as vezes, o que resultaria em um flush. Treze escolhem cinco, que é igual a 1.287, menos 10 para as sequências, vezes quatro elevado à quinta potência, que é igual a 1.024, menos quatro, que é igual a 1.302.540.

Próximo

Vamos colocar tudo isso em uma planilha. Deixe-me mostrar rapidamente como fazer tudo isso no Excel. Já vimos que existem apenas quatro maneiras de se obter um Royal Flush, uma para cada naipe, 36 Straight Flushes, quatro naipes vezes nove combinações possíveis. Para uma Quadra, há 13 valores para escolher: quatro, a própria Quadra e 48 cartas restantes para o singleton. Para um Full House, há 13 valores para a Trinca e 12 para o Par.

Quatro escolhem três maneiras de escolher os naipes da trinca. Quatro escolhem duas maneiras de escolher dois naipes dentre quatro para o par. A maneira de expressar essa fórmula no Excel é com esta fórmula comum, combinando um número grande com uma vírgula e um número pequeno, exatamente como eu escrevi ali. Isso nos dá o 3.744 que obtivemos anteriormente.

Para a descarga

Há quatro naipes para escolher, 13 cartas para escolher de cinco maneiras, cinco valores dentre as 13 desse naipe menos 10 combinações que resultariam em um straight flush ou um royal flush por serem consecutivas. Isso nos deixa com 5.108 flushes. Para as sequências, existem 10 combinações possíveis, quatro naipes para cada carta na combinação, mas subtraindo quatro dos quatro naipes que resultariam em um straight flush ou um royal flush, chegamos a 10.200.

Para o trio de tipos

Existem 13 combinações possíveis para uma trinca, 12 combinações possíveis para escolher duas cartas de um mesmo naipe entre quatro, quatro combinações possíveis para escolher três naipes entre quatro e quatro combinações possíveis para escolher os dois naipes dos ...

Para o par, temos 13 posições para o par, 12 para escolher três posições dentre 12 para três Singletons. Quatro para escolher duas posições dentre quatro para o par e quatro elevado ao cubo para as maneiras de escolher três posições dentre três Singletons.

Finalmente, para o lixo

Existem 13 maneiras de escolher cinco cartas de um total de 13, menos as 10 maneiras consecutivas que resultariam em uma sequência, e quatro maneiras de escolher cada um dos naipes. Quatro elevado à quinta potência menos quatro são as maneiras de se obter um flush. Como você pode ver, a soma de tudo isso é 2.598.960, o mesmo resultado que obtivemos no início deste vídeo. Ok, vamos para uma aplicação prática disso tudo.

Um dos centenas de jogos de cassino que eu abordo no meu site Wizard of Odds , aqui, se chama : Let it ride .

Vamos abrir essa página. É um jogo de pôquer baseado em uma mão de cinco cartas, sem sorteio. Tudo depende de cinco cartas aleatórias dentre 52. Não vou explicar todas as regras, mas existe uma aposta paralela que paga com base no valor das suas cinco cartas.

Você pode ver...

...listei nove dessas tabelas de pagamento possíveis aqui, mas a tabela quatro é bastante comum. Eu já a transcrevi para esta tabela aqui; a aposta custa $1. Se você conseguir um Royal Flush, ganha $20.000; um Straight Flush, $20.000; e uma Quadra, $400. Esses pagamentos, aliás, são de 4 para 1, o que significa que você não fica com sua aposta original se ganhar.

Aqui estão todas as combinações cujas probabilidades eu já calculei, e esta coluna de retorno aqui é o produto da vitória pela probabilidade.

Por exemplo, existe:

Como já sabemos, a probabilidade de se obter um Royal Flush é de aproximadamente quatro milhões e vinte e seiscentos mil. Se multiplicarmos essa probabilidade por 20.000, obtemos um retorno esperado de 3,08 centavos. Esse é o valor que o jogador pode esperar receber de volta, caso aposte um dólar, em forma de ganhos com um Royal Flush. Ele pode esperar receber 2,77 centavos de volta por um Straight Flush, e assim por diante.

Fazendo as contas, a conclusão é que, para um jogador, uma aposta de US$ 1 rende cerca de 74,4667 centavos. Em outras palavras, para esse dólar, o jogador pode esperar receber aproximadamente 74 centavos.47% e o cassino ficará com 25,53%.

A forma como eu expressaria isso...

... a vantagem da casa é de 25,53%, então pense nisso por um minuto. O cassino fica com mais de 25% dessa aposta, o que só comprova o que venho dizendo há mais de 20 anos: apostas paralelas são todas apostas furadas. Se você aprender apenas uma coisa com este vídeo, espero que seja isso. Ele já está longo o suficiente, peço desculpas pela duração e espero que tenha sido informativo e que você tenha aprendido algo.

Obrigado por assistir.

Escrito por: Michael Shackleford