Vídeo sobre a probabilidade de um bracket perfeito

Olá, meu nome é Mike, e este vídeo tentará responder à pergunta: Qual a probabilidade de preencher perfeitamente o palpite do torneio March Madness?

Vou partir do princípio de que você já tem algum conhecimento básico sobre como funciona , mas, resumidamente, há 64 times de basquete competindo em um torneio de eliminação simples; isso significa que haverá um total de 63 jogos.

Eles dividem o torneio em quatro divisões e, em cada divisão, na primeira rodada, o time cabeça de chave número 1 joga contra o time cabeça de chave número 16, o cabeça de chave número 2 joga contra o número 15, o número 3 joga contra o número 14 e assim por diante. Depois, os vencedores de todos os jogos da primeira rodada se enfrentam na segunda rodada, e, no final, apenas um time é definido como campeão.

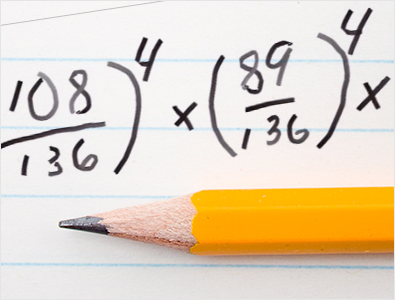
Agora, todo mês de março...

...sempre surge na mídia a questão da probabilidade de preencher um palpite perfeito, e me arrepio só de ouvir o número: 1 em 9 quintilhões, 223 quatrilhões, 372 trilhões, 36 bilhões, 854 milhões e 781 mil; acredito. Essa é simplesmente a probabilidade de acertar 63 lançamentos de moeda seguidos. Não acho que alguém preencha um palpite do March Madness dessa forma, porque alguns times são obviamente melhores que outros. Por exemplo, o time cabeça de chave número 1 é obviamente melhor que o cabeça de chave número 16.

Antes de prosseguir...

...deixe-me dizer que este vídeo foi gravado em abril de 2018, então é baseado em todos os jogos do March Madness disputados de 1985 a 2018. Ok, eu também queria comentar outro vídeo no YouTube de um professor, Jeff Bergen . Ele diz que, com alguma estratégia que ele não detalha, a probabilidade de um palpite perfeito é de 1 em 128 bilhões. Esse número é bem próximo do que eu encontrei.

Eu desafiaria o Professor Bergen a explicar como ele chegou a esse número, mas vou explicar como cheguei ao meu. Bem, minha estratégia é muito simples. Você sempre escolhe o time com a melhor classificação em todos os jogos e, eventualmente, restarão apenas quatro times cabeças de chave número 1, caso em que você pode escolher aleatoriamente.

Antes que alguém escreva nos comentários

Deixe-me dizer que você pode melhorar ainda mais isso analisando as probabilidades atuais dos jogos e, por exemplo, quando se trata de um confronto entre o cabeça de chave número 1 e o cabeça de chave número 1, você pode consultar as probabilidades de Las Vegas para ver qual time tem a melhor chance de vencer, mas não vou entrar nesse assunto.

Este vídeo vai se basear simplesmente em escolher o time com a melhor classificação em todas as partidas e, quando chegar a hora de escolher entre os quatro times com a melhor classificação, a escolha será aleatória. Ok, isso é tudo que eu preciso dizer para a introdução.

Peço desculpas antecipadamente, pois na próxima parte deste vídeo usarei um tablet. Já tive muitos problemas técnicos para fazê-lo funcionar corretamente, então achei melhor gravar a introdução desta forma. Sem mais delongas, aqui está como calcular a probabilidade de um palpite perfeito no torneio March Madness, considerando a estratégia que acabei de mencionar.

Muito bem, vamos lá:

Este é o meu primeiro vídeo feito com uma mesa digitalizadora criativa, se é que esse é o termo correto. Sempre quis fazer vídeos no estilo da Khan Academy, mas sobre jogos de azar e matemática. Feita a introdução, vamos direto aos cálculos.

A probabilidade de um time cabeça de chave número 1 vencer um time cabeça de chave número 16, eu estimo em 135 de 136, porque até agora, houve 136 jogos desse tipo e o cabeça de chave número 1 venceu 135 vezes. Essa é a probabilidade de o cabeça de chave número 1 vencer qualquer jogo específico, que é de 99,26%.

No entanto...

...existem quatro divisões diferentes, então você precisa alcançar isso quatro vezes, ou seja, eleve isso à quarta potência.

Agora, também existem quatro jogos diferentes em que o segundo colocado enfrenta o décimo quinto. Das 136 vezes em que isso aconteceu, o segundo colocado venceu 127. A probabilidade, novamente, considerando os dados históricos, de um segundo colocado vencer um décimo quinto é de 93,38%, e isso precisa acontecer quatro vezes, considerando as quatro divisões diferentes.

Da mesma forma, a probabilidade de um time cabeça de chave número 3 vencer um time cabeça de chave número 14 é 115 dividido por 136, e novamente, você precisa fazer esse cálculo quatro vezes. Já a probabilidade de um time cabeça de chave número 4 vencer um time cabeça de chave número 13 é 108 dividido por 136, e novamente, eleve esse valor à quarta potência para os quatro jogos que você precisa vencer.

A probabilidade de um time cabeça de chave número 5 vencer um cabeça de chave número 12 é de 89 em 136, o que equivale a cerca de 65,44% elevado à quarta potência. A probabilidade de um time cabeça de chave número 6 vencer um cabeça de chave número 11 é de 85 em 136, o que, para qualquer partida específica, corresponde a 62,5%. A probabilidade de um time cabeça de chave número 7 vencer um cabeça de chave número 10 é de 83 em 136. A probabilidade de cada partida ser vencida é de 61,03%. Finalmente, a probabilidade de um time cabeça de chave número 8 vencer um cabeça de chave número 9 é de 71 em 136, e, novamente, esse cálculo precisa ser feito quatro vezes.

Se você ganhar todos esses jogos...

...você avançará da primeira rodada. Então, na segunda rodada, os cabeças de chave número 1 jogarão contra os cabeças de chave número 8. Isso já aconteceu 72 vezes, e dessas 72 vezes, o cabeça de chave número 1 venceu o cabeça de chave número 8 em 58 ocasiões. A probabilidade de um cabeça de chave número 1 vencer um cabeça de chave número 8 é de 80,56%, e isso ainda precisa acontecer quatro vezes.

Em seguida, os cabeças de chave número 4 enfrentarão os cabeças de chave número 5. Isso já aconteceu 73 vezes, e em 41 delas o cabeça de chave número 4 venceu, o que representa uma probabilidade de 56,16% em cada partida. E ainda temos quatro divisões, então vamos elevar isso à quarta potência.

Então, os cabeças de chave número 3 jogarão contra os cabeças de chave número 6. Os cabeças de chave número 3 venceram 41 das 70 partidas, o que representa uma probabilidade de vitória de 58,57% em cada jogo. Finalmente, para passar para a segunda rodada, os cabeças de chave número 2 jogarão contra os cabeças de chave número 7. Os cabeças de chave número 2 venceram 56 vezes, e isso aconteceu 79 vezes, com uma probabilidade de 70,89% em cada uma delas. Muito bem, então, supondo que você vença todas essas partidas, você avança para a terceira rodada, onde os cabeças de chave número 1 jogarão contra os cabeças de chave número 4.

Isso já aconteceu 61 vezes na história do torneio , e em 44 delas o cabeça de chave número 1 venceu, o que representa uma probabilidade de 72,13% em cada caso. Em seguida, os cabeças de chave número 2 enfrentarão os cabeças de chave número 3. Isso já aconteceu 52 vezes, e em 32 delas o cabeça de chave número 2 venceu. Novamente, isso ainda precisa acontecer quatro vezes.

Supondo que você ganhe todos esses jogos:

Então, restarão apenas os cabeças de chave número 1 e número 2. A probabilidade de um cabeça de chave número 1 vencer um cabeça de chave número 2 é de 35 em 64, novamente, com base em jogos históricos, e isso ainda precisa acontecer quatro vezes nas quatro divisões.

Agora, se você chegar até aqui... terá vencido todas as quatro divisões e terá o time número um no topo em todas elas. É aqui que você começa a escolher aleatoriamente. Você precisa de mais três jogos para determinar o melhor entre os quatro times e, como eu disse na introdução, você escolhe aleatoriamente, então suas chances de vencer em cada partida serão de 1 em 2, e ainda faltam três jogos.

Essa é a sua probabilidade de ganhar usando a minha estratégia , o que equivale a uma probabilidade de 1 em 42.743.890.552. Pronto. Acredito que este seja o cálculo mais preciso disponível para preencher um palpite perfeito do torneio March Madness.

Como mencionei na introdução, você pode melhorar isso analisando as probabilidades atuais no mercado de apostas, e obrigado por assistir a este vídeo. Sei que não foi dos melhores.

Considerem isso uma experiência de aprendizado para mim e, novamente, tudo isso está documentado no meu site wizardofodds.com , na seção de apostas esportivas. Procurem também a página sobre como preencher um chaveamento perfeito para o March Madness. Acho que não há mais nada a acrescentar.

Muito obrigado por assistir.

Escrito por: Michael Shackleford