Sic Bo - Calcule as probabilidades e ganhe | Vídeo

Olá pessoal, aqui é o Mike.

Você vai aprender como calcular as probabilidades no jogo Sic Bo . Resumidamente, o Sic Bo é um jogo chinês muito antigo baseado no lançamento de três dados. Há uma grande variedade de apostas para escolher no jogo.

O que vou fazer :

Dividi este tópico em dois vídeos porque todos no meu fórum estão reclamando que meus vídeos são muito longos. Nesta primeira parte , vou explicar como calcular a probabilidade de obter qualquer total de 3 a 18 com três dados, bem como a probabilidade de obter 0, 1, 2 ou 3 em qualquer face de um dado.

Assim que tivermos as respostas para essas perguntas…

…podemos prosseguir para a segunda parte e analisar que tipo de valor você obtém com as diferentes apostas disponíveis no Sic Bo.

Vamos responder à pergunta : "Qual é a probabilidade de se obter qualquer total dado com três dados de seis lados?" Esta técnica que vou mostrar funciona para qualquer número de dados.

Gostaria de dar os créditos a Robert Goodhand, de Somerset, Reino Unido, por esta pequena e engenhosa técnica. Ela está explicada na minha coluna "Pergunte ao Mago" número 264. Vou compartilhá-la com vocês agora.

Primeiro, precisamos definir cinco quadrados fictícios. Você entenderá o porquê em um minuto. Agora, vou listar todos os totais de 1 a 18. Com um dado, obviamente só há uma maneira de tirar 1, 2 ou 6.

Cada face tem um lado, então é bem óbvio. Com dois dados, o que você quer fazer é somar a coluna à esquerda, neste caso, a coluna B, começando com uma célula, subindo da esquerda para a direita e depois somando as cinco células acima dessa.

No caso em questão…

…Estou trabalhando com a célula C8. Ela representa o número de maneiras de se obter um total de dois com dois dados. Estou somando os valores das células B2 a B7. Se a célula estiver em branco, o Excel assume corretamente que o valor é zero.

Eu simplesmente copio e colo isso para todos os totais possíveis até 12. Você verá que para um total de dois, há uma maneira de jogar. Para um total de três, há duas maneiras. Para um total de quatro, há três maneiras.

Bem, por que isso funciona?

Vamos considerar apenas o total de dois. Para obter um total de dois, o primeiro dado precisa ser um e o segundo dado também precisa ser um. Há apenas uma maneira de o primeiro dado ser um e, obviamente, apenas uma maneira de o segundo dado ser um. Para um total de três, há duas maneiras.

Há uma maneira de o primeiro dado ser um e o segundo dado ser dois , mais a maneira de o primeiro dado ser dois e o segundo dado ser um. Para um total de quatro, o primeiro dado tem que ser de um a três.

Num total de cinco...

O primeiro dado deve ter um total de um a quatro. Contanto que o primeiro dado esteja dentro desse intervalo aceitável, há uma maneira de o próximo dado atingir o total desejado.

Vamos prosseguir com três dados.

É exatamente a mesma técnica. Podemos simplesmente copiar e colar a mesma fórmula. Eu poderia pegar isso de qualquer lugar no intervalo que acabamos de fazer. Vou fazer isso aqui, copiar e colar uma célula para a direita e copiar e colar para baixo. Aí temos o número de combinações para qualquer total de 3 a 18 com três dados.

Por exemplo:

Há uma maneira de rolar um total de três, três maneiras de rolar um total de quatro, seis maneiras de rolar um total de cinco e assim por diante. Por que isso funciona? Você pode perguntar novamente. Bem, vamos analisar um total de sete, por exemplo. Para obter um total de sete com três dados, isso pode ser feito se o total com dois dados for dois e, em seguida, você adicionar um cinco a ele.

Há uma maneira de os dois primeiros dados somarem dois. Outra maneira é se a soma dos dois primeiros dados for três e o terceiro dado for quatro. Como acabamos de ver, há duas maneiras de a soma dos dois primeiros dados ser três e três maneiras de a soma dos dois primeiros dados ser quatro.

Para obter um total de sete …

…os seus dois primeiros dados devem somar um total de dois a seis. Acabamos de ver que o número total de possibilidades é a soma dos números de um a cinco, que é 15. Vamos organizar tudo isso em uma tabela prática. Aqui está o total novamente.

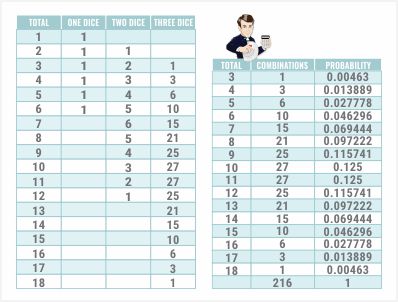
Eis as combinações :

Vamos somar tudo isso, 216. Esse número parece familiar. Talvez seja seis elevado ao cubo.

Finalmente, vamos calcular a probabilidade de cada total:

Basta dividir o número de combinações pelo total. Essa é a probabilidade de rolar qualquer total entre 30 e 18. Em seguida, vejamos a probabilidade de rolar qualquer face específica do dado de zero a três vezes. Existem seis apostas diferentes no Sic Bo, uma para cada face do dado.

O jogador ganha uma para uma se a face escolhida sair uma vez, duas para uma se sair duas vezes e três para uma se sair três vezes. Agora, muitas pessoas somam as probabilidades incorretamente quando estão falando de múltiplos eventos e cada dado é como um evento independente.

Não somamos, multiplicamos.

Adoro pensar primeiro nas coisas em termos de combinações. Digamos que você escolha o seis, por exemplo. Qual é... ou melhor, qual é o número de combinações possíveis para que o seis apareça três vezes em três dados? Bem, é simplesmente uma. Só existe uma maneira de isso acontecer: 6-6-6. E se aparecer duas vezes?

Por exemplo:

6-6-4 ou 2-6-6, 6-1-6. Dois dos dados são um seis e um deles é outro número. Esse outro número pode ser qualquer uma das outras cinco faces, e esse outro número pode aparecer em qualquer um dos três dados. O número total de maneiras que a face escolhida pode aparecer duas vezes em três dados é 15.

E quanto ao número de maneiras pelas quais ele pode aparecer uma única vez?

Bem, os outros dois dados que não são a face escolhida podem ser qualquer uma de cinco coisas. Multiplicamos 5 x 5 porque um deles pode ser qualquer coisa diferente de um seis ou qualquer outra face que você tenha escolhido, e o outro também pode ser qualquer uma das outras cinco faces.

Finalmente…

…multiplicamos por três porque o dado que representou a face escolhida pode ser qualquer um dos três dados. O número de maneiras de rolar a face escolhida uma vez é 5 x 5 x 3, que é igual a 75. Por exemplo, digamos que você escolheu a face seis; poderia ser 6-1-2, 1-4-6, 1-6-5, 2-6-2, 6-1-3 e assim por diante.

E quanto ao número de combinações em que você não tira nenhum dos valores do dado que corresponde à sua escolha?

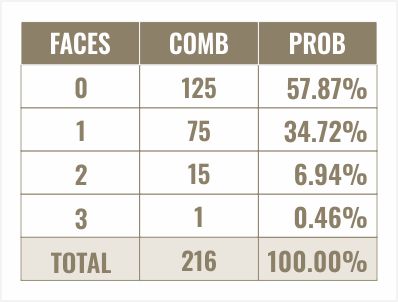
Bem, cada um dos três dados pode ser uma de cinco coisas. Cinco dados — quer dizer, três dados — cinco combinações diferentes para cada um, além da face escolhida, são 5 x 5 x 5 combinações, ou 125. Vamos somar todas essas combinações e obtemos 216 novamente. Novamente, isso é seis elevado à terceira potência, então devo ter feito algo certo.

Finalmente, vamos analisar a probabilidade.

Simplesmente dividimos o número de combinações pelo total de combinações. Vamos colocar isso em porcentagem. Aqui vemos que a probabilidade de rolar a face escolhida zero vezes é de 57,87%, uma vez, 34,72%, duas vezes, 6,94% e três vezes, 0,46%.

Espero que tenha ficado claro. Espero ver vocês na segunda parte, onde calcularei as probabilidades de várias apostas diferentes no Sic Bo.

Obrigado por assistir.

Este documento foi criado com as ferramentas do editor HTML instantâneo. Clique aqui e experimente gratuitamente.

Parte 2

Escrito por: Michael Shackleford