Pergunte ao Mago #164
Em sua coluna de 5 de abril de 2006, você afirma que, se restarem apenas duas maletas no programa "Deal or No Deal" e o prêmio de um milhão de dólares ainda estiver em jogo, a probabilidade de a minha maleta ganhar o milhão é de 50%. Discordo. Isso não seria apenas uma variação do problema de Monty Hall? Ou seja, o milhão tem mais probabilidade de estar no palco do que na maleta dele?
Não. Muita gente está discutindo comigo sobre isso. Muitos autores afirmam que as probabilidades não mudam se novas informações forem introduzidas. Então, se a probabilidade começa em 1 em 26, ela deve permanecer assim. Ao contrário do que dizem os vendedores de sistemas de apostas, as probabilidades podem, sim, mudar conforme novas informações são introduzidas. Não quero tentar ensinar probabilidade básica aqui, mas qualquer livro de matemática de nível universitário sobre probabilidade condicional ou o Teorema de Bayes deve abordar esse tópico muito bem.
Deixe-me explicar o que acontecia no programa "Let's Make a Deal". O participante escolhia uma entre três cortinas. Uma continha um prêmio muito valioso e as outras duas, prêmios menores. Para fins de argumentação, digamos que atrás de uma cortina havia um carro e atrás das outras duas, uma cabra. Então, Monty sempre, repito, SEMPRE, abria uma das duas cortinas não escolhidas para revelar uma cabra. Depois de centenas de programas, isso implicaria que Monty Hall (o apresentador) sabia onde estava o carro e abria deliberadamente uma cortina que revelava uma cabra. Obviamente, quando o jogador escolhia sua cortina, a probabilidade de ela conter o carro era de 1/3 e a probabilidade de uma das duas cortinas não escolhidas conter o carro era de 2/3. Monty, então, estava predestinado a abrir uma cortina não escolhida que continha um prêmio. Predestinado é a palavra-chave aqui. Como Monty não podia abrir a cortina do jogador nessa etapa, a probabilidade de a cortina do jogador revelar o carro permanecia em 1/3. A probabilidade de uma cortina não escolhida revelar o carro permanece em 2/3, porém agora está toda concentrada em uma única cortina. Portanto, após a revelação de um bode, a probabilidade de a cortina do jogador conter o carro é de 1/3 e a probabilidade de a outra cortina fechada conter o carro é de 2/3, tornando a troca uma escolha sábia.
A tabela a seguir mostra todos os resultados possíveis. No caso em que o jogador escolheu a cortina com o carro, eu fiz com que Monty abrisse uma cortina aleatoriamente. Você pode ver que não trocar resulta em uma probabilidade de 1/3 de ganhar, e trocar resulta em uma probabilidade de 2/3 de ganhar.
Vamos fazer um acordo
| Jogador Escolhe | Carro | Cortina Aberto | Probabilidade | Ganhe por Comutação |
| 1 | 1 | 1 | 0% | n / D |
| 1 | 1 | 2 | 5,56% | N |
| 1 | 1 | 3 | 5,56% | N |
| 1 | 2 | 1 | 0% | n / D |
| 1 | 2 | 2 | 0% | n / D |
| 1 | 2 | 3 | 11,11% | Y |
| 1 | 3 | 1 | 0% | n / D |
| 1 | 3 | 2 | 11,11% | Y |
| 1 | 3 | 3 | 0% | n / D |
| 2 | 1 | 1 | 0% | n / D |
| 2 | 1 | 2 | 0% | n / D |
| 2 | 1 | 3 | 11,11% | Y |
| 2 | 2 | 1 | 5,56% | N |
| 2 | 2 | 2 | 0% | n / D |
| 2 | 2 | 3 | 5,56% | N |
| 2 | 3 | 1 | 11,11% | Y |
| 2 | 3 | 2 | 0% | n / D |
| 2 | 3 | 3 | 0% | n / D |
| 3 | 1 | 1 | 0% | n / D |
| 3 | 1 | 2 | 11,11% | Y |
| 3 | 1 | 3 | 0% | n / D |
| 3 | 2 | 1 | 11,11% | Y |
| 3 | 2 | 2 | 0% | n / D |
| 3 | 2 | 3 | 0% | n / D |
| 3 | 3 | 1 | 5,56% | N |
| 3 | 3 | 2 | 5,56% | N |
| 3 | 3 | 3 | 0% | n / D |
Enquanto isso, em "Deal or No Deal", nada é predeterminado. Vamos supor que, em "Deal or No Deal", os valores restantes sejam de US$ 0,01, US$ 1 e US$ 1.000.000. Com três maletas restantes, É possível que a maleta aberta contenha o prêmio de um milhão de dólares. A tabela a seguir mostra os possíveis resultados com três maletas restantes. Lembre-se: o jogador não pode abrir sua própria maleta.
Acordo ou não acordo
| Jogador Escolhe | Milhões de dólares | Caso Aberto | Probabilidade | Ganhe por Comutação |
| 1 | 1 | 1 | 0% | n / D |
| 1 | 1 | 2 | 5,56% | N |
| 1 | 1 | 3 | 5,56% | N |
| 1 | 2 | 1 | 0% | n / D |
| 1 | 2 | 2 | 5,56% | Sem esperança |
| 1 | 2 | 3 | 5,56% | Y |
| 1 | 3 | 1 | 0% | n / D |
| 1 | 3 | 2 | 5,56% | Y |
| 1 | 3 | 3 | 5,56% | Sem esperança |
| 2 | 1 | 1 | 5,56% | Sem esperança |
| 2 | 1 | 2 | 0% | n / D |
| 2 | 1 | 3 | 5,56% | Y |
| 2 | 2 | 1 | 5,56% | N |
| 2 | 2 | 2 | 0% | n / D |
| 2 | 2 | 3 | 5,56% | N |
| 2 | 3 | 1 | 5,56% | Y |
| 2 | 3 | 2 | 0% | n / D |
| 2 | 3 | 3 | 5,56% | Sem esperança |
| 3 | 1 | 1 | 5,56% | Sem esperança |
| 3 | 1 | 2 | 5,56% | Y |
| 3 | 1 | 3 | 0% | n / D |
| 3 | 2 | 1 | 5,56% | Y |
| 3 | 2 | 2 | 5,56% | Sem esperança |
| 3 | 2 | 3 | 0% | n / D |
| 3 | 3 | 1 | 5,56% | N |
| 3 | 3 | 2 | 5,56% | N |
| 3 | 3 | 3 | 0% | n / D |
O que a tabela do Deal or No Deal mostra é que, com três caixas restantes, a probabilidade de o jogador abrir a caixa de um milhão de dólares é de 1/3 (sem chance de ganhar), a probabilidade de um jogador que troca de caixa ganhar é de 1/3 e a probabilidade de um jogador que troca de caixa perder é de 1/3. Portanto, as chances de trocar de caixa são as mesmas. Quando restam apenas duas caixas, a probabilidade de cada caixa conter o prêmio maior é de 50/50.
Adoro o site!! Como mencionei em resposta a outra pergunta, alguns cassinos oferecem a Mão do Dragão no pôquer pai gow . Minha teoria é jogá-la se eu tiver uma trinca ou melhor, de preferência sem o curinga. Outros jogam quando não têm nada. Existe alguma lógica em alguma dessas metodologias?
Eu nunca jogo a mão do dragão porque ela sempre perde em mãos repetidas. Independentemente das suas cartas, você tem as mesmas chances de formar qualquer mão que o dealer, assumindo a mesma estratégia. Então, se você insistir em jogá-la, pode fazê-lo quando quiser.
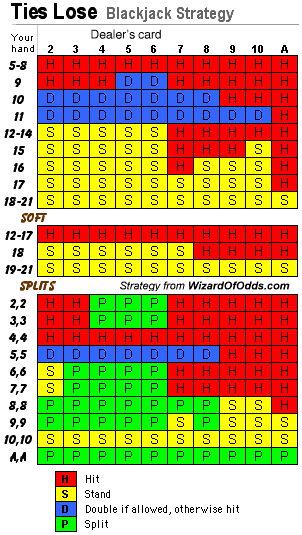
Eu sou crupiê de blackjack na festa da minha igreja e adoraria apresentar um cenário básico de estratégia para as nossas regras...
4 baralhos
O revendedor está em cima do 17 macio
Duplo em 9, 10, 11
Divida quaisquer cartas
Dobro após divisão
JOGADOR PERDE EMPURRÕES
A última regra é o que eu chamo de "Vantagem da Casa de Deus" e é a única regra que obviamente não está em nenhum dos geradores de estratégia que encontrei online. Estou convencido de que a regra de empate perde pode tornar tirar 17 uma jogada básica de estratégia em alguns casos. Atenciosamente e continuem com o ótimo trabalho.
Não existe um mandamento na Bíblia sobre roubar? Mostro que a vantagem da casa nesse jogo é de 9,3% (ai!). Aqui está a estratégia básica apropriada para esta variação de Blackjack em que o empate perde. Veja a coluna nº 110 para a versão em que o jogador pode dobrar a aposta com mãos fracas.
Eu estava jogando bacará online no USACasino, que usa um dealer ao vivo e o software da Playtech. Aparentemente, a Playtech implementou uma nova regra segundo a qual o dealer descarta uma carta após cada mão ser distribuída. Não é assim que se joga nos cassinos. Que impacto, se é que há algum, isso tem nas probabilidades do jogo? Não consigo acreditar que o cassino implementaria uma nova regra que não fosse a seu favor.
Queimar cartas não afeta o jogador que usa a estratégia básica. Provavelmente, fazem isso para desencorajar quem conta cartas. No entanto, poderiam simplesmente embaralhar mais cedo. Para fins de contagem de cartas, o importante é o número de cartas visíveis; não importa se as cartas não vistas são queimadas ou estão atrás da carta de corte.
Recentemente visitei o Imperial Palace, em Las Vegas, e joguei craps. Fiquei muito surpreso ao descobrir que as apostas Horn pagam 15 para 1 e 30 para 1 (14 para 1 e 29 para 1, respectivamente). Quão drasticamente isso altera a vantagem da casa? E você conhece algum outro cassino que não pague o padrão de 15 para 1 e 30 para 1?
Como se as probabilidades normais já não fossem ruins o suficiente. Que vergonha para o IP. Diminuir as apostas de chifre de 2 números de 15 para 14 aumenta a vantagem da casa de 11,11% para 16,67%. Diminuir as apostas de chifre de 1 número de 30 para 29 aumenta a vantagem da casa de 13,89% para 16,67%. Não, eu não conheço nenhum outro cassino que faça isso, mas também não procuro por esse tipo de coisa.
Olá Wiz, como sempre, obrigado pelo ótimo site e adoro suas colunas, especialmente as perguntas sobre relacionamentos. Tenho uma dúvida sobre meu jogo de blackjack online. Jogo há bastante tempo e mantenho um registro dos meus resultados. Jogo duas mãos de $5 contra o dealer, totalizando uma aposta inicial de $10. Meu valor total apostado, incluindo dobradas e divisões, está um pouco acima de $680.000 neste momento. Calculei que minha perda esperada seria de $3.000 (após considerar o número total de apostas nas apostas iniciais/mãos) com uma vantagem da casa de 0,5%. No entanto, minha perda real foi muito maior, de $8.500. Para uma amostra de tamanho razoável, essa parece ser uma discrepância bastante grande. Não sei se isso significa que o jogo é injusto (não tenho motivos para acreditar nisso) ou se estou apenas tendo azar. O que você acha? Há algum motivo para suspeitar com base nesses resultados? PS: Felizmente, ainda estou ganhando dinheiro graças aos bônus, mas não tanto quanto eu esperava, e essa é a parte decepcionante. Obrigado e tudo de bom.
Obrigado pelas gentis palavras. Então, você jogou 680.000/5 = 136.000 mãos. De acordo com o meu apêndice 4 sobre blackjack, o desvio padrão por mão, jogando duas mãos simultaneamente, é de 1,91. Portanto, o desvio padrão de 136.000 mãos seria de 136.000 * 0,5 * 1,91 = 704 mãos. Suas perdas acima do esperado são de US$ 5.500, ou 1.100 mãos. Assim, você está 1.100/704 = 1,56 desvios padrão abaixo do esperado. A probabilidade de ter um desempenho tão ruim ou pior pode ser encontrada no Excel como normsdist(-1,56) = 5,94%.
Eu tinha um blackjack e o crupiê me pagou. No final da rodada, ele virou as cartas e descobriu que também tinha um blackjack. Ele se esqueceu de conferir a mão antes de me pagar. Os supervisores queriam que eu devolvesse os ganhos. Eu me recusei. Parece que me lembro de um cenário semelhante de um livro sobre blackjack. Eu estava certo?
Eu digo que você deveria ter devolvido os ganhos. Nunca vi isso abordado em nenhum livro. No entanto, será que um livro é realmente necessário? É para isso que você tem a consciência. Pediram que você corrigisse as coisas, e é a coisa certa a fazer.
Fiz uma aposta all-in após o flop. O único jogador restante na mão pensou por alguns segundos e me mostrou as cartas dele. As cartas nunca tocaram a mesa, ele não disse uma palavra, mas interpretei isso como um sinal de desistência. Então, descartei minhas cartas e peguei as fichas, e ele afirmou que ainda não havia desistido. Agora que ele viu minhas duas cartas, decidiu pagar e ganhou com a carta do river. Isso é legal ou não?
O pôquer é um dos meus jogos mais fracos quando se trata de apostas, então recorro novamente ao JB para esta. Aqui está o que ele disse.
Essa jogada é completamente ilegal. Sempre que alguém mostra suas cartas para um oponente, a mão é encerrada. A única exceção é quando ambos os jogadores declaram "all-in". Nesse momento, ambas as mãos são mostradas e a mão é concluída. Nesse caso, o jogador que mostrou as cartas para o oponente perde a mão e o outro jogador vence.Depois de receber essa resposta, lembrei-me de uma cena de um filme, acho que era Stuey , em que um jogador se oferece para virar uma de suas cartas, escolhida pelo outro jogador, por 100 dólares. Perguntei ao JB se a cena era realista. Aqui está a resposta dele para essa pergunta.
Isso sempre acontecia em torneios e era perfeitamente aceitável naquela época. Foi por volta de 2001 ou 2002 que essa regra foi formalmente alterada em quase todas as salas de poker. Eu estava em um torneio na semana passada e estava com poucas fichas. Dei all-in com AQ suited. Todos desistiram até o big blind, que tinha muitas fichas. Depois de pensar por uns dois minutos, ele me mostrou o KQ que tinha e voltou a pensar se deveria pagar. Chamei o supervisor e disse que ele havia me mostrado as cartas antes de tomar uma decisão e que a mão deveria ser considerada morta. Ele concordou comigo, a mão foi automaticamente declarada morta e ele recebeu uma penalidade de cinco minutos, durante a qual teve que sair da mesa, o que lhe custou cerca de cinco mãos. Os blinds e antes eram altos, então a penalidade lhe custou vários milhares de fichas de torneio.


