Pergunte ao Mago #171
Eu não entendo seu jogo NIM ! Sempre achei que a chave para ganhar é deixar o oponente (nesse caso, o computador) com pontos cuja soma seja igual ao menor número binário correspondente, ou seja, se eu tiver 17 pontos, retiro 2 e deixo 15, que é a soma dos números binários 1, 2, 4 e 8. Mas isso não parece funcionar. Estou certo ou errado?
Você está no caminho certo com os números binários, mas essa não é exatamente a estratégia vencedora. Primeiro, se você puder deixar seu oponente com um número ímpar de linhas com apenas um elemento cada, faça isso. Caso contrário, decomponha cada linha em seus componentes binários. Por exemplo, 99 seria 64 + 32 + 2 + 1. Em seguida, some o número de cada componente em todas as linhas. Depois, procure uma jogada que deixe seu oponente com um número par de todos os componentes binários em todas as linhas.
Vejamos um exemplo. Suponha que seja a sua vez, com o seguinte cenário.
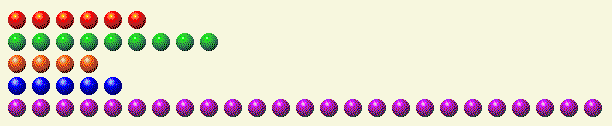
A tabela a seguir detalha cada linha em seus componentes binários.
Turno do Jogador 1
| Linha | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 25 | 1 | 0 | 0 | 1 | 1 |
| Total | 3 | 1 | 3 | 2 | 1 |
Você pode ver que há um número ímpar de uns, dois, quatros e dezesseis. Claramente, precisamos reduzir a linha de 25 para menos de 16 para eliminar a unidade 16. Para manter o total dos componentes binários par, precisamos remover o 1, adicionar um 2, adicionar um 4, manter o 8 e remover o 16. Isso significa que a melhor jogada é 2+4+8=14 na última linha. Deixando 14 na última linha, temos o seguinte.
Turno do computador 1
| Linha | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| Total | 2 | 2 | 4 | 2 | 0 |
O computador faz a sua parte, deixando-nos com isto.
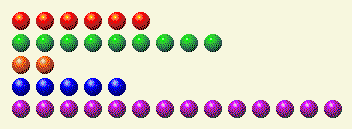
Aqui está a análise binária disso.
Turno do Jogador 2
| Linha | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| Total | 2 | 3 | 3 | 2 | 0 |
Aqui precisamos remover um 2 e um 4 para que os totais fiquem iguais. Há apenas uma linha, a 14, que contém ambos os componentes. Portanto, remova 6 dessa linha, restando 8.
Turno do Computador 2
| Linha | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| Total | 2 | 2 | 2 | 2 | 0 |
O computador faz a sua parte, deixando-nos com isto.
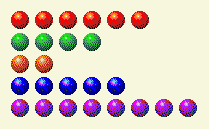
Agora precisamos alterar as colunas 1, 4 e 8.
Turno do Jogador 3
| Linha | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| Total | 1 | 2 | 3 | 1 | 0 |
Isso pode ser feito alterando a linha de 8 para 5, da seguinte forma.
Turno do Computador 3
| Linha | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| Total | 2 | 2 | 4 | 0 | 0 |
O computador faz a sua parte, deixando-nos com isto.
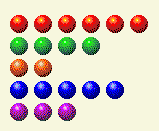
Agora precisamos alterar os totais de 2 e 4.
Turno do Jogador 4
| Linha | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Total | 2 | 3 | 3 | 0 | 0 |
Isso pode ser feito alterando o 6 para 0.
Turno 4 do computador
| Linha | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Total | 2 | 2 | 2 | 0 | 0 |
O computador faz a sua parte, deixando-nos com isto.
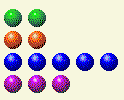
Agora precisamos trocar os números 2 e 4.
Turno do Jogador 5
| Linha | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Total | 2 | 3 | 1 | 0 | 0 |
Isso pode ser conseguido alterando a linha de 5 para 3. Se você conseguir levar seu oponente a uma situação x,x,y,y, você certamente vencerá, desde que consiga manter essa situação até o final.
Turno do Computador 5
| Linha | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Total | 2 | 4 | 0 | 0 | 0 |
Nas próximas jogadas, mantenho o computador nos padrões x,x,y,y. Aqui, o computador me deixa com 2,2,3,2; então, eu o deixo com 2,2,2,2.

O computador então me dá 2,2,1,2. Eu o deixo com 2,2,1,1.
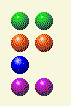
O computador então me deixa com 2, 2, 1. Eu o deixo com 2, 2. Se você conseguir fazer com que seu oponente fique com duas fileiras iguais, você certamente ganhará; basta manter as fileiras iguais.

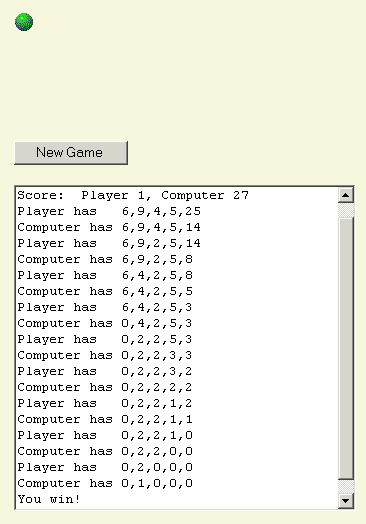
O computador então me deixa com uma única pilha de 2, e eu removo 1.

Aqui termina o jogo.
Entendo que a aposta put é vantajosa quando as odds são de 10x ou mais. Por exemplo, se o ponto for 6 ou 8, aposte $5 mais $50 de odds grátis. Minha dúvida é: por que esperar pelo ponto? Por que não apostar na linha de passe e, se o ponto for 6 ou 8, apostar as odds completas de 10x? Dessa forma, você aproveita a vantagem das odds, além da vantagem de um lançamento de 7/11. Estou perdendo alguma coisa?
Concordo. Não recomendo fazer apostas "put" ou "place", porque, como você disse, as probabilidades são melhores fazendo uma aposta na linha e depois apostando no máximo. No entanto, algumas pessoas absolutamente precisam apostar nos pontos diretamente. Se esse for o caso, defendo fazer a melhor aposta entre "place", "buy" e "put", o que explico com mais detalhes na minha seção de craps.
Eu e meu amigo estávamos jogando em Las Vegas. Tivemos uma grande discussão sobre qual das duas opções tinha probabilidades estatisticamente melhores: dobrar a aposta com o jogador totalizando 10 contra o dealer mostrando 7, ou dobrar a aposta com o jogador totalizando 11 contra o dealer mostrando 10, em um jogo com dois baralhos. Eu achava que era a primeira opção.
Meu apêndice 9 sobre blackjack foi criado justamente para esse tipo de pergunta. Considerando 6 baralhos, minha tabela mostra que o valor esperado de dobrar 8+2 contra 7 é 0,396342. O valor esperado de dobrar 8+3 contra 10 é 0,176919. Portanto, você está certo, 10 contra 7 é uma mão muito melhor.
Seu site é incrível, aprendi muito com ele. No flop do pôquer Hold'em, se você tem 20 cartas que formam a mão vencedora, por que a porcentagem de você completar a mão até o river é de 67,5% e não de 86% (20/47 + 20/46)? Procurei em todos os lugares e não consigo entender, mesmo sabendo que provavelmente é algo muito básico. Agradeceria muito a ajuda, obrigado!
Obrigado! Seu método conta duas vezes, pois você consegue duas das 20 cartas necessárias. A probabilidade de conseguir uma das 20 cartas necessárias no turn é 20/47 = 0,4255. A probabilidade de não conseguir no turn e conseguir no river é (27/47)*(20/46) = 0,2498. Portanto, a probabilidade total é 0,4255 + 0,2498 = 0,6753.
Recentemente, presenciei uma situação intrigante no cassino tribal local, relacionada ao protocolo da mesa de dados, e gostaria de saber se você poderia me esclarecer. Na sua primeira jogada, o Jogador 'A' tirou um número e estabeleceu um ponto. Na jogada seguinte, o jogador ao lado de 'A' (Jogador 'B') pegou os dados e jogou. Não ficou claro por que ele fez isso, ou mesmo se ele conhecia 'A'. Um dos outros jogadores protestou, apontando que 'B' não era o jogador que havia lançado os dados inicialmente. Após muita discussão e perplexidade por parte dos crupiês e do responsável pela mesa, os dados foram passados para o próximo jogador (Jogador 'C'), que finalizou a mão (ele acabou tirando um sete).
Este era o protocolo correto para esta situação e, em caso afirmativo, qual a lógica por trás dele? Se o Jogador 'A', por algum motivo, simplesmente não quisesse mais jogar, por que ele não deveria ter permissão para devolver os dados? Se o Jogador 'B' pegou os dados porque não entendeu o jogo, ou se o crupiê os colocou na frente dele por engano, os dados não deveriam voltar para 'A' para terminar a rodada?
Perguntei isso ao Bone Man do nextshooter.com . Aqui está o que ele disse.
Se um jogador que não seja o lançador correto pegar os dados e lançá-los, a jogada deve ser anulada e os dados devem ser devolvidos ao lançador correto. Embora esta seja de fato a regra correta, o árbitro, em alguns casos, pode permitir o lançamento se o resultado for favorável a todos ou à maioria dos jogadores. Em alguns casos, o resultado do lançamento pode não afetar as apostas de nenhum jogador. Além disso... Qualquer jogador pode solicitar que os dados sejam enviados ao próximo lançador para finalizar uma rodada. Nesses casos, os mesmos dados podem ser enviados ou o novo lançador pode solicitar novos dados. Após a conclusão do lançamento, o MESMO lançador pode então lançar SUA PRÓPRIA MÃO, tendo assim mais de uma mão.
Qual a probabilidade de obter uma soma superior a 100 ao lançar 20 dados? Atenciosamente,
Comecei a usar a aproximação Normal para resolver isso, mas a probabilidade de obter mais de 100 pontos é muito baixa para que esse método seja preciso. Então, fiz uma simulação aleatória com 8,25 milhões de tentativas e o número de tentativas com 101 pontos ou mais foi 127. Portanto, a probabilidade é de aproximadamente 1 em 65.000.
Hora de mais uma pergunta do "Deal or No Deal". Digamos que, depois de todas as ofertas do banqueiro e das participações especiais da Celine Dion, você fique com duas maletas: uma com US$ 500.000 e outra com US$ 1.000.000. A oferta do banqueiro será um pouco menor que US$ 750.000, eu imagino. Qual você escolheria? E se as duas maletas restantes fossem a de US$ 0,01 e a de US$ 1.000.000? Acho que tudo depende se você gosta de apostar ou não, e não tem nada a ver com probabilidades. O motivo da minha pergunta é que me pergunto se ALGUÉM algum dia ganhará US$ 1.000.000 (mesmo que tenha escolhido a maleta mágica).
Quando os prêmios se tornam quantias que mudam a vida, o jogador sábio deve jogar de forma conservadora, mesmo que isso signifique sacrificar a maximização do valor esperado. Uma boa estratégia seria maximizar a felicidade esperada. Uma boa função para medir a felicidade, na minha opinião, é o logaritmo da riqueza total. Vamos considerar uma pessoa com um patrimônio de US$ 100.000 que recebe duas ofertas: uma de US$ 0,01 e outra de US$ 1.000.000. Ao optar por "não aceitar", a felicidade esperada é de 0,5 * log(US$ 100.000,01) + 0,5 * log(US$ 1.100.000) = 5,520696. Seja b a oferta do banco, na qual o jogador é indiferente.
log(b) = 5,520696
b = 10 5,520696
b = $331.662,50.
Portanto, esse jogador hipotético deveria ser indiferente a uma oferta do banco de US$ 331.662,50. Quanto menor for sua riqueza antes do jogo, mais conservador você deve jogar. Normalmente, nas fases finais do jogo, as ofertas do banco se aproximam do valor esperado, às vezes um pouco acima. O único caso racional em que um jogador poderia ganhar o milhão é se ele tivesse muita riqueza antes do jogo e/ou as ofertas do banco fossem excepcionalmente baixas. Os produtores parecem gostar de pessoas trabalhadoras da classe média, então é improvável que vejamos alguém que possa se dar ao luxo de ser imprudente quando grandes quantias estão envolvidas. Eu também nunca vi o banco fazer ofertas abaixo de 90% do valor esperado nas fases finais do jogo. O momento em que veremos alguém ganhar o milhão será quando um jogador compulsivo entrar no programa e não conseguir parar. Quando isso acontecer, estarei torcendo pelo banqueiro.
Adoro seu site! Acabei de encontrar sua lista detalhada das mesas de Blackjack de Las Vegas e suas respectivas vantagens, então fiquei com uma dúvida: suponha que existam duas mesas de Blackjack, uma com vantagem de 0,2% e aposta mínima de $10, e outra com vantagem de 0,4% e aposta mínima de $5. Ambas as mesas têm a mesma perda de $0,02 por mão. Existe alguma vantagem em escolher uma mesa em vez da outra?
Obrigado. Para responder a essa pergunta, você primeiro precisa se perguntar por que está jogando. Se você está tentando perder o mínimo possível, então não deveria jogar. No entanto, se você está jogando por diversão, eu escolheria o jogo de $10 com a vantagem de 0,2%. A perda esperada será a mesma, mas você terá uma experiência mais emocionante com apostas maiores.
Existe uma aposta paralela de Pai Gow Poker no Casino Niagara que paga com um jackpot em vez de odds fixas. Gostaria de saber qual o valor mínimo que o jackpot deve atingir para que essa aposta seja vantajosa (considerando que a mão seja formada para maximizar o retorno da aposta no jackpot).
O ponto de equilíbrio é de US$ 102.680,24. Acabei de adicionar uma análise dessa aposta à minha seção sobre apostas paralelas no Pai Gow Poker .
Não entendo muito de pôquer, mas acho divertido, então talvez você possa me esclarecer uma dúvida. Em uma viagem recente a Las Vegas com minha esposa, ficamos no Arizona Charlie's Decatur. Escolhemos o hotel porque eles anunciavam mesas de Hold'em de $2 a $4 no site. Na nossa primeira manhã, fomos até a sala de pôquer e nos inscrevemos para jogar $2-$4. Percebi que o funcionário do pôquer estava anotando nossos nomes nas colunas de $4-$8. Então, expliquei que queríamos jogar $2-$4 (havia uma coluna com a inscrição “$2-$4” na mesma folha). Ele disse que era $2-$4: $2 antes do flop, $4 depois do flop e $8 depois do turn e do river. Expliquei o que eu queria dizer com $2-$4: $2 antes e depois do flop e $4 depois do turn e do river. Ele riu de nós como se não soubéssemos do que estávamos falando e disse que não era assim que o jogo funcionava. Acabamos jogando pôquer no Gold Coast pelo resto da viagem. Esse tipo de aposta é normal em salas de pôquer? (Acabei dizendo ao supervisor da sala de pôquer que se pudéssemos bancar uma partida de Hold'em de US$ 4 a US$ 8, não estaríamos hospedados no Arizona Charlie's.)
Concordo que um jogo "2/4" significa que as apostas são de $2 antes do turn e $4 depois do turn. No entanto, o small blind provavelmente é de $1. Parece que quando o Arizona Charlie's chama um jogo de "2/4", eles estão se referindo aos blinds, o que significaria um small blind de $2 e um big blind de $4, o que implicaria apostas de $8 após o turn. Nunca ouvi esse uso antes, então não te culpo por estar surpreso.
P.S.: Mais tarde, recebi a seguinte mensagem de Anthony, um supervisor da sala de pôquer.
Sou supervisor de uma sala de poker. Estou escrevendo para informar sobre a terminologia correta para os limites no Texas Hold'em. Quando um jogo é mencionado como $2/$4, está se referindo às apostas. (Um jogo só é mencionado pelos blinds se for No-Limit.) $2 no pré-flop e pós-flop, $4 no turn e no river. Um jogo listado como $2/$4/$8 (que é exatamente o que suspeito que o autor da carta anterior estava se referindo) significa $2 no pré-flop, $4 no pós-flop, $8 no turn e no river. Também é possível que um jogo seja listado como $2/$4/$6/$8. Estou apenas repassando a informação, pois bons supervisores de poker querem que as pessoas tenham o máximo de informações possível.


