Pergunte ao Mago #253
Não entendo como é possível que nas suas tabelas de poder do Texas Hold'em, o A-7 tenha uma classificação inferior ao KJ suited, mas na sua calculadora o A7 tenha uma probabilidade maior de ganhar.
Boa pergunta. Para benefício de outros leitores, aqui estão as probabilidades contra uma mão aleatória com cada uma dessas duas mãos iniciais em um jogo de dois jogadores:
KJ de terno vs. A-7 sem terno
| Mão | Ganhar | Perder | Empate | Valor Esperado |
K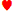 J J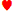 | 0,6148 | 0,3634 | 0,0218 | 0,2513 |
UM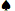 7 7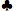 | 0,5717 | 0,3949 | 0,0334 | 0,1768 |
No entanto, de acordo com minha calculadora de Texas Hold'em para dois jogadores, as probabilidades dessas duas mãos se enfrentarem são:
A7 vence = 53,52%
Vitórias de KJ = 46,10%
Empate = 0,39%
Então, o Rei Valete de naipe único está classificado mais alto na minha tabela, mas é inferior ao Ás 7 de naipe único em um confronto direto. Por quê?
A resposta é difícil de explicar. Com duas mãos se enfrentando, é preciso considerar como elas interagem entre si. Por exemplo, na tabela de força inicial das mãos, AK fora do naipe é apenas ligeiramente melhor que AQ fora do naipe, com valores esperados de 0,3064 e 0,2886, respectivamente. No entanto, se as compararmos diretamente, o AK supera o AQ, como segue:
AK vence 71,72%
AQ vence = 23,69%
Empate = 4,58%
No jogo A7 offsuit contra KJ suited, o ás é muito superior ao rei e ao valete. A maior chance de vitória do jogador com KJ ocorre se ele formar um par com o rei ou o valete e nenhum ás aparecer. Demonstro que a probabilidade disso é de apenas 37,73%. Os 46,10% restantes da probabilidade de vitória do KJ vêm de mãos mais fortes.
Embora A7 seja forte contra KJ, é mais frequentemente dominado do que KJ por mãos aleatórias.
Talvez seja uma comparação inadequada, mas é semelhante ao jogo pedra, papel e tesoura . Entre jogadores habilidosos, individualmente, cada lançamento deveria ter aproximadamente a mesma força. No entanto, se um jogador joga papel e o outro tesoura, a força não importa, e a tesoura vencerá.
Nos cassinos Bighorn e Longhorn, em Las Vegas, é permitido dobrar a aposta com três cartas no blackjack. Devo fazer alguma alteração na minha estratégia por conta dessa regra?
Um leitor do meu site Wizard of Vegas diz que as seguintes alterações devem ser feitas, em relação à estratégia padrão de vários baralhos em que o dealer pede carta com um 17 suave:
- Golpe suave 13 contra 5 ou 6
- Acertou 2 cartas suaves 15 contra 4
- Acertou 3,3 contra 2
O motivo para pedir carta nas mãos mais fracas é que você pode conseguir uma dobra suave melhor depois de pedir. O valor de pedir carta nos três é maior sob esta regra, porque conseguir um ás seria uma boa dobra de 3 cartas.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Se uma moeda for lançada 100 vezes, qual é a probabilidade de se obter uma sequência de pelo menos 7 caras consecutivas pelo menos uma vez?
Se existe uma expressão simples e não recursiva para a resposta, eu desconheço. No entanto, existe uma resposta recursiva simples.
f(n) = pr(cara no primeiro lançamento) × f(n-1) +
pr(cara no primeiro lançamento, coroa no segundo lançamento)×f(n-2) +
pr(cara nos dois primeiros lançamentos, coroa no terceiro lançamento)×f(n-3) +
pr(cara nos primeiros 3 lançamentos, coroa no terceiro lançamento)×f(n-4) +
pr(cara nos primeiros 4 lançamentos, coroa no quarto lançamento)×f(n-5) +
pr(caras nos primeiros 5 lançamentos, coroas no quinto lançamento)×f(n-6) +
pr(caras nos primeiros 6 lançamentos, coroas no sexto lançamento)×f(n-7) +
pr(caras nos primeiros 7 lançamentos) =
(1/2)×f(n-1) +
(1/2) 2 ×f(n-2) +
(1/2) 3 ×f(n-3) +
(1/2) 4 ×f(n-4) +
(1/2) 5 ×f(n-5) +
(1/2) 6 ×f(n-6) +
(1/2) 7 ×f(n-7) +
(1/2) 7
Onde:
f(n) = probabilidade de sucesso em n lançamentos.
pr(x) = probabilidade de x acontecer.
Planilhas são perfeitas para problemas como este. Nas capturas de tela da planilha abaixo, inseri uma probabilidade de 0 para as células de B2 a B8, porque não é possível obter 7 caras seguidas em 6 ou menos lançamentos. Para a célula B9, inseri a fórmula:
=(1/2)*B8+(1/2)^2*B7+(1/2)^3*B6+(1/2)^4*B5+(1/2)^5*B4+(1/2)^6*B3+(1/2)^7*B2+(1/2)^7
Em seguida, copiei e colei o valor das células B10 para as células B102, o que corresponde a 100 inversões. Essa probabilidade é de 0,317520. Uma simulação aleatória confirma isso.
 | 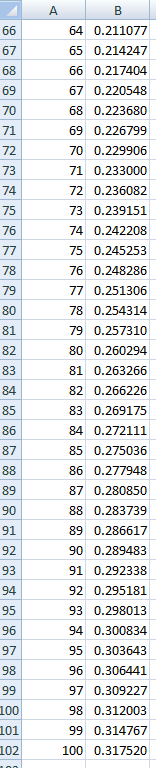 |
Após a publicação original deste texto, Rick Percy compartilhou comigo sua solução em álgebra matricial. Aqui está ela, em minhas próprias palavras. Pressupõe-se que o leitor já conheça os conceitos básicos de álgebra matricial.
Primeiro, existem oito estados possíveis em que o flipper pode estar em qualquer momento:
p 1 = Probabilidade de sucesso, dado que você precisa de mais 7 cabeças a partir do ponto atual.
p 2 = Probabilidade de sucesso, dado que você precisa de mais 6 cabeças a partir do ponto atual.
p 3 = Probabilidade de sucesso, dado que você precisa de mais 5 cabeças a partir do ponto atual.
p 4 = Probabilidade de sucesso, dado que você precisa de mais 4 cabeças a partir do ponto atual.
p 5 = Probabilidade de sucesso, dado que você precisa de mais 3 cabeças a partir do ponto atual.
p 6 = Probabilidade de sucesso, dado que você precisa de mais 2 cabeças a partir do ponto atual.
p 7 = Probabilidade de sucesso, dado que você precisa de mais 1 cara a partir do ponto atual.
p 8 = Probabilidade de sucesso, dado que você não precisa de mais caras = 1.
Vamos definir a matriz S<sub> n</sub> como a probabilidade de estar em cada estado após o n -ésimo lançamento. S <sub>0</sub> representa as probabilidades antes do primeiro lançamento, onde há 100% de chance de estar no estado 0. Portanto, S <sub>0 </sub> =
| 1 0 0 0 0 0 0 0 |
Seja T a matriz de transformação de duas inversões consecutivas, ou seja, de S n para S n+1 , onde S n+1 = T × S n
- Se você estiver no estado 1, após um lançamento de moeda você tem 0,5 de chance de estar no estado 2 (com cara) e 0,5 de permanecer no estado 1 (com coroa).
- Se você estiver no estado 2, após um lançamento de moeda você tem 0,5 de chance de estar no estado 3 (com cara) e 0,5 de chance de retornar ao estado 1 (com coroa).
- Se você estiver no estado 3, após um lançamento de moeda você tem 0,5 de chance de estar no estado 4 (com cara) e 0,5 de chance de retornar ao estado 1 (com coroa).
- Se você estiver no estado 4, após um lançamento de moeda você terá 0,5 de chance de estar no estado 5 (com cara) e 0,5 de chance de retornar ao estado 1 (com coroa).
- Se você estiver no estado 5, após um lançamento de moeda você tem 0,5 de chance de estar no estado 6 (com cara) e 0,5 de chance de retornar ao estado 1 (com coroa).
- Se você estiver no estado 6, após um lançamento de moeda você tem 0,5 de chance de estar no estado 7 (com cara) e 0,5 de chance de retornar ao estado 1 (com coroa).
- Se você estiver no estado 7, após um lançamento de moeda você terá 0,5 de chance de estar no estado 8 (com cara) e 0,5 de chance de retornar ao estado 1 (com coroa).
- Se você estiver no estado 8, significa que obteve sucesso e permanecerá no estado 8 com uma probabilidade de 1,0.
Colocando tudo isso na forma da matriz de transição T =
| 0,5 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,5 0,0 0,0 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,5 0,0 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,5 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,5 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,0 0,5 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,5 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,5 |
| 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 1,0 |
Para chegar à probabilidade de cada estado após um lançamento...
(1) S 1 = S 0 × T
E depois de duas viradas?
(2) S 2 = S 1 × T
Vamos substituir a equação (1) na equação (2)...
(3) S 2 = S 0 × T × T = S 0 × T 2
E depois de 3 flips?
(4) S 3 = S 2 × T
Substituindo a equação (3) em (4)...
(5) S 3 = S 0 × T 2 × T = S 0 × T 3
Podemos continuar fazendo isso até chegar ao estado depois da centésima virada...
S 100 = S 0 × T 100
Então, o que é T 100 ? Antes dos computadores, devia ser uma tarefa extremamente difícil descobrir essas coisas. No entanto, com a função MMULT do Excel e muita cópia e colagem, descobrimos que T 100 =
| 0,342616 0,171999 0,086347 0,043347 0,021761 0,010924 0,005484 0,317520 |
| 0,339863 0,170617 0,085653 0,042999 0,021586 0,010837 0,005440 0,323005 |
| 0,334379 0,167864 0,084271 0,042305 0,021238 0,010662 0,005352 0,333929 |
| 0,323454 0,162380 0,081517 0,040923 0,020544 0,010313 0,005178 0,355690 |
| 0,301693 0,151455 0,076033 0,038170 0,019162 0,009620 0,004829 0,399038 |
| 0,258346 0,129694 0,065109 0.032686 0,016409 0,008237 0,004135 0,485384 |
| 0,171999 0,086347 0,043347 0,021761 0,010924 0,005484 0,002753 0,657384 |
| 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 1,000000 |
O termo no canto superior direito mostra a probabilidade de estar no estado 8 após 100 lançamentos, que é 0,317520.
Recentemente, o cassino Tuscany realizou uma promoção em que, se você conseguisse 30 blackjacks em um período de 30 dias, ganharia um bônus de US$ 100. Inicialmente, a aposta mínima para obter o carimbo no cartão era de US$ 5. No entanto, posteriormente fiquei sabendo que o valor mínimo para o carimbo havia sido aumentado para US$ 15. Escrevi uma carta de reclamação ao gerente do cassino, afirmando, em parte:
Só queria expressar minha decepção com essa mudança, caso seja verdade. Nunca tive a oportunidade de aproveitar a promoção e duvido que consiga agora. O tempo necessário para conseguir 30 blackjacks (disseram-me que são cerca de 8 horas de jogo contínuo) parece irrazoável a US$ 15 por mão, quando a promoção ainda oferece apenas US$ 100.
Eis a resposta que recebi:
Em resposta ao seu e-mail sobre a promoção Blackjack Blackout, não tenho certeza de onde você obteve a informação sobre o tempo necessário para completar o cartão Blackout. Já vimos jogadores completarem o cartão em menos de quatro horas. Além disso, você tem trinta dias para completar o cartão. Espero que entenda que não se trata de uma tarefa impossível com esse tempo disponível. Agradeço sua mensagem. É ótimo receber feedback de nossos clientes. Espero que você possa experimentar e ganhar algum dinheiro!
Qual a probabilidade de se obter 30 blackjacks em quatro horas?
De acordo com minha comparação de jogos , os jogadores de blackjack jogam cerca de 70 mãos por hora. A probabilidade de um blackjack em um jogo com seis baralhos é de 24*96/combin(312,2)=4,75%. Suponho que um empate no blackjack ainda receba um carimbo. Portanto, seriam necessárias cerca de 30/0,0475=632 mãos para completar a cartela, ou 9,02 horas.
A probabilidade de preencher o cartão em 4 horas, considerando 280 mãos, é de 1 em 30.000 jogando uma mão de cada vez. Suspeito que qualquer jogador que tenha alcançado o objetivo em quatro horas estava jogando pelo menos duas mãos simultaneamente.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .


