Pergunte ao Mago #284
Você ouviu falar da concessionária de carros em Seattle que teve que pagar US$ 420.000 porque o Seahawks venceu o Giants sem marcar pontos? Li que eles tiveram que pagar US$ 7.000 pelo seguro contra esse tipo de prejuízo. Qual seria um valor justo de seguro?
De acordo com o artigo " Concessionária de carros de Washington paga US$ 420.000 após derrota dos Seahawks por shutout" , a concessionária realizou uma promoção para pagar US$ 35.000 a doze vencedores caso os Seahawks vencessem os Giants por shutout na partida da semana 15, realizada em 15 de dezembro de 2013. O artigo afirma ainda que a concessionária pagou US$ 7.000 por uma apólice de seguro para cobrir o pagamento caso isso de fato ocorresse.
Com base em todos os jogos da NFL das temporadas de 1983 a 2012, um lado específico de cada partida não marcou pontos. No entanto, como azarão por sete pontos, em um jogo com uma previsão de pontos acima da média, eu diria que a probabilidade dos Giants não marcarem pontos era maior do que a média. A previsão de pontos para aquele jogo era de 41. Vamos fazer um pouco de álgebra para calcular o número esperado de pontos dos Giants.
Deixar:
s = Pontos dos Seahawks
g = Pontos dos Giants
Sabemos que s+g=41 e s=g+7, com base na diferença de pontos e no total de pontos (acima/abaixo).
Substituindo a segunda equação na primeira:
(g+7) + g = 41
2g + 7 = 41
2g = 34
g = 17
Em seguida, vamos analisar a probabilidade de um shutout com base no número estimado de pontos de cada equipe, considerando as temporadas de 1983 a 2012. Ignorei as linhas em que o tamanho da amostra era zero.
Probabilidade de não marcar gols
| Estimado Pontos | Tamanho da amostra | Desligamentos | Razão |
|---|---|---|---|
| 5,25 | 1 | 0 | 0,0% |
| 6,50 | 1 | 0 | 0,0% |
| 7,75 | 1 | 0 | 0,0% |
| 8,00 | 1 | 0 | 0,0% |
| 8,25 | 3 | 0 | 0,0% |
| 8,50 | 2 | 0 | 0,0% |
| 8,75 | 2 | 0 | 0,0% |
| 9,00 | 2 | 0 | 0,0% |
| 9,50 | 4 | 0 | 0,0% |
| 9,75 | 6 | 1 | 16,7% |
| 10,00 | 10 | 1 | 10,0% |
| 10,25 | 7 | 0 | 0,0% |
| 10,50 | 14 | 2 | 14,3% |
| 10,75 | 7 | 1 | 14,3% |
| 11:00 | 13 | 1 | 7,7% |
| 11,25 | 21 | 1 | 4,8% |
| 11,50 | 22 | 3 | 13,6% |
| 11,75 | 23 | 1 | 4,3% |
| 12h00 | 34 | 2 | 5,9% |
| 12,25 | 36 | 7 | 19,4% |
| 12,50 | 41 | 3 | 7,3% |
| 12,75 | 39 | 4 | 10,3% |
| 13:00 | 55 | 1 | 1,8% |
| 13,25 | 58 | 5 | 8,6% |
| 13,50 | 78 | 1 | 1,3% |
| 13,75 | 89 | 5 | 5,6% |
| 14:00 | 92 | 4 | 4,3% |
| 14,25 | 108 | 7 | 6,5% |
| 14,50 | 117 | 8 | 6,8% |
| 14,75 | 141 | 7 | 5,0% |
| 15h00 | 160 | 7 | 4,4% |
| 15,25 | 160 | 7 | 4,4% |
| 15,50 | 213 | 7 | 3,3% |
| 15,75 | 198 | 11 | 5,6% |
| 16:00 | 206 | 6 | 2,9% |
| 16,25 | 221 | 12 | 5,4% |
| 16,50 | 241 | 10 | 4,1% |
| 16,75 | 273 | 7 | 2,6% |
| 17:00 | 306 | 8 | 2,6% |
| 17,25 | 305 | 8 | 2,6% |
| 17,50 | 306 | 10 | 3,3% |
| 17,75 | 323 | 4 | 1,2% |
| 18h00 | 299 | 8 | 2,7% |
| 18,25 | 332 | 8 | 2,4% |
| 18,50 | 309 | 9 | 2,9% |
| 18.75 | 307 | 7 | 2,3% |
| 19h00 | 356 | 8 | 2,2% |
| 19,25 | 389 | 5 | 1,3% |
| 19,50 | 361 | 5 | 1,4% |
| 19,75 | 343 | 6 | 1,7% |
| 20,00 | 402 | 8 | 2,0% |
| 20,25 | 379 | 6 | 1,6% |
| 20,50 | 359 | 3 | 0,8% |
| 20,75 | 353 | 5 | 1,4% |
| 21h00 | 344 | 1 | 0,3% |
| 21,25 | 317 | 3 | 0,9% |
| 21,50 | 341 | 2 | 0,6% |
| 21,75 | 331 | 1 | 0,3% |
| 22h00 | 369 | 1 | 0,3% |
| 22,25 | 336 | 0 | 0,0% |
| 22,50 | 316 | 2 | 0,6% |
| 22,75 | 280 | 3 | 1,1% |
| 23h00 | 311 | 1 | 0,3% |
| 23,25 | 290 | 3 | 1,0% |
| 23,50 | 279 | 1 | 0,4% |
| 23,75 | 255 | 1 | 0,4% |
| 24,00 | 246 | 1 | 0,4% |
| 24,25 | 219 | 0 | 0,0% |
| 24,50 | 230 | 2 | 0,9% |
| 24,75 | 230 | 1 | 0,4% |
| 25,00 | 212 | 2 | 0,9% |
| 25,25 | 207 | 0 | 0,0% |
| 25,50 | 176 | 1 | 0,6% |
| 25,75 | 154 | 0 | 0,0% |
| 26,00 | 154 | 1 | 0,6% |
| 26,25 | 113 | 0 | 0,0% |
| 26,50 | 137 | 0 | 0,0% |
| 26,75 | 122 | 0 | 0,0% |
| 27,00 | 95 | 0 | 0,0% |
| 27,25 | 98 | 0 | 0,0% |
| 27,50 | 83 | 0 | 0,0% |
| 27,75 | 81 | 0 | 0,0% |
| 28,00 | 82 | 0 | 0,0% |
| 28,25 | 55 | 1 | 1,8% |
| 28,50 | 56 | 0 | 0,0% |
| 28,75 | 51 | 0 | 0,0% |
| 29,00 | 48 | 0 | 0,0% |
| 29,25 | 34 | 0 | 0,0% |
| 29,50 | 24 | 0 | 0,0% |
| 29,75 | 25 | 0 | 0,0% |
| 30,00 | 24 | 0 | 0,0% |
| 30,25 | 21 | 0 | 0,0% |
| 30,50 | 18 | 0 | 0,0% |
| 30,75 | 23 | 0 | 0,0% |
| 31,00 | 16 | 0 | 0,0% |
| 31,25 | 15 | 0 | 0,0% |
| 31,50 | 8 | 0 | 0,0% |
| 31,75 | 3 | 0 | 0,0% |
| 32,00 | 6 | 0 | 0,0% |
| 32,25 | 7 | 0 | 0,0% |
| 32,50 | 6 | 0 | 0,0% |
| 32,75 | 3 | 0 | 0,0% |
| 33,00 | 4 | 0 | 0,0% |
| 33,25 | 6 | 0 | 0,0% |
| 33,50 | 5 | 0 | 0,0% |
| 34,75 | 4 | 0 | 0,0% |
| 35,00 | 2 | 0 | 0,0% |
| 35,50 | 1 | 0 | 0,0% |
| 36,00 | 2 | 0 | 0,0% |
| 36,25 | 1 | 0 | 0,0% |
| 36,50 | 1 | 0 | 0,0% |
| 37,25 | 1 | 0 | 0,0% |
| 37,75 | 2 | 0 | 0,0% |
| 42,25 | 1 | 0 | 0,0% |
Os próximos passos são muito complexos para explicar aqui, mas desenvolvi uma fórmula para a probabilidade de um shutout, dado o número estimado de pontos.
p = Pontos estimados.
x = 1,562545 - 0,302485 * p
probabilidade de shutout = e x /(1+e x )
O gráfico a seguir mostra a probabilidade real e estimada de uma partida sem sofrer gols por uma diferença de 14 a 22 pontos.
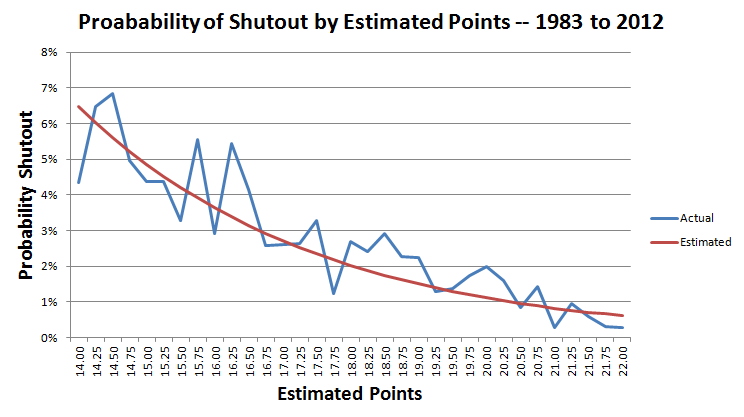
Na partida em questão, esperava-se que os Giants marcassem 17 pontos.
Utilizando a fórmula acima da tabela:
x = 1,562545 -0,302485 * 17 = -3,579706
Probabilidade de shutout = exp(-3,579706)/( exp(-3,579706)+1) = 2,71%. Para ser exato, 0,0271275.
Considerando que a concessionária teria que pagar US$ 420.000 caso o Giants perdesse por 4 a 0, o custo justo do seguro seria de US$ 420.000 × 0,0271275 = US$ 11.394. Normalmente, as seguradoras que oferecem promoções incomuns como essa dobram o custo justo, então eu esperaria um prêmio de US$ 22.788. Portanto, o prêmio de US$ 7.000 pago pela concessionária foi uma pechincha. Supondo que o chefe revise os cálculos, eu não gostaria de estar no lugar de quem calculou esse prêmio de US$ 7.000.
Essa questão foi levantada e discutida no meu fórum no Wizard of Vegas .
Qual é a prova de que não existe um maior número primo?
Vamos supor, por um minuto, que exista um maior número primo. Podemos numerar os números primos como p1=2, p2=3, p3=5, p4=7, ... pL = maior número primo.
Agora vamos definir o número x = p1*p2*p3*p4*...*pL + 1.
Um número primo significa que nenhum outro número primo menor o divide exatamente.
Se dividirmos p1, p2, p3, ... pL por x, obteremos um resto de 1 todas as vezes.
Você poderia argumentar que talvez um primo maior que pL divida x exatamente. Sim, mas então você teria encontrado um primo maior que o chamado maior primo. Caso contrário, x se tornaria um novo maior primo, provando a conjectura inicial da existência de um maior primo por contradição.
Essa pergunta foi feita e discutida no meu fórum no Wizard of Vegas .
Você concorda com o artigo intitulado "A matemática diz que você deve comprar um bilhete da Mega Millions agora mesmo" no Business Insider?
Não, eu discordo. Trata-se de uma reportagem péssima e o Business Insider deveria se envergonhar disso.
Para começar, o artigo foi publicado em 17 de dezembro de 2013, antes do sorteio de US$ 636 milhões naquela noite. Vamos analisar os cálculos para avaliar o valor de um bilhete de US$ 1. A tabela a seguir mostra a probabilidade e o retorno esperado de todos os resultados possíveis para o prêmio de US$ 636 milhões, antes de considerar fatores como a multa por pagamento único, impostos e a divisão do prêmio. As três maiores probabilidades estão em notação científica porque os números são muito pequenos.
Mega Millions - Prêmio acumulado de US$ 636 milhões
| Pegar | Mega Bola | Paga | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|---|
| 5 | Sim | $ 636.000.000 | 1 | 3,86E-09 | 2,456634 |
| 5 | Não | US$ 1.000.000 | 14 | 5,41E-08 | 0,054077 |
| 4 | Sim | $ 5.000 | 350 | 1,35E-06 | 0,006760 |
| 4 | Não | $ 500 | 4.900 | 0,000019 | 0,009463 |
| 3 | Sim | $ 50 | 24.150 | 0,000093 | 0,004664 |
| 3 | Não | $ 5 | 338.100 | 0,001306 | 0,006530 |
| 2 | Sim | $ 5 | 547.400 | 0,002114 | 0,010572 |
| 1 | Sim | $ 2 | 4.584.475 | 0,017708 | 0,035416 |
| 0 | Sim | $ 1 | 12.103.014 | 0,046749 | 0,046749 |
| Perdedor | $0 | 241.288.446 | 0,932008 | 0,000000 | |
| Total | 258.890.850 | 1.000000 | 2,630865 | ||
Isso mostra que um ingresso de US$ 1 renderá US$ 2,630864. Após deduzir o dólar que custou o ingresso, o lucro esperado é de US$ 1,630864. O Business Insider recebe US$ 1,632029. Uma diferença de 0,001164, mas nada significativo.
No entanto, existem três fatores que reduzem significativamente o valor:
- A multa em parcela única.
- Impostos.
- Partilha do jackpot.
Vamos analisá-los um de cada vez.
Os grandes prêmios progressivos de loteria geralmente são pagos na forma de uma anuidade de cerca de 30 anos, incluindo a Mega Millions. Se o ganhador quiser o dinheiro todo de uma vez, o que a maioria deseja, ele terá que aceitar uma redução significativa. Isso é justo, pois um dólar hoje vale mais do que um dólar no futuro. No caso do sorteio de 17 de dezembro de 2013, o valor total do prêmio foi reduzido para US$ 347,6 milhões, ou 54,65% do prêmio anunciado.
Em seguida, vamos analisar os impostos. A alíquota máxima do imposto de renda federal é de 39,6%. Os impostos estaduais variam de 0% a 12,3%, então vamos considerar uma média de 6%. Após deduzir 45,6% em impostos, restam US$ 189,1 milhões.
Agora vem a parte mais complicada: a divisão do prêmio principal. Vale ressaltar que, a partir do sorteio de 22 de outubro de 2013, a Mega Millions mudou as regras para um formato 75-15, no qual são sorteados cinco números de 1 a 75 e, em seguida, um número de um conjunto separado de 1 a 15. Isso reduziu as chances de ganhar para 1 em 258.890.850, evidentemente em um esforço para aumentar os prêmios principais. Analisando apenas os 17 sorteios desde então, usando dados de prêmios e vendas do LottoReport.com , constatei uma relação exponencial entre o tamanho do prêmio principal e a demanda. Descobri o mesmo para a loteria Powerball , aliás. Usando regressão exponencial, minha fórmula para o total de bilhetes vendidos (em milhões) é 12,422 × exp(0,0052 × j), onde j é o tamanho do prêmio principal (em milhões). Por exemplo, para um prêmio de US$ 636 milhões, as vendas esperadas seriam de 12,422 * exp(0,0052*636) = 339,2 (milhões). As vendas reais foram de US$ 337 milhões, então bem próximas.
Com base na venda real de 336.545.306 bilhetes, podemos esperar 336.545.306/258.890.850 = 1.300 vencedores. A questão pertinente é: se você ganhar, com quantas outras pessoas você pode esperar dividir o prêmio? Isso é facilmente respondido observando a distribuição de Poisson. Dada uma média de 1,3 vencedores, a probabilidade de haver exatamente x vencedores é exp(1,3)×1,3 x /fact(x). A tabela a seguir mostra a probabilidade de haver de 0 a 10 outros vencedores, sua parte do prêmio em cada caso e a parte esperada, supondo que você ganhe.
A participação esperada no prêmio principal é de 1,3 outros vencedores em média.
| Outros vencedores | Probabilidade | Compartilhamento do prêmio principal | participação esperada |
|---|---|---|---|
| 10 | 0,000001 | 0,090909 | 0,000000 |
| 9 | 0,000008 | 0,100000 | 0,000001 |
| 8 | 0,000055 | 0,111111 | 0,000006 |
| 7 | 0,000339 | 0,125000 | 0,000042 |
| 6 | 0,001827 | 0,142857 | 0,000261 |
| 5 | 0,008431 | 0,166667 | 0,001405 |
| 4 | 0,032429 | 0,200000 | 0,006486 |
| 3 | 0,099786 | 0,250000 | 0,024946 |
| 2 | 0,230283 | 0,333333 | 0,076761 |
| 1 | 0,354295 | 0,500000 | 0,177148 |
| 0 | 0,272545 | 1.000000 | 0,272545 |
| Total | 1.000000 | 0,559602 |
A célula inferior direita mostra que você pode esperar ficar com 55,96% do dinheiro, e os outros 44,04% irão para aqueles outros vencedores com quem você terá que dividir.
Agora, nosso prêmio acumulado de US$ 636 milhões caiu para US$ 189,1 × 55,96% = US$ 105,8 milhões. Vejamos como fica a tabela de retorno com esse valor como prêmio acumulado.
Mega Millions -- Prêmio acumulado de US$ 105,8 milhões
| Pegar | Mega Bola | Paga | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|---|
| 5 | Sim | US$ 105.800.000 | 1 | 3,86E-09 | 0,408666 |
| 5 | Não | US$ 1.000.000 | 14 | 5,41E-08 | 0,054077 |
| 4 | Sim | $ 5.000 | 350 | 1,35E-06 | 0,006760 |
| 4 | Não | $ 500 | 4.900 | 0,000019 | 0,009463 |
| 3 | Sim | $ 50 | 24.150 | 0,000093 | 0,004664 |
| 3 | Não | $ 5 | 338.100 | 0,001306 | 0,006530 |
| 2 | Sim | $ 5 | 547.400 | 0,002114 | 0,010572 |
| 1 | Sim | $ 2 | 4.584.475 | 0,017708 | 0,035416 |
| 0 | Sim | $ 1 | 12.103.014 | 0,046749 | 0,046749 |
| Perdedor | $0 | 241.288.446 | 0,932008 | 0,000000 | |
| Total | 258.890.850 | 1.000000 | 0,582898 | ||
A célula inferior direita mostra um retorno esperado de 58,29%. Em outras palavras, seu investimento de US$ 1 pode render cerca de 58 centavos, resultando em uma perda esperada, ou vantagem da casa, de aproximadamente 42%. Isso soa como um bom argumento para comprar um bilhete?
Segundo o artigo, "Portanto, desde que sejam vendidos menos de 730 milhões de bilhetes, uma situação bastante provável neste momento, o valor esperado de um bilhete deverá ser positivo, e por isso você deve considerar comprar um bilhete da Mega Millions hoje."
As vendas foram bem inferiores a 730 milhões e, mesmo assim, o produto representou um péssimo negócio. No entanto, para sermos justos, o artigo prosseguiu dizendo o seguinte:
"Tenha em mente que existem muitas ressalvas a esta análise. Os impostos provavelmente afetarão seus ganhos esperados de forma bastante severa — o governo federal ficará com cerca de 40%, e seu estado de residência poderá cobrar de 0% a cerca de 13%."
Muita gente tem comprado bilhetes, e como discutido acima, isso aumentará consideravelmente as chances de empate e a consequente redução do prêmio." — Business Insider
Essas são ressalvas muito importantes! Elas não deveriam ser mencionadas apenas de passagem no final, mas sim levadas em consideração na análise desde o início.
Embora você não tenha perguntado, a matemática me diz que você nunca deveria jogar na Mega Millions. Dada a demanda exponencial por bilhetes, baseada no tamanho do prêmio, acredito que o momento ideal para jogar seja quando o prêmio chega a US$ 545 milhões. Com prêmios maiores que isso, você terá que dividi-lo com muitos outros vencedores. Nesse valor, o jogador pode esperar um retorno de 60,2%, ou uma perda de 39,8%. É o melhor que se pode esperar.
Para concluir, não, eu discordo da Business Insider por enganar os leitores com um título sensacionalista e não fazer uma análise adequada sobre impostos e a divisão de prêmios da loteria.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .


