Pergunte ao Mago #321
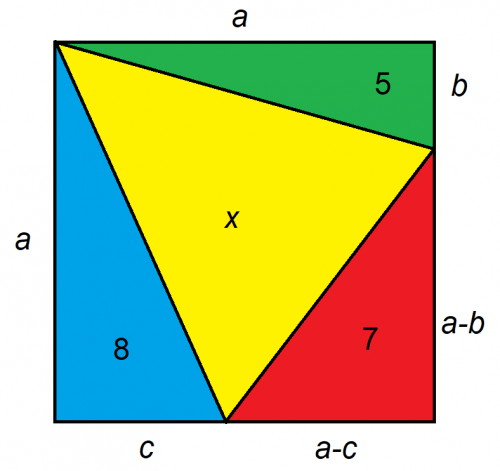
Dado que a figura maior é um quadrado, qual é a área de x?
A chave para problemas como este está na sua formulação. Recomendo tentar simplificar o problema ao máximo possível, reduzindo-o ao mínimo de incógnitas. Neste caso, podemos expressar as distâncias desconhecidas no quadrado em apenas três, da seguinte forma:
É mais fácil lidar com retângulos do que com triângulos. Dado que sabemos a área de três triângulos, podemos dobrar o tamanho e dobrar as áreas. Isso nos dá:
- ab=10
- ac=16
- (ab)(ac)=14
Vamos fatorar (ab)(ac):
a² - ab - ac + bc = 14
a 2 - 10 - 16 + bc = 14
(1) a² + bc = 40
Vamos expressar b e c em termos de a, para reduzir isso a uma única variável:
b = 10/a
c = 16/a
Substituindo esses valores para b e c na equação (1):
a² + (10/a)*(16/a) = 40
a² + 160/ a² = 18
Em seguida, vamos eliminar esse 2 do denominador multiplicando tudo por 2 .
a⁴ + 160 = 40* a²
a₄ - 40* a₂ + 160 = 0
Vamos definir uma nova variável y = a 2
y² - 18y + 32 = 0
Em seguida, vamos resolver para y usando a fórmula quadrática:
y = (40 +/- sqrt(1600-640))/2
y = (40 +/- sqrt(960))/2
y = (40 +/- 8*sqrt(15))/2
y = 20 +/- 4*sqrt(15)
A área do quadrado inteiro é a 2 , que convenientemente é igual a y. Da equação acima, se o +/- for negativo, então y = apx 4,5081, o que está obviamente errado, já que sabemos que a área é pelo menos 20, sem nem mesmo incluir x. Portanto, a área do quadrado deve ser 20 + 4*sqrt(15).
Os três triângulos que nos foram dados têm uma área de 5+7+8=20. Subtraindo isso da área total do quadrado, obtemos a área de x: 20 + 4*sqrt(15) - 20 = 4*sqrt(15) = aproximadamente 15,4919.
Essa questão é levantada e discutida no meu fórum no Wizard of Vegas .

Reparem na minha camiseta nesta foto. A caixa do cinema elogiou-a quando fui ver "Uncut Gems" . Agradeci-lhe torturando-a com este problema, só que com triângulos de áreas 2, 3 e 4. Depois do filme, fui ver como ela estava e ela ainda não tinha resolvido, mas parecia estar a tentar. Então, escrevi a seguinte solução para ela no bar Suncoast. Ela pareceu gostar bastante. Acho que essa jovem vai longe na vida.
Em relação à loteria, existe um "ponto de inflexão" no tamanho do prêmio principal em loterias interestaduais (Powerball, Mega Millions) a partir do qual é mais provável que o prêmio seja dividido do que haja um único vencedor? Se sim, qual é esse valor?
Não vou entrar em detalhes matemáticos, mas aqui estão os pontos do jackpot onde a probabilidade de haver vários vencedores é a mesma que a de haver apenas um:
- PowerBall: US$ 975 milhões
- Mega Millions: US$ 1,65 bilhão
Embora você não tenha perguntado, aqui estão os prêmios principais onde a probabilidade de haver pelo menos um vencedor é igual à probabilidade de não haver nenhum (50%).
- PowerBall: US$ 704 milhões
- Mega Millions: US$ 867 milhões
Essa questão foi levantada e discutida no meu fórum, Wizard of Vegas .
- Em uma prisão há 12 prisioneiros, cada um numerado de 1 a 12.
- O carcereiro instala 12 caixas, cada uma numerada de 1 a 12.
- Dentro das 12 caixas estão os números de 1 a 12, dispostos aleatoriamente, um em cada caixa.
- Cada prisioneiro, individualmente, poderá abrir seis caixas de sua escolha. Ele poderá escolher e abri-las uma de cada vez.
- O objetivo de cada prisioneiro é encontrar seu próprio número dentro de uma caixa, dentre as seis opções disponíveis. Se ele conseguir, diz-se que essa pessoa sobrevive.
- Se um prisioneiro não encontrar o seu próprio número, considera-se que todo o grupo falhou e será imediatamente conduzido a um pelotão de fuzilamento.
- Se um prisioneiro sobreviver, ele deverá recolocar os números em suas caixas originais para o próximo prisioneiro.
- Os prisioneiros não podem observar outros jogadores nem se comunicar depois que o jogo começar.
- Antes de começar, todo o grupo pode colaborar na elaboração de uma estratégia. O objetivo é que todos os 12 prisioneiros sobrevivam (ou seja, encontrem seu próprio número dentro de uma caixa).
Qual deve ser a estratégia deles para maximizar a probabilidade de sobrevivência e qual é essa probabilidade?
Assim como em um jogo de Amigo Secreto, haverá ciclos ligando um número a outro. Com 12 prisioneiros, pode haver de 1 a 12 ciclos. Se nenhum ciclo for maior que seis, então todos os prisioneiros eventualmente encontrarão seu número. A grande questão é: qual a probabilidade de nenhum ciclo ser maior que seis? Vamos inverter a lógica e encontrar o número de combinações de ciclos com tamanho igual ou superior a 7.
Solução para 12 prisioneiros
| Laços | Combinações | Probabilidade |
|---|---|---|
| 12 | 39.916.800 | 0,083333 |
| 11,1 | 43.545.600 | 0,090909 |
| 10,2 | 23.950.080 | 0,050000 |
| 10,1,1 | 23.950.080 | 0,050000 |
| 9,3 | 17.740.800 | 0,037037 |
| 9,2,1 | 26.611.200 | 0,055556 |
| 9,1,1,1 | 8.870.400 | 0,018519 |
| 8,4 | 14.968.800 | 0,031250 |
| 8,3,1 | 19.958.400 | 0,041667 |
| 8,2,2 | 7.484.400 | 0,015625 |
| 8,2,1,1 | 14.968.800 | 0,031250 |
| 8,1,1,1,1 | 2.494.800 | 0,005208 |
| 7,5 | 13.685.760 | 0,028571 |
| 7,4,1 | 17.107.200 | 0,035714 |
| 7,3,2 | 11.404.800 | 0,023810 |
| 7,3,1,1 | 11.404.800 | 0,023810 |
| 7,2,2,1 | 8.553.600 | 0,017857 |
| 7,2,1,1,1 | 5.702.400 | 0,011905 |
| 7,1,1,1,1,1 | 570.240 | 0,001190 |
| Total | 312.888.960 | 0,653211 |
A tabela a seguir mostra as fórmulas para as combinações na tabela acima.
Fórmulas de combinação
| Laços | Combinações | Fórmula |
|---|---|---|
| 12 | 39916800 | =FATO(11) |
| 11,1 | 43545600 | =COMBIN(12,11)*FACT(10) |
| 10,2 | 23950080 | =COMBIN(12,10)*FACT(9) |
| 10,1,1 | 23950080 | =COMBIN(12,10)*FACT(9) |
| 9,3 | 17740800 | =COMBIN(12,9)*FACT(8)*FACT(2) |
| 9,2,1 | 26611200 | =COMBIN(12,9)*COMBIN(3,2)*FATO(8) |
| 9,1,1,1 | 8870400 | =COMBIN(12,9)*FACT(8) |
| 8,4 | 14968800 | =COMBIN(12,8)*FACT(7)*FACT(3) |
| 8,3,1 | 19958400 | =COMBIN(12,8)*COMBIN(4,3)*FATO(7)*FATO(2) |
| 8,2,2 | 7484400 | =COMBIN(12,8)*COMBIN(4,2)*FATO(7)/2 |
| 8,2,1,1 | 14968800 | =COMBIN(12,8)*COMBIN(4,2)*FATO(7) |
| 8,1,1,1,1 | 2494800 | =COMBIN(12,8)*FACT(7) |
| 7,5 | 13685760 | =COMBIN(12,7)*FACT(6)*FACT(4) |
| 7,4,1 | 17107200 | =COMBIN(12,7)*5*FACT(6)*FACT(3) |
| 7,3,2 | 11404800 | =COMBIN(12,7)*COMBIN(5,3)*FATO(6)*FATO(2) |
| 7,3,1,1 | 11404800 | =COMBIN(12,7)*COMBIN(5,3)*FATO(6)*FATO(2) |
| 7,2,2,1 | 8553600 | =COMBIN(12,7)*COMBIN(5,2)*COMBIN(3,2)*FATO(6)/2 |
| 7,2,1,1,1 | 5702400 | =COMBIN(12,7)*COMBIN(5,2)*FATO(6) |
| 7,1,1,1,1,1 | 570240 | =COMBIN(12,7)*FACT(6) |
Na célula inferior direita da primeira tabela, existem 312.888.960 combinações perdedoras. O número total de maneiras de organizar os números é 12! = 479.001.600. Portanto, a probabilidade de falha é 312.888.960 / 479.001.600 = 65,32%. Logo, a probabilidade de sucesso é 100% - 65,32% = 34,68%.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
Olá. Tenho um cupom que me permite fazer uma mão de 22. Posso guardar o cupom até conseguir a minha primeira mão de 22. Ele não se aplica a combinações duplas ou divididas. Qual é o valor disso?
Uma resposta rápida é o valor da aposta máxima permitida. Basta esperar por um 22 e então jogar, resultando em sair da mesa com uma unidade extra.
Uma resposta mais rigorosa deveria levar em conta o custo de esperar por esse 22. Isso é algo que eu não sei exatamente, mas posso estimar.
O custo para o jogador da regra de empate do dealer no 22 é de 6,91%. No entanto, o dealer chegará a 22 mais vezes do que isso, porque o jogador não se importará se estourar primeiro. Dependendo das regras, o jogador estourará cerca de 15,7% das vezes. Se assumirmos que isso não está correlacionado com a probabilidade de o dealer estourar (o que não está), então a probabilidade de o dealer estourar é de 6,91%/(1,0-0,157) = 8,2%.
Sei que é uma estimativa aproximada, mas vamos assumir que a probabilidade do jogador tirar 22 seja a mesma. Sei que o dealer vai estourar mais vezes do que o jogador, mas este cupom também não conta após uma divisão, então vamos considerar que esses fatores se compensam. Portanto, se o jogador tirar 22 em 8,2% das mãos, ele tirará 22 uma vez a cada 1/0,082 = 12,2 mãos em média.
Digamos que a vantagem da casa no jogo base seja de 0,75%. O custo de jogar 12,2 mãos com essa vantagem da casa é 12,2 * 0,0075 = 0,0915. Portanto, subtraindo isso do valor unitário, obtemos um valor para o cupom de 1,0 - 0,0915, que corresponde a cerca de 91% do valor nominal.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .