Pergunte ao Mago #425

Q: <p>Sua tarefa é cortar o triângulo abaixo em duas partes de áreas iguais com um corte vertical (ou seja, paralelo ao lado a). Onde você deve fazer o corte? </p><p></p><img alt="" height="354" src="/media/content_images/1610/ask-the-wizard-425-q.png" width="600" />

<div><button onclick='var btn = this; var div = btn.parentNode.childNodes[1]; if (div.style.display != "block") { div.style.display="block"; } else { div.style.display="none"; }' style='padding:2px 4px;'>Resposta</button><div class='spoiler'> O corte deve ser feito a partir de b/sqrt(2) do lado mais à direita do triângulo. Observe que a altura não importa. </div></div><p></p><p> Aqui está minha <a href="/pdf/2083/ask-the-wizard-425.pdf">solução</a> (PDF).</p><p> Essa pergunta é feita e discutida no meu fórum, <a href="https://wizardofvegas.com/forum/questions-and-answers/math/34502-easy-math-puzzles/104/#post964901" target="_blank">Wizard of Vegas</a> .</p>

Q: <p>Na <a href="wizardofodds.com/ask-the-wizard/424/">coluna &quot;Pergunte ao Mago&quot; nº 424,</a> alguém perguntou: &quot;Uma régua de um metro é cortada em dois lugares aleatórios. Qual é a área esperada do menor dos três pedaços criados?&quot; Minha pergunta é: qual seria a resposta para c cortes aleatórios?</p>

<div><button onclick='var btn = this; var div = btn.parentNode.childNodes[1]; if (div.style.display != "block") { div.style.display="block"; } else { div.style.display="none"; }' style='padding:2px 4px;'>Resposta</button><div class='spoiler'>1/(c+1)^2</div></div><p></p><p> Aqui está <a href="/pdf/2082/ask-the-wizard-425b.pdf">minha solução</a> (PDF).</p><p> Este problema é abordado e discutido no meu fórum, <a href="https://wizardofvegas.com/forum/questions-and-answers/math/34502-easy-math-puzzles/104/" target=_blank>Wizard of Vegas</a> .</p>

Sua tarefa é cortar o triângulo abaixo em duas partes de áreas iguais com um corte vertical (ou seja, paralelo ao lado a). Onde você deve fazer o corte?

anônimo

O corte deve ser feito a partir de b/sqrt(2) do lado mais à direita do triângulo. Observe que a altura não importa.

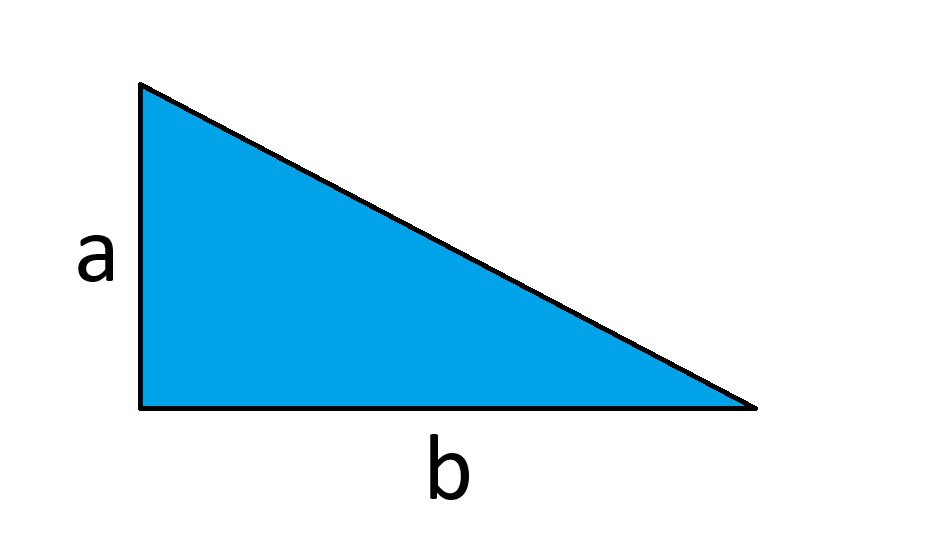
Aqui está minha solução (PDF).

Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .

Na coluna "Pergunte ao Mago" nº 424, alguém perguntou: "Uma régua de um metro é cortada em dois lugares aleatórios. Qual é a área esperada do menor dos três pedaços criados?" Minha pergunta é: qual seria a resposta para c cortes aleatórios?

anônimo

1/(c+1)^2

Aqui está minha solução (PDF).

Este problema é abordado e discutido no meu fórum, Wizard of Vegas .

De quantas maneiras você pode colocar seis bolas diferentes em três caixas idênticas?

anônimo

A resposta é 122

A parte complicada deste problema é que as caixas são idênticas. Se fossem diferentes, a resposta seria facilmente encontrada como 3 ⁶ = 729.

Vamos numerar as bolas de A a F. Comece colocando a bola A em qualquer caixa.

Primeiro, digamos que você coloque a bola B em uma das duas caixas vazias restantes. A partir daí, as três caixas são diferentes porque contêm bolas diferentes, incluindo uma que ainda está vazia. O número de maneiras de colocar as outras quatro bolas é 3 ^{× 4} = 81.

Em segundo lugar, digamos que você coloque a bola B na mesma caixa que a bola A e a bola C em uma das caixas vazias. A partir daí, as três caixas são diferentes porque contêm bolas diferentes, incluindo uma que ainda está vazia. O número de maneiras de colocar as outras três bolas é 3 ^{× 3} = 27.

Terceiro, digamos que você coloque as bolas B e C na mesma caixa que as bolas A e D em uma das caixas vazias. A partir daí, as três caixas são diferentes porque contêm bolas diferentes, incluindo uma que ainda está vazia. O número de maneiras de colocar as outras duas bolas é ^3² = 9.

Em quarto lugar, digamos que você coloque as bolas B, C e D na mesma caixa que as bolas A e E em uma das caixas vazias. A partir daí, as três caixas são diferentes porque contêm bolas diferentes, incluindo uma que ainda está vazia. O número de maneiras de colocar a outra bola é 3 ^{× 1} = 3.

Quinto, digamos que você coloque as bolas B a E na mesma caixa que a bola A e F em uma das caixas vazias. Não sobram bolas, então só há uma maneira de as bolas A a E estarem em uma caixa e F em outra.

Sexto e último ponto: existe apenas um caminho para todas as bolas na mesma caixa.

Portanto, a resposta é ^3⁴ + ^3³ + ^3² + ^3¹ + 2 = 122.

Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .

Qual é o total médio final do dealer no blackjack, assumindo que ele não faça blackjack nem ultrapasse 25%?

anônimo