Probabilidade - Cartões
Eu estava jogando bacará online e, em 75 mãos, o banqueiro ganhou 52 e o jogador 23. Essa diferença é de 29. Qual é a probabilidade disso acontecer?
Primeiro, vou assumir que você não está contando empates. Em outras palavras, você se refere a 75 apostas resolvidas. Seria muito improvável que 75 mãos fossem jogadas sem um empate. O número esperado de vitórias do banqueiro em 75 apostas resolvidas é 38,00913745. O desvio padrão é a raiz quadrada do produto de 75, a probabilidade de uma vitória do banqueiro e a probabilidade de uma vitória do jogador. A probabilidade de uma vitória do banqueiro, dado que não houve empate, é 0,506788499 e a probabilidade de uma vitória do jogador é 0,493211501. O desvio padrão é, portanto, 4,329727904. Em seguida, você precisará fazer uma correção de meio ponto para uma distribuição binomial e consultar a estatística Z em uma tabela normal padrão (esta etapa fica a cargo do leitor). A resposta final é que a probabilidade do banqueiro obter 52 ou mais vitórias é 0,0009. Sua pergunta também considerou a possibilidade do banqueiro ganhar 23 vezes ou menos (ou seja, uma diferença de 29 ou mais), o que tem uma probabilidade de 0,0004. Portanto, a resposta final é que a probabilidade de uma diferença de 29 ou mais é de 0,0013, ou 1 em 769.
Ao calcular as combinações de mãos do jogador e do dealer para Caribbean Stud Poker , obtive apenas 3.986.646.103.440, enquanto você obteve 19, etc. Estou com uma diferença exata de um fator de 5. Usei combin (52,5)*combin(47,5). Onde errei? Obrigado e acho seu site excelente.
Obrigado pelo elogio. Você errou por um fator de cinco porque o crupiê pode ter qualquer uma das 5 cartas viradas para cima. Em outras palavras, a ordem importa na mão do crupiê, já que a primeira carta é distribuída virada para cima. A derivação correta do total de combinações é combin(52,5)*47*combin(46,4) = 19.933.230.517.200.
Quais são as probabilidades de tirar três cartas para formar um par e conseguir um full house no pôquer de cinco cartas?
Existem duas maneiras de conseguir um full house nesta situação: (1) comprar uma trinca ou (2) comprar mais uma carta do mesmo tipo e outro par. Vou assumir que você descarta três cartas individuais.
Primeiro, vamos calcular o número de combinações em (1). Há 3 fileiras com apenas 3 naipes restantes (lembre-se de que você descartou 3 singletons) e 9 fileiras com 4 naipes restantes. O número de combinações é, portanto, 3*combin(3,3)+9*combin(4,3) = 3*1 + 9*4 = 39.
Em seguida, vamos calcular o número de combinações sob (2). Restam 2 naipes para adicionar ao par existente. Existem combin (3,2) maneiras de formar um par a partir dos 3 valores com 3 cartas restantes e combin(4,2) maneiras de formar um par a partir dos valores com 4 cartas restantes. Portanto, o total de combinações sob 2 é 2*(3*combin(3,2)+9*combin(4,2)) = 2*(3*3 + 9*6) = 126. O número total de maneiras de organizar um full house é a soma sob (1) e (2), ou 39+126=165. Existem combin(47,3)=16.215 maneiras de organizar as 3 cartas na segunda compra. A probabilidade de tirar uma casa cheia é o número de maneiras de tirar uma casa cheia dividido pelo total de combinações, ou 165/16.215 = 0,0101758, ou cerca de 1 em 98.
Para obter mais informações sobre a função combin(), consulte minha seção sobre probabilidades no pôquer .
Comecei a jogar pôquer com meus amigos uma vez por semana (five-card draw, stud, seven-card stud). Temos sete jogadores na mesa. Parece-me que a probabilidade de formar boas mãos diminui drasticamente devido ao número de jogadores que recebem cartas de um baralho de 52 cartas. Você conhece alguma fórmula matemática que possa me ajudar a entender melhor essa situação?
Não, a probabilidade de receber qualquer mão é a mesma, independentemente do número de outros jogadores na mesa. Uma carta não vista é uma carta não vista, não importa se outro jogador a possui ou se ela ainda está no baralho.
Recentemente me contaram uma história inacreditável! Um amigo me disse que, em um jogo de pôquer amistoso na casa dele, ele e um amigo conseguiram um straight flush natural na mesma mão, sem comprar nenhuma carta! (em uma partida de pôquer de cinco cartas). Acho isso difícil de acreditar e, pelo seu site, calculei que a probabilidade de um straight flush é de aproximadamente 65.000 para 1. Qual seria a probabilidade de dois straight flushes em uma mão com 6 jogadores (sem comprar nenhuma carta)?
Vou dar uma resposta aproximada assumindo que cada jogador recebeu uma mão de um baralho diferente. Isso não deve alterar muito as probabilidades. A probabilidade de um jogador tirar uma sequência de flush, conforme explicado na minha seção sobre probabilidades no pôquer, é de 36/2.598.960. Vamos chamar essa probabilidade de p. A probabilidade de dois jogadores tirarem uma sequência de flush é combin (6,2)*p 2 *(1-p) 4 = 0,0000000028779. Em outras palavras, a probabilidade contra isso acontecer é de 347.477.740 para 1.
Como você calcula as probabilidades separadas de obter: (1) dama alta, (2) rei alto e (3) ás alto no pôquer de três cartas?
Vou calcular primeiro a probabilidade de um rei ser o número máximo de cartas e mostrar brevemente a fórmula para as outras duas. A probabilidade será o número de mãos com rei como carta mais alta dividido pelo número total de mãos. O número de cartas menores que o rei é 11. Uma mão com rei como carta mais alta deve ter duas cartas diferentes dessas cartas. O número de maneiras de organizar 2 dessas 11 cartas é combin (11,2) = 55. No entanto, uma dessas combinações é rei-dama-valete, resultando em uma sequência, então, subtraindo essa combinação, restam 54 que não formam uma sequência. Além disso, existem quatro naipes para cada carta, ou 4³ = 64 combinações possíveis de naipes. Porém, quatro dessas 64 resultam em um flush, então restam 64 - 4 = 60 combinações de naipes. Portanto, o número total de combinações com rei como carta mais alta é 54 * 60 = 3240. Existem um total de combin(52,3)=22.100 combinações possíveis para formar 3 cartas dentre as 52. Portanto, a probabilidade de formar um rei como carta mais alta é 3.240/22.100 = 0,1466063. A probabilidade de formar um ás como carta mais alta é: (combin(12,2)-2)*(4 3 -4)/combin(52,3)=0,1737557. Observe o -2 em vez de -1 devido às sequências A-2-3 e Q-Ka.
A probabilidade de rainha ser a mais alta é: (combin(10,2)-1)*(4 3 -4)/combin(52,3)=0,119457.
Quais são as chances de receber um Royal Flush? E de receber um Royal Flush SEQUENCIAL (em ordem direta ou inversa)?
A probabilidade de qualquer sequência real é o número de sequências reais possíveis, que é quatro (uma para cada naipe), dividido pelo número de maneiras de escolher 5 cartas dentre 52, que é combin (52,5)=2.598.960. Portanto, a resposta é 4/2.598.960 = 0,00000153908, ou 1 em 649.740.
A probabilidade de um royal flush sequencial é igual a (número de naipes) * (número de direções) / (total de permutações de 5 cartas dentre 52) = 4 * 2 / permut (52,5) = 8 / 311.875.200 = 8 / número de possíveis royal flushes, que é quatro (um para cada naipe), vezes o número de direções possíveis dividido pelo número de maneiras de escolher 5 cartas dentre 52, que é permut (52,5) = 311.875.200. Portanto, a resposta é 4/311.875.200 = 0,00000002565, ou 1 em 38.984.400.
Eu gosto de jogar pôquer de mentirosos com notas de dólar. Qual é a probabilidade de sair qualquer combinação de 1, 2, 3, 4 ou 5 números iguais em uma nota? Obrigado. Se eu estiver jogando com 3 pessoas, qual é a probabilidade de sair qualquer número igual?
Primeiramente, permita-me responder à pergunta não formulada sobre a probabilidade de um número específico aparecer n vezes em uma nota aleatória. Uma nota possui 8 dígitos, portanto, a probabilidade de um número específico aparecer n vezes é dada por combin(8,n)* 0,1n *0,9 = 8-n / 10 = 8. A seguir, uma tabela mostrando a probabilidade de um número específico aparecer de 0 a 8.
Probabilidades de Números Específicos no Poker do Mentiroso
| Número | Probabilidade |
|---|---|
| 8 | 0,00000001 |
| 7 | 0,00000072 |
| 6 | 0,00002268 |
| 5 | 0,00040824 |
| 4 | 0,00459270 |
| 3 | 0,03306744 |
| 2 | 0,14880348 |
| 1 | 0,38263752 |
| 0 | 0,43046721 |
| Total | 1.00000000 |
A próxima tabela mostra a probabilidade de cada tipo possível de nota, categorizada pelo número de cada nota de um mesmo tipo (n-of-a-kind). Por exemplo, o número de série 66847680 teria uma nota de três notas do mesmo tipo, um par e três notas individuais, resultando em uma probabilidade de 0,1693440.
Probabilidades gerais no pôquer do mentiroso
| 8 carvalhos | 7 carvalhos | 6 carvalhos | 5 carvalhos | 4 carvalhos | 3 carvalhos | 2 carvalhos | 1 carvalho | Probabilidade |
|---|---|---|---|---|---|---|---|---|
| 1 | 0,0000001 | |||||||
| 1 | 1 | 0,0000072 | ||||||
| 1 | 1 | 0,0000252 | ||||||
| 1 | 2 | 0,0002016 | ||||||
| 1 | 1 | 0,0000504 | ||||||
| 1 | 1 | 1 | 0,0012096 | |||||
| 1 | 3 | 0,0028224 | ||||||
| 2 | 0,0000315 | |||||||
| 1 | 1 | 1 | 0,0020160 | |||||
| 1 | 2 | 0,0015120 | ||||||
| 1 | 1 | 2 | 0,0211680 | |||||
| 1 | 4 | 0,0211680 | ||||||
| 2 | 1 | 0,0020160 | ||||||
| 2 | 2 | 0,0141120 | ||||||
| 1 | 2 | 1 | 0,0423360 | |||||
| 1 | 1 | 3 | 0,1693440 | |||||
| 1 | 5 | 0,0846720 | ||||||
| 4 | 0,0052920 | |||||||
| 3 | 2 | 0,1270080 | ||||||
| 2 | 4 | 0,3175200 | ||||||
| 1 | 6 | 0,1693440 | ||||||
| 8 | 0,0181440 | |||||||
| Total | 1.0000000 | |||||||
carvalho = "de um tipo"
Para mais informações, consulte minha página sobre pôquer de mentirosos .
Com um baralho de 52 cartas, qual a probabilidade de tirar um par de valetes?
Supondo que você compre cinco cartas e conte todas as mãos com exatamente dois valetes, então a probabilidade seria combin(4,2)*combin(48,3)/combin(52,5) = 6*17296/2598960 = 3,99%.
Qual a probabilidade de se obter um par de três cartas no Pai Gow Poker? As chances são menores ou maiores do que as de uma trinca?
Sem contar uma trinca e dois pares, as seguintes são as maneiras de se obter um par de três cartas e o número de combinações possíveis.
Sem curinga: combin(13,3)*10*6 3 *4 =2471040
O curinga usado para competir com um par de ases: combin(12,2)*10*6 2 *4 2 = 380.160
Coringa usado como ás isolado: combin(12,3)*6 3 = 47.520
O número total de combinações é 2.898.720. Isso representa menos da metade das 747.067 combinações possíveis para uma trinca.
De acordo com a sua fórmula, a probabilidade de um Royal Flush é de 4/2.598.960 = 1/649.740. Portanto, se eu estivesse jogando Caribbean Stud um contra um com o dealer, a soma das probabilidades da minha mão e da mão do dealer seria 649.740 * 2 = 1.299.480. Logo, segundo o cálculo, após 1.299.480 mãos, deveriam ocorrer dois Royal Flush. Por favor, me diga se meu entendimento das probabilidades está correto.
Você está certo ao afirmar que, em média, um royal flush ocorre uma vez a cada 649.740 mãos, e que em 1.299.480 mãos o número esperado de royal flushes é 2. No entanto, essa é apenas a média. A cada mão jogada, você não se aproxima mais de conseguir um royal flush. Cada jogo de tentativas independentes possui essa propriedade de ausência de memória, portanto, um royal flush nunca está atrasado.
A probabilidade de se obter zero cartas da realeza em 1.299.480 mãos é de 13,53%.
Olá, sou um jogador assíduo de Pai Gow Poker e notei que seu site tem muitas informações excelentes sobre o jogo. Outro dia, enquanto jogava com um amigo, ele recebeu uma mão com 9 como carta mais alta, que acredito ser a mão mais baixa possível. Em todo o tempo que joguei, só tinha visto isso acontecer uma vez. Cinco mãos depois, ele recebeu exatamente a mesma mão (2-3-4-5-7-8-9). Não conseguimos acreditar e ficamos curiosos para saber qual a probabilidade disso acontecer, então resolvemos perguntar a vocês. Obrigado pelo seu tempo e pelo excelente site.
Existem duas maneiras de organizar as cartas para formar uma mão alta de 9: a que você mencionou e a combinação 2-3-4-6-7-8-9. O número de combinações de naipes sem formar um flush é 4 7 - 4*(combin(7,5)*3^2+6*3+1) = 15.552. Portanto, a probabilidade de uma mão alta de 9 é 2*15.552/combin(53,7) = 31.104/154.143.080, ou 1 em 9.911. Se você jogasse apenas cinco vezes, a probabilidade de obter duas mãos altas de 9 seria de 1 em 9.826.685. Acredito que isso tenha ocorrido por coincidência, e não por falha no gerador de números aleatórios ou na programação do programa.
Minha pergunta diz respeito à vantagem da casa e ao cálculo do elemento de risco no jogo Casino War, de acordo com as regras do Casino Niagara (ou seja, pagamento de 3 para 1 ao aumentar a aposta e perder a aposta inicial). Como você chegou a esses números? Estou tentando calculá-los e estou com dificuldades. Agradeço a ajuda.
Vamos considerar d como o número de baralhos. A probabilidade de um empate na primeira rodada é (4*d-1)/(52*d-1) = 0,073955. A probabilidade de um empate na segunda rodada é 12*4*d/(52*d-2)*(4*d-1)/(52*d-3)+(4*d-2)/(52*d-2)*(4*d-3)/(52*d-3) = 0,073974. Vamos chamar p₁ de probabilidade de empate na primeira rodada e p₂ de probabilidade de empate na segunda rodada. Então, o retorno do jogador é p₁ *(2* p₂ +(1- p₂ )/2*(1-2)) = -0,023301. Multiplicando por -1, obtemos a vantagem da casa de 2,33%. Espero não ter explicado isso muito rapidamente.
Você poderia me explicar como se chega ao número total de combinações possíveis no Caribe, 19.933.230.517.200? Eu segui suas combinações de pôquer de 5 cartas para chegar a 2.598.960. A partir daí, como devo prosseguir? Agradeço antecipadamente.
Você calculou corretamente o número de combinações de jogadores como combin (52,5) = 2.598.960. A partir daí, o dealer pode ter combin(47,5) = 1.533.939 mãos possíveis. Então, qualquer uma das cinco cartas do dealer pode estar virada para cima. Portanto, 2.598.960 * 1.533.959 * 5 = 19.933.230.517.200.
Primeiramente, gostaria de dizer que acho seu site excelente. Já o indiquei para algumas pessoas e espero que elas também o experimentem. Desejo-lhe sucesso contínuo. Também gostei do link para o WinPoker. Gostei tanto do WinPoker que o comprei. É um programa ótimo. Tenho uma dúvida e espero que você possa me ajudar. Estou tentando descobrir quantas vezes cada mão ocorre no Seven-Card Stud. Tenho uma cópia da sua tabela de Seven-Card , mas estou interessado na matemática por trás desses números. Consigo calcular os números do Five-Card, mas o do Seven-Card me deixa perplexo. Gostaria de enviar um arquivo do Excel 2000 com meus cálculos. Também gostaria de saber como calcular o número de sequências em um baralho de 53 cartas com um curinga. Socorro!!!
Obrigado pelas suas amáveis palavras. Concordo que calcular os números para o Seven-Card Stud é difícil. É por isso que eu faço isso no computador. Meu programa analisa todas as combinações possíveis e pontua cada uma. O número de sequências curinga no Pai Gow Poker é 11*(4 4 -4)+10*3*(4 4 -4)=10332. Somando-se às 10200 sequências naturais, o total é 20532.
Entendo quais são as probabilidades de receber um Royal Flush ou um Straight Flush em uma mesa de Caribbean Stud Poker ou Let it Ride e como elas são calculadas. Mas minha dúvida é a seguinte: como um observador externo, qual a probabilidade de ver uma dessas mãos sendo distribuída para um jogador na mesa em uma determinada rodada? Imagino que dependa do número de mãos em jogo... seria simplesmente a probabilidade individual multiplicada pelo número de mãos em jogo? Ou seja, ver um Royal Flush em uma mão específica com 4 jogadores na mesa significa 4 vezes a probabilidade de receber um Royal Flush? Estou um pouco confuso!
Seu método é uma boa aproximação. No entanto, seguindo essa lógica, ao lançar uma moeda, a probabilidade de pelo menos uma pessoa em 3 obter cara seria 3 * 50% = 150%. Assumindo eventos independentes, a probabilidade de pelo menos um sucesso em n tentativas, onde a probabilidade de cada sucesso é p, é 1 - (1 - p) ⁿ . No caso do exemplo do lançamento da moeda, isso seria 1 - 0,5³ = 0,875. No caso de quatro jogadores de Caribbean Stud Poker, a probabilidade de pelo menos um royal flush seria 1 - (1 - 4/2598960) ⁴ = 0,00000615629. Contudo, como todas as cartas são distribuídas do mesmo baralho, os eventos não são independentes. O cálculo se torna muito complexo para determinar a resposta exata, e a aproximação deve estar muito próxima do resultado correto.
Qual a probabilidade de receber um straight flush natural de sete cartas no pôquer pai gow? Trabalho em um cassino e vi isso pela primeira vez em 15 anos. O sortudo ganhou US$ 40.000.
Existem 32 possíveis sequências de flush naturais (4 valores vezes 8 conjuntos possíveis de 7 cartas). Existem combin(53,7) = 154143080 maneiras possíveis de se obter 7 cartas dentre 53. Portanto, a resposta é 32/154143080, ou 1 em 4816971.
Qual a probabilidade de obter duas sequências de flush idênticas (em ambos os valores e naipes) em duas mãos seguidas no Three Card Poker?
A probabilidade de obter um straight flush na primeira mão é 4*12/combin(52,3) = 48/22100 ≈ 0,0022. A probabilidade de a próxima mão ser exatamente igual é 1/22100. Portanto, a resposta é (48/22100)*(1/22100) = 48/488410000, ou seja, 1 em 10.175.208. Isso representa uma probabilidade 1,37 vezes maior do que ganhar na loteria 6/49, que tem uma probabilidade de 1 em 13.983.816.
Em um jogo de bacará com 8 baralhos, qual é a probabilidade de o jogador e o banqueiro obterem um Ás e um 8 de Ouros na mesma mão?
(8 2 /combin(416,2))* (7 2 /combin(414,2)) = 0,00000043, ou 1 em 2308093
Recentemente, presenciei um evento curioso. Estava assistindo a uma partida de pôquer de cinco cartas, onde era possível comprar no máximo duas cartas. Um jogador comprou uma carta e completou um flush de copas. O dealer comprou uma carta e completou um flush de espadas. Naturalmente, o flush do dealer era maior. Havia outros três jogadores na partida. Qual a probabilidade de se ter dois flushes na mesma mão?
Vamos definir a probabilidade de um flush ser obtido na distribuição das cartas ou de um flush de quatro cartas ser completado após a distribuição. Para simplificar, vamos assumir que um jogador completará um par ou uma sequência com quatro cartas para formar um flush. A probabilidade de obter um flush na distribuição das cartas (excluindo sequência/royal flush) é 4*(combin(13,5)-10)/combin(52,5) = 5108/2598960 = 0,0019654. A probabilidade de receber um flush de quatro cartas é 4*3*combin(13,4)*13/combin(52,5) = 111540/2598960 = 0,0429172. A probabilidade de completar o flush na distribuição das cartas é 9/47. Portanto, a probabilidade geral de obter um flush de 4 cartas e completá-lo é 0,0429172 * (9/47) = 0,0082182. Assim, a probabilidade total de um flush é 0,0019654 + 0,0082182 = 0,0101836. A probabilidade de exatamente 2 em 5 jogadores receberem um flush é combin(5,2) * 0,0101836² * (1 - 0,0101836) ³ = 0,001006, ou cerca de 1 em 994.
Preciso saber a probabilidade de alguém conseguir uma quadra em uma mão de Seven Card Stud com cinco jogadores e um baralho de cartas? Espero que você possa me ajudar e agradeço desde já.
Existem combin(52,7) = 133.784.560 maneiras de organizar 7 cartas dentre as 52 restantes. O número de conjuntos de 7 cartas que incluem uma quadra é 13 * combin(48,3) = 224.848. O 13 representa o número de valores possíveis para a quadra e combin(48,3) representa o número de maneiras de escolher 3 cartas dentre as 48 restantes. Portanto, a probabilidade é 224.848 / 133.784.560 = 0,0017, ou 1 em 595.
Ao abrir um novo baralho de cartas, as cartas são dispostas do Ás ao Rei de cada naipe. Qual a probabilidade de pegar um baralho já embaralhado e embaralhá-lo novamente até que ele retorne à ordem original, do Ás ao Rei?
1 em 52 fatorial, ou 1 em 80.658.175.170.943.900.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.
Se dez pessoas receberem duas cartas cada de um mesmo baralho, qual é a probabilidade de que dois jogadores recebam um par de ases?
Primeiro, existem 10*9/2=45 maneiras de escolher 2 jogadores dentre 10. A probabilidade de dois jogadores específicos conseguirem quatro ases é 1/combin(52,4)=1/270725. Portanto, a probabilidade de quaisquer dois jogadores conseguirem um par de ases é 45/270725=0,0001662.
Se sete jogadores receberem sete cartas cada, qual é a probabilidade de pelo menos uma pessoa conseguir um flush de 7 cartas?
A probabilidade de um único jogador conseguir um flush de 7 cartas é 4*combin(13,7)/combin(52,7) = 1 em 19491. A probabilidade de pelo menos um jogador entre 7 conseguir um flush de 7 cartas é de aproximadamente 1 em 2785.
Sei que matematicamente tudo é possível, mas na outra noite, no cassino, acho que presenciei algo que seria uma chance em um bilhão, não que isso nunca aconteça. Eis o que aconteceu: em 40 mãos (40 mãos com 3 cartas cada, cerca de 8 rodadas com 5 jogadores) em uma mesa de "Let it Ride", 3 quadras foram distribuídas. Considerando que uma quadra tem uma probabilidade de aproximadamente 4100 para 1, qual seria a probabilidade de três delas serem distribuídas em 40 mãos? Por favor, respondam, pois isso está me intrigando. Sou fã há muito tempo.
Para simplificar, vamos assumir que cada mão é distribuída de um baralho novo. A probabilidade de uma quadra é 13*48/combin(52,5) = 624/2598960. A probabilidade de exatamente 3 quadras em 40 é combin(40,3)*p 3 *(1-p) 37 = 1 em 7378135, onde p = 624/2598960. Portanto, é mais como uma chance de 1 em 7 milhões.
Primeiramente, gostaria de dizer o quanto admiro seu site e suas habilidades matemáticas. Uso 6 baralhos para distribuir as cartas no blackjack e adicionei 3 curingas por motivos que não vou detalhar agora, mas gostaria de saber qual a probabilidade de distribuir os 3 curingas para um jogador em sequência? Muito obrigado.
De nada, obrigado pelos elogios. A probabilidade de receber 3 curingas seguidos de um sapato com seis baralhos (mais os 3 curingas) é 1/combin(315,3) = 1 em 5.159.805. Outra solução é (3/315)*(2/314)*(1/313).
Qual a probabilidade de distribuir 13 cartas para cada um de quatro jogadores usando um baralho de 52 cartas e todos os quatro jogadores terem uma sequência do Ás ao Dois? As cartas não precisam ser do mesmo naipe.
A resposta é (4 13 /COMBIN(52,13))* (3 13 /COMBIN(39,13))* (2 13 /COMBIN(26,13)) = 1 em 61.204.166.001.
Qual a probabilidade de receber um quatro em vez de uma carta real?
Existem quatro naipes possíveis para um Royal Flush. Existem cinco cartas faltando. A quinta carta pode ser uma de 47 outras cartas. Portanto, existem 4 * 5 * 47 = 940 maneiras de se obter um Royal Flush com quatro cartas. Existem combinações (52, 5) = 2.598.960 combinações no total. Assim, a probabilidade é 940/2.598.960 = 1 em 2.765.
Prezado especialista, imagine que um baralho de 52 cartas seja embaralhado e que 18 dessas 52 cartas sejam retiradas aleatoriamente, sendo divididas em 6 pilhas de 3 cartas cada. Qual é a probabilidade de que uma das pilhas contenha exatamente 3 (dos 4) ases?
A maneira mais fácil de resolver o problema é que a probabilidade de a primeira pilha ter três ases é (4/52)*(3/51)*(2/50) = 1/5525. No entanto, cada pilha tem a mesma probabilidade de ter três ases, então multiplicamos por 6, resultando em 6/5525 = 0,001086.
Qual é a probabilidade de obter todas as cartas com figuras (valete, dama e rei) no jogo de cinco cartas?
(12/52)*(11/51)*(10/50)*(9/49)*(8/48) = 0,00030474, ou cerca de 1 em 3282.
Qual a probabilidade de obter duas quadras em um período de duas horas jogando Let it Ride?
A probabilidade de uma quadra em qualquer mão dada é 13*48/combin(52,5) = 0,0002401. Vamos supor que em duas horas você possa jogar 120 mãos. A probabilidade de exatamente duas quadras seria combin(120,2) × 0,0002401 2 × (1-0,0002401) 118 = 0,000400095 = 1 em 2499,41.
No pôquer de quatro cartas, o que tem maior probabilidade de ser uma sequência ou um flush?
Sem contar as sequências de flush e os royal flushes, a probabilidade de uma sequência é de 1,02% e a de um flush é de 1,04%. Portanto, um flush é ligeiramente mais provável.
Qual é a probabilidade, ao longo de 1 milhão de mãos, de haver uma seca de Royal Flush que se estenda por 200.000 mãos? Estou mais interessado na solução do que na resposta em si.
Não costumo dizer isso, mas tentei por horas e a matemática envolvida era simplesmente incompreensível para mim. Então, recorri ao meu amigo e professor de matemática, Gabor Megyesi. Aqui está a fórmula dele para qualquer problema de "seca".
- Seja p a probabilidade de ganhar uma determinada mão de jogo.
- Seja d a duração da seca.
- Seja n o número de mãos jogadas.
- Defina k=dp e x=np.
- Se k = 1, então a = -1; caso contrário, encontre um valor de a tal que k = -ln(-a)/(1 + a). (a é um número negativo; se k > 1, então -1 < a < 0; se k < 1, então a < -1; e a precisa ser calculado com alta precisão.) [Nota do autor: Este tipo de solução pode ser facilmente encontrado no Excel usando a função Atingir Meta no menu Ferramentas.]
- se k=1 então seja A=2, caso contrário seja A=(1+a)/(1+ak).
- A probabilidade de não haver seca de duração d em n mãos é aproximadamente Ae a x .
Neste problema específico, p=1/40391, d=200000, n=1000000, k=4,9516, x=24,758, a=-0,0073337, A=1,03007. Portanto, a probabilidade de não haver seca é 1,03007*e -0,0073337*24,758 = 0,859042. Assim, a probabilidade de haver pelo menos uma seca é 1-0,859042 = 0,140958.
Segue a solução completa de 5 páginas de Gabor Megyesi (PDF). Obrigado, Gábor, pela sua ajuda.
Fiz uma simulação aleatória de 32.095 conjuntos de um milhão de mãos. O número de mãos com pelo menos uma sequência de três mãos (dry) foi 4.558, o que corresponde a uma probabilidade de 14,20%.
Imagine que você tenha duas mãos de pôquer de cinco cartas, distribuídas de baralhos diferentes. Você sabe que a mão A contém pelo menos um ás. Você sabe que a mão B contém o ás de espadas. Qual mão tem maior probabilidade de conter pelo menos mais um ás?
A tabela a seguir mostra a probabilidade de se obter de 0 a 4 ases em uma mão totalmente aleatória.
Probabilidades de Ás — Mão Aleatória
| Ases | Fórmula | Combinações | Probabilidade |
|---|---|---|---|
| 0 | combin(48,5) | 1712304 | 0,658842 |
| 1 | combin(4,1)×combin(48,4) | 778320 | 0,299474 |
| 2 | combin(4,2)×combin(48,3) | 103776 | 0,03993 |
| 3 | combin(4,3)×combin(48,2) | 4512 | 0,001736 |
| 4 | combin(4,4)×combin(48,1) | 48 | 0,000018 |
| Total | 2598960 | 1 |
Somando os valores de 1 a 4 ases, vemos que a probabilidade de haver pelo menos um ás é de 0,341158. A probabilidade de haver dois ou mais ases é de 0,041684.
A probabilidade de haver pelo menos mais um ás, dado que há pelo menos um, pode ser reformulada pelo teorema de Bayes como probabilidade(dois ou mais ases dado pelo menos um ás) = probabilidade(dois ou mais ases)/probabilidade(pelo menos um ás) = 0,041684/ 0,341158 = 0,122185.
Para quem não se lembra bem do Teorema de Bayes, ele afirma que a probabilidade de A dado B é igual à probabilidade de A e B dividida pela probabilidade de B, ou seja, Pr(A dado B) = Pr(A e B)/Pr(B).
A próxima tabela mostra as combinações e a probabilidade para cada número de outros ases, dado que o ás de espadas foi removido do baralho.
Probabilidades do Ás — Mão sem Ás
| Ases | Fórmula | Combinações | Probabilidade |
|---|---|---|---|
| 0 | combin(3,0)×combin(48,4) | 194580 | 0,778631 |
| 1 | combin(3,1)×combin(48,3) | 51888 | 0,207635 |
| 2 | combin(3,2)×combin(48,2) | 3384 | 0,013541 |
| 3 | combin(3,3)×combin(48,1) | 48 | 0,000192 |
| Total | 249900 | 1 |
Isso mostra que a probabilidade de haver pelo menos mais um ás é de 0,221369.
Para nos divertirmos, vamos resolver a mesma questão usando o Teorema de Bayes. Suponha que mãos aleatórias sejam distribuídas até que uma contenha o ás de espadas. A probabilidade de haver pelo menos um ás adicional, dado que a mão contém o ás de espadas, pode ser reescrita como probabilidade(pelo menos dois ases dado que há um ás de espadas na mão). De acordo com o Teorema de Bayes, isso é igual a Probabilidade(a mão contém o ás de espadas e pelo menos mais um ás) / Pr(a mão contém o ás de espadas). Podemos decompor o numerador como Probabilidade(2 ases incluindo o ás de espadas) + Probabilidade(3 ases incluindo o ás de espadas) + Probabilidade(4 ases). Usando a primeira tabela, isso é igual a 0,039930×(2/4) + 0,001736×(3/4) + 0,000018 = 0,021285. A probabilidade de sair o ás de espadas é 5/52 = 0,096154. Portanto, a probabilidade de sair pelo menos dois ases, dado o ás de espadas, é 0,021285/0,096154 = 0,221369.
Assim, a probabilidade de se obter dois ou mais ases, dado que pelo menos um ás já está na mesa, é de 12,22%, e dado que o ás de espadas é de 22,14%.
Certo, acredito nos seus números, mas ainda não faz sentido para mim. Eu imaginaria que as probabilidades seriam iguais. Que diferença o naipe faz para o ás que você tem?
Vamos analisar outra situação mais simples. Suponha que a mulher A diga: "Tenho dois filhos e pelo menos um é menino". A mulher B diz: "Tenho dois filhos e o mais velho se chama John". Podemos assumir que ninguém chamado John é menina e que nenhuma mulher dá o mesmo nome a mais de um filho. Usando a probabilidade condicional, a probabilidade de ambos os filhos da mulher A serem meninos é pr(ambos meninos)/pr(pelo menos um menino) = pr(ambos meninos)/(1-pr(ambas meninas)) = (1/4)/(1-(1/4)) = (1/4)/(3/4) = 1/3. No entanto, a probabilidade de o filho mais novo da mulher B ser menino, ou de ambos os filhos serem meninos, é desconhecida, porque dizer que o filho mais velho se chama John não nos diz nada sobre o filho mais novo.
Para dar outro exemplo, imagine que você vai à Jiffy Lube e eles oferecem duas promoções pelo mesmo preço. A promoção A consiste em verificar quatro peças e substituir apenas a primeira defeituosa encontrada. A promoção B consiste em verificar apenas um problema e consertá-lo, caso seja encontrado. Você não preferiria a promoção A? Seu carro chegou com o mesmo número de peças com defeito esperado, mas a probabilidade de encontrar um problema é maior na promoção A, e, portanto, você sairá com um número menor de peças com defeito esperado. Da mesma forma, um teste para qualquer ás provavelmente revelará o único ás, enquanto um teste para o ás de espadas não verifica os outros três naipes, tornando mais provável que sejam ases.
Como você chegou ao número de 2072 sequências de flush usando 4 cartas de um total de 5 no pôquer de quatro cartas?
Primeiro, separei os straight flushes em dois tipos: aqueles com quatro cartas consecutivas do mesmo naipe e aqueles com cinco. O número de straight flushes de cinco cartas é o número de naipes multiplicado pelo número de combinações possíveis (do ás ao 10 como carta mais baixa) = 4 * 10 = 40. Para os straight flushes de quatro cartas, existem 11 combinações diferentes (do ás ao valete como carta mais baixa). No caso dos straight flushes A234 e JQKA, a quinta carta pode ser uma de 47 (52 menos as 4 cartas já removidas e a quinta carta que formaria um straight flush de 5 cartas, que já foram contabilizadas). Portanto, existem 4 * 2 * 47 = 376 straight flushes com a combinação A234 ou JQKA. Das outras nove combinações possíveis, existem 46 cartas possíveis para a quinta carta (52 menos as 4 cartas já removidas e duas para cartas que formariam um straight flush de cinco cartas). Assim, o número de straight flushes com a combinação 2345 a TJQK é 4 * 9 * 46 = 1656. Portanto, o número total de sequências de quatro cartas (straight flush) é 40 + 376 + 1656 = 2072.
É 100% possível formar um flush com a 17ª carta, independentemente de qual seja. Quando é que uma sequência é 100% possível com qual número de cartas?
Uma sequência só é garantida com 45 cartas. Por exemplo, você poderia distribuir todas as cartas A, 2, 3, 4, 6, 7, 8, 9, JQ e K, totalizando 44 cartas, e ainda assim não conseguiria formar uma sequência.
Prezado e incrível Sr. Mago das Probabilidades, estou completamente impressionado com sua perspicácia estatística. Por acaso, o senhor poderia calcular para mim a probabilidade de uma sequência de sete cartas — ou seja, A, 2, 3, 4, 5, 6, 7 ou 2, 3, 4, 5, 6, 7, 8 ou 7, 8, 9, 10, valete, dama, rei — no pôquer de sete cartas? Reconhecemos que esta não é uma mão de pôquer real; no entanto, surgiu durante uma partida e ficamos curiosos para saber se a probabilidade é menor do que a de um full house normal no pôquer de sete cartas. Obrigado, ó sábio.
Como posso recusar depois de você ter me bajulado tanto? Primeiro, existem combin (52,7) = 133.784.560 maneiras de escolher 7 cartas dentre 52, sem levar em conta a ordem. Existem 8 combinações possíveis para uma sequência de 7 cartas (a carta mais baixa pode ser de Ás a 8). Se tivéssemos 7 valores diferentes, haveria 4⁷ = 16.384 maneiras de organizar os naipes. Observe que isso inclui todas as cartas do mesmo naipe, o que formaria uma sequência de flush. Portanto, a probabilidade é 8 * 16.384 / 133.784.560 = 1 em 1020,6952.
Se eu distribuir 4 cartas de um mesmo baralho, qual a probabilidade de pelo menos uma delas ser de espadas?
A probabilidade de zero espadas é (39/52)*(38/51)*(37/50)*(36/49) = 0,303818. Portanto, a probabilidade de pelo menos uma espada é 1-0,303818 = 0,696182.
Em um jogo com um único baralho, qual é a probabilidade de obter pelo menos um ás e um dois em quatro cartas? Essa informação é útil para o jogo de Omaha.
Pela probabilidade básica, sabemos que Pr(A ou B) = Pr(A) + Pr(B) - Pr(A e B). Portanto, Pr(A e B) = Pr(A) + Pr(B) - Pr(A ou B). Suponhamos que A tire um ás e B tire um dois. Pr(A) = Pr(pelo menos um ás) = 1 - Pr(nenhum ás) = 1 - combin(48,4) / combin (52,4) = 1 - 0,7187 = 0,2813. A probabilidade de não haver dois seria obviamente a mesma. Pela mesma lógica, Pr(A ou B) = Pr(pelo menos um ás ou dois) = 1 - Pr(nenhum ás nem dois) = 1 - combin(44,4) / combin(52,4) = 1 - 0,501435 = 0,498565. Assim, a probabilidade de obter pelo menos um ás e um dois é 0,2813 + 0,2813 - 0,498565 = 0,063962.
Qual a probabilidade de receber o valete de ouros 27 vezes seguidas em um jogo de seis cartas?
A probabilidade de obtê-la em qualquer mão é 6/52. A probabilidade de obtê-la em 27 mãos seguidas é (6/52) 27 = 1 em 20.989.713.842.161.800.000.000.000.
Qual é a probabilidade de obter a "mão do homem morto", um par de ases e oitos?
Existem seis maneiras de organizar dois naipes dentre os quatro para cada par. Além disso, há 44 cartas para a carta isolada. Portanto, o número de combinações bem-sucedidas é 6 * 6 * 44 = 1584. Há 2.598.960 combinações no total, então a probabilidade é de 0,0609%.
Entendo que você já respondeu que a probabilidade de obter a "mão do homem morto", um par de ases e oitos, é de 0,0609% em 3 de abril de 2005 , mas acredito que a mão do homem morto seja "dois ases pretos, dois oitos pretos e a dama de paus". Qual é a probabilidade de tirar exatamente essa mão de um baralho padrão?
Só existe uma maneira de obter essa mão exata. Portanto, a probabilidade seria 1 em combin(52,5) ou 1 em 2.598.960.
Quais são as chances/probabilidades de cada possível mão de cinco cartas que pode ser formada a partir de um baralho padrão de 52 cartas, onde o naipe de uma única carta não repetida na mão é considerado genérico? Por exemplo, considere a mão A♠ A♣ A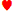 UM
UM 2. Nesta mão, o naipe do 2 é desconsiderado e representaria qualquer um dos quatro 2 do baralho. Outro exemplo é AJ-8-6-5. Nesta mão, o naipe de todas as 5 cartas é desconsiderado, de modo que apenas uma combinação desse tipo pode ocorrer. Outro exemplo: 3♠ 3
2. Nesta mão, o naipe do 2 é desconsiderado e representaria qualquer um dos quatro 2 do baralho. Outro exemplo é AJ-8-6-5. Nesta mão, o naipe de todas as 5 cartas é desconsiderado, de modo que apenas uma combinação desse tipo pode ocorrer. Outro exemplo: 3♠ 3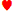 7♣ 7♠ Q. Nesta mão, o naipe dos dois 3 e dos dois 4 não é desconsiderado por haver mais de um na mão, mas o naipe da Q é genérico. Em outras palavras, o naipe de qualquer carta que não seja duplicada em uma mão é desconsiderado e essa mão é considerada uma das mãos possíveis, mesmo que houvesse muitas possibilidades de a mão se repetir se o naipe de cada carta não fosse desconsiderado. Assim, uma sequência ou flush composto por cinco cartas específicas, digamos Q.
7♣ 7♠ Q. Nesta mão, o naipe dos dois 3 e dos dois 4 não é desconsiderado por haver mais de um na mão, mas o naipe da Q é genérico. Em outras palavras, o naipe de qualquer carta que não seja duplicada em uma mão é desconsiderado e essa mão é considerada uma das mãos possíveis, mesmo que houvesse muitas possibilidades de a mão se repetir se o naipe de cada carta não fosse desconsiderado. Assim, uma sequência ou flush composto por cinco cartas específicas, digamos Q.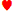 J♣ 10
J♣ 10 9
9 8♠ ou A♠ J♠ 8♠ 7♠ 3♠ só podem ocorrer uma vez, pois qualquer outra combinação dessas mesmas cartas, mesmo que em um naipe diferente, seria uma duplicata. Portanto, usando esse critério, qual é a probabilidade de ocorrência de uma única mão? Em outras palavras, quantas mãos de cinco cartas como essa existem em um baralho padrão de 52 cartas? Agradeço sua ajuda.
8♠ ou A♠ J♠ 8♠ 7♠ 3♠ só podem ocorrer uma vez, pois qualquer outra combinação dessas mesmas cartas, mesmo que em um naipe diferente, seria uma duplicata. Portanto, usando esse critério, qual é a probabilidade de ocorrência de uma única mão? Em outras palavras, quantas mãos de cinco cartas como essa existem em um baralho padrão de 52 cartas? Agradeço sua ajuda.
Estou muito familiarizado com esse conceito. Existem 134.459 mãos únicas de cinco cartas. Sei disso porque meu primeiro programa de vídeo pôquer analisou todas as 2.598.960 mãos possíveis e levou dias para percorrer toda a tabela de pagamentos. No entanto, ao executar apenas uma simulação de cada uma das 134.459 classes de mãos, ponderando pelo número total de mãos em sua classe, é possível reduzir o tempo de execução em 95%. Às vezes, quando um jogo é específico para um naipe, como minha análise recente do Blackjack Bonus Poker , preciso desempoeirar meu programa antigo e fazer a análise da maneira mais lenta.
Quais são as probabilidades no jogo de cinco cartas usando um baralho com 5 naipes em vez de 4?
Combinações no pôquer de cinco naipes
| Mão | Combinações | Probabilidade | Fórmula |
| Cinco de um tipo | 13 | 0,000002 | 13 |
| Straight flush | 50 | 0,000006 | 5*10 |
| Quatro de um mesmo tipo | 3900 | 0,000472 | 13*12* COMBINAR (5,4)*5 |
| Descarga | 6385 | 0,000773 | 5*(COMBIN(13,5)-10) |
| Casa cheia | 15600 | 0,001889 | 13*12*COMBIN(5,3)*COMBIN(5,2) |
| Direto | 31200 | 0,003777 | 10*(5^5-5) |
| Três de um tipo | 214500 | 0,025969 | 13*COMBIN(12,2)*COMBIN(5,3)*5^2 |
| Dois pares | 429000 | 0,051938 | COMBIN(13,2)*11*COMBIN(5,2)^2*5 |
| Par | 3575000 | 0,432815 | 13*COMBIN(12,3)*COMBIN(5,3)*5^3 |
| Nada | 3984240 | 0,48236 | (COMBIN(13,5)-10)*(5^5-5) |
| Total | 8259888 | 1 |
Observe que inverti a ordem do enchimento da casa e da descarga.
Quantas combinações de cinco cartas de um baralho padrão possuem cartas de exatamente dois naipes?
Os dois naipes podem ser divididos em 4 e 1 ou 3 e 2. Vamos analisar primeiro a divisão 4/1. Há 4 naipes para escolher para o naipe com 4 cartas e 3 restantes para o naipe com 1 carta. Existem combin(13,4) = 715 maneiras de escolher 4 valores entre 13. Existem 13 maneiras de escolher um único valor. Portanto, existem 4 × 3 × 715 × 13 = 111.540 maneiras de ter uma divisão 4/1 entre os dois naipes. Por lógica semelhante, existem 4 × 3 × combin(13,3) × combin(13,2) = 267.696 maneiras de ter uma divisão 3/2. Assim, a probabilidade geral é (111.540 + 267.696) / combin(52,5) = 14,59%.
Qual a probabilidade de receber 2-3-4-5-7 de naipes diferentes? Muito obrigado, o site é ótimo!
Obrigado. (4 5 -4)/combin(52,5) = 1020/2598960 = 1 em 2.548.
Estava no Foxwoods outro dia, assistindo às duas mesas finais do Foxwoods Poker Classic. Quando Vince Van Patten (um dos apresentadores do World Poker Tour) chegou para assistir, começou a fazer todos os tipos de apostas paralelas com alguns dos jogadores profissionais de pôquer que estavam por perto. Ele estava oferecendo 20 para 1 para quem conseguisse virar um baralho inteiro de cartas, percorrendo os valores e dizendo em voz alta, enquanto tirava cada carta: Ás, 2, 3, 4, e assim por diante até o Rei, recomeçando no Ás, sem que a carta anunciada aparecesse. Ninguém conseguiu chegar ao final e Vince ganhou algumas centenas de dólares em cerca de 10 minutos antes de todos desistirem. Sei que isso deve ser possível, mas tenho a impressão de que Vince está se esforçando bastante para conseguir fazer isso, oferecendo apenas 20 para 1. Quais são as chances de realmente conseguir virar o baralho inteiro?
Uma maneira simples de estimar a probabilidade de ganhar é assumir que cada carta tem uma probabilidade de 12/13 de não corresponder ao valor declarado. Para ganhar essa aposta, a vítima teria que fazer isso com sucesso 52 vezes. A probabilidade de 52 vitórias é (12/13) × 52 = 1,56%. Um preço justo a pagar seria 63,2 para 1. Com 20 para 1, Vince tinha uma vantagem de 67,3% (ai!).
Segundo o GM, que é um matemático melhor do que eu, a probabilidade real é de 1,6232727%. A razão para a diferença é que o resultado de cada escolha está positivamente correlacionado com as escolhas anteriores.
Jogando ontem à noite, um dos jogadores, um velho astuto, desleixado e agressivo, desafiou a mesa para fazer apostas paralelas de odds iguais no flop. Esse velho rabugento apostava que uma das três cartas no flop seria um ás, um dois ou um valete (às vezes ele mudava as três cartas identificáveis). Quais são as probabilidades dessa aposta? Sua sábia opinião seria muito apreciada.
Antes de qualquer carta ser vista, a probabilidade de quaisquer três valores não aparecerem no flop é combin (40,3)/combin(52,3) = 9880/22100 = 44,71%. Portanto, esse cara tinha uma vantagem de 10,59%.
Suponha que cinco cartas sejam distribuídas de um baralho de 52 cartas e a primeira seja um rei. Qual é a probabilidade de haver pelo menos mais um rei? Eu vi um problema com o Ás que você estava resolvendo parecido com este, mas não consegui entender muito bem. Agradeço qualquer ajuda.
A maneira que prefiro para responder a questões de probabilidade é usando a função combinatória. Fazendo isso, existem combin (48,4) = 194.580 maneiras de escolher quatro cartas que não sejam reis dentre as 48 cartas que não são reis no baralho. Existem combin(51,4) = 249.900 maneiras de escolher quaisquer quatro cartas dentre as 51 cartas restantes no baralho. Portanto, a probabilidade de não obter nenhum rei nas próximas quatro cartas é 194.580/249.900 = 77,86%. Assim, a probabilidade de obter pelo menos um rei é 100% - 77,86% = 22,14%.
Várias pessoas disseram que a função combinatória provavelmente está além da compreensão do tipo de pessoa que faz esse tipo de pergunta simples de probabilidade. Eu concordo, mas um dos principais objetivos deste site é tentar ensinar matemática aos meus leitores. A função combinatória é extremamente útil em probabilidade e economiza muito tempo. No entanto, a questão em pauta pode ser facilmente respondida sem ela.
A probabilidade de a segunda carta não ser um rei é de 48/51. Isso ocorre porque restam 48 cartas que não são reis no baralho e 51 cartas no total. Se a segunda carta não for um rei, a probabilidade de a terceira carta também não ser um rei é de 47/50 (47 cartas que não são reis divididas por 50 cartas restantes). Seguindo essa lógica, a probabilidade de nenhuma das outras quatro cartas ser um rei é (48/51) × (47/50) × (46/49) × (45/48) = 77,86%. A probabilidade de que esse não seja o caso, ou seja, que haja pelo menos um rei, é de 100% - 77,86% = 22,14%.
Primeiro, escolha 5 cartas de um baralho de 52 cartas. Segundo, some os valores delas no blackjack (T, J, Q, K = 10, A = 1). Qual a probabilidade de a soma ser par/ímpar? Eu diria que, com a abundância de cartas pares, a probabilidade de a soma ser par é muito maior.
Surpreendentemente, um total ímpar é mais provável, com 50,03%, apesar de 30 das 52 cartas serem pares. A tabela a seguir mostra a probabilidade de cada divisão par/ímpar.
Pergunta ímpar/par
| pares | Chances | Combinações | Probabilidade | Soma |
| 0 | 5 | 15504 | 0,005965 | Chance |
| 1 | 4 | 155040 | 0,059655 | Até |
| 2 | 3 | 565440 | 0,217564 | Chance |
| 3 | 2 | 942400 | 0,362607 | Até |
| 4 | 1 | 719200 | 0,276726 | Chance |
| 5 | 0 | 201376 | 0,077483 | Até |
| Total | 2598960 | 1 |
Qual a probabilidade de, ao retirar três cartas de um baralho, uma delas ser exatamente um naipe de espadas?
A probabilidade de a primeira carta ser um naipe de espadas e as duas seguintes não serem é (13/52)×(39/51)×(38/50) = 14,53%. Multiplique esse valor por 3, pois o naipe de espadas pode ser qualquer uma das três cartas. Portanto, a resposta é 3×14,53% = 43,59%. Para quem prefere a função combinatória, a resposta é 13×combin(39,2)/ combin (52,3) = 9.633/22.100 = 43,59%.
Selecione dois números aleatórios entre 0 e 1 (com distribuição uniforme). Agora, selecione o menor dos dois. Qual é a média dos números selecionados? E no caso geral de n números?
Para dois números, a resposta é 1/3, e para n números é 1/(n+1). Publiquei as soluções na minha página de problemas de matemática , questões 194 e 195.
Você está jogando um jogo com três pessoas: (a) você, (b) seu oponente e (c) um árbitro. Cada um de vocês escolhe um número real entre 0 e 1 em segredo. Depois que todos os números forem escolhidos, eles são revelados. O jogador que acertar o número mais próximo do número do árbitro, sem ultrapassá-lo, ganha. Se você acertar o número mais próximo, ganha $1. Se o seu oponente acertar o número mais próximo, você perde $1. Se ambos os jogadores ultrapassarem o número escolhido, ou se houver um empate, o jogo termina empatado.
Existe algum número que você possa escolher que maximize seu retorno esperado, caso o outro jogador escolha aleatoriamente? E se o outro jogador também tiver uma estratégia?
Espero que esteja feliz, pois passei o dia inteiro na segunda parte e minha resposta ainda estava errada. Para não privar meus leitores da mesma alegria, não vou simplesmente divulgar as respostas aqui. Dividi o problema em duas partes e publiquei as respostas e soluções em mathproblems.info , problemas 196 e 197.
Se você escolher cinco cartas aleatoriamente de um baralho padrão de 52 cartas, qual é a probabilidade de que todos os quatro naipes estejam representados?
Teria que haver um naipe com duas cartas e três com uma carta cada. Existem quatro naipes possíveis para o naipe que aparece duas vezes. Para o naipe que aparece duas vezes, existem combinações (13,2) = 78 maneiras de escolher 2 valores entre os 13. Para cada um dos outros três naipes, existem 13 valores possíveis. Portanto, o número total de combinações é 4 × 78 × 13 × 13 × 13 = 685.464. Existem combinações (52,5) = 2.598.960 maneiras de escolher 5 cartas entre 52. Portanto, a probabilidade é 685.464/2.598.960 = 26,37%.
Qual a probabilidade de dois valores quaisquer escolhidos, por exemplo, dama e rei, aparecerem consecutivamente em um baralho aleatório? Alguém me desafiou para uma aposta de 1 para 1 de que isso aconteceria.
Segundo uma simulação aleatória, a probabilidade é de 48,64%. Portanto, eu teria aceitado essa aposta.
Você pode recomendar uma função para mapear quaisquer cinco cartas de um baralho de 52 cartas para um número inteiro de 0 a 2.598.959?
Sim. Primeiro, atribua a cada carta um valor de 0 a 51. Nomeie as cartas de c1 a c5, ordenando-as de c1 (a menor) a c5 (a maior). Em seguida, chame a seguinte função:
int GetIndex(int c1, int c2, int c3, int c4, int c5)
{
retornar combin(c5,5) + combin(c4,4)+ combin(c3,3) + combin(c2,2) + combin(c1,1);
}
Onde `combin` retorna o valor tradicional, exceto se o primeiro valor for menor que o segundo, caso em que retorna 0, da seguinte forma:
int combin(int x, int y)
{
se (y>x)
retornar 0;
outro
{
int i,n;
n=1;
para (i=x-y+1; i<=x; i++)
n*=i;
para (i=2; i<=y; i++)
n/=i;
retornar n;
}
}
Se você estiver fazendo isso para acessar um elemento de um array, carregue o array da seguinte forma.
contagem=0;
para (c5 = 4; c5 < 52; c5++)
{
para (c4 = 3; c4 < c5; c4++)
{
para (c3 = 2; c3 < c4; c3++)
{
para (c2 = 1; c2 < c3; c2++)
{
para (c1 = 0; c1 < c2; c1++)
{
index_array[count]=OQueVocêDeseja;
contar++;
}
}
}
}
}
Qual é a probabilidade de tirar 3 sequências de flush em 10 tentativas, tendo três cartas para formar uma sequência de flush com uma lacuna?

Este é um problema do tipo distribuição binomial. A fórmula geral é que se a probabilidade de um evento é p, e cada resultado é independente, então a probabilidade de ele acontecer exatamente w em t tentativas é combin (t,w)×p w ×(1-p) tw .
Neste caso, existem 2 maneiras de formar um straight flush. Você precisa do 8 de ouros e de outra carta, que pode ser o 6 ou o J de ouros. Existem combin(47,2) = 1.081 maneiras de tirar 2 cartas das 47 restantes no baralho. Portanto, a probabilidade de obter um straight flush em qualquer mão é 2/1.081 = 0,0018501. A probabilidade de formar 3 cartas de 10 é combin(10,3) × 0,0018501 = 3 × (1 - 0,0018501) = 7 = 0,000000750178, ou 1 em 1.333.017.
Dois baralhos de 54 cartas (incluindo dois curingas) são embaralhados. Um jogador recebe metade deles. Qual é a probabilidade de o jogador ter recebido todas as quatro cartas vermelhas do tipo três?
Existem 4 cartas vermelhas de valor 3 e 104 outras cartas. Há apenas uma maneira de obter todas as quatro cartas vermelhas de valor 3. Existem combin (104,50) = 1,46691 × 10²⁸ maneiras pelas quais o jogador poderia obter 50 das outras 104 cartas. O número total de combinações é combin(108,54) = 2,48578 × 10³⁰ . combin(104,50)/combin(108,54) = 0,059012.
Se você não gosta de lidar com números tão grandes, aqui está uma solução alternativa. Numere os quatro três vermelhos de 1 a 4. A probabilidade de o primeiro três vermelho estar na pilha do jogador é 54/108. Agora, remova o primeiro três. A probabilidade de o jogador ter o segundo três vermelho é 53/107, porque o jogador tem 53 cartas restantes e há 107 cartas restantes. Da mesma forma, a probabilidade de o jogador ter o terceiro três vermelho é 52/106 e a do quarto três vermelho é 51/105. (54/108) × (53/107) × (52/106) × (51/105) = 0,059012.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Em sua coluna de 14 de dezembro de 2010, você escreveu que a mão AAAAAKK, que é especificamente mencionada na descrição das regras da casa, pode nunca ter ocorrido na história do jogo. De acordo com outro crupiê, um jogador recebeu essa mão no Main Street Station em novembro de 2010.
Interessante. Como escrevi, estimo que essa mão ocorra aproximadamente uma vez a cada 23,7 anos em qualquer lugar de Nevada. Diria que essa foi uma dessas vezes.
Suponha que você escolha duas figuras, por exemplo, reis e rainhas. Qual é a probabilidade de que, pelo menos uma vez em um baralho de 52 cartas embaralhado aleatoriamente, um rei e uma rainha estejam lado a lado?
Eu cheguei a 48,6279%. Se você quiser apostar nisso, as probabilidades justas para o "sim" seriam de 1,0564 para 1.
Ouvi dizer que houve uma partida de bridge "perfeita" recentemente, onde cada jogador recebeu 13 cartas de um dos quatro naipes. Qual a probabilidade disso acontecer?
Há também rumores de que isso aconteceu em um jogo de whist em Warwickshire em 2011. Para benefício de outros leitores, a pergunta é qual a probabilidade de dividir um baralho de 52 cartas em quatro grupos de 13 cartas cada, onde cada conjunto é composto inteiramente pelas 13 cartas de um dos naipes.
Existem combin(52,13)*combin(39,13)*combin(26,13) = 53.644.737.765.488.800.000.000.000.000 maneiras possíveis de organizar 52 cartas em quatro conjuntos de 13 cartas. 4! = 2⁴ seria o número de combinações vencedoras, já que você poderia distribuir os quatro naipes aos quatro jogadores da maneira que quisesse. Portanto, a probabilidade é igual a 1 em 2.235.197.406.895.370.000.000.000.000. Para dar uma perspectiva a esse número, se todas as 7,5 bilhões de pessoas na Terra distribuíssem mãos de bridge a uma taxa de uma por segundo, a probabilidade de alguém distribuir uma mão considerada perfeita antes da explosão do Sol daqui a 5 bilhões de anos seria de 1 em 16.558.
No entanto, alguns definem uma mão "perfeita" como aquela em que um jogador recebe todas as 13 cartas de qualquer naipe. Demonstro que a probabilidade disso acontecer é de 1 em 39.688.347.497 partidas. Provavelmente, isso acontece de vez em quando em algum lugar do mundo.
Qual é a probabilidade, no Texas Hold'em, de dois jogadores terem um flush na mesma mão, usando ambas as cartas da mão?
Primeiro, vamos determinar o número de combinações de cartas do jogador e do tabuleiro em que isso pode acontecer. Obviamente, existem quatro naipes. Então, existem combin(13,4)=715 maneiras de escolher quatro das 13 cartas do naipe dado.
Em segundo lugar, uma maneira de isso acontecer é com três cartas do mesmo naipe que os jogadores têm no tabuleiro e as outras duas entre as 39 cartas restantes. Há combin(9,3)=84 maneiras de o tabuleiro ter três das 9 cartas restantes do naipe escolhido. Então, há combin(39,2)=741 maneiras de escolher mais duas cartas dentre as 39 restantes dos outros três naipes. Portanto, há 84*741=62.244 maneiras de ter três cartas do naipe em questão no tabuleiro.
Terceiro, outra maneira pela qual isso poderia acontecer é com quatro cartas do mesmo naipe que os jogadores têm na mesa e a outra carta entre as 39 restantes. Existem combin(9,4) = 126 maneiras de a mesa ter quatro das 9 cartas restantes do naipe escolhido. Então, existem 39 maneiras de escolher mais uma carta dentre as 39 restantes dos outros três naipes. No entanto, nem todas essas combinações resultarão em ambos os jogadores usando as duas cartas fechadas. Para que essa condição seja satisfeita, a carta de menor valor do naipe em questão deve estar na mesa. A probabilidade disso, dentre as 8 cartas desse naipe em jogo, é 4/8 = 1/2. Portanto, existem 126 * 39 * (1/2) = 2.457 maneiras de haver quatro cartas do naipe em questão na mesa.
Em quarto lugar, a última maneira pela qual isso poderia acontecer é com cinco cartas do mesmo naipe que os jogadores têm na mesa. Existem combin(9,5) = 126 maneiras de a mesa ter cinco das 9 cartas restantes do naipe escolhido. No entanto, nem todas essas situações resultarão em ambos os jogadores usando suas duas cartas fechadas. Para que essa condição seja atendida, as duas cartas de menor valor do naipe em questão devem estar na mesa. A probabilidade disso, dentre as 9 cartas desse naipe em jogo, é combin(5,2)/combin(9,2) = 10/36 = 5/18. Portanto, existem 126 * (5/18) = 35 maneiras de haver quatro cartas do naipe em questão na mesa.
Portanto, o número de combinações onde isso acontecerá é 715*(62.244 + 2.457 + 35) = 46.286.240.
O número total de combinações de maneiras de escolher quatro cartas para as cartas fechadas do jogador de 52 e mais 5 das 48 restantes no tabuleiro é combin(52,4)*combin(48,5) = 463.563.500.400.
Assim, a probabilidade é 46.286.240 / 463.563.500.400 = 0,000399395 = 1 em 2.504.
Essa pergunta foi feita e discutida no meu fórum no Wizard of Vegas .
Uma crupiê está trabalhando em uma nova variante do Three Card Poker. Ela pega todas as cartas com figuras de um baralho padrão e as embaralha completamente. Em seguida, distribui 3 cartas para o Jogador 1, 3 cartas para o Jogador 2, 3 cartas para o Jogador 3 e as 3 cartas finais para o Jogador 4. Qual é a probabilidade de que todas as quatro mãos contenham uma sequência (JQK de qualquer naipe)?
Distribua as cartas para um jogador de cada vez. A probabilidade de o primeiro jogador receber uma carta de cada valor é 4^3/combin(12,3) = 64/220.
Supondo que o primeiro jogador tenha conseguido uma sequência, restará um baralho reduzido com três cartas de cada valor. A probabilidade de o segundo jogador conseguir uma carta de cada valor é 3^3/combin(9,3) = 27/84.
Supondo que os dois primeiros jogadores tenham conseguido uma sequência, restará um baralho reduzido com duas cartas de cada valor. A probabilidade de o terceiro jogador conseguir uma carta de cada valor é 2^3/combin(6,3) = 8/20.
Supondo que os três primeiros jogadores tenham conseguido uma sequência, restará um baralho reduzido com uma carta de cada valor. Essas três cartas obviamente formam uma sequência.
Assim, a probabilidade de todos os quatro jogadores conseguirem uma sequência é (64/220)*(27/84)*(8/20)*1 = 216/5775 = 72/1925 = 3,74%.
Essa pergunta é feita e discutida no meu fórum no Wizard of Vegas, começando com esta postagem .
Suponha que eu tenha um baralho de 48 cartas, dividido em quatro naipes, com doze cartas de cada naipe. Se eu comprar 15 cartas, qual é a probabilidade de eu comprar pelo menos uma carta de cada naipe?
Vamos começar com 100% e subtrair as probabilidades que resultam em menos de quatro naipes.
Qual é a probabilidade de que as 48 cartas não tenham nenhuma carta de copas, por exemplo? Existem 36 cartas que não são de copas. O número de maneiras de escolher 15 cartas dentre as 36 é combin(36,15) = 5.567.902.560. O número de maneiras de escolher 15 cartas dentre todas as 48 é 1.093.260.079.344. Portanto, a probabilidade de que as 15 cartas não tenham nenhuma carta de copas é 5.567.902.560 / 1.093.260.079.344 = 0,005093.
Em seguida, vamos multiplicar isso por quatro, para obter a probabilidade de não ter nenhum naipe, não apenas copas: 4 × combin(36,15)/combin(48,15) = 0,02037174.
No entanto, isso contabiliza duas vezes algumas situações. Considere receber 15 cartas pretas. Isso omitiria copas e ouros. Teríamos contabilizado essa situação duas vezes. Portanto, precisamos corrigir isso. Existem combin(4,2) = 6 maneiras de escolher dois naipes dentre quatro. A probabilidade de todas as 15 cartas serem de dois naipes específicos quaisquer é combin(24,15)/combin(48,15) = 1.307.504/1.093.260.079.344 = 0,00000120. Como mencionado, existem seis maneiras de escolher dois naipes dentre quatro, então o número de maneiras pelas quais todas as cartas serão de dois naipes é 6 × combin(24,15)/combin(48,15) = 0,00000718.
Subtraindo o que contamos duas vezes, obtemos uma probabilidade de dois ou três naipes serem representados de 0,02037174 - 0,00000718 = 0,02036456.
Note que não precisamos nos preocupar com a representação de um único naipe, pois é impossível escolher 15 cartas dentre 12.
Como etapa final, subtraia a probabilidade de 2 ou 3 naipes de 100% para obter a probabilidade de todos os quatro naipes estarem representados: 1,00000000 - 0,02037174 = 0,97963544.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Se eu distribuísse 13 cartas de um baralho embaralhado (presumivelmente aleatório), quantas classificações diferentes eu esperaria ver?
Este é um problema típico de Cadeia de Markov, se é que já houve algum.
A tabela a seguir mostra o número esperado de posições (de 0 a 4 cartas) para todos os números de cartas distribuídas, de 1 a 52.
Classificações esperadas pelas cartas distribuídas
| Cartões | 0 posições | 1º lugar | 2 patentes | 3 níveis | 4 níveis | Esperado Classificações |
|---|---|---|---|---|---|---|
| 1 | 12.000000 | 1.000000 | 0,000000 | 0,000000 | 0,000000 | 1.000000 |
| 2 | 11.058824 | 1,882353 | 0,058824 | 0,000000 | 0,000000 | 1,941176 |
| 3 | 10,174118 | 2,654118 | 0,169412 | 0,002353 | 0,000000 | 2,825882 |
| 4 | 9,343577 | 3,322161 | 0,324994 | 0,009220 | 0,000048 | 3,656423 |
| 5 | 8,564946 | 3,893157 | 0,519088 | 0,022569 | 0,000240 | 4,435054 |
| 6 | 7,836014 | 4,373589 | 0,745498 | 0,044178 | 0,000720 | 5,163986 |
| 7 | 7,154622 | 4,769748 | 0,998319 | 0,075630 | 0,001681 | 5,845378 |
| 8 | 6,518655 | 5,087731 | 1,271933 | 0,118319 | 0,003361 | 6,481345 |
| 9 | 5,926050 | 5,333445 | 1,561008 | 0,173445 | 0,006050 | 7,073950 |
| 10 | 5,374790 | 5,512605 | 1,860504 | 0,242017 | 0,010084 | 7,625210 |
| 11 | 4,862905 | 5,630732 | 2,165666 | 0,324850 | 0,015846 | 8,137095 |
| 12 | 4,388475 | 5,693157 | 2,472029 | 0,422569 | 0,023770 | 8,611525 |
| 13 | 3,949628 | 5.705018 | 2,775414 | 0,535606 | 0,034334 | 9.050372 |
| 14 | 3,544538 | 5,671261 | 3,071933 | 0,664202 | 0,048067 | 9,455462 |
| 15 | 3,171429 | 5,596639 | 3,357983 | 0,808403 | 0,065546 | 9,828571 |
| 16 | 2,828571 | 5,485714 | 3,630252 | 0,968067 | 0,087395 | 10,171429 |
| 17 | 2,514286 | 5,342857 | 3,885714 | 1,142857 | 0,114286 | 10,485714 |
| 18 | 2,226939 | 5,172245 | 4,121633 | 1,332245 | 0,146939 | 10,773061 |
| 19 | 1,964946 | 4,977863 | 4,335558 | 1,535510 | 0,186122 | 11.035054 |
| 20 | 1,726771 | 4,763505 | 4,525330 | 1,751741 | 0,232653 | 11,273229 |
| 21 | 1,510924 | 4,532773 | 4,689076 | 1,979832 | 0,287395 | 11,489076 |
| 22 | 1,315966 | 4,289076 | 4,825210 | 2,218487 | 0,351261 | 11,684034 |
| 23 | 1.140504 | 4,035630 | 4,932437 | 2,466218 | 0,425210 | 11,859496 |
| 24 | 0,983193 | 3,775462 | 5,009748 | 2,721345 | 0,510252 | 12.016807 |
| 25 | 0,842737 | 3,511405 | 5,056423 | 2,981993 | 0,607443 | 12.157263 |
| 26 | 0,717887 | 3,246098 | 5.072029 | 3,246098 | 0,717887 | 12.282113 |
| 27 | 0,607443 | 2,981993 | 5,056423 | 3,511405 | 0,842737 | 12,392557 |
| 28 | 0,510252 | 2,721345 | 5,009748 | 3,775462 | 0,983193 | 12,489748 |
| 29 | 0,425210 | 2,466218 | 4,932437 | 4,035630 | 1.140504 | 12.574790 |
| 30 | 0,351261 | 2,218487 | 4,825210 | 4,289076 | 1,315966 | 12,648739 |
| 31 | 0,287395 | 1,979832 | 4,689076 | 4,532773 | 1,510924 | 12,712605 |
| 32 | 0,232653 | 1,751741 | 4,525330 | 4,763505 | 1,726771 | 12,767347 |
| 33 | 0,186122 | 1,535510 | 4,335558 | 4,977863 | 1,964946 | 12,813878 |
| 34 | 0,146939 | 1,332245 | 4,121633 | 5,172245 | 2,226939 | 12,853061 |
| 35 | 0,114286 | 1,142857 | 3,885714 | 5,342857 | 2,514286 | 12,885714 |
| 36 | 0,087395 | 0,968067 | 3,630252 | 5,485714 | 2,828571 | 12.912605 |
| 37 | 0,065546 | 0,808403 | 3,357983 | 5,596639 | 3,171429 | 12,934454 |
| 38 | 0,048067 | 0,664202 | 3,071933 | 5,671261 | 3,544538 | 12,951933 |
| 39 | 0,034334 | 0,535606 | 2,775414 | 5.705018 | 3,949628 | 12,965666 |
| 40 | 0,023770 | 0,422569 | 2,472029 | 5,693157 | 4,388475 | 12,976230 |
| 41 | 0,015846 | 0,324850 | 2,165666 | 5,630732 | 4,862905 | 12,984154 |
| 42 | 0,010084 | 0,242017 | 1,860504 | 5,512605 | 5,374790 | 12,989916 |
| 43 | 0,006050 | 0,173445 | 1,561008 | 5,333445 | 5,926050 | 12,993950 |
| 44 | 0,003361 | 0,118319 | 1,271933 | 5,087731 | 6,518655 | 12,996639 |
| 45 | 0,001681 | 0,075630 | 0,998319 | 4,769748 | 7,154622 | 12,998319 |
| 46 | 0,000720 | 0,044178 | 0,745498 | 4,373589 | 7,836014 | 12,999280 |
| 47 | 0,000240 | 0,022569 | 0,519088 | 3,893157 | 8,564946 | 12,999760 |
| 48 | 0,000048 | 0,009220 | 0,324994 | 3,322161 | 9,343577 | 12,999952 |
| 49 | 0,000000 | 0,002353 | 0,169412 | 2,654118 | 10,174118 | 13.000000 |
| 50 | 0,000000 | 0,000000 | 0,058824 | 1,882353 | 11.058824 | 13.000000 |
| 51 | 0,000000 | 0,000000 | 0,000000 | 1.000000 | 12.000000 | 13.000000 |
| 52 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 13.000000 | 13.000000 |
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Alguém me desafiou para a seguinte aposta. Eu posso escolher três cartas de um baralho de pôquer padrão, anotando meu palpite, mas mantendo-o em segredo até o final. Por exemplo, 7-Ás-2. Ele então me ofereceu uma aposta de valor igual que conseguiria acertar pelo menos uma das minhas cartas se recebesse três palpites. Quais eram as minhas chances de ganhar?
Para ganhar, seu oponente precisa errar todas as três previsões. A primeira previsão tem 10/13 de chance de estar errada. A segunda previsão tem 9/12 de chance de estar errada, porque podemos descartar a primeira classificação como possibilidade. A terceira previsão tem 8/11 de chance de estar errada, porque podemos descartar as duas primeiras classificações como possibilidade.
Todas as três coisas teriam que acontecer para você ganhar. Assim, as chances de você ganhar são (10/13) * (9/12) * (8/11) = 720/1716 = 41,96%.
Com odds de 1 para 1, a vantagem da casa nessa aposta, do seu lado, é de 16,08% (ai!).
Esta pergunta foi extraída do livro The Book of Proposition Bets, de Owen E'Shea (número 7).
Alguém me desafiou para uma aposta: ele conseguiria tirar um total de 12 com dois dados em 27 lançamentos. Se não conseguisse, eu ganharia o dobro do valor apostado. Como a probabilidade de tirar 12 é de 1/36, não deveria ele precisar de 36 lançamentos em média para conseguir um 12? Parece que as probabilidades estariam a meu favor se meu oponente fizesse apenas 27 lançamentos. Estou certo ou onde está o erro nos meus cálculos?
O tempo médio de espera entre um 12 e outro é de 36 lançamentos, incluindo o próprio lançamento do 12. No entanto, isso não significa que eles aparecem exatamente a cada 36 lançamentos. A probabilidade de NÃO tirar um 12 é (35/36). A probabilidade de não tirar um 12 em 27 lançamentos é (35/36)^27. Portanto, a probabilidade de tirar pelo menos um 12 é 1 - (35/36)^27 = 53,26%.
A tabela a seguir mostra a probabilidade de obter pelo menos 12 em 20 a 36 lançamentos. Observe que são necessários 25 lançamentos para ter vantagem com probabilidades iguais.
Probabilidade 12
| Rolls | Probabilidade |
|---|---|
| 20 | 43,07% |
| 21 | 44,66% |
| 22 | 46,19% |
| 23 | 47,69% |
| 24 | 49,14% |
| 25 | 50,55% |
| 26 | 51,93% |
| 27 | 53,26% |
| 28 | 54,56% |
| 29 | 55,82% |
| 30 | 57,05% |
| 31 | 58,24% |
| 32 | 59,40% |
| 33 | 60,53% |
| 34 | 61,63% |
| 35 | 62,69% |
| 36 | 63,73% |
Sabemos que existem combin(52,5) = 2.598.960 combinações possíveis de cinco cartas dentre 52. Minha pergunta é: quantas mãos de cinco cartas são possíveis com um sapato de cinco baralhos?
Vamos analisar um tipo de mão de cada vez.
- Cinco cartas iguais: Um baralho contém 52 cartas diferentes, resultando em 52 combinações.
- Quatro cartas iguais: Existem 52 combinações possíveis de quatro cartas iguais e 51 combinações possíveis de uma carta única. Portanto, existem 52 * 51 = 2.652 combinações possíveis para uma quadra.
- Três cartas iguais e duas cartas diferentes: Existem 52 combinações possíveis para as três cartas iguais e 51 para o par. Portanto, existem 52 * 51 = 2.652 combinações possíveis para um full house.
- Três cartas iguais e duas cartas diferentes: Existem 52 combinações possíveis para as três cartas iguais e combin(51,2)=1.275 para as duas cartas diferentes. Portanto, existem 52 * 1.275 = 66.300 combinações possíveis para uma trinca.
- Dois pares de cartas iguais e uma carta avulsa: Existem combin(52,2) = 1.326 combinações para as duas cartas diferentes que formam pares. Restam então 50 combinações para a carta avulsa. Portanto, existem 1.326 * 50 = 66.300 combinações possíveis para um par de duas cartas.
- Um par de cartas iguais e três cartas avulsas: Existem 52 cartas possíveis para o par. Então, existem combin(51,3) = 20.825 maneiras de escolher 3 cartas dentre as 51 restantes para as cartas avulsas. Portanto, o número de combinações para um par é 52 * 20.825 = 1.082.900.
- Cinco singletons: Existem combin(52,5)=2.598.960 maneiras de escolher cinco cartas dentre 52.
A soma de todas essas combinações é 3.819.816.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .


