Probabilidade - Moedas
Se uma moeda for lançada 1000 vezes, qual é a probabilidade de o número total de caras estar no intervalo de 452 a 548?
Para este problema, podemos usar a aproximação normal da distribuição binomial. A variância do número de caras é 1000*(1/2)*(1/2) = 250. Portanto, o desvio padrão é 250 * 1/2 = 15,8114. A probabilidade de haver menos de 548 caras é dada por normdist((548 + 0,5 - 500) / 15,8114) = 0,998920, onde normdist é a função do Excel que calcula a probabilidade de uma variável aleatória com distribuição normal de média 0 e desvio padrão 1 ficar abaixo do valor Z fornecido. Em seguida, subtraímos a probabilidade de haver menos de 452 caras. Isso resulta em normdist((452 - 0,5 - 500) / 15,8114) = 0,001080. Portanto, a resposta é 0,99892 - 0,00108 = 0,997840. Novamente, esta é uma aproximação. A resposta correta é 0,997856, mas é mais trabalhosa de calcular. Em média, depois de estabelecer um ponto no craps, com que frequência o jogador consegue repetir o feito?
Dado que um ponto foi marcado, em 5/12 das vezes será um 6 ou 8, em 4/12 será um 5 ou 9 e em 3/12 será um 4 ou 10. A probabilidade de marcar um 6 ou 8 é 5/11, de marcar um 5 ou 9 é 4/10 e de marcar um 4 ou 10 é 3/9. Portanto, a probabilidade de marcar um ponto, dado que um ponto foi marcado, é (5/12)*(5/11)+(4/12)*(4/10)+(3/12)*(3/9) = 40,61%.
Senhor Mágico, se 50 pessoas diferentes lançarem uma moeda para o ar 8 vezes, qual a porcentagem dessas 50 pessoas que obterão 8 caras ou coroas consecutivas? Agradeço antecipadamente.
A probabilidade de uma pessoa qualquer lançar 8 caras ou coroas é 2*(1/2) 8 = 1 em 128. Se 50 pessoas fizessem isso, em média 0,39 delas obteriam todas as caras ou coroas. A probabilidade de pelo menos uma pessoa obter todas as caras ou coroas é de 32,44%.
Tenho um saco com 100 moedas, e uma delas tem duas caras. Escolho uma moeda aleatoriamente e observo que ela dá 10 caras seguidas. Qual é a probabilidade de eu ter escolhido a moeda com duas caras?
Este é um exemplo clássico de probabilidade condicional Bayesiana. Em geral, a probabilidade de A dado B é a probabilidade de A e B juntos dividida pela probabilidade de B. Neste caso, A está lançando uma moeda com duas caras seguidas e B está lançando uma moeda com duas caras. A probabilidade de A e B juntos é 1/100. Isso ocorre porque há uma chance de 1 em 100 de escolher a moeda com duas caras, e se isso acontecer, a probabilidade de obter 10 caras seguidas é de 100%. A probabilidade de obter 10 caras seguidas, assumindo uma moeda escolhida aleatoriamente, é (1/100)*1 + (99/100)*(1/2) 10 . Isso porque há uma chance de 1% de escolher a moeda com duas caras, que tem 100% de chance de obter 10 caras, e uma chance de 99% de escolher uma moeda honesta, que tem (1/2) 10 de chance de obter 10 caras seguidas. Portanto, a probabilidade de você ter escolhido a moeda de duas caras, dado que você lançou 10 caras seguidas, é 0,01/(0,01*1 + 0,99* 0,000977) = 0,911843.
Você tem alguma dica para apostar no lançamento de uma moeda?
Sim! Meu conselho é apostar no lado que está virado para cima no início do lançamento. De acordo com o Science News Online, a probabilidade de uma moeda cair com o mesmo lado em que começou é de 51%. O artigo diz que isso acontece porque uma moeda lançada não gira perfeitamente em torno do seu eixo e, às vezes, parece estar girando quando na verdade não está. Essa hipótese só se aplica se a moeda for pega na palma da mão, para que o quique não seja um problema. O artigo também afirma que uma moeda girando cairá com a face "coroa" para cima em 80% das vezes, devido ao lado mais pesado, que representa a "cara", tender a cair primeiro. No entanto, estou cético quanto a isso. Tentei 20 vezes e obtive 11 caras e 9 coroas. A probabilidade de obter 9 ou menos coroas em 20 lançamentos, com uma probabilidade de sucesso de 80%, é de 1 em 1775.
Acho que posso ter uma resposta para o mistério da moeda giratória. Há mais de uma década, fiz um projeto de ciências sobre girar uma moeda na sexta série. Li na revista Omni que girar uma moeda muito rápido quase sempre a fará parar com a coroa para cima, porque as laterais se inclinam para a frente. Tentei centenas de vezes e obtive resultados quase imparciais, exceto duas vezes em que ela parou de lado.
Depois de inúmeras horas perdidas, finalmente descobri que estava girando a moeda rápido demais, e uma rotação mais lenta me deu o resultado desejado: coroa para cima. Além disso, a moeda não é completamente uniforme, e começar a girá-la pela parte mais fina pareceu contribuir para a consistência. Alguns gráficos cheios de besteiras e um círculo gigante de papelão decorado como uma moeda me renderam um A em Ciências e notas baixas em todas as outras matérias, já que ignorei completamente minha lição de casa.
Então, provei de forma conclusiva, com um experimento rudimentar realizado há mais de dez anos, do qual mal me lembro de algo e sobre o qual não tinha realmente entendido o que estava fazendo na época, que talvez você esteja girando sua moeda um pouco rápido demais.
Muito bem, tentei novamente, girando a moeda lentamente 100 vezes. Por lentamente, quero dizer que o tempo entre o giro e o momento em que o resultado se tornou óbvio foi de pelo menos dois segundos, mas menos de cinco. Usei uma moeda de um centavo de 2004-D, bem brilhante. Meus resultados foram 52 caras e 48 coroas. Portanto, continuo sem me convencer de que girar uma moeda, em qualquer velocidade, seja altamente tendencioso para dar coroa.
Meu entendimento de "tempo de espera" para um evento é o inverso da probabilidade desse evento. Estou interessado em calcular o tempo de espera para obter dois números consecutivos em um dado. Em uma simulação, obtive uma média de 42 lançamentos. Como posso estabelecer essa relação com a probabilidade de obter dois números consecutivos?
É verdade que, para eventos únicos, se a probabilidade for p, o tempo médio de espera será 1/p. No entanto, a situação se complica com eventos consecutivos. Seja x o estado em que o último lançamento não resultou em dois. Este também é o estado inicial. Seja y o estado em que o último lançamento resultou em dois. Após o primeiro lançamento, há uma probabilidade de 5/6 de ainda estarmos no estado x e 1/6 de estarmos no estado y. Seja Ex(x) o número esperado de lançamentos a partir do estado x e Ex(y) o número esperado a partir do estado y. Então...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y), e
Ex(y) = 1 + (5/6)*ex(x)
Resolvendo essas duas equações...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*( 1 + (5/6)*Ex(x))
Ex(x) = 7/6 + (35/36)*Ex(x)
(1/36)*Ex(x) = 7/6
Ex(x) = 36*(7/6) = 42
Assim, o tempo médio de espera para dois números dois consecutivos é de 42 lançamentos.
Eu tenho o mesmo tipo de problema, só que com os lançamentos esperados para se obter duas caras, no meu site de problemas de matemática , veja o problema 128.
Suponha que temos um jogo de azar. Uma moeda não viciada é lançada repetidamente. Para cada lançamento, temos que pagar 1 rupia. Existem dois resultados possíveis: cara (H) ou coroa (T). Se a diferença entre cara e coroa for 3, receberemos 8 rupias do apostador. Devemos jogar? Por quê? Qual é a nossa probabilidade de ganhar? Qual seria o impacto na probabilidade de ganhar se recebêssemos 7 ou 9 rupias?
Vamos chamar de x o número esperado de lançamentos a partir do ponto inicial.
Vamos chamar de y o número esperado de lançamentos restantes se um lado estiver com um lançamento a mais que o outro.
Vamos chamar de z o número esperado de lançamentos restantes se um dos lados estiver com dois lançamentos a mais que o outro.
E(x) = 1 + E(y)
E(y) = 1 + 0,5*E(x) + 0,5*E(z)
E(z) = 1 + 0,5*E(y)
É fácil perceber, por meio de álgebra matricial, que E(x) = 9, E(y) = 8 e E(z) = 5. Portanto, em média, serão necessárias 9 jogadas para que a diferença entre cara e coroa seja de 3. Assim, com uma aposta de 8 rúpias, é uma boa aposta para quem recebe uma rúpia por jogada, pois receberá em média 9 rúpias, mas terá um retorno de apenas 8. A vantagem da casa para o apostador é de 11,11%. Com 9 rúpias, é uma aposta justa; com 7 rúpias, a vantagem da casa é de 22,22%.
Na sua coluna "Pergunte ao Mago" de 13 de março de 2006 , você apresentou três fórmulas para o jogo da "rupia". Embora a solução esteja matematicamente correta, não consigo entender como as três equações modelam o problema. Você poderia explicar como chegou a essas três equações?
Várias pessoas me pediram para explicar melhor minha resposta. A solução requer álgebra matricial básica.
Comece definindo x como a resposta, ou o número médio de lançamentos até que a diferença entre caras e coroas seja 3.
Seja y o número esperado de lançamentos a partir de um ponto em que um lado está para cima por um lançamento.
Seja z o número esperado de lançamentos a partir de um ponto em que um lado está para cima, com uma diferença de dois lançamentos.
Após o primeiro lançamento, um dos lados estará em maioria por uma única jogada. Portanto, x = 1 + y.
Quando um dos lados está com uma vantagem de um lance, outro lance resultará no estado inicial de empate ou em um dos lados ficando com uma vantagem de dois lances. Ambos os resultados são igualmente prováveis. Portanto, y = 1 + 0,5x + 0,5z
Quando um dos lados estiver com duas jogadas de vantagem, outra jogada resultará em um dos lados ficando com uma jogada de vantagem ou no fim do jogo. Novamente, ambos os resultados são igualmente prováveis. Portanto, z = 1 + 0,5 * y
Temos, portanto, três equações e três incógnitas:
(1) X = 1 + y
(2) Y = 1 + 0,5x + 0,5z
(3) Z = 1 + 0,5y
Para resolver, vamos primeiro eliminar as casas decimais multiplicando as duas últimas equações por 2.
(1) X = 1 + y
(2) 2Y = 2 + x + z
(3) 2Z = 2 + y
Vamos substituir 1+y, de (1) por x em (2).
2Y = 2 + 1 + y + z
(4) y = 3 + z
Não há substituto 3+z para y em (3)
2z = 2 + 3 + z
z = 5
Agora substitua 5 por z em (4) para obter
(5) y = 3 + 5 = 8
Não há substituto y = 8 em (1) para obter
(6) x = 9
Um amigo escolhe uma sequência de 3 lançamentos de moeda, cara ou coroa, e me dá a opção de escolher minha própria sequência (diferente) de 3 lançamentos. Lançamos uma moeda honesta quantas vezes forem necessárias até que uma das nossas sequências seja escolhida. Se ele escolher HHH (cara, coroa e coroa), qual sequência eu devo escolher e qual é a minha vantagem nessa aposta? Como eu calculo qual sequência escolher com base na sequência escolhida por ele?
A tabela a seguir mostra a probabilidade de o jogador A vencer de acordo com todos os padrões possíveis escolhidos pelos jogadores A e B.
Probabilidade de o jogador A vencer
| Jogador A | Jogador B | |||||||
| HHH | HHT | HTH | HTT | THH | THT | TTH | TTT | |
| HHH | 1/2 | 2/5 | 2/5 | 1/8 | 5/12 | 3/10 | 1/2 | |
| HHT | 1/2 | 2/3 | 2/3 | 1/4 | 5/8 | 1/2 | 7/10 | |
| HTH | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/8 | 7/12 | |
| HTT | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/4 | 7/8 | |
| THH | 7/8 | 3/4 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| THT | 7/12 | 3/8 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| TTH | 7/10 | 1/2 | 5/8 | 1/4 | 2/3 | 2/3 | 1/2 | |
| TTT | 1/2 | 3/10 | 5/12 | 1/8 | 2/5 | 2/5 | 1/2 | |
Uma técnica de memorização para selecionar o padrão ideal é usar a seguinte estratégia: a primeira e a segunda escolhas do seu oponente devem ser, respectivamente, a sua segunda e a terceira. Sua primeira escolha deve ser o oposto da sua terceira. Por exemplo, se o seu oponente escolher HTT, sua segunda e terceira escolhas devem ser HT. Sua última escolha é T, então sua primeira escolha deve ser H, para um padrão HHT. Seguindo essa estratégia, sua probabilidade de vitória será de 2/3 a 7/8, dependendo do padrão escolhido pelo seu oponente.
Olá, meu nome é Patty. Você tem um site muito bom e parece ser um homem muito inteligente. Definitivamente o tipo de homem que eu quero ao meu lado em um cassino! Gostaria de saber se você poderia me ajudar. Comentei com meu namorado que procuraria a resposta para um problema na internet. Se você me ajudasse, eu ficaria muito bem na fita.
Meu namorado coleciona moedas. Ele comprou um saco de moedas de um centavo de trigo. Eu não entendo muito de moedas (ele está me ensinando aos poucos). Mas ele disse que ficou impressionado por não haver moedas de um determinado ano no saco, já que são tão comuns. Ele disse que a probabilidade disso acontecer era de uma em um bilhão. Eu disse a ele que tentaria perguntar para as pessoas do meu escritório (os autoproclamados gênios!!) e, se elas não soubessem, eu faria uma pesquisa online. Foi assim que encontrei vocês.
Enfim, se puder ajudar, agradeceria muito. O saco tinha aproximadamente 5.500 moedas de um centavo. O total de moedas de um centavo com a imagem do trigo cunhadas por todas as casas da moeda dos EUA foi de 24.267.000.000. O número de moedas de 1955 cunhadas (a que ele estava procurando) foi de 330.000.000. Alguns colegas do meu escritório dizem que existem outros fatores, como demografia, o fato de as casas da moeda poderem não ter distribuído todas as moedas, etc. ...................... Eu presumo que eles estejam certos, mas eu (e tenho certeza que meu namorado também) preferiria saber as probabilidades aproximadas! Espero que você possa ajudar.
Seus números de cunhagem são próximos aos da Mountain View Coins . Supondo que cada centavo de trigo já cunhado tenha a mesma probabilidade de estar no saco, a probabilidade de qualquer centavo não ser um 55 é (24.267.000.000 - 330.000.000) / 24.267.000.000 = 0,986401286. A probabilidade de 5.500 moedas não serem um 55 pode ser aproximada com bastante precisão por 0,986401286. 5.500 = 1 em 507.033.772.284.213.000.000.000.000.000.000.
Meu pai é colecionador de moedas, então pedi a ajuda dele para esta. Eis o que ele disse:
Eis o meu palpite. No ano de 1955, um pequeno número de moedas de um centavo de Lincoln foi cunhado na Filadélfia com a data impressa duas vezes. Ninguém sabe exatamente quantas foram misturadas com outras moedas de um centavo para circulação antes que o erro fosse descoberto. Um exemplar não circulado hoje vale entre US$ 2.000 e US$ 6.000. Suspeito que o saco de moedas de um centavo de 1955 já tenha sido esvaziado por alguém procurando por exemplares com cunhagem dupla. Aqui está a foto de uma delas: Moeda de um centavo de 1955 com cunhagem dupla no anverso .
Note que este site vende moedas de um centavo com a imagem de trigo, e pode apostar que já houve uma seleção de datas após as moedas terem sido coletadas pelo revendedor. Eu imaginaria que as moedas de 1955 que não eram de cunhagem dupla teriam sido devolvidas à coleção, mas talvez sejam vendidas separadamente ou derretidas. O cobre nas moedas de um centavo com a imagem de trigo vale muito mais do que um centavo hoje em dia. É por isso que mudaram para moedas de um centavo de zinco revestidas de cobre algumas décadas atrás. Existe a possibilidade de a própria Casa da Moeda ter decidido não distribuir muitas das moedas de 1955 e tê-las derretido após a cunhagem para evitar uma corrida frenética pelos raros exemplares de cunhagem dupla. A Casa da Moeda e os Correios sempre se sentiram constrangidos com erros de impressão e tentam mantê-los fora de circulação.
Na sua última coluna, você disse que "A probabilidade de 5500 moedas não serem de valor 55 pode ser aproximada com muita precisão por 0,9864012865500 = 1 em 507.033.772.284.213.000.000.000.000.000.000."
Presumo que seja "aproximado" devido ao efeito da remoção ao longo das 5500 moedas. Que efeito minúsculo da remoção! Este é um bom exemplo de como a probabilidade de obter as moedas-alvo diminui à medida que se removem as moedas que não são alvo, porque o efeito da remoção é muito pequeno em comparação com a probabilidade muito maior de um jogo fraudulento, ou seja, de as moedas-alvo terem sido removidas.
Sim, eu disse "aproximadamente" porque existem apenas algumas moedas de um centavo no mundo. Remova uma moeda que não seja de 55 centavos do saco e o efeito dessa remoção aumenta a probabilidade de que todas as outras moedas no saco sejam de 55 centavos. Se eu não tivesse dito "aproximadamente", pelo menos três pessoas teriam me escrito para me corrigir. É claro que é um efeito extremamente pequeno, mas muitos dos meus leitores são perfeccionistas e me criticam duramente pelo menor dos erros.
Há duas mesas em uma sala. Na mesa da direita, há 100 moedas, sendo 20 com o "H" virado para cima e as 80 restantes com o "T" virado para cima. Não há moedas na outra mesa. O objetivo é mover as moedas de forma que haja um número igual de moedas com o "H" virado para cima em ambas as mesas. Você não pode ver as moedas (a sala está escura) nem tocá-las para saber se estão viradas para cima ou para baixo.
Acesse meu outro site, mathproblems.info, para ver a solução (aviso de spoiler!).
Meu amigo me ofereceu uma aposta de 20 dólares, com uma probabilidade de 3 para 1 de que, se eu jogasse uma moeda 100 vezes, sairia exatamente 50 caras e 50 coroas. Se desse certo, eu ganharia 60 dólares, e se não, ficaria devendo 20 dólares. Eu deveria ter aceitado a aposta? Além disso, se 50/50 não é o resultado mais provável, existe algum outro resultado (como 51/49) que seja mais provável?
A probabilidade de obter exatamente 50 de cada é combin (100,50)*(1/2) 100 = 7,96%. Uma probabilidade justa seria de 11,56 para 1. Portanto, com uma probabilidade de 3 para 1, é uma aposta péssima, com uma vantagem da casa de 68,2%. Que amigo você tem! 50/50 é a divisão exata mais provável entre caras e coroas. Uma aposta interessante é se o número de caras/coroas ficará entre 47 e 53, ou não. A probabilidade de ficar dentro desse intervalo é de 51,59%. Se você conseguir encontrar alguém para apostar que o total ficará fora desse intervalo, então, com uma probabilidade de 1 para 1, você teria uma vantagem de 3,18%.
A tabela a seguir mostra a probabilidade para cada um dos resultados de 30 a 70 caras/coroas.
Probabilidade de obter o total de caras/coroas em 100 lançamentos
| Cara ou coroa | Probabilidade |
|---|---|
| 30, 70 | 0,000023 |
| 31, 69 | 0,000052 |
| 32, 68 | 0,000113 |
| 33, 67 | 0,000232 |
| 34, 66 | 0,000458 |
| 35, 65 | 0,000864 |
| 36, 64 | 0,001560 |
| 37, 63 | 0,002698 |
| 38, 62 | 0,004473 |
| 39, 61 | 0,007111 |
| 40, 60 | 0,010844 |
| 41, 59 | 0,015869 |
| 42, 58 | 0,022292 |
| 43, 57 | 0,030069 |
| 44, 56 | 0,038953 |
| 45, 55 | 0,048474 |
| 46, 54 | 0,057958 |
| 47, 53 | 0,066590 |
| 48, 52 | 0,073527 |
| 49, 51 | 0,078029 |
| 50 | 0,079589 |
A fórmula geral para a probabilidade de w vitórias em n tentativas, onde a probabilidade de cada vitória é p, é combin(n,w) × p w × (1-p) (nw) = [n!/(w! × (nw)!] × p w × (1-p) (nw) .
Se eu lançar uma moeda 1.000 vezes, qual é a probabilidade de obter uma sequência de pelo menos 10 caras ou coroas consecutivas?
Que coincidência você perguntar isso; outro leitor acabou de me enviar um artigo acadêmico sobre esse assunto. Esse artigo inclui o seguinte gráfico, que mostra que a probabilidade é de cerca de 62%.
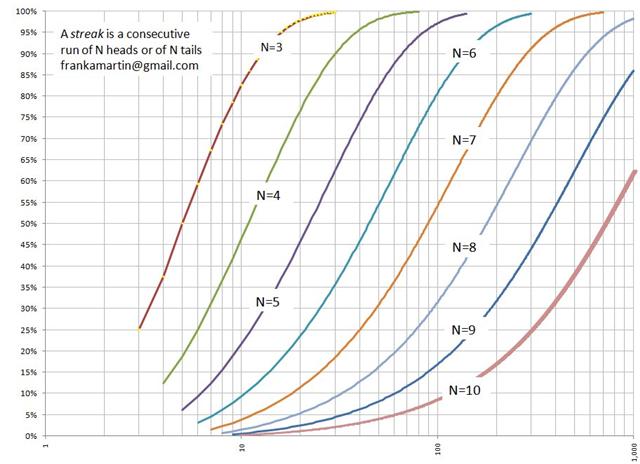
Para mais informações sobre este tópico, visite What were the Odds of Having Such a Terrible Streak at the Casino? (483K) de Frank Martin.
Se uma moeda for lançada 100 vezes, qual é a probabilidade de se obter uma sequência de pelo menos 7 caras consecutivas pelo menos uma vez?
Se existe uma expressão simples e não recursiva para a resposta, eu desconheço. No entanto, existe uma resposta recursiva simples.
f(n) = pr(cara no primeiro lançamento) × f(n-1) +
pr(cara no primeiro lançamento, coroa no segundo lançamento)×f(n-2) +
pr(cara nos dois primeiros lançamentos, coroa no terceiro lançamento)×f(n-3) +
pr(cara nos primeiros 3 lançamentos, coroa no terceiro lançamento)×f(n-4) +
pr(cara nos primeiros 4 lançamentos, coroa no quarto lançamento)×f(n-5) +
pr(caras nos primeiros 5 lançamentos, coroas no quinto lançamento)×f(n-6) +
pr(caras nos primeiros 6 lançamentos, coroas no sexto lançamento)×f(n-7) +
pr(caras nos primeiros 7 lançamentos) =
(1/2)×f(n-1) +
(1/2) 2 ×f(n-2) +
(1/2) 3 ×f(n-3) +
(1/2) 4 ×f(n-4) +
(1/2) 5 ×f(n-5) +
(1/2) 6 ×f(n-6) +
(1/2) 7 ×f(n-7) +
(1/2) 7
Onde:
f(n) = probabilidade de sucesso em n lançamentos.
pr(x) = probabilidade de x acontecer.
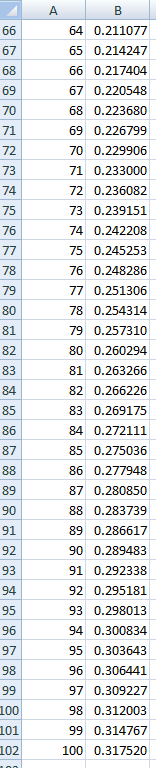
Planilhas são perfeitas para problemas como este. Nas capturas de tela da planilha abaixo, inseri uma probabilidade de 0 para as células de B2 a B8, porque não é possível obter 7 caras seguidas em 6 ou menos lançamentos. Para a célula B9, inseri a fórmula:
=(1/2)*B8+(1/2)^2*B7+(1/2)^3*B6+(1/2)^4*B5+(1/2)^5*B4+(1/2)^6*B3+(1/2)^7*B2+(1/2)^7
Em seguida, copiei e colei o valor das células B10 para as células B102, o que corresponde a 100 inversões. Essa probabilidade é de 0,317520. Uma simulação aleatória confirma isso.
 |  |
Após a publicação original deste texto, Rick Percy compartilhou comigo sua solução em álgebra matricial. Aqui está ela, em minhas próprias palavras. Pressupõe-se que o leitor já conheça os conceitos básicos de álgebra matricial.
Primeiro, existem oito estados possíveis em que o flipper pode estar em qualquer momento:
p 1 = Probabilidade de sucesso, dado que você precisa de mais 7 cabeças a partir do ponto atual.
p 2 = Probabilidade de sucesso, dado que você precisa de mais 6 cabeças a partir do ponto atual.
p 3 = Probabilidade de sucesso, dado que você precisa de mais 5 cabeças a partir do ponto atual.
p 4 = Probabilidade de sucesso, dado que você precisa de mais 4 cabeças a partir do ponto atual.
p 5 = Probabilidade de sucesso, dado que você precisa de mais 3 cabeças a partir do ponto atual.
p 6 = Probabilidade de sucesso, dado que você precisa de mais 2 cabeças a partir do ponto atual.
p 7 = Probabilidade de sucesso, dado que você precisa de mais 1 cara a partir do ponto atual.
p 8 = Probabilidade de sucesso, dado que você não precisa de mais caras = 1.
Vamos definir a matriz S<sub> n</sub> como a probabilidade de estar em cada estado após o n -ésimo lançamento. S <sub>0</sub> representa as probabilidades antes do primeiro lançamento, onde há 100% de chance de estar no estado 0. Portanto, S <sub>0 </sub> =
| 1 0 0 0 0 0 0 0 |
Seja T a matriz de transformação de duas inversões consecutivas, ou seja, de S n para S n+1 , onde S n+1 = T × S n
- Se você estiver no estado 1, após um lançamento de moeda você tem 0,5 de chance de estar no estado 2 (com cara) e 0,5 de permanecer no estado 1 (com coroa).
- Se você estiver no estado 2, após um lançamento de moeda você tem 0,5 de chance de estar no estado 3 (com cara) e 0,5 de chance de retornar ao estado 1 (com coroa).
- Se você estiver no estado 3, após um lançamento de moeda você tem 0,5 de chance de estar no estado 4 (com cara) e 0,5 de chance de retornar ao estado 1 (com coroa).
- Se você estiver no estado 4, após um lançamento de moeda você terá 0,5 de chance de estar no estado 5 (com cara) e 0,5 de chance de retornar ao estado 1 (com coroa).
- Se você estiver no estado 5, após um lançamento de moeda você tem 0,5 de chance de estar no estado 6 (com cara) e 0,5 de chance de retornar ao estado 1 (com coroa).
- Se você estiver no estado 6, após um lançamento de moeda você tem 0,5 de chance de estar no estado 7 (com cara) e 0,5 de chance de retornar ao estado 1 (com coroa).
- Se você estiver no estado 7, após um lançamento de moeda você terá 0,5 de chance de estar no estado 8 (com cara) e 0,5 de chance de retornar ao estado 1 (com coroa).
- Se você estiver no estado 8, significa que obteve sucesso e permanecerá no estado 8 com uma probabilidade de 1,0.
Colocando tudo isso na forma da matriz de transição T =
| 0,5 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,5 0,0 0,0 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,5 0,0 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,5 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,5 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,0 0,5 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,5 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,5 |
| 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 1,0 |
Para chegar à probabilidade de cada estado após um lançamento...
(1) S 1 = S 0 × T
E depois de duas viradas?
(2) S 2 = S 1 × T
Vamos substituir a equação (1) na equação (2)...
(3) S 2 = S 0 × T × T = S 0 × T 2
E depois de 3 flips?
(4) S 3 = S 2 × T
Substituindo a equação (3) em (4)...
(5) S 3 = S 0 × T 2 × T = S 0 × T 3
Podemos continuar fazendo isso até chegar ao estado depois da centésima virada...
S 100 = S 0 × T 100
Então, o que é T 100 ? Antes dos computadores, devia ser uma tarefa extremamente difícil descobrir essas coisas. No entanto, com a função MMULT do Excel e muita cópia e colagem, descobrimos que T 100 =
| 0,342616 0,171999 0,086347 0,043347 0,021761 0,010924 0,005484 0,317520 |
| 0,339863 0,170617 0,085653 0,042999 0,021586 0,010837 0,005440 0,323005 |
| 0,334379 0,167864 0,084271 0,042305 0,021238 0,010662 0,005352 0,333929 |
| 0,323454 0,162380 0,081517 0,040923 0,020544 0,010313 0,005178 0,355690 |
| 0,301693 0,151455 0,076033 0,038170 0,019162 0,009620 0,004829 0,399038 |
| 0,258346 0,129694 0,065109 0.032686 0,016409 0,008237 0,004135 0,485384 |
| 0,171999 0,086347 0,043347 0,021761 0,010924 0,005484 0,002753 0,657384 |
| 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 1,000000 |
O termo no canto superior direito mostra a probabilidade de estar no estado 8 após 100 lançamentos, que é 0,317520.
Você já ouviu a história do jogador de críquete australiano que errou o resultado do lançamento de uma moeda por 35 jogos seguidos, antes de acertar o 36º? Qual a probabilidade disso acontecer?
Eu não tinha ouvido falar disso até você mencionar. Você está se referindo à incrível história de Kristy Perrin , uma jogadora de críquete adolescente do Magpies, que errou o resultado do lançamento da moeda 35 vezes seguidas. A probabilidade de errar exatamente 35 ou mais lançamentos é (1/2) 35 = 1 em 34.359.738.368. Para se ter uma ideia, a probabilidade de ganhar na Powerball é de 1 em 195.249.054. Isso é 176 vezes mais provável do que errar 35 lançamentos de moeda consecutivos.
Você tem alguma dica para apostar no lançamento de uma moeda?
Sim! Aposte no lado que estiver virado para cima na mão de quem está lançando a moeda. O artigo acadêmico "Dynamic Bias in the Coin Toss" ( Viés Dinâmico no Lançamento de Moedas), de Persi Diaconis, Susan Holmes e Richard Montgomery, conclui que a moeda cairá no mesmo lado em que começou em 51% das vezes.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Em média, quantas tentativas serão necessárias em um jogo 50/50 para perder duas seguidas? E se forem 3, 4 ou n tentativas seguidas?
Vamos resolver primeiro o caso com duas perdas.
Seja x o número esperado de lançamentos futuros, começando do início ou após qualquer vitória.
Seja y o número esperado de lançamentos futuros após uma perda.
Podemos formular as seguintes duas equações:
(1) x = 1 + 0,5x + 0,5y
O número um representa que o jogador deve lançar a moeda para mudar de estado. Há 50% de chance de vitória, permanecendo no estado x. Há 50% de chance de derrota, avançando para o estado y.
(2) y = 1 + 0,5x
Partindo do estado y novamente, o 1 representa o lançamento da moeda naquele ponto. Há 50% de chance de vitória, retornando ao estado x. Há 50% de chance de derrota, encerrando o jogo e não sendo necessários lançamentos adicionais, portanto, o resultado implícito é 0,5*0.
Multiplique ambas as equações por 2 e reorganize-as para obter:
(3) x - y = 2
(4) -x + 2y = 2
Some as duas equações para obter:
(5) y = 4
Substitua isso em qualquer equação de (1) a (4) e obtenha x=6.
Para o caso de três perdas, defina os três estados possíveis como:
Seja x o número esperado de lançamentos futuros, começando do início ou após qualquer vitória.
Seja y o número esperado de lançamentos futuros após uma perda.
Seja z o número esperado de lançamentos de moeda futuros após duas perdas.
As equações iniciais são:
x = 1 + 0,5x + 0,5y
y = 1 + 0,5x + 0,5z
z = 1 + 0,5x
Podemos definir os estados iniciais em forma matricial da seguinte maneira:
| 0,5 | -0,5 | 0 | 1 |
| -0,5 | 1 | -0,5 | 1 |
| -0,5 | 0 | 1 | 1 |
Se você se lembra da álgebra matricial, podemos resolver para x como determinante(A)/determinante(B), onde
Um =
| 1 | -0,5 | 0 |
| 1 | 1 | -0,5 |
| 1 | 0 | 1 |
B =
| 0,5 | -0,5 | 0 |
| -0,5 | 1 | -0,5 |
| -0,5 | 0 | 1 |
| 0,5 | -0,5 | 0 |
| -0,5 | 1 | -0,5 |
| -0,5 | 0 | 1 |
O Excel possui uma função determinante muito útil: =mdeterm(intervalo). Neste caso, x = mdeterm(matriz A)/mdeterm(matriz B) = 1,75/0,125 = 14.
Podemos usar recursão para perdas consecutivas adicionais. Vamos considerar o caso 4. Sabemos, pelo que vimos acima, que serão necessárias, em média, 14 jogadas para obter 3 perdas seguidas. Nesse ponto, a moeda será lançada novamente, com 50% de chance de recomeçar. Portanto:
x = 14 + 1 + x/2
x/2 = 15
x = 30
Em outras palavras, adicione um à resposta anterior e depois dobre o resultado.
Não é difícil perceber o padrão. O número esperado de lançamentos para obter n derrotas seguidas é 2^ n + 1 - 2.
Essa questão foi levantada e discutida no meu fórum, Wizard of Vegas .
Dado que uma moeda honesta é lançada n vezes, qual é a probabilidade de se obter pelo menos uma sequência de t caras?
A resposta é 1-F (t) n+2 /2 n , onde F (t) n é o n-ésimo número em uma sequência de Fibonacci de t passos.
O que é uma sequência de Fibonacci, você pode perguntar? O primeiro número é um. Em uma sequência de t passos, cada número subsequente é a soma dos t números anteriores. Considere que qualquer número antes do primeiro é zero.
Vamos analisar uma sequência de dois passos. O primeiro número é 1. O segundo é a soma dos dois números anteriores. Suponha que haja um zero antes do um, então o segundo número é 0 + 1 = 1. O terceiro número é 1 + 1 = 2, o quarto é 1 + 2 = 3 e o quinto é 2 + 3 = 5.
Os primeiros doze números de Fibonacci de dois passos são: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144.
Vamos a um exemplo. Qual é a probabilidade de se obter duas caras consecutivas pelo menos uma vez em dez lançamentos?
Usamos a sequência de Fibonacci de dois passos, porque precisamos apenas de duas caras. O 12º número na sequência (dois a mais que o número de lançamentos) é 144. Portanto, a resposta é 1-F (2) 10+2 /2 10 = 1 - 144/2 10 = 1 - 144/1024 = 85,94%.
Qual a probabilidade de se obter cinco caras consecutivas em 20 lançamentos de moeda?
Os primeiros 22 números de Fibonacci de 5 passos são 1, 1, 2, 4, 8, 16, 31, 61, 120, 236, 464, 912, 1793, 3525, 6930, 13624, 26784, 52656, 103519, 203513, 400096, 786568.
A resposta é, portanto, 1 - F (5) 20+2 /2 20 = 1 - 786.568/1.048.576 = 1 - 75,01% = 24,99%.
Essa questão é discutida no meu fórum, Wizard of Vegas .
Há uma moeda viciada com 60% de chance de cair em cara. Ela é lançada até que haja duas caras ou duas coroas seguidas. Qual é a probabilidade de sair duas caras primeiro?
Aqui está a resposta e a solução (PDF).
Para discutir esse problema, visite meu fórum no Wizard of Vegas .
Mago, desafio você para uma aposta. Eis as regras:
- Você escolhe qualquer padrão que desejar de caras (H) e coroas (T). Por exemplo, HTT.
- Após revelar seu padrão, escolherei o meu.
- Vamos lançar uma moeda repetidamente até que um padrão apareça na ordem correta. Quem escolheu esse padrão ganha.
- Eu te dou uma aposta de 3 para 2.
Você aceita? Farei isso quantas vezes você quiser.
Não. Boa tentativa, no entanto. A pessoa que age em segundo lugar tem uma enorme vantagem posicional. Aqui está a estratégia para a pessoa que age em segundo lugar e sua probabilidade de vitória.
Estratégia do Jogo Odiusgambit
| Jogador 1 | Jogador 2 | Jogador 2 vence |
|---|---|---|
| HHH | THH | 87,50% |
| HHT | THH | 75,00% |
| HTH | HHT | 66,67% |
| HHT | THH | 75,00% |
| THH | HTT | 75,00% |
| THT | TTH | 66,67% |
| TTH | HTT | 75,00% |
| TTT | HTT | 87,50% |
Como mostra a tabela acima, minha melhor chance de ganhar, ou a sua pior, é se eu escolher THT ou HTH, onde minha chance de ganhar ainda é de apenas 1 em 3. Eu deveria ter uma probabilidade de 2 para 1 para que fosse uma aposta justa, então, com apenas 3 para 2, você tem uma vantagem de 16,67%.
Aqui está uma maneira de lembrar a estratégia do jogador dois. Seja P(x) a escolha do jogador 1 para a posição x. Seja O(x) o oposto da escolha do jogador 1 para a posição x. O jogador 2 deve sempre escolher: O(2) - P(1) - P(2).
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Se você lançar uma moeda honesta 40 vezes, qual é a probabilidade de obter uma sequência de 5 caras e uma sequência de 5 coroas? "Sequência" significa pelo menos 1 e "5" significa pelo menos 5. As sequências de caras e coroas não precisam ser adjacentes.
Por favor, clique no botão abaixo para ver a resposta.
Aqui está minha solução (PDF).
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Henry e Tom decidem apostar no cara ou coroa. Henry ganha se der cara, Tom ganha se der coroa.
Cada lançamento custa US$ 1 e, como estão muito entediados, decidem fazer um milhão de lançamentos. Ao final da sessão, o perdedor pagará ao vencedor o saldo final por meio de um cheque. Qual é o valor esperado do cheque?
A fórmula geral para a resposta é sqrt(variância * (2/pi)).
A variância neste caso é 1.000.000. Portanto, a diferença absoluta esperada entre os resultados reais e os esperados é sqrt(1.000.000 × (2/pi)) =~ 797,88456080286535587989211986876373695171726 232986931533185165934131585179860367700250466 781461387286060511772527036537102198390911167 448599242546125101541269054116544099863512903 269161506119450728546416733918695654340599837 28381269120656178667772134093073.
Eu faço uma pergunta relacionada em Ask the Wizard #358 , que ajudará a mostrar de onde vem o termo sqrt(2/pi).
Essa pergunta foi feita e discutida no fórum do Wizard of Vegas .
Suponha que um cassino tenha um jogo baseado no lançamento de uma moeda honesta que paga o mesmo valor apostado. Um jogador deseja jogar um milhão de vezes com uma aposta de $1. Quanto dinheiro ele deve levar para a mesa para ter 50% de chance de não perder tudo?
Vamos primeiro responder à pergunta: qual é a probabilidade de o jogador ficar com um prejuízo superior a x unidades após um milhão de lançamentos, assumindo que ele tenha uma banca ilimitada?
Como se trata de uma aposta justa, o ganho médio após um milhão de lançamentos é zero. A variância de cada lançamento é 1, portanto a variância de um milhão de lançamentos é um milhão. Um desvio padrão é, portanto, sqrt(1.000.000) = 1000.
Podemos calcular a banca necessária com a função do Excel =NORM.INV(probabilidade;média;desvio padrão). Por exemplo, se usarmos =NORM.INV(0,25;0;1000), obtemos -674,49. Isso significa que, após um milhão de lançamentos, o jogador tem 25% de chance de perder 674 ou mais. Lembre-se de que esta é uma estimativa. Para obter um resultado preciso, deveríamos usar a distribuição binomial, o que seria muito trabalhoso com um milhão de lançamentos.
É bem possível que, se o jogador levar $674 para a mesa, ele fique sem dinheiro antes de ganhar o milhão. Se ele puder continuar jogando a crédito, pode ser que consiga se recuperar e termine com um prejuízo de menos de $674. Aliás, uma vez que o jogador esteja com -674, há 50% de chance de ele terminar com um saldo positivo ou negativo de -674 em qualquer momento futuro.
Portanto, se o jogador puder jogar a crédito, existem três resultados possíveis.
- O jogador nunca fica abaixo de -674.
- O jogador chega a ficar com um placar abaixo de -674 em algum momento, mas se recupera e termina acima de -674.
- Em algum momento, o jogador cai abaixo de -674, continua jogando e perde ainda mais.
Estabelecemos que o cenário 3 tem uma probabilidade de 25%.
O cenário 2 deve ter a mesma probabilidade que o cenário 3, porque uma vez que o jogador esteja com um saldo negativo de -674, ele tem 50% de chance de terminar acima ou abaixo desse ponto após um milhão de lançamentos de moeda.
O cenário 1 é a única outra alternativa, que deve ter probabilidade de 100%-25%-25% = 50%.
Se a probabilidade de o jogador nunca ficar abaixo de 674 for de 50%, então a alternativa de ficar abaixo desse valor deve ser de 100% - 50% = 50%.
Portanto, essa é a nossa resposta para a pergunta original: 674 dólares.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .


