Roleta - Perguntas gerais
Se alguém apostar em duas colunas na roleta, a probabilidade de ganhar será de 24/38, ou 63%. Essa me parece uma estratégia vencedora. Qual a sua opinião?
Na roleta, qualquer aposta ou combinação de apostas tem uma alta vantagem da casa. Quanto maior a probabilidade de ganhar, mais você terá que arriscar em relação à recompensa. Se você fizer isso 10 vezes, a probabilidade de obter lucro é de 46,42%. Com 100 apostas, a probabilidade cai para 24,6%.
Gostei do seu artigo sobre o sistema de apostas de cancelamento . Que tipo de sistema de cancelamento você seguiria se, em vez de apostar no preto ou no vermelho, você fizesse uma aposta (do mesmo valor) em dois dos três blocos que cobrem 12 números (por exemplo: de 1 a 12 e de 25 a 36) em cada lançamento?
Comece da mesma forma que expliquei para apostas com probabilidades iguais. Cada aposta deve ser a soma dos números da esquerda e da direita. No entanto, seguindo sua estratégia de duas colunas, você deve adicionar o dobro do valor à direita se perder.
O site www.ccc-casino.com oferece roleta sem zero, chamada Super Chance Roulette. Existem sistemas eficazes para jogar sem o zero? Sem o zero, seria possível jogar tanto no preto quanto no vermelho simultaneamente, já que não há o risco de perder o zero?
Joguei no modo de prática e parece ser uma roleta legítima sem zero. Não existe nenhum sistema que possa vencer ou perder neste jogo a longo prazo. Quanto mais você joga, mais a proporção entre o lucro líquido e o valor total apostado se aproxima de zero.
Atualização: Este cassino já fechou.
Duas perguntas para você:
1) Em relação às estratégias básicas de blackjack, você tem estratégias para diferentes grupos de cassinos online. Especificamente, dois grupos diferentes que usam um único baralho: Microgaming e Unified Gaming. Não entendo por que você lista 11 contra 10 como uma aposta para a Microgaming, mas como uma dobra para a Unified. Já que ambos usam um único baralho, parece que a mesma estratégia deveria ser usada. Eu perco mais vezes do que ganho quando dobro essa aposta.
2) Na roleta, parece-me que suas chances seriam melhores apostando igualmente no vermelho e na terceira coluna, ou no preto e na terceira coluna. A terceira coluna tem, se não me engano, 8 vermelhos e apenas 4 pretos. Por outro lado, a primeira coluna tem mais pretos. Apostar dessa forma diminui a vantagem da casa?
Se você dobrar a aposta com 11 em um cassino Microgaming e o dealer fizer um blackjack, você perderá o valor total apostado. No Unified Gaming, o blackjack seria revelado imediatamente se a carta aberta fosse um dez, então não há risco de perder para um blackjack ao dobrar a aposta nessa situação.
Todas as combinações de apostas na roleta produzem o mesmo retorno esperado, assumindo que a temida combinação de cinco números seja evitada. Você está certo ao afirmar que a terceira coluna tem oito vermelhos e quatro pretos. A probabilidade de ganhar 3 unidades é 8/38, 1 unidade é 4/38, empatar é 10/38 e perder 2 unidades é 16/38. O retorno esperado combinado por unidade apostada é (1/2)*(3*8 + 1*4 + 0*10 + 2*16)/38 = -2/38. Apostando no preto e na terceira coluna, a probabilidade de ganhar 3 unidades é 4/38, 1 unidade é 8/38, empatar é 14/38 e perder 2 unidades é 12/38. O retorno esperado é (1/2)*(3*4 + 1*8 + 0*14 + 2*12)/38 = -2/38. Ambas as combinações ponderam os vários resultados de forma diferente, mas a média resulta no mesmo número.
Olá, Wiz. Estou curioso para saber qual é o número esperado de giros em uma roleta americana antes que todos os 38 números sejam escolhidos pelo menos uma vez. Isso é proporcional ao número de seleções (38) ou é exponencialmente relacionado a esse número? Tentei calcular isso para um dado de 6 lados, mas travei rapidamente.
Depois de obter n números, a probabilidade de obter um novo número na próxima rodada é (38-n)/38. Se a probabilidade de um evento é p, então o número esperado de tentativas antes que ele aconteça é 1/p. Assim, o número esperado de rodadas para obter um novo número, dado que você já tem n números, é 38/(38-n). Por exemplo, depois de obter 20 números, o número esperado de rodadas para obter o 21º é 38/18 = 2,11. Portanto, a resposta é a soma do número esperado de rodadas em cada etapa: (38/38) + (38/37) + (38/36) + ... + (38/1) = 160,66.
Qual seria a probabilidade de um número vermelho aparecer 18 vezes seguidas na roleta?
(18/38) 18 =~ 1 em 693745.
Fiquei fascinado ao ler seu comentário sobre as bolinhas de aço não terem memória. Tenho uma roleta em casa e as bolinhas pulam de alegria quando volto do hospital. É óbvio que elas se lembram de mim, e além disso, acho que ficariam ofendidas com seus comentários. No meu planeta, a roleta é proibida porque as bolinhas podem ser subornadas com muita facilidade. Acho seu planeta um lixo e agora não tenho dinheiro para consertar minha nave espacial e voltar para casa.
Ah, e o homem de jaleco branco atrás de mim quer dizer que adora o seu site e agradece todo o trabalho que você dedicou para mostrar os cálculos. Ele disse que isso lhe economizou muito tempo e dinheiro. Continue com o bom trabalho.
Fico feliz por ter ajudado o protagonista de jaleco branco. Meus conselhos sobre roleta se limitam a jogos na Terra; suborno é recomendado no seu planeta.
Joguei o mesmo número 1000 vezes seguidas em uma roleta com o número 0,00 e acertei 6 vezes. Qual a probabilidade de acertar 6 vezes ou menos nesse cenário?
A probabilidade de seu número aparecer exatamente x vezes é combin(1000,x)*(1/38) x *(37/38) 1000-x . A tabela a seguir mostra a probabilidade de todos os números de acertos de 0 a 6 e o total.
Vitórias em 1000 apostas na roleta
| Número | Probabilidade |
| 0 | 0,00000000000262 |
| 1 | 0,00000000007078 |
| 2 | 0,00000000095556 |
| 3 | 0,00000000859146 |
| 4 | 0,00000005787627 |
| 5 | 0,00000031159330 |
| 6 | 0,00000139655555 |
| Total | 0,00000177564555 |
Portanto, a resposta é 0,00000177564555, ou 1 em 563175. Espero que isso não tenha acontecido em um cassino online.
Você pode estar se perguntando por que eu não usei a aproximação normal, como fiz no problema do lançamento de moeda acima. Isso ocorre porque ela não funciona bem com probabilidades muito altas ou muito baixas.
Oi Mike, só para descontrair um pouco, lembro de ter visto você jogar roleta em um episódio especial do Vegas Challenge há um tempo. Obviamente, você sabia que seu valor esperado não mudaria, independentemente da estratégia. Lembro de você jogar apenas com um número, mas esqueci se você mudava de número depois de ganhar. Não sei o que eu faria na sua situação, mas por curiosidade, você jogou com um único número em vez de uma aposta externa, como vermelho/preto, para maximizar a variância? Assim, se você tiver "sorte", estará com a maior vantagem possível? Enfim, gostei do fato de você ter jogado com uma estratégia bem conservadora e sem graça.
Você analisou minha estratégia muito bem. Eu pretendia apostar o mínimo durante a maior parte do programa para evitar que a vantagem da casa me prejudicasse. O produtor não gostou de uma estratégia tão monótona, então tentei parecer mais animado do que normalmente seria. O motivo de eu ter escolhido um único número em vez de uma aposta com probabilidades iguais foi a volatilidade. Eu sabia que se terminasse perto do meu ponto inicial de US$ 10.000, provavelmente perderia. Então, queria uma chance maior de sair na frente. Mantive a aposta no 23 o tempo todo, embora tenha adicionado o 5 no final. Fico feliz que tenha gostado do programa.
Minha pergunta se baseia mais em observações suas e em boatos que ouvi. Se é verdade que os crupiês de Las Vegas, quando treinados na escola de crupiês, aprendem a girar e lançar a bola da mesma maneira, então é verdade que, observando como um crupiê gira a roleta, é possível determinar o quadrante da roleta em que a bola pode parar?
Não. Os crupiês aprendem apenas o básico e nada que se aproxime dessa habilidade. Aliás, se um crupiê tivesse esse controle, ele poderia simplesmente pedir a um cúmplice que apostasse onde ele planejasse que a bola caísse e eles poderiam facilmente ganhar milhões.
Qual a probabilidade de jogar 15 rodadas na roleta europeia, cobrindo oito números, e não acertar nenhum?
A probabilidade de perder uma rodada é 1-(8/37) = 78,38%. Portanto, a probabilidade de perder 15 rodadas é 0,7838 15 = 2,59%.
Gostaria de saber como testar um jogo de roleta online, para conhecer as probabilidades e se elas são honestas?
Primeiramente, deixe-me explicar como NÃO testar um jogo. Você não deve gravar todas as suas jogadas e, ao terminar, procurar por qualquer anomalia para depois me escrever reclamando que o cassino está trapaceando. O jeito correto é formular uma hipótese sobre como o cassino está trapaceando PRIMEIRO, depois coletar dados e, finalmente, verificar se os dados confirmam sua hipótese. Se você não sabe que tipo de hipótese formular, sugiro simplesmente testar o número de vitórias e derrotas e apostar sempre a mesma coisa. Se você executar os dois primeiros passos corretamente e precisar de ajuda com o terceiro, fique à vontade para me escrever.
Quando entro num cassino com US$ 100 e jogo roleta, não espero sair com 4% a menos, mas sim com 25% a menos. Esse fenômeno tem um nome formal? (Pesquisei no Google por "vantagem real da casa"). Existe alguma fórmula ou modelo para prever essa "vantagem real da casa"? Quais jogos são melhores e quais são piores nesse quesito?
No seu exemplo, a margem de lucro do cassino é de 75%. Essa é a proporção entre o valor das fichas que os jogadores levam para casa e a quantia de dinheiro que o crupiê coloca na caixa. Embora existam médias históricas, não há como converter a vantagem da casa em lucro. O lucro depende, em parte, de quanto tempo o jogador vai usar suas fichas, e não há como saber isso.
Se eu tiver uma banca de $200 que não me importo de perder, e continuar apostando $10 em um único número na roleta europeia (com um único zero), quais são as probabilidades de ganhar $200, $500 ou $1000? Supondo que eu pare depois de atingir a meta. Obrigado, ótimo site, você queria que eu fosse breve :)
Obrigado pelo elogio. Existe uma fórmula para questões como essa, que explico no meu site www.mathproblems.info , veja o problema 116.
Com uma banca de b unidades, um objetivo de ganho de g unidades, probabilidade de ganhar p e probabilidade de perder q, sua probabilidade de sucesso é ((q/p) b -1)/((q/p) b+g -1). Neste caso, b=20, p=18/37, q=19/37 e g=20, 50 e 100. Portanto, para uma banca de $200, a probabilidade é ((19/18) 20 -1)/((19/18) 40 -1) = 0,253252.
Para um gol vencedor de $500 a probabilidade é ((19/18) 20 -1)/((19/18) 70 -1) = 0,045293.
Para um gol vencedor de $1.000, a probabilidade é ((19/18) 20 -1)/((19/18) 120 -1) = 0,002969.
Numa roleta de 38 números... depois de sair três vermelhos, um verde e outro vermelho... qual a probabilidade de, nas próximas três rodadas consecutivas, sair o vermelho 23?
Não faz diferença quais foram as rodadas anteriores. A probabilidade de sair vermelho 23 três vezes seguidas é (1/38) 3 = 1 em 1 em 54.872.
Visitei o site da Bodog e experimentei a roleta deles na versão gratuita. Em um quadro no canto superior, são registrados os últimos dez números que saíram. Tenho certeza de que girei a roleta menos de 20 vezes. Os números registrados foram os seguintes: 9-9-29-21-11-11-20-28-32-1. Curiosamente, duas rodadas antes disso, o número 32 saiu novamente. Isso significa que os números 9, 11 e 32 saíram duas vezes em apenas 12 rodadas. Como eu disse, não sou estatístico, mas a frequência desses três números, juntamente com o número mínimo de vezes que girei a roleta, parece indicar que algo está errado.
A probabilidade de três pares e seis singletons em doze spins é combin (38,3) × combin(35,6) × combin(12,2) × combin(10,2) × combin(8,2) × fact(6)/38 12 = 9,04%. Os cálculos ficam um pouco complicados ao considerarmos a probabilidade de isso acontecer em qualquer intervalo de 12 spins em um total de 20 spins. Basta dizer que é significativamente maior que 9%, mais provável do que improvável, eu diria. Portanto, esses resultados me parecem bastante normais.
Um dos cassinos da minha cidade está pagando 36 para 1 para uma aposta direta em uma roleta com um único zero, em um número específico para aquele dia. Por exemplo, o número específico é 8 no dia 8 do mês. Como isso altera a vantagem da casa? Obrigado pela ajuda.
A vantagem da casa no número especificado seria exatamente 0%.
O cassino Orleans oferece uma aposta paralela na roleta que paga 8 para 1 em três vermelhos (ou pretos) em sequência. Ela está localizada em uma roleta com duplo zero. Você poderia me informar as probabilidades?
A probabilidade de ganhar é (18/38) 3 = 10,63%. A vantagem da casa é 8×0,1063 - 1×0,8937 = 4,34%, que é menor que os 5,26% em todas as outras apostas (exceto a temida combinação 0,00,1,2,3 com 7,89%).
Em alguns cassinos na Holanda, é permitido o triplo aprisionamento na roleta. Qual é a vantagem da casa para apostas com probabilidades iguais sob essa regra? Estou mais interessado na solução do que na resposta.
Para benefício de outros leitores, em muitos cassinos na Europa, se você fizer uma aposta de probabilidade igual na roleta e a bola cair no zero, a aposta fica "presa". Se a próxima jogada resultar em uma vitória, a aposta é devolvida sem ganhos. Se a bola cair no lado oposto, a aposta é perdida.
O que acontece com apostas de prisão simples se a bola cair no zero? Se o cassino permitir apenas prisão simples, a aposta será perdida. No entanto, alguns cassinos permitem prisão dupla, que é o que aconteceria. Se uma aposta com prisão dupla for vencedora, ela volta a ser de prisão simples. Se o cassino permitir apenas até prisão dupla, uma aposta com prisão dupla perderia se caísse outro zero. Pela mesma lógica, se um cassino permitir prisão tripla, uma aposta com prisão dupla se tornaria prisão tripla se caísse outro zero.
A vantagem da casa no aprisionamento triplo é de 1,370120%. Antes de explicar como cheguei a esse resultado, vamos analisar primeiro o aprisionamento simples e o duplo. Suponha que a primeira aposta seja no vermelho.
Seja Z = probabilidade de zero = 1/37.
Seja R = probabilidade de um número vermelho = 18/37.
prisão individual
pr(push) = ZR = 0,0131482834.
pr(win) = R = 0,4864864865.
pr(perda) = 1-pr(push)-pr(vitória) = 0,5003652301.
Valor esperado = pr(vitória)-pr(derrota) = -0,0138787436.
Dupla prisão
O jogador empurra se a primeira rodada for zero, podendo então repetir ZR de 0 até um número infinito de vezes, até obter um vermelho. Em outras palavras, as maneiras de empurrar são:
ZR, Z(ZR)R, Z(ZR)(ZR)R, Z(ZR)(ZR)(ZR)R, ...
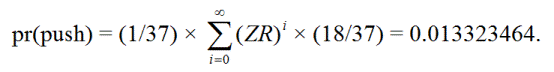
pr(push) = 0,013323464
pr(win) = 18/37 = 0,4864864865.
pr(perda) = 1-pr(push)-pr(vitória) = 0,5001900494.
Valor esperado = pr(vitória)-pr(derrota) = -0,0137035629.
Tripla prisão
Primeiro, vamos encontrar a probabilidade p 1 de que uma aposta inicialmente "aprisionada" se torne triplamente "aprisionada" com mais dois zeros e, eventualmente, volte a ser uma aposta individual aprisionada. Isso pode acontecer da seguinte forma:
ZZRR, ZZ(RZ)RR, ZZ(RZ)(RZ)RR, ZZ(RZ)(RZ)(RZ)RR, ...
Em outras palavras, a aposta pode oscilar entre prisão tripla e dupla um número infinito de vezes.
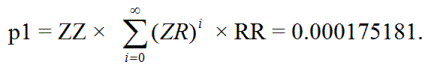
Em segundo lugar, seja p 2 = a probabilidade de uma aposta com prisão simples atingir o primeiro ou segundo nível de prisão e depois retornar à prisão simples.
seja p 2 = ZR + p 1 = 0,013323464.
O jogador pode repetir o processo de retornar ao primeiro nível, partindo de zero, um número infinito de vezes. Portanto, a probabilidade de um empurrão é:
ZR + Z p 2 R + Z p 2 p 2 R + Z p 2 p 2 p 2 R + ... =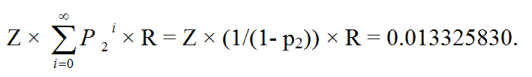
Z × (1/(1- p 2 )) × R = 0,013325830.
pr(push) = 0,013325830.
pr(win) = 18/37 = 0,4864864865.
pr(perda) = 1-pr(push)-pr(vitória) = 0,5001876839.
Valor esperado = pr(vitória)-pr(derrota) = -0,0137011974.
Prisão infinita
Não que você tenha perguntado, Maff, mas ouvi dizer que na Espanha permitem prisão perpétua. Seja p a probabilidade de um empurrão. Essa também é a probabilidade de começar no nível x de prisão, cair em níveis cada vez mais baixos, mas eventualmente voltar a subir para x.
p = ZR + ZpR + ZppR + ZpppR + ...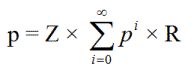
p 2 - p + ZR = 0
Pela fórmula quadrática p = (1-(1-4*RZ) 1/2 )/2 = 0,0133258620.
pr(push) = 0,0133258620.
pr(win) = 18/37 = 0,4864864865.
pr(perda) = 1-pr(push)-pr(vitória) = 0,5001876515.
Valor esperado = pr(vitória)-pr(derrota) = -0,0137011650.
Zeros ignoraram a prisão
Finalmente, em alguns cassinos, os zeros são simplesmente ignorados após o primeiro zero que prende a aposta. Nesses casos, a probabilidade de um empate é simplesmente (1/37)×(1/2) = 0,0135135135.
A tabela a seguir resume os quatro tipos de regras.
Probabilidades de prisão
| Prisão | Ganhar | Empurrar | Perda | Esperado Valor |
| Solteiro | 0,48648649 | 0,01314828 | 0,50036523 | -0,01387874 |
| Dobro | 0,48648649 | 0,01332346 | 0,50019005 | -0,01370356 |
| Triplo | 0,48648649 | 0,01332583 | 0,50018768 | -0,01370120 |
| Infinito | 0,48648649 | 0,01332586 | 0,50018765 | -0,01370117 |
| Zeros ignorados | 0,48648649 | 0.01351351 | 0,50000000 | -0,01351351 |
Gostaria de agradecer a ChesterDog e weaselman pela ajuda matemática. Gostaria também de agradecer e mencionar o professor G. Artico e o site polarprof.it pelo código HTML da fórmula de somatório acima.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Existe algum padrão na ordem dos números na roleta?


A ideia é que a roda esteja equilibrada. Em outras palavras, se você calcular a média de uma seção de números consecutivos na roda, ela estará próxima da média de 18,5. Pensei em uma maneira de explicar como os números são distribuídos em uma roda com duplo zero, da seguinte forma.
- Posicione o 00 na posição das 12:00 e o 0 na posição das 6:00.
- Os números na parte superior da roda são 13, 1, 00, 27, 10*, 25. Isso deve ser simplesmente memorizado.
- Todos os números ímpares baixos (de 1 a 17) estão do lado esquerdo e os números ímpares altos (de 19 a 35) do lado direito.
- Começando com o 1 e o 13, mova-se quatro posições no sentido anti-horário para obter o próximo número ímpar, mas não ultrapasse o zero.
- Como exceção à regra 4, não coloque o 19 quatro posições no sentido anti-horário a partir do 17, pois o 19 é um ímpar alto e pertence ao lado direito. Em vez disso, coloque o 11, o único ímpar baixo que não está contemplado na regra 4.
- Todos os números pares estão diretamente opostos no círculo, a 180 graus, em relação ao número ímpar anterior.
Não sei explicar a ordem em uma roda de zero único. Por enquanto, posso dizer que se você colocar o zero na posição das 12 horas, então:
- Do lado esquerdo estarão todos os números baixos em vermelho e os números altos em preto.
- Do lado direito estarão todos os números altos em vermelho e os números baixos em preto.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
Eu registrei 3.000 giros na roleta de duplo zero porque os primeiros doze números não pareciam sair com tanta frequência quanto os dois últimos. Nesses 3.000 giros, os números de 1 a 12 saíram 742 vezes. Qual a probabilidade disso?
Você esperaria que o número de vezes que a bola cairia de 1 a 12 fosse 3000*(12/38) = 947,37.
A diferença entre seus resultados e as expectativas é de 947,37 - 742 = 205,37.
A variância é 3000*(12/38)*(1-(12/38)) = 648,20.
O desvio padrão é a raiz quadrada da variância = sqrt(648,20) = 25,46.
Seus resultados estão 205,37/25,46 = 11,75 desvios padrão abaixo do esperado.
O valor p, ou a probabilidade de estar errado por 11,75 desvios padrão ou mais, é de 1 em 28.542.806.257.940.300.000.000.000.000.000.
Gostaria de saber onde está a roda.
Qual a sua opinião sobre a estratégia de roleta Comp Killer, conforme abordada neste vídeo ?
É fácil perceber que o objetivo desse sistema é cobrir a maioria dos números, sendo assim uma forma de jogar roleta com risco relativamente baixo. Veja quanto apostar em cada rodada:
- US$ 5 cada nos números 3, 16, 24, 28 e 33.
- Faça uma aposta de canto em cada um destes conjuntos de números: 2/3/5/6, 7/8/10/11, 14/15/17/18, 19/20/22/23, 26/27/29/30, 31/32/34/35.
Note que isso não inclui os seguintes nove números: 0, 00, 4, 9, 12, 13, 21, 25 e 36.
A tabela de retorno a seguir mostra a probabilidade e a contribuição para o retorno de todos os resultados possíveis.
Assassino de Competição
| Evento | Lucro líquido | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| Vitória incontestável | 5 | 5 | 0,131579 | 0,657895 |
| Vitória no escanteio | 50 | 24 | 0,631579 | 31,578947 |
| Todos os outros | -175 | 9 | 0,236842 | -41,447368 |
| Total | 38 | 1.000000 | -9,210526 |
A célula inferior direita mostra uma perda esperada de $9,21 por rodada. O valor total apostado por rodada é de $175. Isso resulta em uma vantagem da casa de $9,21/$175 = 5,26%, a vantagem da casa na roleta com duplo zero.
Gostaria de acrescentar que você provavelmente perderá mais em créditos do que receberá de volta com essa estratégia, ou com qualquer outra estratégia de roleta. A regra geral é que os cassinos devolvem cerca de 1/3 da sua perda esperada em créditos. Existem maneiras de enganar os cassinos, fazendo-os acreditar que sua perda esperada é maior do que realmente é, mas jogar com essa estratégia não é uma delas.
O que você acha dessa estratégia na roleta?
- Aposte duas unidades no preto.
- Aposte uma unidade na terceira coluna.
A beleza dessa estratégia reside no fato de haver 8 números vermelhos e 4 números pretos na terceira coluna. Dos 16 números vermelhos, metade está nas colunas 1 ou 2 e a outra metade na coluna 3. Vamos ignorar o 0 e o 00 por enquanto. Quando a bola cai no vermelho, 8 dos 18 números vermelhos estão na terceira coluna. Se a probabilidade de ganhar é de 8/18 e os ganhos pagam 2 para 1, tenho uma vantagem de 33,3%. Mesmo se fizermos a média com a aposta no preto, que tem 0% de vantagem da casa, e ignorando novamente o 0 e o 00 por enquanto, ainda tenho uma vantagem de 16,7%. Incluindo o 0 e o 00, minha vantagem não seria (2/38)*-100% + (36/38)*16,7% = 10,53%? O que você acha?
Concordo que a vantagem condicional da aposta na terceira coluna é de 33,3%, assumindo que a bola caia no vermelho e ignorando os dois zeros. No entanto, pela mesma lógica, se a bola cair no preto, a probabilidade de a aposta na terceira coluna ganhar é de 4/18 = 2/9. Uma aposta com 2/9 de chance de ganhar que paga 2 para 1 teria uma vantagem da casa de 33,33%. Portanto, considerando sua perspectiva, a aposta na terceira coluna teria uma vantagem do jogador de 33,33% metade das vezes e uma vantagem da casa de 33,33% na outra metade. Cancelando-se mutuamente, essa aposta tem 0% de vantagem da casa. Finalmente, considerando os dois zeros, a vantagem total do jogador é de (2/38)*-100% + (36/38)*0% = -5,26%.
Analisando de outra forma, a tabela a seguir mostra o número de maneiras pelas quais todos os resultados possíveis podem ocorrer, a probabilidade, as unidades ganhas e a contribuição para o retorno. A célula inferior direita mostra uma perda esperada de -0,105263 unidades. Dividindo isso pelas duas unidades apostadas, chega-se a uma vantagem da casa de 5,26%.
Estratégia da Boêmia
| Evento | Paga | Números | Probabilidade | Retornar |
|---|---|---|---|---|
| 0, 00 | -2 | 2 | 0,052632 | -0,105263 |
| Vermelho e coluna 1 ou 2 | -2 | 10 | 0,263158 | -0,526316 |
| Vermelho e coluna 3 | 1 | 8 | 0,210526 | 0,210526 |
| Preto e coluna 1 ou 2 | 0 | 14 | 0,368421 | 0,000000 |
| Preto e coluna 3 | 3 | 4 | 0,105263 | 0,315789 |
| Total | 38 | 1.000000 | -0,105263 |
Qual é o número esperado de rodadas necessárias para obter cinco vermelhas ou cinco pretas em sequência?
Aqui está minha solução (PDF).
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Ouvi dizer que já existe roleta com quatro zeros. Qual é a vantagem da casa?

Sim, esse tipo de roda é comercializado pela TCS John Huxley . Ainda não tenho conhecimento de nenhuma propaganda em andamento.
A fórmula para a vantagem da casa na roleta padrão é z/(36+z), onde z = número de zeros. Neste caso, a vantagem da casa é 4/(36+4) = 4/40 = 1/10 = 10%.


