Vídeo pôquer - Perguntas gerais
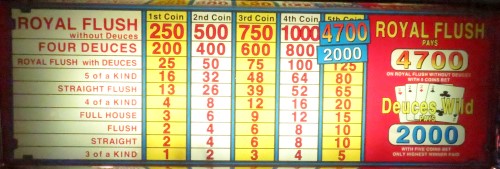
Estou jogando em uma máquina caça-níqueis com bônus 8/5 que paga $1.199 por um Royal Flush e o dobro por uma quadra de 8, além dos bônus normais para quadras de 2, 3, 4 e ases. Meu cartão de fidelidade e o número máximo de moedas são necessários. Isso garante um retorno de 100% ou mais?
O prêmio de US$ 1199 é curioso, ficando um pouco abaixo do limite de US$ 1200 para o qual o cassino seria obrigado a declarar o ganho ao IRS (Receita Federal dos EUA). O software Winpoker 6 permite a análise de jogos personalizados. Neste caso, o retorno é de 100,0079%.
Um jogo de video poker, seja Jacks or Better ou qualquer outra versão com curingas, funciona como um jogo de cartas real? Em outras palavras, a tabela de pagamentos na frente da máquina determina o retorno exato que ela oferece, ou isso pode ser alterado internamente com chips de computador, tornando a tabela de pagamentos irrelevante? Sempre achei que isso seria desonesto até ler um artigo na revista Strictly Slots que afirmava que isso já foi feito e é possível. Se isso for verdade, poderíamos ter duas máquinas de video poker idênticas lado a lado com vantagens da casa diferentes, como acontece em cassinos e máquinas caça-níqueis comuns. Se for assim, então toda essa porcentagem de retorno em tabelas de pagamentos de video poker que venho lendo há anos em revistas, softwares e livros se torna inútil.
Tenho plena confiança de que qualquer fabricante respeitável de máquinas de videopôquer as produz de forma justa e precisa. É possível que existam máquinas ou fichas desonestas por aí? Claro que sim. Gostaria de ler o artigo a que você se refere.
Estou pensando em visitar os sites dos seus anunciantes só para garantir que eles continuem apoiando seu site, que oferece dicas gratuitas para o público que gosta de jogos de azar. Seu site é ótimo. Minha pergunta é: é possível comprar a mesma carta descartada no videopôquer? O Conselho de Controle de Jogos de Michigan me deu uma resposta incompleta, afirmando que todos os eventos são determinados por um gerador de números aleatórios. Em segundo lugar, as chances de conseguir mãos vencedoras no videopôquer estão sujeitas à manipulação do cassino, como acontece nas máquinas caça-níqueis, que também são regidas por um gerador de números aleatórios?
Obrigado pelo seu apoio. Encorajo todos a clicarem nos banners para ajudar a apoiar o site. Respondendo à sua pergunta, não, não é possível receber a mesma carta de volta. A máquina representa uma distribuição justa de um único baralho. Uma vez descartada uma carta, você não pode recuperá-la. Respondendo à segunda pergunta, não, o cassino não pode alterar a probabilidade de cada mão. As máquinas de videopôquer oferecem um jogo justo. A frequência com que você recebe cada mão depende do sorteio aleatório das cartas e da sua habilidade no jogo.
No Mississippi, a lei para o video poker é a mesma que em Nevada, ou seja, cada mão é considerada um novo jogo?
Suponho que você esteja perguntando se cada mão é distribuída a partir de um baralho novo, sem memória das mãos anteriores. É assim que o vídeo pôquer deve ser jogado e tenho certeza de que no Mississippi não é diferente.
Sua coluna no jornal online não é atualizada desde junho. Está tudo bem? Espero que sim. Tenho um guia básico de estratégia para Blackjack e ele é muito útil. Existem guias básicos de estratégia para jogos de pôquer eletrônico? Obrigado pela atenção.
Não tenho certeza a qual coluna de jornal online você se refere. Mas tudo bem. Aliás, você pode encontrar minhas estratégias de videopôquer em um prático cartão de estratégias na Custom Strategy Cards. Os cartões de videopôquer podem ainda não estar listados, mas sei que o proprietário os tem, então é só perguntar.
Atualização: O serviço de Cartões de Estratégia Personalizados não existe mais.
Prezado Sr. Wizard, como as leis de retorno mínimo afetam as máquinas de videopôquer? Um cassino pode instalar uma máquina de videopôquer se não conhecer a estratégia ideal? Jogadores realmente imprudentes (aqueles que descartariam um par ou até mesmo um royal flush) podem processar um cassino se sua estratégia resultar em pagamentos abaixo de x%, conforme exigido pela lei estadual? Por fim, por curiosidade, qual é o retorno mínimo possível em uma máquina de videopôquer, considerando o descarte de um royal flush, a manutenção das 5 cartas de uma mão ruim, etc.? Agradeço seu valioso tempo e espero que possa responder.
A regulamentação 14.040.1(a) do Conselho de Controle de Jogos de Nevada estabelece que os dispositivos de jogo devem retornar pelo menos 75%, assumindo uma estratégia ideal do jogador. Para responder à sua segunda pergunta, modifiquei meu programa de vídeo pôquer para sempre fazer a pior jogada possível. Por exemplo, manter todas as cinco cartas em uma mão sem pagamento e descartar parte ou todas as mãos iniciais. Com base no Jacks or Better 9/6, essa estratégia resulta em um retorno de 2,72%, ou uma vantagem da casa de 97,28%. A seguir, está a tabela completa de retorno. Um jogador assim não poderia processar o cassino, pois a culpa seria dele por jogar tão mal.
Jacks or Better - Pior Jogador Possível
| Mão | Pague | Número | Probabilidade | Retornar |
|---|---|---|---|---|
| Rubor Real | 800 | 48564 | 0,000000 | 0,000002 |
| Straight flush | 50 | 2058000 | 0,000000 | 0,000005 |
| 4 de um tipo | 25 | 38040380 | 0,000002 | 0,000048 |
| Casa cheia | 9 | 292922028 | 0,000015 | 0,000132 |
| Descarga | 6 | 336550092 | 0,000017 | 0,000101 |
| Direto | 4 | 6239759724 | 0,000313 | 0,001252 |
| 3 de um tipo | 3 | 12510891616 | 0,000628 | 0,001883 |
| Dois pares | 2 | 34968642984 | 0,001754 | 0,003509 |
| Valetes ou melhor | 1 | 334574728656 | 0,016785 | 0,016785 |
| Nada | 0 | 19544266875156 | 0,980487 | 0,000000 |
| Total | 19933230517200 | 1.000000 | 0,023717 |
Se você tivesse que escolher um jogo de video poker para praticar online (para saber como jogar quando estiver em Las Vegas), qual seria?
Tudo o que você precisa está aqui!
Existe um jogo de vídeo pôquer para você jogar, que irá corrigi-lo quando você cometer erros.
Tenho um analisador de mãos que permite analisar como jogar qualquer mão.
Apresento aqui minha calculadora de retorno de jogos para determinar o retorno de qualquer jogo e tabela de pagamentos.
Por fim, tenho o meu criador de estratégias , que permite criar uma estratégia para qualquer jogo.
Nota: Esta resposta foi atualizada em 13 de novembro de 2013.
Se eu colocar uma nota de 100 dólares em uma máquina de videopôquer com retorno de 98% e jogar até perder tudo, quanto eu apostarei em média no total?
Existe uma fórmula simples para essa resposta. É o investimento inicial dividido pela vantagem da casa. Nesse caso, a resposta é $100/0,02 = $5000. No entanto, devido à volatilidade do videopôquer, na maioria das vezes os $100 não durarão tanto tempo.
Alguma dica para nós, moradores de Connecticut, que temos as piores máquinas de videopôquer do mundo? Existe alguma maneira aceitável de pressionar um cassino a melhorar sua seleção quando o mercado não exige isso?
É isso que acontece em um ambiente com quase nenhuma concorrência. Pedir ao cassino máquinas melhores não vai adiantar. Se os jogadores vão jogar jogos com tabelas de pagamento ruins, por que eles deveriam mudar alguma coisa? Sua única esperança é escrever para os legisladores de Connecticut e pedir que acabem com o monopólio de dois cassinos no setor de jogos de azar naquele estado e permitam que outros concorram.
Se você estivesse jogando com uma aposta de $50 por partida, qual escolheria entre estes dois jogos de vídeo pôquer (considerando que ambos os jogos têm as mesmas tabelas de pagamento e que você aposta o máximo de 5 moedas por mão): uma partida simples com aposta de $10 ou dez partidas com aposta de $1 por mão? Agradeço sua atenção e consideração.
Matematicamente, é claro que ambos têm o mesmo retorno esperado. No entanto, eu jogaria na opção de 10 rodadas porque a volatilidade é menor e acho que é mais divertido.
Existem muitos jogos de vídeo pôquer online gratuitos disponíveis. No entanto, estou procurando uma versão que eu possa executar sem estar conectado à internet. Você conhece alguma versão gratuita para download do Jacks or Better que não utilize a internet enquanto estiver em execução? Encontrei algumas demos gratuitas para download, mas elas ainda se conectam a um site ao serem executadas, mesmo que o jogo esteja sendo carregado localmente. Uma versão básica, realista (em termos de funcionalidade) seria ótima. Obrigado.
Acredito que a versão demo gratuita do Winpoker fará isso e nunca expirará. O download está disponível em www.zamzone.com .
Qual é o coeficiente de assimetria para o video poker?
Para benefício de outros leitores, o coeficiente de assimetria (ou assimetria) de qualquer variável aleatória é uma medida de qual direção possui a cauda mais longa. Uma assimetria negativa significa que os resultados mais prováveis estão no lado superior da distribuição, compensados pelos extremos que tendem a estar no lado inferior. Uma assimetria positiva é o oposto, onde os resultados mais prováveis estão no lado inferior, mas com os extremos tendendo a estar no lado superior. A média é menor que a mediana com uma assimetria negativa e maior com uma assimetria positiva. Uma fórmula exata pode ser encontrada na Wikipédia ou em diversos livros de estatística.
Em termos gerais, a assimetria está relacionada à frequência com que você ganha em uma sessão. Em Jacks or Better, na maioria das vezes, você não terá uma sessão vencedora em algumas horas se não conseguir um Royal Flush. Já no Double Double Bonus, você pode ganhar com mais frequência depois de algumas horas devido aos grandes pagamentos de quadra. Como a maioria das pessoas está sujeita a vieses cognitivos, a dor de uma perda é duas vezes maior que o prazer de uma vitória. As pessoas não jogam Double Double Bonus porque gostam da variância, mas sim porque têm uma chance maior de ganhar. A tabela a seguir mostra algumas estatísticas importantes para quatro jogos de vídeo pôquer comuns. É interessante notar que a assimetria é maior em Jacks or Better.
Estatísticas principais do vídeo poker
| Estatística | Trabalho — 9/6 | BP — 8/5 | DDB — 9/6 | DW — NSUD |
|---|---|---|---|---|
| Retornar | 0,995439 | 0,99166 | 0,989808 | 0,997283 |
| Variância | 19,514676 | 20.904113 | 41,985037 | 25,780267 |
| Inclinar | 147,114643 | 134,412152 | 66,495372 | 101,23991 |
| (Excesso) Curtose | 26.498 | 23.202 | 6.679 | 14.550 |
Vaga — 9/6 = Salário integral ou melhor
BP — 8/5 = Bônus de pagamento padrão no Poker
DDB — 9/6 = Pagamento padrão Double Double Bonus Poker
DW — NSUD = "Not so Ugly Ducks" Deuces Wild
Como saber isso pode realmente ajudar o jogador de vídeo pôquer? Suponho que se possa dizer que um jogo com uma grande assimetria tem uma probabilidade maior de resultar em perda ao longo de uma sessão de algumas horas. Por exemplo, em Jacks or Better, se você não conseguir nenhuma combinação Royal Flush, a vantagem da casa provavelmente acabará corroendo seu saldo. No entanto, em um jogo como Deuces Wild ou Double Double Bonus, as segundas maiores vitórias podem te tirar do prejuízo ao longo de uma sessão. Em outras palavras, a assimetria impede que você ganhe quando não consegue combinações Royal Flush. Conhecer a assimetria não aumentará suas chances de ganhar, mas é mentalmente útil saber o que esperar. Então, da próxima vez que você perder no Jacks or Better 9/6, atribua isso à assimetria.
Meus agradecimentos a Jeff B. pela ajuda com esta questão.
Eu estava jogando video poker em Atlantic City e juraria que, às vezes, recebia a mesma carta que havia descartado. Se a máquina estivesse colocando as cartas descartadas de volta no baralho, qual seria o efeito nas probabilidades?
Os cassinos online da Cryptologic têm um jogo chamado Bonus Video Poker , onde as cartas descartadas são devolvidas ao baralho. A tabela de pagamento 40-20-9-6 do Jacks or Better nesse jogo retorna 95,2642%, antes de considerar o recurso de bônus de recompra, que não abordarei aqui. No vídeo pôquer convencional, essa tabela de pagamento retornaria 98,2534%. Portanto, neste exemplo, devolver as cartas descartadas ao baralho custa ao jogador quase 3%. No entanto, duvido muito que isso realmente tenha acontecido em uma máquina em Atlantic City.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Qual jogo de vídeo poker oferece a melhor chance de conseguir um royal flush?
Vamos começar analisando alguns jogos de vídeo pôquer simples e diretos. A tabela a seguir mostra a probabilidade de um Royal Flush, da maior para a menor. Esta tabela não inclui os Royal Flush com Wild, que pagam muito menos que um Royal Flush natural.
Probabilidade do Vídeo Poker Royal
| Jogo | Probabilidade | Inverso |
|---|---|---|
| 17-7 Joker Poker | 0,0000259892 | 38.478 |
| Bônus de pôquer 8-5 | 0,0000248551 | 40.233 |
| 9-6 Jacks | 0,0000247583 | 40.391 |
| 9-6 Bônus Duplo Duplo | 0,0000245102 | 40.799 |
| 9-6 Bonus Poker Deluxe | 0,0000237661 | 42.077 |
| "Pagamento integral" deuces wild | 0,0000220839 | 45.282 |
| 10-7 Bônus Duplo | 0,0000208125 | 48.048 |
Surpreendentemente, o Joker Poker é o que tem maior probabilidade de formar um Royal Flush natural. Isso me surpreende por causa da carta extra, que não pode ser usada para formar um Royal Flush natural.
A seguir, vamos analisar alguns jogos de video poker não convencionais.
No Jacks Royal Draw 9-6, as probabilidades são de 1 em 12.178.
Na aposta 7-5 Jacks Second Chance Royal , as probabilidades são de 1 em 10.827. Isso inclui as apostas "second chance royal", que pagam apenas 200.
Por fim, acho que uma menção honrosa deve ser feita ao Triple Double Bonus, onde quatro ases mais um kicker 2-4 pagam os mesmos 800 por moeda apostada que um royal flush. As chances de ganhar 800 são de 1 em 10.823, com base na tabela de pagamento 9-7. Ainda melhor é o Royal Aces Bonus Poker , que paga 800 por qualquer royal flush ou quatro ases, resultando em uma probabilidade de 1 em 3.673 de ganhar 800.
No entanto, considerando todos os fatores, minha resposta para o jogo com o maior número de sequências reais naturais é Chase the Royal . Com base na tabela de pagamento de Valetes de 9 a 6, a probabilidade de um royal flush é de 1 em 9.084.
Por que o número 19.933.230.517.200 aparece com tanta frequência como o total de combinações no vídeo pôquer?
Para benefício de outros leitores, segue a tabela de retorno para o jogo 9-6 Jacks or Better.
"9-6" Jacks ou Melhor
| Mão | Pague | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| Rubor Real | 800 | 493512264 | 0,00002476 | 0,01980661 |
| Straight flush | 50 | 2178883296 | 0,00010931 | 0,00546545 |
| Quatro de um mesmo tipo | 25 | 47093167764 | 0,00236255 | 0,05906364 |
| Casa cheia | 9 | 229475482596 | 0,01151221 | 0,10360987 |
| Descarga | 6 | 219554786160 | 0,01101451 | 0,06608707 |
| Direto | 4 | 223837565784 | 0,01122937 | 0,04491747 |
| Três de um tipo | 3 | 1484003070324 | 0,07444870 | 0,22334610 |
| Dois pares | 2 | 2576946164148 | 0,12927890 | 0,25855780 |
| Valetes ou Melhor | 1 | 4277372890968 | 0,21458503 | 0,21458503 |
| Nada | 0 | 10872274993896 | 0,54543467 | 0 |
| Total | 19933230517200 | 1 | 0,99543904 |
A maioria das minhas tabelas de retorno de video poker para jogos de 52 cartas tem o mesmo número de combinações: 19933230517200. A questão é: por quê?
Primeiro, existem combin (52,5) = 2.598.960 maneiras de escolher cinco cartas dentre 52.
Em segundo lugar, existem até combin(47,5) = 1.533.939 combinações no descarte, dependendo de quantas cartas o jogador descarta. A tabela a seguir mostra o número de combinações de descarte na segunda coluna de acordo com o número de descartes.
Combinações de sorteio
| Descartar | Combinações | Peso | Produto |
|---|---|---|---|
| 0 | 1 | 7.669.695 | 7.669.695 |
| 1 | 47 | 163.185 | 7.669.695 |
| 2 | 1.081 | 7.095 | 7.669.695 |
| 3 | 16.215 | 473 | 7.669.695 |
| 4 | 178.365 | 43 | 7.669.695 |
| 5 | 1.533.939 | 5 | 7.669.695 |
O mínimo múltiplo comum dos números na segunda coluna é 7.669.695. Esse número pode ser expresso como 5×combin(47,5). Para manter o número total de combinações o mesmo para cada mão na distribuição, pondero as combinações de descarte de forma que o total de combinações no descarte seja 7.669.695.
Portanto, 19.933.230.517.200 = combin(52,5)×combin(47,5)×5. Algumas das minhas mesas de video poker de 52 cartas têm um número menor de combinações. Isso ocorre porque, às vezes, o número total de combinações para cada mão na tabela de retorno final tem um maior divisor comum maior que um. Nesse caso, às vezes divido cada total pelo maior divisor comum. Meu analisador de video poker faz isso automaticamente.
Essa questão foi levantada e discutida no meu fórum Wizard of Vegas .
É verdade que o cassino D removeu o jogo Loose Deuces de 101,60%? Lembro-me de você ter dito que essa era a máquina de videopôquer mais generosa de Las Vegas. Se os rumores forem verdadeiros, qual é a máquina número um agora?
Sim, essa máquina não existe mais. Como você apontou, o jogo que antes era o segundo colocado agora ocupa o primeiro lugar. É um jogo Double Deuces com 100,92% de retorno no El Cortez. A tabela de pagamento completa é 940-400-25-16-13-4-3-2-2-1. Ela fica na sala de caça-níqueis na extremidade norte do cassino, que é cheia de máquinas antigas com tecnologia catódica. Aqui está uma foto minha ao lado dela.

Caso você esteja se perguntando, a diferença entre Loose Deuces e Double Deuces é que o primeiro paga 500 por quatro dois e o segundo 400.
Sei que em algumas mãos de vídeo poker existem situações em que duas jogadas são igualmente boas, sendo a melhor jogada possível. Por exemplo, com um dois pares em um par de dois curingas com pagamento integral, o jogador deve manter apenas um par, independentemente de qual seja. Minha pergunta é se existem situações em que três jogadas são igualmente boas, sendo a jogada correta?
Sim! No poker com curinga , com uma mão ruim, como regra geral é melhor manter uma das cartas do meio que tenha as melhores chances de formar uma sequência ou um flush. No entanto, às vezes é uma decisão difícil, ou até mesmo um empate, sobre qual é a melhor carta para se manter.
Por exemplo, na tabela de pagamento de 97,19% para dois pares com curinga no poker e uma Qh, 10d, 5d, 7c e 2c no draw, a melhor jogada é um empate entre segurar apenas o 10d, o 5d e o 7c, com um valor esperado de 0,240703 para as três cartas. Isso pode ser verificado usando meu analisador de mãos de vídeo poker .
Aqui estão outras jogadas semelhantes para a mesma tabela de pagamentos do joker poker:
- QC 10S 5D 7H 2C
- QH 10D 5D 7H 2C
- KH 10D 5D 8C 3C
- KC 10S 5D 8H 3C
- KH 10D 5D 8H 3C
Meus agradecimentos a Gary Koehler pela ajuda com esta questão.
Olá. Escrevo porque sou um grande fã de vídeo pôquer (embora eu não seja um jogador profissional e jogue apenas por diversão em simulações). Queria experimentar algumas simulações e achei sua página "Minha Metodologia para Análise de Vídeo Pôquer" extremamente útil. Apesar de ter levado algumas tentativas para realmente entender tudo, finalmente consegui escrever um pequeno simulador para jogar automaticamente e posso comparar meus resultados com os da sua página "Analisador de Mãos de Vídeo Pôquer" e obter as mesmas conclusões.
A página de metodologia, porém, aborda apenas um baralho padrão de 52 cartas, sem curingas. Tentei expandir o algoritmo por conta própria para permitir a adição de um a quatro curingas ao baralho, mas até agora os resultados têm sido lentos e imprecisos. Parte do problema reside no fato de que os curingas parecem adicionar muita complexidade, já que meu algoritmo substitui 52 possibilidades pelos curingas e, além disso, creio que o algoritmo não permita índices duplicados. Gostaria de saber se a página de metodologia poderia ser expandida para incluir dicas sobre como lidar com situações que envolvam curingas de maneira igualmente eficiente, como já ocorre com o baralho padrão.
Adorei o site e quero agradecer pela ajuda que ele me proporcionou até agora, pois acho que não teria conseguido concluir meu projeto sem ele. Tenha um ótimo dia!
Muito obrigado por todas as palavras gentis!
Percorrer todas as 52 maneiras de usar um curinga certamente será lento, especialmente se houver vários curingas. Veja como eu pontuo uma mão com curingas:
- Se você tiver um royal flush natural, pontue a mão dessa forma.
- Caso contrário, conte o número de curingas na mão.
- Em seguida, pontue a mão de acordo com esse número e o valor das outras cartas.
Por exemplo, suponha que você saiba que tem dois curingas. Você poderia usar este pseudocódigo para calcular a pontuação da mão com base nas outras três cartas:
- Se as três cartas forem do mesmo naipe e a mais baixa for pelo menos um dez, então você tem um curinga real.
- Caso contrário, se as três cartas forem do mesmo naipe e a diferença entre a mais alta e a mais baixa for de quatro ou menos, então você tem um straight flush.
- Caso contrário, se as três cartas forem do mesmo naipe, a mais alta for um ás e a segunda mais alta for um cinco ou menor, então você também terá um straight flush (A2345).
- Caso contrário, se você tiver um par, então terá uma quadra.
- Caso contrário, se as três cartas forem do mesmo naipe, você tem um flush.
- Caso contrário, se a diferença entre o maior e o menor for de quatro ou menos, então você tem uma sequência.
- Caso contrário, se a carta mais alta for um ás e a segunda mais alta for um cinco ou menos, então você também tem uma sequência (A2345).
- Caso contrário, você tem um par.
Você já tem o código para nenhum curinga, então precisará escrever um código separado para um a quatro ou cinco curingas, dependendo se deseja analisar os curingas Deuces e Joker .
Sei de uma promoção que paga um bônus após conseguir uma quadra em todas as 13 cartas do mesmo naipe. Quantas mãos são necessárias em média para isso?
Para responder à sua pergunta, vamos analisar o padrão ouro do vídeo pôquer, o 9-6 Jacks or Better .
O primeiro passo é modificar minha calculadora para incluir uma linha para cada uma das 13 quadras. Aqui está a tabela de retorno modificada:
Mesa de retorno modificada Jacks or Better
| Evento | Paga | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| Rubor Real | 800 | 493.512.264 | 0,000025 | 0,019807 |
| Straight flush | 50 | 2.178.883.296 | 0,000109 | 0,005465 |
| Quatro A | 25 | 3.900.253.596 | 0,000196 | 0,004892 |
| Quatro K | 25 | 3.904.533.816 | 0,000196 | 0,004897 |
| Quatro Q | 25 | 3.898.370.196 | 0,000196 | 0,004889 |
| Quatro J | 25 | 3.886.872.684 | 0,000195 | 0,004875 |
| Quatro 10 | 25 | 3.471.687.732 | 0,000174 | 0,004354 |
| Quatro 9 | 25 | 3.503.226.684 | 0,000176 | 0,004394 |
| Quatro 8 | 25 | 3.504.128.652 | 0,000176 | 0,004395 |
| Quatro 7 | 25 | 3.504.825.252 | 0,000176 | 0,004396 |
| Quatro 6 | 25 | 3.504.861.888 | 0,000176 | 0,004396 |
| Quatro 5 | 25 | 3.504.895.944 | 0,000176 | 0,004396 |
| Quatro 4 | 25 | 3.504.032.676 | 0,000176 | 0,004395 |
| Quatro 3 | 25 | 3.503.177.148 | 0,000176 | 0,004394 |
| Quatro 2 | 25 | 3.502.301.496 | 0,000176 | 0,004393 |
| Casa cheia | 9 | 229.475.482.596 | 0,011512 | 0,103610 |
| Descarga | 6 | 219.554.786.160 | 0,011015 | 0,066087 |
| Direto | 4 | 223.837.565.784 | 0,011229 | 0,044917 |
| Três de um tipo | 3 | 1.484.003.070.324 | 0,074449 | 0,223346 |
| Dois pares | 2 | 2.576.946.164.148 | 0,129279 | 0,258558 |
| Valetes ou melhor | 1 | 4.277.372.890.968 | 0,214585 | 0,214585 |
| Nada | 0 | 10.872.274.993.896 | 0,545435 | 0,000000 |
| Total | 19.933.230.517.200 | 1.000000 | 0,995439 |
A probabilidade de obter uma quadra qualquer é de 0,002363.
A próxima pergunta a ser respondida é: quantas quadras serão necessárias, em média, para obter todos os 13 tipos de cartas? Para responder a essa pergunta, criei minha Calculadora de Tentativas Esperadas . Para usá-la, insira o número de combinações de cada quadra nas primeiras 13 células. A calculadora informará que serão necessárias, em média, 41,532646 quadras para obter todos os 13 tipos de cartas.
Portanto, o número esperado de mãos jogadas para obter todas as 13 quadras é 41,341739/0,002363 = 17.580.
Qual é o custo de não jogar todas as quatro linhas no poker Multi-Strike ?
Vamos analisar o Bonus Poker 8-5 como exemplo. A tabela a seguir mostra o retorno por número de linhas apostadas.
- 4 linhas: 99,375%
- 3 linhas: 99,279%
- 2 linhas: 99,214%
- 1 linha: 99,166%
A lista seguinte mostra o custo de não jogar o número máximo de linhas, de acordo com a quantidade de linhas jogadas.
- 4 linhas: 0,000%
- 3 linhas: 0,095%
- 2 linhas: 0,160%
- 1 linha: 0,209%
Você sabia que os jogos de video poker Dream Card não fornecem a Dream Card correta no Bonus Poker quando as quatro cartas distribuídas são cinco singletons, sendo a mais baixa um quatro e as outras três menores que um valete, sem chance de sequência ou flush? A Dream Card correta seria o quatro, devido ao prêmio adicional de uma quadra de quatros. No entanto, a Dream Card fornecida será de outro valor. Qual é o custo dessa Dream Card incorreta, supondo que o jogador sempre a aceite?
Sim, eu estava ciente disso. Para o benefício dos outros leitores, no Dream Card, o jogo às vezes oferece a 5ª carta ideal com base nas quatro primeiras cartas distribuídas aleatoriamente. A probabilidade de obter um Dream Card no Bonus Poker é de 46,7%. O jogador sempre pode rejeitar o Dream Card sugerido e trocar por qualquer outra carta ainda disponível no baralho. No entanto, a recomendação está sempre correta, pelo que sei, exceto nesta situação específica do Bonus Poker.
Se o jogador receber a Carta dos Sonhos, a probabilidade de as outras quatro cartas resultarem nessa situação é de 1,49%. Considerando a probabilidade de 46,7% de se obter a Carta dos Sonhos, essa situação ocorrerá com probabilidade de 0,70%, ou seja, uma vez a cada 144 mãos.
Usando meu analisador de mãos de vídeo pôquer , o valor esperado de um par de quatros no Bonus Poker 8/5 é 0,855134. O valor esperado de um par de 5 a 10 é 0,813506. Portanto, o custo do bug cada vez que ele ocorre, supondo que o jogador aceite a Carta dos Sonhos, é de 0,041628 em valor esperado.
O custo total para o retorno do jogo é de 0,006955 × 0,041628 = 0,000290, ou cerca de 0,03%.
Qual é a probabilidade de um royal flush se o jogador sempre comprar uma mão que já tenha uma carta? Considere que o jogador sempre escolhe o naipe com o maior número de cartas que já formam um royal flush.
A tabela a seguir mostra a probabilidade de ter de 0 a 5 cartas para formar uma realeza na distribuição inicial, assumindo que o jogador sempre escolhe o naipe que já possui o maior número de cartas para formar uma realeza, a probabilidade de completar a realeza e o produto.
Jogador Royal or Nothing
| Cartão para Royal em promoção | Negócio Probabilidade | Probabilidade Realeza Completa | Produto |
|---|---|---|---|
| 0 | 0,61538462 | 0,00000261 | 0,00000160 |
| 1 | 0,35444947 | 0,00003064 | 0,00001086 |
| 2 | 0,02835596 | 0,00070472 | 0,00001998 |
| 3 | 0,00173608 | 0,01057082 | 0,00001835 |
| 4 | 0,00007234 | 0,11627907 | 0,00000841 |
| 5 | 0,00000154 | 1.00000000 | 0,00000154 |
| Total | 1.00000000 | 0,00006075 |
A célula inferior direita mostra que um jogador que aposta "tudo ou nada" tem uma probabilidade de formar um royal flush de 0,000006075, ou 1 em 16.461.
Qual seria a probabilidade de um Royal Flush no vídeo pôquer se o jogador pudesse ver as próximas cartas a serem distribuídas?
Vamos supor que o jogo escolha cinco cartas aleatórias para o descarte, que ficarão em uma fila esperando o jogador descartá-las. Por exemplo, se o jogador descartar três, ele receberá as próximas três da fila. A resposta é a mesma, aliás, se houver uma carta específica na distribuição inicial atribuída a cada carta no descarte. Dito isso, a tabela a seguir mostra a probabilidade de formar um Royal Flush com cada número na distribuição inicial, a probabilidade de completá-lo no descarte e o produto. A célula inferior direita mostra uma probabilidade geral de 0,00006075, que equivale a 1 em 16.461.
O jogador perfeito no vídeo pôquer
| Cartão para Royal em promoção | Negócio Probabilidade | Probabilidade Realeza Completa | Produto |
|---|---|---|---|
| 0 | 0,61538462 | 0,00000261 | 0,00000160 |
| 1 | 0,35444947 | 0,00003064 | 0,00001086 |
| 2 | 0,02835596 | 0,00070472 | 0,00001998 |
| 3 | 0,00173608 | 0,01057082 | 0,00001835 |
| 4 | 0,00007234 | 0,11627907 | 0,00000841 |
| 5 | 0,00000154 | 1.00000000 | 0,00000154 |
| Total | 1.00000000 | 0,00006075 |
Na sua explicação sobre uma máquina de video poker com cartelas raspadas , você dá o seguinte exemplo: "Mesmo que o jogo pareça um video poker de cinco cartas, o resultado é predeterminado. Por exemplo, se você receber um royal flush na distribuição inicial e descartar todas as cartas, receberá outro royal flush na próxima rodada." Minha pergunta é: o que acontece se você descartar cartas que tornam um resultado predeterminado impossível (como um dois no Deuces Wild para um 4-Dues predeterminado ou um Ás em um jogo Double Bonus para 4 Áses?) Talvez esses tipos de jogos não sejam oferecidos, mas apenas aqueles, como Jacks or Better, onde tal situação não é possível?
O que eu ouvi dizer que acontece é que uma fada aparece e muda sua mão na hora de comprar as cartas para o que quer que estivesse predestinado. Por exemplo, se você estivesse predestinado a receber dois dois na distribuição inicial e melhorar para quatro dois depois da compra, se você descartasse os dois, provavelmente receberia os outros dois naturalmente na compra, e então a fada trocaria duas cartas ruins pelos dois dois que você descartou.
No vídeo poker, com que frequência um jogador terá de 0 a 5 cartas para um royal flush após a distribuição das cartas?
A resposta é um tanto complexa, pois existem diversas maneiras pelas quais o jogador pode ter a possibilidade de formar uma sequência real, após a distribuição das cartas, em diferentes naipes. Presumo que o jogador sempre mantenha as cartas do naipe com a maior probabilidade de formar uma sequência real e escolha aleatoriamente caso dois ou mais naipes estejam empatados com o maior número de cartas para formar uma sequência real. Dito isso, permita-me definir algumas abreviações:
- Cartas reais = cartas de valor 10 ao ás.
- H = Cartas reais em copas.
- S = Cartas reais em copas.
- C = Cartas reais em copas.
- D = Cartas reais em copas.
- x = Cartão não real
A tabela a seguir mostra o número de combinações de cada situação possível. Uma linha incluirá todos os casos matematicamente equivalentes. Por exemplo, Hxxxx incluirá ter apenas uma carta para um naipe real em qualquer naipe (não apenas copas).
Combinações para Royal após o acordo
| Mão | Cartas para a realeza | Combinações |
|---|---|---|
| HHHHH | 5 | 4 |
| HHHHS | 4 | 300 |
| HHHHx | 4 | 640 |
| HHHSS | 3 | 1.200 |
| HHHSC | 3 | 3.000 |
| HHHSx | 3 | 19.200 |
| HHHxx | 3 | 19.840 |
| HHSSC | 2 | 6.000 |
| HHSSx | 2 | 19.200 |
| HHSCD | 2 | 5.000 |
| HHSCx | 2 | 96.000 |
| HHSxx | 2 | 297.600 |
| HHxxx | 2 | 198.400 |
| HSCDx | 1 | 20.000 |
| HSCxx | 1 | 248.000 |
| HSxxx | 1 | 744.000 |
| Hxxxx | 1 | 719.200 |
| xxxxx | 0 | 201.376 |
| Total | 2.598.960 |
A próxima tabela mostra a probabilidade geral de ter de 0 a 5 cartas para formar uma realeza após a distribuição das cartas.
Cartas para Probabilidades Reais
| Cartas para a realeza | Probabilidade |
|---|---|
| 5 | 0,0002% |
| 4 | 0,0362% |
| 3 | 1,6637% |
| 2 | 23,9403% |
| 1 | 66,6113% |
| 0 | 7,7483% |
| Total | 100,0000% |
Não que você tenha perguntado, mas se um jogador seguisse uma estratégia de "tudo ou nada", a probabilidade de ele conseguir um royal flush por mão seria de 1 em 23.162.
Se eu estiver usando a estratégia de apostas perfeita para jogar video poker, qual jogo me dá a melhor chance de conseguir um royal flush?
Para efeito de comparação, a probabilidade de um Royal Flush no video poker convencional varia de aproximadamente 1 em 40.000 a 45.000, considerando a estratégia ideal. Aqui estão alguns números exatos para jogos selecionados aleatoriamente:
- 9-6 Valetes ou melhor: 1 em 40.391
- 25-15-9-4-4-3 (Illinois) Deuces Wild — 1 em 43.423
- Bônus Triplo Duplo 9-7: 1 em 45.358
Para os jogadores ávidos por um Royal Flush, a probabilidade aumenta significativamente em Chase the Royal . Esta é uma variante antiga de vídeo pôquer onde o jogador pode trocar um par de figuras (valete, dama e rei) por três cartas para formar um Royal Flush na distribuição inicial. Para tornar a troca vantajosa, o jogo aumenta o prêmio para sequências e flushes, caso você faça a troca. A probabilidade exata de um Royal Flush dependerá do jogo base e da tabela de pagamentos. A probabilidade é maximizada com um jogo base Triple Bonus e tabela de pagamentos 8-5, com uma frequência de Royal Flush de 1 em 9.151. Isso inclui tanto o Royal Flush na distribuição inicial, que paga 800 por 1 carta, com uma frequência de 1 em 9.282, quanto o Royal Flush na distribuição inicial, que paga 2.000 por 1 carta, com uma frequência de 1 em 649.773.
No entanto, a situação fica ainda melhor se considerarmos jogos em que o jogador precisa pagar uma taxa equivalente à sua aposta base para ativar um recurso. No Draw Poker com Dream Card (não confundir com Dream Card Poker ), o jogador frequentemente recebe a carta dos seus sonhos (supondo que seja um matemático sonhando) como a quinta carta da distribuição. A probabilidade de obter a Dream Card é maximizada no Jacks or Better, com 50,5%. No Jacks or Better 9-6, a frequência geral de um Royal Flush é de 1 em 8.105. Lembre-se de que, com a taxa para ativar o recurso, o ganho efetivo em um Royal Flush cai para 400 para 1.
Enquanto eu mencionar Dream Card Poker (um jogo diferente de Draw Poker com Dream Card), a frequência de Royale nesse jogo não é tão alta. Aparentemente, ela é mais alta em 11-8-6 Jacks or Better, com 1 em 15.034.
Esta resposta não leva em consideração o Movin' On Up Poker , um jogo de video poker antigo e pouco conhecido onde o jogador recebe duas ou três rodadas extras, em vez de uma. Não sei a frequência do Royal Flush nesse jogo, mas no Triple Draw, em que o jogador precisa pagar uma taxa equivalente a cinco vezes sua aposta base para habilitar as duas rodadas extras, estimo que seja aproximadamente 1 em 4.000.
Em resumo, se não considerarmos jogos em que o jogador precisa pagar uma taxa extra para ativar algum tipo de artifício, minha resposta é Chase the Royal.
Qual é o custo em erros do jogador se eu jogar a estratégia ideal para Not so Ugly Ducks em Illinois Deuces?
Para relembrar, aqui estão as tabelas salariais mencionadas:
Patinhos nem tão feios: 1-2-3-4-4-10-16-25-200-800.
Duques de Illinois: 1-2-3-4-4-9-15-25-200-800
A seguir, apresentamos a tabela de retorno para o jogo Not so Ugly Ducks, seguindo a estratégia ideal para esse jogo.
Patos não tão feios -- Estratégia correta
| Evento | Paga | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| sequência real natural | 800 | 458.696.304 | 0,000023 | 0,018409 |
| Quatro dois | 200 | 3.721.737.204 | 0,000187 | 0,037342 |
| sequência real selvagem | 25 | 38.006.962.464 | 0,001907 | 0,047668 |
| Cinco de um tipo | 16 | 61.961.233.656 | 0,003108 | 0,049735 |
| Straight flush | 10 | 102.392.435.976 | 0,005137 | 0,051368 |
| Quatro de um mesmo tipo | 4 | 1.216.681.289.508 | 0,061038 | 0,244151 |
| Casa cheia | 4 | 520.566.943.104 | 0,026116 | 0,104462 |
| Descarga | 3 | 413.870.908.056 | 0,020763 | 0,062289 |
| Direto | 2 | 1.142.885.476.800 | 0,057336 | 0,114671 |
| Três de um tipo | 1 | 5.325.911.611.716 | 0,267188 | 0,267188 |
| Nada | 0 | 11.106.773.222.412 | 0,557199 | 0,000000 |
| Total | 19.933.230.517.200 | 1.000000 | 0,997283 |
A seguir, apresentamos a tabela de retorno para Illinois Deuces, utilizando a estratégia correta para essa tabela de pagamentos. A célula inferior direita mostra um retorno de 0,989131.
Illinois Deuces -- Estratégia Correta
| Evento | Paga | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| sequência real natural | 800 | 459.049.128 | 0,000023 | 0,018423 |
| Quatro dois | 200 | 3.727.422.492 | 0,000187 | 0,037399 |
| sequência real selvagem | 25 | 38.117.987.136 | 0,001912 | 0,047807 |
| Cinco de um tipo | 15 | 62.201.557.608 | 0,003120 | 0,046807 |
| Straight flush | 9 | 98.365.859.016 | 0,004935 | 0,044413 |
| Quatro de um mesmo tipo | 4 | 1.221.942.888.444 | 0,061302 | 0,245207 |
| Casa cheia | 4 | 522.030.131.520 | 0,026189 | 0,104756 |
| Descarga | 3 | 407.586.633.720 | 0,020448 | 0,061343 |
| Direto | 2 | 1.145.767.137.120 | 0,057480 | 0,114961 |
| Três de um tipo | 1 | 5.342.397.992.292 | 0,268015 | 0,268015 |
| Nada | 0 | 11.090.633.858.724 | 0,556389 | 0,000000 |
| Total | 19.933.230.517.200 | 1.000000 | 0,989131 |
A próxima tabela mostra a tabela de retorno usando as combinações e probabilidades de Not so Ugly Ducks na tabela de pagamento para Illinois Deuces. A célula inferior direita mostra um retorno de 0,989131.
Illinois Deuces - Estratégia NSUD
| Evento | Paga | Combinações | Probabilidade | Retornar |
|---|---|---|---|---|
| sequência real natural | 800 | 458.696.304 | 0,000023 | 0,018409 |
| Quatro dois | 200 | 3.721.737.204 | 0,000187 | 0,037342 |
| sequência real selvagem | 25 | 38.006.962.464 | 0,001907 | 0,047668 |
| Cinco de um tipo | 15 | 61.961.233.656 | 0,003108 | 0,046627 |
| Straight flush | 9 | 102.392.435.976 | 0,005137 | 0,046231 |
| Quatro de um mesmo tipo | 4 | 1.216.681.289.508 | 0,061038 | 0,244151 |
| Casa cheia | 4 | 520.566.943.104 | 0,026116 | 0,104462 |
| Descarga | 3 | 413.870.908.056 | 0,020763 | 0,062289 |
| Direto | 2 | 1.142.885.476.800 | 0,057336 | 0,114671 |
| Três de um tipo | 1 | 5.325.911.611.716 | 0,267188 | 0,267188 |
| Nada | 0 | 11.106.773.222.412 | 0,557199 | 0,000000 |
| Total | 19.933.230.517.200 | 1.000000 | 0,989038 |
O custo dos erros é o retorno ótimo para Illinois Deuces (segunda tabela) menos o retorno para Illinois Deuces usando a estratégia NSUD (terceira tabela) = 0,989131 - 0,989038 = 0,000093.
Li sobre o jogo Reversible Royal com retorno de 105,22% no seu artigo no Wizard of Vegas. Esse retorno pressupõe uma estratégia ótima, incluindo a ordem das cartas. Qual seria o retorno se eu considerasse uma vitória média em um Royal Flush? E se eu usasse a estratégia comum do Bonus Poker 6-5, que é a tabela de pagamento básica?
Considerando que não haja desvios de estratégia, 1 em cada 60 Royals será sequencial. O jackpot do Royal reversível paga 161.556 por 1. Qualquer outro Royal paga 800 por 1. O ganho médio do Royal é, portanto, (1/60)*161.556 + (59/60)*800 + 17.396 por 1.
Se assumirmos que todos os Royals pagam 17.396 e jogarmos a estratégia ideal com base nessa vitória do Royal, o retorno cai para 103,56%.
Se jogarmos com a estratégia padrão de Bonus Poker 6-5, que é a tabela de pagamento base, o retorno cai ainda mais para 101,97%.
Em suas dicas de programação de vídeo pôquer , você explica que, embora existam 2.598.960 mãos iniciais possíveis no vídeo pôquer, com um baralho de 52 cartas, existem apenas 134.459 classes de mãos que precisam ser analisadas.
Minha pergunta é: quantas classes existem para o poker joker?
Para esta questão, recorri ao meu estimado colega, Gary Koehler, especialista em matemática do video poker. Aqui estão as respostas dele, de acordo com o número de curingas:
- 1 Coringa: 150.891
- 2 Coringas: 169.078
- 3 Coringas: 189.189
- 4 Coringas: 211.406
- 5 Coringas: 235.925
Em suas dicas de programação para video poker , você explica que, embora existam 2.598.960 mãos iniciais possíveis em video poker com um baralho de 52 cartas, existem apenas 134.459 classes de mãos necessárias para analisar. Minha pergunta é: se alguém estivesse jogando um jogo onde a ordem das cartas importa, como Ace$ Bonus Poker ou um com um jackpot para um royal flush sequencial , quantas classes diferentes de mãos seriam necessárias para analisar?
Para esta questão, recorri ao meu estimado colega, Gary Koehler, que é especialista em matemática de video poker. A resposta dele é 15.019.680.
Qual é o número médio de cartas que o jogador mantém após o descarte no vídeo pôquer?
A tabela a seguir mostra o número médio de cartas na mão em 10 jogos diferentes e suas respectivas tabelas de pagamento. A média dos jogos listados é 2,05.
Número médio de cartas na mão no vídeo pôquer
| Jogo | Tabela de Pagamento | Retornar | Av. Cartões Segurados |
|---|---|---|---|
| Bônus Dois | 10-4-3-3 | 97,36% | 1,845550 |
| Deuces Wild | 25-15-9-5-3 | 100,76% | 1,926010 |
| Ás em chamas | 9-5 | 99,57% | 2,055630 |
| Super Duplo Duplo Bônus | 7-5 | 99,17% | 2,057280 |
| Bônus Duplo Duplo | 9-5 | 97,87% | 2,058390 |
| Bônus Triplo Duplo | 8-5 | 95,97% | 2.072620 |
| Bônus Poker | 8-5 | 99,17% | 2.080610 |
| Valetes ou Melhor | 9-5 | 98,45% | 2.081030 |
| Bônus Poker Deluxe | 8-5 | 97,40% | 2,150470 |
| Bônus Duplo | 9-6-5 | 97,81% | 2,173550 |
Sei que, ao ganhar US$ 1.200 ou mais em uma máquina caça-níqueis, você tem a opção de receber o pagamento por cheque. Dito isso, digamos, para fins de argumentação, que eu queira converter dinheiro em cheques emitidos por um cassino. Suponha que eu jogue Jacks or Better 9/6 perfeitamente com uma aposta de US$ 25 (ou US$ 125 no total). Quanto do meu dinheiro eu poderia esperar perder ao convertê-lo em cheques?
Para a combinação 9-6 Jacks or Better, você ganhará $1200 ou mais a cada quadra ou combinação superior. O retorno para uma casa cheia ou inferior é de 0,911103. Você terá que apostar seu saldo inicial 1/(1-0,911103) = 11,249016 vezes até que seu dinheiro seja convertido em cheque ou perdido devido à vantagem da casa. A vantagem da casa é de 0,004561. Portanto, você pode esperar perder 0,004561 × 11,249016 = 0,051306 vezes o seu saldo inicial.
Curiosamente, o custo para converter dinheiro em cheques é menor no 9-6 Double Double Bonus, apesar da maior vantagem da casa. Esse jogo oferece prêmios maiores para quadras, então seus cheques são maiores. Nesse jogo, o retorno de uma quadra cheia ou menos é de 0,777138. Isso significa que você terá que girar seu saldo 1/(1-0,777138) = 4,487076 vezes para convertê-lo em cheque. A vantagem da casa no 9-6 Double Double Bonus é de 0,010192. Portanto, a perda esperada ao converter para dinheiro é de 4,487076 × 0,010192 = 0,045733.
Você poderia reduzir ainda mais os custos com desvios de estratégia que visem quadras ou cartas superiores, mas deixarei isso como um exercício para o leitor.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Qual é a probabilidade de ganhar um jackpot (prêmio de US$ 1.200 ou mais) no jogo Jacks or Better 9/6 em video poker com vários jogadores?
É claro que isso depende do valor da aposta e do número de jogadas. A tabela a seguir mostra essas probabilidades.
Probabilidade de ganhar o jackpot no vídeo pôquer com várias rodadas
| Denominação | 3 Play | 5 Play | 10 Play | 25 Jogar | 50 Play | 100 Play |
|---|---|---|---|---|---|---|
| $ 0,01 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000001 | 0,000001 |
| $ 0,05 | 0,000000 | 0,000000 | 0,000001 | 0,000001 | 0,000002 | 0,000022 |
| $ 0,10 | 0,000001 | 0,000001 | 0,000002 | 0,000006 | 0,000047 | 0,000378 |
| $ 0,25 | 0,000002 | 0,000003 | 0,000008 | 0,000053 | 0,000369 | 0,000556 |
| $ 0,50 | 0,000070 | 0,000115 | 0,000238 | 0,000782 | 0,001247 | 0,008527 |
| $ 1,00 | 0,000070 | 0,000128 | 0,000473 | 0,000786 | 0,009518 | 0,072671 |
| $ 2,00 | 0,000083 | 0,000363 | 0,000488 | 0,010002 | 0,070029 | 0,239753 |
| $ 5,00 | 0,000720 | 0,001290 | 0,012978 | 0,100374 | 0,318838 | 0,768839 |
| $ 25,00 | 0,041494 | 0,124818 | 0,348811 | 0,835708 | 0,995943 | 0,999983 |
Esta tabela foi retirada do meu apêndice 2 sobre vídeo poker , onde mostro com que frequência o jogador obtém cada vitória total em uma simulação de grande escala.