Nesta página
Encouraçado
Introdução
Battleship é um jogo ao vivo da Atmosfera, uma empresa de software que fornece jogos para cassinos online. O jogo é vagamente baseado no jogo de tabuleiro que joguei milhares de vezes quando criança. Ao contrário do jogo de tabuleiro, neste jogo, todos os navios, independentemente do tamanho, são chamados de navios de guerra.
Regras
- O jogo é jogado em um cartão de 10x9, com quadrados numerados de 1 a 90.
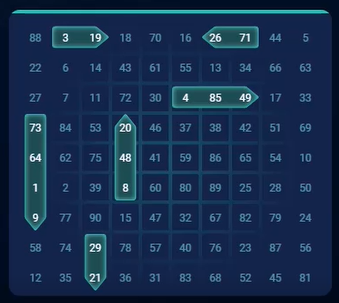
- Cada carta contém um navio de guerra 4x1, dois navios de guerra 3x1 e três navios de guerra 2x1. O jogador pode escolher o posicionamento dos navios ou deixar que o jogo o faça aleatoriamente.
- O jogador pode jogar com 1 a 1.000 cartas e optar por apostar de US$ 0,50 a US$ 5 por carta.
- Após o encerramento das apostas, o jogo sorteará 70 números, sem reposição, de um recipiente contendo bolas numeradas de 1 a 90.
- Se uma bola sorteada corresponder a um número em que um navio de guerra esteja ancorado, esse número será considerado "marcado".
- Se um navio de guerra estiver completamente marcado, diz-se que foi afundado.
- A primeira das quatro maneiras de ganhar é chamada de Jackpot, que paga 300 para 1. O jogador ganha se afundar o navio de guerra 4x1 nas primeiras 10 bolas.
- A segunda das quatro maneiras de ganhar se chama Batalha Naval. O jogador vence se afundar pelo menos dois navios que cubram de 4 a 7 quadrados entre eles. A vitória dependerá do número de quadrados entre os navios afundados e do número de bolas necessárias para isso, conforme mostrado na tabela de pagamentos abaixo.
- A terceira das quatro maneiras de ganhar se chama Frota. O jogador vence de acordo com a quantidade de bolas necessárias para afundar todos os seis navios. A vitória depende do número de bolas necessárias para isso.
- A quarta das quatro maneiras de ganhar se chama Frota Bônus. O jogador ganha de acordo com a quantidade de bolas necessárias para marcar todos os quadrados em todos os navios, exceto no quadrado . A vitória depende do número de bolas necessárias para isso.
A tabela a seguir mostra a tabela de pagamentos para vitórias em batalhas navais. Lembrando que quatro quadrados representam um escalão, cinco representam uma divisão, seis representam uma brigada e sete representam um esquadrão.
Tabela de Pagamento de Navios de Guerra
| Bolas | Escalão | Divisão | Brigada | Esquadrão |
|---|---|---|---|---|
| 4 a 10 | 40 | 50 | 60 | 24 |
| 11 a 15 | 12 | 50 | 60 | 24 |
| 16 a 20 | 5 | 14 | 60 | 24 |
| 21 a 25 | 2 | 6 | 16 | 24 |
| 26 a 30 | 1 | 3 | 8 | 10 |
| 31 a 35 | 0 | 1 | 4 | 5 |
| 36 a 40 | 0 | 0 | 2 | 3 |
| 41 a 45 | 0 | 0 | 0 | 1 |
Tabela de Pagamento de Frota e Frota Bônus
| Bolas | Frota | Frota de bônus |
|---|---|---|
| 1 a 50 | 300 | 40 |
| 51 a 55 | 100 | 10 |
| 56 a 60 | 40 | 4 |
| 61 a 65 | 10 | 2 |
| 66 a 70 | 4 | 1 |
A seguir, estão capturas de tela das tabelas de pagamento do jogo. A captura de tela da Brigada não mostra uma combinação de um navio de 4 quadrados e um de 2 quadrados, que conta. Observe como o exemplo da Frota Bônus está faltando um ponto de um dos navios de 3 quadrados, para mostrar que o jogador precisa obter 15 dos 16 quadrados.
 | 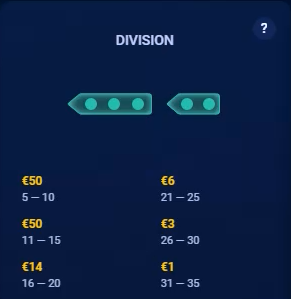 |  | ||
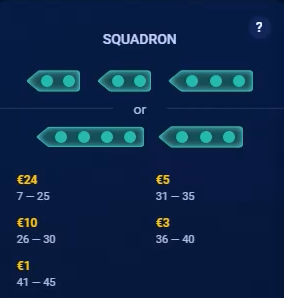 |  |  |
Análise do Jackpot
A probabilidade de afundar o navio de guerra 4x1 em 10 bolas é combin(86,6)/combin(90,10) = 1 em 12.168. Com uma vitória de 300, o retorno esperado deste recurso é 300/12168 = 2,47%.
Análise de Encouraçado
Análise de Escalão
Um escalão é qualquer conjunto de dois navios de guerra 2x1, que cobririam quatro quadrados. Com três navios de guerra 2x1, existem três combinações possíveis, escolhendo 2 entre 3. A tabela a seguir mostra a probabilidade de vitória com exatamente 4 a 30 bolas para qualquer escalão, a vitória e a contribuição para o retorno (produto da vitória e da probabilidade).
A célula inferior direita mostra um ganho esperado de 0,027405 por Echelon. Com três combinações de Echelons, o retorno total dos Echelons é 3 * 0,027405 = 0,082215.
Análise de Escalão
| Bolas | Paga | Probabilidade | Retornar |
|---|---|---|---|
| 4 | 40 | 0,000000 | 0,000016 |
| 5 | 40 | 0,000002 | 0,000063 |
| 6 | 40 | 0,000004 | 0,000157 |
| 7 | 40 | 0,000008 | 0,000313 |
| 8 | 40 | 0,000014 | 0,000548 |
| 9 | 40 | 0,000022 | 0,000877 |
| 10 | 40 | 0,000033 | 0,001315 |
| 11 | 12 | 0,000047 | 0,000564 |
| 12 | 12 | 0,000065 | 0,000775 |
| 13 | 12 | 0,000086 | 0,001033 |
| 14 | 12 | 0,000112 | 0,001343 |
| 15 | 12 | 0,000142 | 0,001709 |
| 16 | 5 | 0,000178 | 0,000890 |
| 17 | 5 | 0,000219 | 0,001096 |
| 18 | 5 | 0,000266 | 0,001331 |
| 19 | 5 | 0,000319 | 0,001597 |
| 20 | 5 | 0,000379 | 0,001896 |
| 21 | 2 | 0,000446 | 0,000892 |
| 22 | 2 | 0,000521 | 0,001041 |
| 23 | 2 | 0,000603 | 0,001205 |
| 24 | 2 | 0,000693 | 0,001386 |
| 25 | 2 | 0,000792 | 0,001584 |
| 26 | 1 | 0,000900 | 0,000900 |
| 27 | 1 | 0,001018 | 0,001018 |
| 28 | 1 | 0,001145 | 0,001145 |
| 29 | 1 | 0,001282 | 0,001282 |
| 30 | 1 | 0,001430 | 0,001430 |
| 31 a 90 | 0 | 0,989275 | 0,000000 |
| Total | 1.000000 | 0,027405 |
Análise de Divisão
Uma Divisão consiste em um navio de guerra 2x1 e um navio de guerra 3x1, que juntos cobririam cinco quadrados no total. Com três navios de guerra 2x1 e dois navios de guerra 3x1, existem seis maneiras de escolher um de cada tamanho. A tabela a seguir mostra a probabilidade de vitória com 5 a 35 bolas para qualquer Divisão, a vitória e a contribuição para o retorno (produto da vitória e da probabilidade).
A célula inferior direita mostra um ganho esperado de 0,022780 por Divisão. Com três combinações de Escalões, o retorno total das Divisões é 6 * 0,022780 = 0,136681.
Análise de Divisão
| Bolas | Paga | Probabilidade | Retornar |
|---|---|---|---|
| 4 | 40 | 0,000000 | 0,000016 |
| 5 | 40 | 0,000002 | 0,000063 |
| 6 | 40 | 0,000004 | 0,000157 |
| 7 | 40 | 0,000008 | 0,000313 |
| 8 | 40 | 0,000014 | 0,000548 |
| 9 | 40 | 0,000022 | 0,000877 |
| 10 | 40 | 0,000033 | 0,001315 |
| 11 | 12 | 0,000047 | 0,000564 |
| 12 | 12 | 0,000065 | 0,000775 |
| 13 | 12 | 0,000086 | 0,001033 |
| 14 | 12 | 0,000112 | 0,001343 |
| 15 | 12 | 0,000142 | 0,001709 |
| 16 | 5 | 0,000178 | 0,000890 |
| 17 | 5 | 0,000219 | 0,001096 |
| 18 | 5 | 0,000266 | 0,001331 |
| 19 | 5 | 0,000319 | 0,001597 |
| 20 | 5 | 0,000379 | 0,001896 |
| 21 | 2 | 0,000446 | 0,000892 |
| 22 | 2 | 0,000521 | 0,001041 |
| 23 | 2 | 0,000603 | 0,001205 |
| 24 | 2 | 0,000693 | 0,001386 |
| 25 | 2 | 0,000792 | 0,001584 |
| 26 | 1 | 0,000900 | 0,000900 |
| 27 | 1 | 0,001018 | 0,001018 |
| 28 | 1 | 0,001145 | 0,001145 |
| 29 | 1 | 0,001282 | 0,001282 |
| 30 | 1 | 0,001430 | 0,001430 |
| 31 a 90 | 0 | 0,989275 | 0,000000 |
| Total | 1.000000 | 0,027405 |
Análise da Brigada
Uma Brigada é qualquer combinação de dois ou três navios que cubram um total de seis quadrados. Isso pode ser três navios 2x1, dois navios 3x1 ou um navio 4x1 e um navio 2x1. Há uma maneira de escolher todos os três navios 2x1, uma maneira de escolher ambos os navios 3x1 e três maneiras de escolher o navio 4x1 e qualquer um dos navios 2x1. O número total de maneiras de se obter essa combinação é 1 + 1 + 3 = 5. A tabela a seguir mostra a probabilidade de ganhar com exatamente 6 a 40 bolas para qualquer Brigada, a vitória e a contribuição para o retorno (produto da vitória e da probabilidade).
A célula inferior direita mostra um ganho esperado de 0,026373 por Brigada. Com cinco combinações de Brigadas, o retorno total das Brigadas 5 * 0,026373 = 0,131867.
Análise da Brigada
| Bolas | Paga | Probabilidade | Retornar |
|---|---|---|---|
| 5 | 50 | 0,000000 | 0,000001 |
| 6 | 50 | 0,000000 | 0,000006 |
| 7 | 50 | 0,000000 | 0,000017 |
| 8 | 50 | 0,000001 | 0,000040 |
| 9 | 50 | 0,000002 | 0,000080 |
| 10 | 50 | 0,000003 | 0,000143 |
| 11 | 50 | 0,000005 | 0,000239 |
| 12 | 50 | 0,000008 | 0,000375 |
| 13 | 50 | 0,000011 | 0,000563 |
| 14 | 50 | 0,000016 | 0,000813 |
| 15 | 50 | 0,000023 | 0,001139 |
| 16 | 14 | 0,000031 | 0,000435 |
| 17 | 14 | 0,000041 | 0,000580 |
| 18 | 14 | 0,000054 | 0,000758 |
| 19 | 14 | 0,000070 | 0,000975 |
| 20 | 14 | 0,000088 | 0,001235 |
| 21 | 6 | 0,000110 | 0,000661 |
| 22 | 6 | 0,000136 | 0,000817 |
| 23 | 6 | 0,000166 | 0,000999 |
| 24 | 6 | 0,000201 | 0,001209 |
| 25 | 6 | 0,000242 | 0,001451 |
| 26 | 3 | 0,000288 | 0,000863 |
| 27 | 3 | 0,000340 | 0,001020 |
| 28 | 3 | 0,000399 | 0,001198 |
| 29 | 3 | 0,000466 | 0,001398 |
| 30 | 3 | 0,000540 | 0,001621 |
| 31 | 1 | 0,000624 | 0,000624 |
| 32 | 1 | 0,000716 | 0,000716 |
| 33 | 1 | 0,000818 | 0,000818 |
| 34 | 1 | 0,000931 | 0,000931 |
| 35 | 1 | 0,001055 | 0,001055 |
| 36+ | 0 | 0,001191 | 0,000000 |
| 36+ | 1.000000 | 0,022780 |
Análise de Esquadrão
Um Esquadrão é qualquer combinação de duas ou três naves que cubram um total de sete quadrados. Isso pode ser obtido com duas naves 2x1 e uma 3x1, ou com uma nave 4x1 e uma 3x1. Existem três maneiras de escolher 2 de 3 naves 2x1 e duas maneiras de escolher uma nave 3x1, totalizando 3*2=6 maneiras de escolher naves em uma configuração 2+2+3=7. Existem duas maneiras de escolher duas de duas naves 3x1 e uma maneira de escolher a nave 4x1, totalizando 2*1=2 maneiras de escolher naves na configuração 4+3. O número total de maneiras de se obter essa configuração é 6+2=8. A tabela a seguir mostra a probabilidade de ganhar com exatamente 7 a 45 bolas para qualquer Esquadrão, a vitória e a contribuição para o retorno (produto da vitória e da probabilidade).
A célula inferior direita mostra um ganho esperado de 0,015128 por Esquadrão. Com cinco combinações de Esquadrões, o retorno total dos Esquadrões 8 * 0,015128 = 0,121021.
Análise de Esquadrão
| Bolas | Paga | Probabilidade | Retornar |
|---|---|---|---|
| 7 | 24 | 0,000000 | 0,000000 |
| 8 | 24 | 0,000000 | 0,000000 |
| 9 | 24 | 0,000000 | 0,000000 |
| 10 | 24 | 0,000000 | 0,000000 |
| 11 | 24 | 0,000000 | 0,000001 |
| 12 | 24 | 0,000000 | 0,000001 |
| 13 | 24 | 0,000000 | 0,000003 |
| 14 | 24 | 0,000000 | 0,000006 |
| 15 | 24 | 0,000000 | 0,000010 |
| 16 | 24 | 0,000001 | 0,000016 |
| 17 | 24 | 0,000001 | 0,000026 |
| 18 | 24 | 0,000002 | 0,000040 |
| 19 | 24 | 0,000002 | 0,000060 |
| 20 | 24 | 0,000004 | 0,000087 |
| 21 | 24 | 0,000005 | 0,000125 |
| 22 | 24 | 0,000007 | 0,000174 |
| 23 | 24 | 0,000010 | 0,000240 |
| 24 | 24 | 0,000014 | 0,000324 |
| 25 | 24 | 0,000018 | 0,000432 |
| 26 | 10 | 0,000024 | 0,000237 |
| 27 | 10 | 0,000031 | 0,000308 |
| 28 | 10 | 0,000040 | 0,000396 |
| 29 | 10 | 0,000050 | 0,000504 |
| 30 | 10 | 0,000064 | 0,000636 |
| 31 | 5 | 0,000079 | 0,000397 |
| 32 | 5 | 0,000099 | 0,000493 |
| 33 | 5 | 0,000121 | 0,000606 |
| 34 | 5 | 0,000148 | 0,000741 |
| 35 | 5 | 0,000180 | 0,000900 |
| 36 | 3 | 0,000217 | 0,000652 |
| 37 | 3 | 0,000261 | 0,000782 |
| 38 | 3 | 0,000311 | 0,000933 |
| 39 | 3 | 0,000370 | 0,001109 |
| 40 | 3 | 0,000437 | 0,001310 |
| 41 | 1 | 0,000514 | 0,000514 |
| 42 | 1 | 0,000602 | 0,000602 |
| 43 | 1 | 0,000702 | 0,000702 |
| 44 | 1 | 0,000816 | 0.000816 |
| 45 | 1 | 0,000945 | 0,000945 |
| 46+ | 0 | 0,993926 | 0,000000 |
| Total | 1.000000 | 0,015128 |
Análise de frota
A tabela a seguir mostra minha análise de como ganhar afundando toda a frota. A célula inferior direita mostra um retorno ao jogador de 9,81% do dinheiro apostado com essa estratégia.
Análise de frota
| Bolas | Paga | Probabilidade | Retornar |
|---|---|---|---|
| 16 | 300 | 0,000000 | 0,000000 |
| 17 | 300 | 0,000000 | 0,000000 |
| 18 | 300 | 0,000000 | 0,000000 |
| 19 | 300 | 0,000000 | 0,000000 |
| 20 | 300 | 0,000000 | 0,000000 |
| 21 | 300 | 0,000000 | 0,000000 |
| 22 | 300 | 0,000000 | 0,000000 |
| 23 | 300 | 0,000000 | 0,000000 |
| 24 | 300 | 0,000000 | 0,000000 |
| 25 | 300 | 0,000000 | 0,000000 |
| 26 | 300 | 0,000000 | 0,000000 |
| 27 | 300 | 0,000000 | 0,000000 |
| 28 | 300 | 0,000000 | 0,000000 |
| 29 | 300 | 0,000000 | 0,000000 |
| 30 | 300 | 0,000000 | 0,000000 |
| 31 | 300 | 0,000000 | 0,000000 |
| 32 | 300 | 0,000000 | 0,000000 |
| 33 | 300 | 0,000000 | 0,000001 |
| 34 | 300 | 0,000000 | 0,000001 |
| 35 | 300 | 0,000000 | 0,000003 |
| 36 | 300 | 0,000000 | 0,000005 |
| 37 | 300 | 0,000000 | 0,000008 |
| 38 | 300 | 0,000000 | 0,000013 |
| 39 | 300 | 0,000000 | 0,000022 |
| 40 | 300 | 0,000000 | 0,000035 |
| 41 | 300 | 0,000000 | 0,000056 |
| 42 | 300 | 0,000001 | 0,000089 |
| 43 | 300 | 0,000001 | 0,000138 |
| 44 | 300 | 0,000002 | 0,000212 |
| 45 | 300 | 0,000003 | 0,000321 |
| 46 | 300 | 0,000005 | 0,000482 |
| 47 | 300 | 0,000007 | 0,000715 |
| 48 | 300 | 0,000011 | 0,001050 |
| 49 | 300 | 0,000016 | 0,001528 |
| 50 | 300 | 0,000023 | 0,002202 |
| 51 | 100 | 0,000033 | 0,001049 |
| 52 | 100 | 0,000048 | 0,001485 |
| 53 | 100 | 0,000069 | 0,002088 |
| 54 | 100 | 0,000098 | 0,002912 |
| 55 | 100 | 0,000139 | 0,004032 |
| 56 | 40 | 0,000194 | 0,002217 |
| 57 | 40 | 0,000270 | 0,003029 |
| 58 | 40 | 0,000372 | 0,004110 |
| 59 | 40 | 0,000511 | 0,005544 |
| 60 | 40 | 0,000697 | 0.007434 |
| 61 | 10 | 0,000945 | 0,002478 |
| 62 | 10 | 0,001273 | 0,003286 |
| 63 | 10 | 0,001707 | 0,004335 |
| 64 | 10 | 0,002276 | 0,005689 |
| 65 | 10 | 0,003019 | 0,007431 |
| 66 | 4 | 0,003985 | 0,003864 |
| 67 | 4 | 0,005235 | 0,005001 |
| 68 | 4 | 0,006846 | 0,006443 |
| 69 | 4 | 0,008912 | 0,008267 |
| 70 | 4 | 0,011553 | 0,010563 |
| 71+ | 0 | 0,988447 | 0,000000 |
| Total | 1.000000 | 0,098136 |
Análise da Frota de Bônus
A tabela a seguir mostra minha análise de como ganhar afundando toda a frota, menos um quadrado. Em outras palavras, 15 dos 16 números cobertos por navios. A célula inferior direita mostra um retorno ao jogador de 14,79% do dinheiro apostado com essa estratégia.
Análise da Frota de Bônus
| Bolas | Paga | Probabilidade | Retornar |
|---|---|---|---|
| 15 | 40 | 0,000000 | 0,000000 |
| 16 | 40 | 0,000000 | 0,000000 |
| 17 | 40 | 0,000000 | 0,000000 |
| 18 | 40 | 0,000000 | 0,000000 |
| 19 | 40 | 0,000000 | 0,000000 |
| 20 | 40 | 0,000000 | 0,000000 |
| 21 | 40 | 0,000000 | 0,000000 |
| 22 | 40 | 0,000000 | 0,000000 |
| 23 | 40 | 0,000000 | 0,000000 |
| 24 | 40 | 0,000000 | 0,000000 |
| 25 | 40 | 0,000000 | 0,000000 |
| 26 | 40 | 0,000000 | 0,000000 |
| 27 | 40 | 0,000000 | 0,000000 |
| 28 | 40 | 0,000000 | 0,000000 |
| 29 | 40 | 0,000000 | 0,000000 |
| 30 | 40 | 0,000000 | 0,000001 |
| 31 | 40 | 0,000000 | 0,000002 |
| 32 | 40 | 0,000000 | 0,000003 |
| 33 | 40 | 0,000000 | 0,000005 |
| 34 | 40 | 0,000000 | 0,000009 |
| 35 | 40 | 0,000000 | 0,000014 |
| 36 | 40 | 0,000001 | 0,000023 |
| 37 | 40 | 0,000001 | 0,000037 |
| 38 | 40 | 0,000001 | 0,000059 |
| 39 | 40 | 0,000002 | 0,000092 |
| 40 | 40 | 0,000004 | 0,000141 |
| 41 | 40 | 0,000005 | 0,000212 |
| 42 | 40 | 0,000008 | 0,000315 |
| 43 | 40 | 0,000012 | 0,000463 |
| 44 | 40 | 0,000017 | 0,000672 |
| 45 | 40 | 0,000024 | 0,000964 |
| 46 | 40 | 0,000034 | 0,001368 |
| 47 | 40 | 0,000048 | 0,001922 |
| 48 | 40 | 0,000067 | 0,002674 |
| 49 | 40 | 0,000092 | 0,003685 |
| 50 | 40 | 0,000126 | 0,005033 |
| 51 | 10 | 0,000170 | 0,001704 |
| 52 | 10 | 0,000229 | 0,002288 |
| 53 | 10 | 0,000305 | 0,003049 |
| 54 | 10 | 0,000403 | 0,004032 |
| 55 | 10 | 0,000529 | 0,005291 |
| 56 | 4 | 0,000690 | 0,002758 |
| 57 | 4 | 0,000892 | 0,003569 |
| 58 | 4 | 0,001147 | 0,004588 |
| 59 | 4 | 0,001465 | 0.005859 |
| 60 | 4 | 0,001858 | 0,007434 |
| 61 | 2 | 0,002343 | 0,004687 |
| 62 | 2 | 0,002936 | 0,005873 |
| 63 | 2 | 0,003657 | 0,007315 |
| 64 | 2 | 0,004528 | 0,009057 |
| 65 | 2 | 0,005573 | 0,011146 |
| 66 | 1 | 0,006819 | 0,006819 |
| 67 | 1 | 0,008294 | 0,008294 |
| 68 | 1 | 0,010029 | 0,010029 |
| 69 | 1 | 0,012055 | 0,012055 |
| 70 | 1 | 0,014404 | 0,014404 |
| 71+ | 0 | 0,921228 | 0,000000 |
| Total | 1.000000 | 0,147946 |
Resumo
A tabela a seguir mostra a contribuição de todos os elementos do jogo para o retorno. A célula inferior direita mostra um retorno total de 74,25%. Para confirmar isso, joguei 900 partidas, que apresentaram um retorno geral de 71,63%. Acho que nunca ganhei o prêmio principal nessas 900 partidas. Se você subtrair os 2,47% do retorno referentes a não ter ganhado o prêmio principal, você obtém 71,78%, o que é próximo do meu retorno de 71,63% nas 900 partidas.
Resumo
| Maneira de Vencer | Retornar |
|---|---|
| Prêmio principal | 2,47% |
| Escalão | 8,22% |
| Divisão | 13,67% |
| Brigada | 13,19% |
| Esquadrão | 12,10% |
| Frota | 9,81% |
| Frota de bônus | 14,79% |
| Total | 74,25% |
Vídeo
Neste vídeo, demonstro as regras do jogo Batalha Naval.