Nesta página
Probabilidades do Bingo: Análise do jackpot progressivo Jumbo nos Cassinos Station
Nesta página
Atualizar
Desde que escrevi meu relatório inicial, os cassinos Station evidentemente mudaram a distribuição de cartas pares e ímpares novamente, provavelmente em algum momento de outubro. A tabela a seguir mostra uma distribuição recente de cartas que eu e outro jogador, que chamarei de "L", pegamos.
 Ohio Salas de bingo online recomendadas
Ohio Salas de bingo online recomendadas
Nova amostra de cartelas de bingo gigantes
| Número de probabilidades | Amostra de Mike | Amostra de L | Amostra Total | Probabilidade |
|---|---|---|---|---|
| 9 | 2 | 3 | 5 | 0,011261 |
| 10 | 7 | 10 | 17 | 0,038288 |
| 11 | 14 | 25 | 39 | 0,087838 |
| 12 | 34 | 41 | 75 | 0,168919 |
| 13 | 41 | 71 | 112 | 0,252252 |
| 14 | 86 | 110 | 196 | 0,441441 |
| Total | 184 | 260 | 444 | 1 |
Embora a variação de probabilidades de 9 a 14 permaneça a mesma, a probabilidade agora está fortemente concentrada na probabilidade de 14, em vez da distribuição mais equilibrada anterior. Maior probabilidade torna mais difícil ganhar o jackpot progressivo. Com base nesta amostragem, agora recomendo esperar até que a Jumbo Ball atinja 54 se você quiser um valor esperado positivo.
A próxima tabela compara minha amostra total com os totais esperados, considerando o mesmo tamanho de amostra e a probabilidade de cada total, assumindo o mesmo método de sorteio de cartas que me foi explicado anteriormente por Stephen L. Cavallaro (Vice-Presidente Executivo e Diretor de Operações da Station Casinos).
Totais reais versus totais esperados
| Número de probabilidades | Total da amostra | Total esperado |
|---|---|---|
| 9 | 5 | 33,17 |
| 10 | 17 | 60,48 |
| 11 | 39 | 87,61 |
| 12 | 75 | 101,15 |
| 13 | 112 | 93,18 |
| 14 | 196 | 68,41 |
| Total | 444 | 444 |
É evidente que meus resultados não estão de acordo com o esperado. Um teste estatístico de assimetria desta distribuição, comparado às expectativas, resulta em um valor qui-quadrado de 330,71 com 5 graus de liberdade. A probabilidade de resultados com essa assimetria ou maior é de 1 em 402.433.741.048.496.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000. Para se ter uma ideia, a probabilidade de acertar a Powerball oito vezes seguidas é maior.
Para reforçar o argumento de que houve uma mudança na forma como as cartas são sorteadas, a tabela a seguir mostra os resultados da minha amostra antes e depois da suposta alteração. A amostra 1 foi coletada em agosto, e a amostra 2, em 30 de outubro e 1º de novembro.
Amostra antiga vs. nova
| Número de probabilidades | Amostra 1 | Amostra 2 | Probabilidade da Amostra 1 | Probabilidade da Amostra 2 |
|---|---|---|---|---|
| 9 | 35 | 5 | 13,51% | 1,13% |
| 10 | 35 | 17 | 13,51% | 3,83% |
| 11 | 34 | 39 | 13,13% | 8,78% |
| 12 | 48 | 75 | 18,53% | 16,89% |
| 13 | 55 | 112 | 21,24% | 25,23% |
| 14 | 52 | 196 | 20,08% | 44,14% |
| Total | 259 | 444 | 100% | 100% |
O gráfico a seguir compara as duas colunas de probabilidade na tabela acima em relação às probabilidades esperadas.
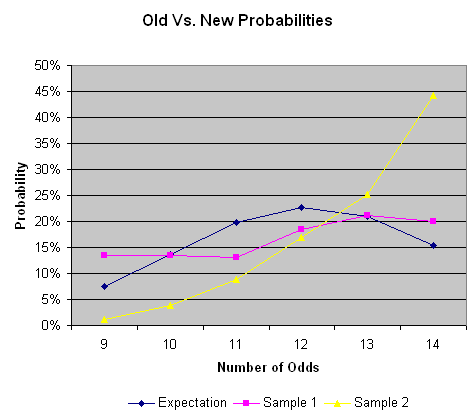
Questionei a gerência do Station Casinos sobre como os novos baralhos são sorteados e me disseram que não houve nenhuma mudança. Não houve qualquer comentário sobre as minhas evidências em contrário e, devido à minha "reportagem negativa", negaram-me qualquer cooperação adicional.
Observações: A amostra de "Mike" foi coletada na sessão das 15h do dia 1º de novembro, na Estação Sunset. A amostra de "L" foi coletada nas sessões das 9h e das 11h do dia 30 de outubro, na Estação Boulder.
Segue abaixo meu estudo inicial, que agora está desatualizado.
Segue abaixo a minha evidência de que as cartelas de bingo progressivo vendidas nos cassinos de Las Vegas listados abaixo não são criadas de forma totalmente aleatória.
- Estação Palace
- Estação Santa Fé
- Estação do Texas
- Estação Boulder
- Estação do Pôr do Sol
- Fiesta Rancho
- Festa Henderson
- Cidade de Sam
Os cassinos Station em Las Vegas oferecem um bingo progressivo interligado chamado Jumbo Bingo. O prêmio inicial é de US$ 100.000. Para ganhar, o jogador precisa completar uma cartela (preencher todos os 24 números) em até 47 chamadas. Caso ninguém em nenhuma das cinco salas de bingo consiga completar a cartela na primeira semana, o número de chamadas necessárias para ganhar o prêmio (chamado de Jumbo Ball) aumenta em um, para 48. Da mesma forma, o valor do Jumbo Ball aumentará em um a cada semana até que alguém ganhe.
Evidentemente, para economizar tempo, os primeiros 37 números sorteados são todos pares, entre 2 e 74. As cartelas do Jumbo Bingo já vêm pré-marcadas com todos os números pares. Quando o jogo começa, o locutor pergunta se alguém ganhou com base em uma cartela com todos os números pares. Depois que ninguém reivindicar uma cartela premiada, o locutor sorteará bolas aleatoriamente, desconsiderando as bolas com números pares. Se ninguém completar a cartela até o sorteio da Jumbo Ball, haverá um prêmio de consolação de US$ 5.000 para quem completar a cartela em até 52 sorteios. Se ninguém reivindicar a vitória, haverá um prêmio de US$ 1.199 para a primeira pessoa a completar a cartela, independentemente do número de sorteios. Como sempre no bingo, qualquer prêmio será dividido se vários jogadores ganharem simultaneamente.
Os cassinos Fiesta têm um jogo muito semelhante, porém em menor escala. O prêmio principal começa em US$ 25.000 e os prêmios de consolação são menores. A regra é a mesma: todos os números pares são sorteados antecipadamente. No Sam's Town, o jogo é invertido, com os números ímpares sendo sorteados antecipadamente.
A tabela a seguir exibe a distribuição de probabilidade de acordo com o total de números ímpares no cartão para um cartão justo. Minha definição de um cartão justo é aquele em que os 5 números "B" são escolhidos aleatoriamente de 1 a 15, os 5 números "I" são escolhidos aleatoriamente entre 16 e 30, e assim por diante. Outra maneira de obter o mesmo resultado seria sortear números de 1 a 75, preenchendo o cartão à medida que os números são escolhidos e descartando os números se a coluna correspondente já estiver preenchida.
Probabilidade para o Total de Números Ímpares - Fair Card
| Número de probabilidades | Probabilidade | Probabilidade inversa |
|---|---|---|
| 0 | 0,000000000436 | 1 em 2293355030 |
| 1 | 0,000000022747 | 1 em 43962077 |
| 2 | 0,000000534794 | 1 em 1869877 |
| 3 | 0,000007530006 | 1 em 132802 |
| 4 | 0,000071202834 | 1 em 14044 |
| 5 | 0,000480801205 | 1 em 2080 |
| 6 | 0,002407676276 | 1 em 415 |
| 7 | 0,00916827051 | 1 em 109 |
| 8 | 0,027013789916 | 1 em 37 |
| 9 | 0,062346657338 | 1 em 16 |
| 10 | 0,113677702037 | 1 em 9 |
| 11 | 0.164671200005 | 1 em 6 |
| 12 | 0,1901222602 | 1 em 5 |
| 13 | 0,175132872532 | 1 em 6 |
| 14 | 0,1285740634 | 1 em 8 |
| 15 | 0,074984221403 | 1 em 13 |
| 16 | 0,034540809008 | 1 em 29 |
| 17 | 0,012458867878 | 1 em 80 |
| 18 | 0,003475365511 | 1 em 288 |
| 19 | 0,00073657509 | 1 em 1358 |
| 20 | 0,000115624911 | 1 em 8649 |
| 21 | 0,000012937867 | 1 em 77292 |
| 22 | 0,000000969822 | 1 em 1031117 |
| 23 | 0,000000043401 | 1 em 23041075 |
| 24 | 0,000000000872 | 1 em 1146677515 |
| Total | 1 | 1 em 1 |
Obviamente, uma cartela com poucas probabilidades teria uma boa vantagem inicial e uma chance muito maior de ganhar do que uma cartela com a maioria dos números ímpares. Na edição de julho de 2002 do Las Vegas Advisor, escrevi um artigo sobre o Jumbo Bingo, partindo do pressuposto de que as cartelas eram criadas aleatoriamente. Um leitor daquela coluna me disse acreditar que as cartelas não eram criadas aleatoriamente, com base no fato de que ele comprou 1500 cartelas e todas elas tinham um total de probabilidades entre 9 e 14.
Para confirmar a acusação de que todas as cartelas tinham probabilidades de 9 a 14, meu assistente, Rob Feldheim, reuniu 259 cartelas de bingo Jumbo na estação Palace. Em seguida, contamos o número de probabilidades em cada cartela e, como eu temia, o total de probabilidades era sempre de 9 a 14. A tabela a seguir mostra o total para cada número de probabilidades e o total esperado em um jogo justo.
Cartões da estação Palace: comparação entre o valor real e o esperado.
| Número de probabilidades | Número na amostra | Esperado Total |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0,000006 |
| 2 | 0 | 0,000139 |
| 3 | 0 | 0,00195 |
| 4 | 0 | 0,018442 |
| 5 | 0 | 0,124528 |
| 6 | 0 | 0,623588 |
| 7 | 0 | 2,374582 |
| 8 | 0 | 6,996572 |
| 9 | 35 | 16,147784 |
| 10 | 35 | 29,442525 |
| 11 | 34 | 42,649841 |
| 12 | 48 | 49,241665 |
| 13 | 55 | 45.359414 |
| 14 | 52 | 33.300682 |
| 15 | 0 | 19.420913 |
| 16 | 0 | 8,94607 |
| 17 | 0 | 3,226847 |
| 18 | 0 | 0,90012 |
| 19 | 0 | 0,190773 |
| 20 | 0 | 0,029947 |
| 21 | 0 | 0,003351 |
| 22 | 0 | 0,000251 |
| 23 | 0 | 0,000011 |
| 24 | 0 | 0 |
| Total | 259 | 259 |
A probabilidade de o número total de probabilidades estar entre 9 e 14 é de 0,834524756. Da amostra de 42,858088 probabilidades, nenhuma deveria estar fora do intervalo de 9 a 14. A probabilidade de isso acontecer em um jogo justo é de 0,834524756 / 259 = 4,4953 * 10⁻²¹ , ou 1 em 222.454.364.282.805.000.000.
Aqui estão os resultados do mesmo tipo de teste realizado em cartelas de bingo Grande obtidas após a sessão das 11h do dia 22 de agosto de 2002, no Fiesta Rancho.
Cartões Fiesta Rancho, comparação entre o valor real e o esperado.
| Número de probabilidades | Número na amostra | Esperado Total |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0,000002 |
| 2 | 0 | 0,000047 |
| 3 | 0 | 0,000655 |
| 4 | 0 | 0,006195 |
| 5 | 0 | 0,04183 |
| 6 | 0 | 0,209468 |
| 7 | 0 | 0,79764 |
| 8 | 0 | 2,3502 |
| 9 | 10 | 5,424159 |
| 10 | 6 | 9,88996 |
| 11 | 19 | 14,326394 |
| 12 | 18 | 16,540637 |
| 13 | 18 | 15,23656 |
| 14 | 16 | 11.185944 |
| 15 | 0 | 6,523627 |
| 16 | 0 | 3.00505 |
| 17 | 0 | 1,083922 |
| 18 | 0 | 0,302357 |
| 19 | 0 | 0,064082 |
| 20 | 0 | 0,010059 |
| 21 | 0 | 0,001126 |
| 22 | 0 | 0,000084 |
| 23 | 0 | 0,000004 |
| 24 | 0 | 0 |
| Total | 87 | 87 |
A seguir, apresento o resultado da minha amostra de cartões progressivos da Sams Town.
Cartões da Sam's Town: reais vs. esperados
| Número de pares | Número na amostra | Esperado Total |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0,000002 |
| 2 | 0 | 0,000055 |
| 3 | 0 | 0,000768 |
| 4 | 0 | 0,007263 |
| 5 | 0 | 0,049042 |
| 6 | 0 | 0,245583 |
| 7 | 0 | 0,935164 |
| 8 | 1 | 2,755407 |
| 9 | 1 | 6,359359 |
| 10 | 19 | 11,595126 |
| 11 | 25 | 16,796462 |
| 12 | 24 | 19,392471 |
| 13 | 20 | 17,863553 |
| 14 | 12 | 13.114554 |
| 15 | 0 | 7,648391 |
| 16 | 0 | 3,523163 |
| 17 | 0 | 1,270805 |
| 18 | 0 | 0,354487 |
| 19 | 0 | 0,075131 |
| 20 | 0 | 0,011794 |
| 21 | 0 | 0,00132 |
| 22 | 0 | 0,000099 |
| 23 | 0 | 0,000004 |
| 24 | 0 | 0 |
| Total | 102 | 102 |
Eu esperava obter uma variedade de 10 a 15 cartas ímpares, ou de 9 a 14 cartas pares, no Sam's Town, com base em uma conversa com Stephen L. Cavallaro, da Station Casinos. No entanto, recebi uma carta com 8 cartas pares e apenas uma com 9. A probabilidade de qualquer carta ter de 8 a 14 cartas pares é de 0,881703. A probabilidade de 102 cartas estarem nessa faixa é de 2,647786 * 10⁻⁶ , ou 1 em 377.674.
Além disso, realizei um teste semelhante em cartelas de bingo comuns da Suncoast. Uma amostra de 129 cartelas apresentou os seguintes resultados reais e esperados.
Cartões Suncoast, comparação entre o valor real e o esperado.
| Número de probabilidades | Número na amostra | Esperado Total |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0,000003 |
| 2 | 0 | 0,000069 |
| 3 | 0 | 0,000971 |
| 4 | 0 | 0,009185 |
| 5 | 0 | 0,062023 |
| 6 | 0 | 0,31059 |
| 7 | 1 | 1,182707 |
| 8 | 6 | 3,484779 |
| 9 | 5 | 8.042719 |
| 10 | 17 | 14,664424 |
| 11 | 19 | 21,242585 |
| 12 | 29 | 24,525772 |
| 13 | 20 | 22,592141 |
| 14 | 18 | 16,586054 |
| 15 | 10 | 9,672965 |
| 16 | 1 | 4,455764 |
| 17 | 3 | 1,607194 |
| 18 | 2 | 0,448322 |
| 19 | 0 | 0,095018 |
| 20 | 0 | 0,014916 |
| 21 | 0 | 0,001669 |
| 22 | 0 | 0,000125 |
| 23 | 0 | 0,000006 |
| 24 | 0 | 0 |
| Total | 129 | 129 |
Das 129 cartas, 21 estavam fora do intervalo de 9 a 14, sendo o número esperado 21,34630654. Essas cartas passaram facilmente no teste de par/ímpar. E deveriam ter passado, já que não havia nenhum jogo em que os números pares ou ímpares fossem anunciados com antecedência.
A próxima tabela mostra a probabilidade de ganhar em um jogo justo, assumindo que o jogador deve acertar todos os números dentro de um intervalo de 50.
Probabilidade de ganhar - Carta justa
| Número de probabilidades | Probabilidade de Cartão | Probabilidade Vitórias de cartas | Total Probabilidade |
|---|---|---|---|
| 0 | 0,000000000436 | 1 | 0,000000000436 |
| 1 | 0,000000022747 | 0,342105263158 | 0,000000007782 |
| 2 | 0,000000534794 | 0,110953058321 | 0,000000059337 |
| 3 | 0,000007530006 | 0,033902323376 | 0,000000255285 |
| 4 | 0,000071202834 | 0,009686378107 | 0,000000689698 |
| 5 | 0,000480801205 | 0,002564041264 | 0,000001232794 |
| 6 | 0,002407676276 | 0,000621585761 | 0,000001496577 |
| 7 | 0,00916827051 | 0,000135971885 | 0,000001246627 |
| 8 | 0,027013789916 | 0,000026317139 | 0,000000710926 |
| 9 | 0,062346657338 | 0,00000438619 | 0,000000273464 |
| 10 | 0,113677702037 | 0,000000604992 | 0,000000068774 |
| 11 | 0,164671200005 | 0,000000064821 | 0,000000010674 |
| 12 | 0,1901222602 | 0,000000004802 | 0,000000000913 |
| 13 | 0,175132872532 | 0,000000000185 | 0,000000000032 |
| 14 | 0,1285740634 | 0 | 0 |
| 15 | 0,074984221403 | 0 | 0 |
| 16 | 0,034540809008 | 0 | 0 |
| 17 | 0,012458867878 | 0 | 0 |
| 18 | 0,003475365511 | 0 | 0 |
| 19 | 0,00073657509 | 0 | 0 |
| 20 | 0,000115624911 | 0 | 0 |
| 21 | 0,000012937867 | 0 | 0 |
| 22 | 0,000000969822 | 0 | 0 |
| 23 | 0,000000043401 | 0 | 0 |
| 24 | 0,000000000872 | 0 | 0 |
| Total | 1 | 0 | 0,000006053319 |
A imagem inferior à direita mostra que a probabilidade geral de ganhar é de 0,000006053319, ou 1 em 165199. Se houver uma vitória em um jogo justo, observe que é mais provável que ela ocorra com uma carta de valor 6. A probabilidade de uma carta vencedora em um jogo justo ter menos de 9 valores é de 94,15%.
Quando souberam que eu planejava escrever sobre minha investigação, fui convidado a me encontrar com Stephen L. Cavallaro (Vice-Presidente Executivo e Diretor de Operações da Station Casinos) e Jonathan Swain (Vice-Presidente e Gerente Geral do Palace Station). Stephen admitiu abertamente que as cartelas foram pré-selecionadas para conter probabilidades de 9 a 14 cada. Ele disse que isso visava equilibrar o jogo e dar a cada cartela e cliente a esperança de ganhar. Ele também disse que, inicialmente, a variação era muito maior e que o primeiro vencedor tinha apenas 3 probabilidades na cartela. Além disso, ele afirmou que o Sam's Town e o Fiesta Casinos faziam o mesmo e que o jogo da Station era totalmente aprovado pelo Conselho de Controle de Jogos de Nevada.
Em uma ligação telefônica posterior, Stephen Cavallaro me disse que o processo de criação dos cartões é o seguinte: o computador escolhe aleatoriamente um conjunto de números justos. Se a soma das probabilidades estiver entre 9 e 14, o cartão é impresso; caso contrário, o conjunto de números é descartado e o próximo conjunto é gerado. A tabela a seguir mostra a probabilidade ajustada para cada número de probabilidades de acordo com esse método de criação de cartões.
Probabilidade para Total de Números Ímpares - Cartão da Estação
| Número de probabilidades | Probabilidade |
|---|---|
| 9 | 0,074709 |
| 10 | 0,136218 |
| 11 | 0,197323 |
| 12 | 0,227821 |
| 13 | 0,209859 |
| 14 | 0,154069 |
| Total | 1 |
De modo geral, o resultado da remoção das melhores cartas do sorteio é que a probabilidade de qualquer carta acertar o prêmio progressivo é substancialmente menor. Remover as piores cartas não compensa essa redução. Essa política de pré-seleção de cartas resulta em jackpots cada vez maiores. Ao mesmo tempo, os cassinos precisam reabastecer o medidor com menos frequência. O resultado final é um número menor de vencedores de jackpots progressivos e um total de prêmios menores. A próxima tabela mostra a probabilidade esperada de uma carta justa e de uma carta Stations ganharem, de acordo com o número de bolas sorteadas para ganhar o jackpot.
Probabilidade esperada de ganhar
| Número de Chamadas | Cartão Justo | Cartão de Estações | Razão |
|---|---|---|---|
| 47 | 1 em 1.122.373 | 1 em 205.287.873 | 182,91 |
| 48 | 1 em 583.217 | 1 em 35.037.983 | 60,08 |
| 49 | 1 em 308.005 | 1 em 8.203.638 | 26,63 |
| 50 | 1 em 165.199 | 1 em 2.358.363 | 14,28 |
| 51 | 1 em 89.925 | 1 em 785.008 | 8,73 |
| 52 | 1 em 49.648 | 1 em 291.923 | 5,88 |
| 53 | 1 em 27.784 | 1 em 118.433 | 4,26 |
A coluna de proporção mostra quantas vezes mais difícil é ganhar usando um cartão de cassino Station em comparação com um cartão justo. Por exemplo, é 14,28 vezes mais difícil ganhar se o prêmio principal precisar ser acertado em 50 bolas ou menos.
Na minha opinião, todas as cartelas de bingo deveriam ser criadas de forma verdadeiramente aleatória, conforme sugerido acima. Caso contrário, acredito que, se uma cartela não for criada aleatoriamente, as regras sobre a forma como ela é criada e o efeito sobre o jogador deveriam ser divulgadas. Em todas as formas de jogos de azar, defendo veementemente a justiça e a transparência. Não vejo nenhuma dessas duas coisas acontecendo no bingo no estado de Nevada. Portanto, que o jogador de bingo fique atento.
Agradeço a Stephen Cavallaro e Jonathan Swaim por se reunirem comigo e pela transparência demonstrada sobre este assunto.
Voltar às probabilidades no bingo Michael Shackleford, ASA
 Ohio Cassinos online recomendados
Ohio Cassinos online recomendados
Ver tudo
BÔNUS DE ATÉ $11.000
Jogadores de todos os EUA são bem-vindos.
Mais de 200 jogos de cassino
Jogue no PC ou no celular
BÔNUS DE ATÉ $3000
Cassino e apostas esportivas
Apenas jogadores americanos
Jogue no computador ou no celular.
$7777 + 300 Giros Grátis
Jogos com crupiê ao vivo
Torneios diários gratuitos
Compatível com dispositivos móveis e computadores.
Outras páginas de bingo
- Minha página geral de bingo
- Prêmios acumulados do Palace Station Cash Ball em 2007 .
- Prêmios acumulados do Cash Ball da Boulder Station em 2007
- Prêmios acumulados do Cash Ball do Fiesta Henderson em 2007
- Prêmios acumulados do Cash Ball da Texas Station em 2007
- Prêmios acumulados do Sunset Station Cash Ball em 2007
- Prêmios acumulados do Cash Ball da Estação Santa Fé em 2007
- Prêmios acumulados do Red Rock Cash Ball em 2007
- Prêmios acumulados do Cash Ball dos cassinos Coast em 2007






