Nesta página
Ferrovia
Introdução
Chemin de Fer é um precursor antiquado do bacará moderno. Provavelmente não mereceria muita discussão como um jogo extinto, não fosse o fato de ser muito apreciado por James Bond, e de vez em quando me perguntam exatamente o que Bond estava jogando. Acredito que o jogo finalmente desapareceu, como o dodô, na década de 1990. Mesmo assim, merece um capítulo de destaque na história dos jogos de azar, e fico feliz em ajudar a escrevê-lo.
Regras
Para evitar confusão, ao me referir às mãos do Jogador e do Banqueiro, usarei letras maiúsculas e geralmente direi "Mão do Jogador" ou "Mão do Banqueiro". Ao me referir a um jogador ou banqueiro humano, usarei letras minúsculas. Primeiro, explicarei as regras de pontuação, que são as mesmas do bacará, e depois as regras de procedimento. Se você já está familiarizado com o bacará, pode pular a parte das regras de pontuação.
As fontes divergem em relação a algumas regras. Limitarei minha análise a duas fontes. Outras fontes parecem copiar de uma dessas fontes ou de outra.
- O Novo Guia Completo de Jogos de Azar de Scarne (copyright 1974) por John Scarne.
- Casino Royale (direitos autorais de 1953) por Ian Fleming.
As regras de pontuação de Scarne são as seguintes.
- São utilizados seis (Fleming) ou oito (Scarne) baralhos.
- As cartas recebem valores em pontos da seguinte forma: Ás = 1, 2-9 = valor numérico, 10 e figuras = 0.
- Existem duas mãos, conhecidas como Jogador e Banqueiro.
- Após todas as apostas serem feitas, o crupiê distribui duas cartas viradas para baixo para as mãos do Jogador e do Banqueiro.
- Para calcular os pontos por mão, some os pontos de cada carta individual na mão. Se a soma for maior que 9, descarte o primeiro dígito. Por exemplo, se uma das mãos tiver um 9 e um 7, você descartaria o 1 do total de 16, resultando em uma mão de 6 pontos.
- A mão com o maior número de pontos vence.
- Se qualquer uma das mãos de duas cartas tiver 8 ou 9 pontos, nenhum dos lados poderá comprar mais cartas.
- Caso contrário, o jogador que atua em nome da Mão do Jogador deverá agir da seguinte forma, com base no valor em pontos dessa mão.
- 0 a 4 pontos — Empate
- 5 pontos — O jogador tem a opção de empatar ou permanecer inativo.
- 6 ou 7 pontos — Fique em pé
- Se o jogador comprar uma carta, essa terceira carta será distribuída com a face para cima.
- Caso nenhuma terceira carta tenha sido distribuída para a mão do Jogador, a mão do Banqueiro deverá agir da seguinte forma, com base no valor em pontos da mão do Banqueiro.
- 0 a 5 pontos — Empate
- 6 ou 7 pontos — Fique em pé
- Se uma terceira carta for comprada para a mão do Jogador, o Banqueiro deverá decidir se compra ou mantém a mão, de acordo com o valor em pontos de sua mão de duas cartas e da carta comprada para a mão do Jogador, conforme mostrado na tabela abaixo.
- Os valores finais dos pontos das mãos do Jogador e do Banqueiro são comparados. Se a mão do Jogador vencer, as apostas são pagas com o valor apostado. Em caso de empate, é considerado um "push" (empate). Se a mão do Banqueiro vencer, as apostas são perdidas.
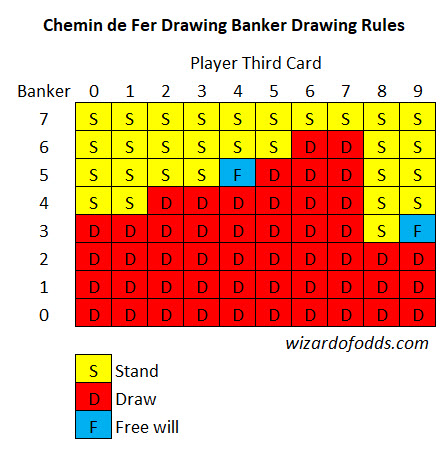
A diferença entre as regras de Fleming e as de Fleming reside no fato de que ambas as partes tinham livre arbítrio, exceto quando uma delas tinha um natural. No entanto, Fleming parece indicar que havia uma maneira bastante rígida de jogar, onde o protocolo ditava como jogar a maioria das mãos, deixando poucas possibilidades para o livre arbítrio.
As regras processuais são as seguintes.
- Diferentemente do bacará, o chemin de fer é um jogo em que o jogador tem a banca como principal aliada.
- O papel do cassino é distribuir as cartas e arbitrar o jogo, não honrar as apostas.
- Um jogador será designado para jogar a mão do banqueiro e honrar todas as apostas na mão do jogador.
- Se a mão do banqueiro venceu ou empatou na rodada anterior, a mesma pessoa pode continuar atuando como banqueiro, desde que esteja disposta a apostar pelo menos o mesmo valor da mão anterior. A alternativa é desistir do baralho.
- Se o jogador que atuou como banqueiro perdeu a mão anterior, ele deve descartar as cartas do baralho. O próximo jogador na mesa, no sentido anti-horário, tem a opção de se tornar o banqueiro, desde que esteja disposto a apostar pelo menos o mesmo valor apostado na mão anterior pelo banqueiro anterior.
- Se ninguém estiver disposto a apostar o valor necessário na mão do banqueiro, a opção de ser o banqueiro passa para o jogador que estiver disposto a apostar mais. Em caso de empate, a opção passa para o jogador mais próximo do banqueiro anterior, seguindo no sentido anti-horário ao redor da mesa.
- Independentemente de quem estiver bancando e por quê, o banqueiro tem a opção de aumentar o valor que está disposto a apostar, até o dobro do valor apostado na mão anterior.
- Uma vez definido o banqueiro e a aposta máxima na mão do banqueiro, podem ser feitas apostas na mão do jogador.
- Qualquer jogador que esteja disposto a apostar o valor total da aposta do banqueiro tem prioridade para fazê-lo.
- Se mais de um jogador estiver disposto a apostar o valor máximo, a primeira opção será dada ao jogador que apostou o valor máximo na mão anterior e perdeu. Isso é conhecido como "suive", que significa "seguir" em francês.
- Caso contrário, a opção de fazer uma aposta máxima é oferecida ao redor da mesa, começando pelo jogador à direita do banqueiro e seguindo no sentido anti-horário.
- Se ninguém optar por apostar o valor total da aposta do banqueiro, o jogador à direita do banqueiro poderá apostar o quanto quiser, até o limite da aposta do banqueiro.
- As apostas continuam ao redor da mesa, no sentido anti-horário, até que as apostas na Mão do Jogador sejam iguais à aposta no Banqueiro.
- Após todas as apostas serem concluídas, duas cartas serão distribuídas para as mãos do Jogador e do Banqueiro, com a face para baixo.
- O jogador que apostar a maior quantia na Mão do Jogador receberá as cartas e terá autoridade para tomar qualquer decisão.
- Se a mão do jogador, composta por duas cartas, tiver oito ou nove pontos, ela deve ser revelada imediatamente.
- Se o jogador que estiver agindo na mão do jogador revelar uma mão de oito ou nove pontos (conhecida como "natural"), a mão do banqueiro também será revelada imediatamente, pois nenhum dos lados pode desistir.
- Caso contrário, após o jogador que estiver agindo com a mão do jogador tomar uma decisão de manter ou comprar, o banqueiro deverá revelar suas duas cartas.
- Se a mão de duas cartas do banqueiro totalizar oito ou nove pontos, nenhuma terceira carta será distribuída para a mão do jogador, pois não é possível receber mais cartas se qualquer um dos lados tiver uma mão de duas cartas com 8 ou 9 pontos.
- Caso contrário, se o jogador que estiver agindo com a mão do jogador comprar uma carta, ela será distribuída a ele com a face para cima.
- Após o jogador que atua como "Jogador" ter agido, assumindo que nenhum dos lados tenha uma mão natural de 8 ou 9 pontos, então o jogador que atua como banqueiro terá a sua vez.
- Se a mão do jogador não comprar uma terceira carta, o banqueiro deverá comprar com cinco pontos ou menos e parar com seis ou sete pontos.
- Caso contrário, se a mão do Jogador tiver comprado uma terceira carta, a mão do Banqueiro deverá usar a tabela nas Regras de Pontuação acima para determinar sua ação, de acordo com o total de pontos na mão de duas cartas do Banqueiro e na terceira carta comprada para a mão do Jogador.
- As mãos serão pontuadas e julgadas pela equipe do cassino.
- Segundo Scarne, se a mão do banqueiro ganhasse, a casa cobraria uma comissão, geralmente 5% do total das apostas dos jogadores, que o banqueiro deveria pagar. De acordo com Fleming, uma "pequena porcentagem" era cobrada de cada aposta. Aqui estão suas palavras exatas em Casino Royale (que foi baseado no jogo Chemin de Fer no livro): "De cada aposta, o cassino fica com uma pequena porcentagem, a cagnotte, mas é comum em jogos grandes que o banqueiro a contribua ele mesmo, seja em um montante pré-acordado ou por meio de contribuições ao final de cada mão, para que o valor da aposta do banco seja sempre um número redondo. Le Chiffre escolheu a segunda opção."
Análise das Regras de Scarne
Entre três situações de livre arbítrio no chemin de fer, existem 2*2*2 = 8 conjuntos de combinações de resultados para uma mão vencedora do Jogador, uma mão vencedora do Banqueiro e um empate. A tabela a seguir mostra essas combinações para todas as oito maneiras pelas quais os dois lados podem jogar suas mãos de livre arbítrio.
Combinações completas do jogo por estratégia
| Jogador 5 | Banqueiro 3 contra 9 | Banqueiro 5 contra.4 | Jogador | Banqueiro | Gravata |
|---|---|---|---|---|---|
| Ficar | Ficar | Ficar | 2.229.630.111.780.860 | 2.306.941.760.323.580 | 461.826.403.398.912 |
| Ficar | Ficar | Empate | 2.230.267.491.565.560 | 2.307.485.872.054.270 | 460.644.911.883.520 |
| Ficar | Empate | Ficar | 2.230.806.098.022.400 | 2.306.943.230.140.410 | 460.648.947.340.544 |
| Ficar | Empate | Empate | 2.231.443.477.807.100 | 2.307.487.341.871.100 | 459.467.455.825.152 |
| Empate | Ficar | Ficar | 2.230.565.660.708.860 | 2.290.372.874.305.530 | 477.459.740.488.960 |
| Empate | Ficar | Empate | 2.230.944.481.550.330 | 2.290.916.986.036.220 | 476.536.807.916.800 |
| Empate | Empate | Ficar | 2.230.139.461.750.780 | 2.291.708.454.707.200 | 476.550.359.045.376 |
| Empate | Empate | Empate | 2.230.518.282.592.250 | 2.292.252.566.437.880 | 475.627.426.473.216 |
A próxima tabela pega as combinações dos três resultados possíveis na tabela acima e as converte em probabilidades.
Probabilidades do Jogo Completo por Estratégia
| Jogador 5 | Banqueiro 3 contra 9 | Banqueiro 5 contra 4 | Jogador | Banqueiro | Gravata |
|---|---|---|---|---|---|
| Ficar | Ficar | Ficar | 0,446069 | 0,461536 | 0,092395 |
| Ficar | Ficar | Empate | 0,446196 | 0,461645 | 0,092159 |
| Ficar | Empate | Ficar | 0,446304 | 0,461536 | 0,092159 |
| Ficar | Empate | Empate | 0,446432 | 0,461645 | 0,091923 |
| Empate | Ficar | Ficar | 0,446256 | 0,458221 | 0,095523 |
| Empate | Ficar | Empate | 0,446332 | 0,458330 | 0,095338 |
| Empate | Empate | Ficar | 0,446171 | 0,458489 | 0,095341 |
| Empate | Empate | Empate | 0,446247 | 0,458597 | 0,095156 |
A próxima tabela mostra o valor esperado das apostas tanto na mão do jogador quanto na mão do banqueiro. O valor esperado da mão do banqueiro pressupõe uma comissão de 5% sobre os ganhos.
Valores esperados do jogo completo por estratégia
| Jogador 5 | Banqueiro 3 contra 9 | Banqueiro 5 contra 4 | Jogador | Banqueiro |
|---|---|---|---|---|
| Ficar | Ficar | Ficar | -0,015467 | -0,007610 |
| Ficar | Ficar | Empate | -0,015449 | -0,007634 |
| Ficar | Empate | Ficar | -0,015232 | -0,007845 |
| Ficar | Empate | Empate | -0,015214 | -0,007869 |
| Empate | Ficar | Ficar | -0,011965 | -0,010946 |
| Empate | Ficar | Empate | -0,011998 | -0,010918 |
| Empate | Empate | Ficar | -0,012318 | -0,010607 |
| Empate | Empate | Empate | -0,012351 | -0,010579 |
A tabela acima fornece orientações sobre a estratégia adequada. Primeiro, considere a decisão de "Parar" ou "Comprar" em uma mão do jogador com um total de cinco. Observe que, independentemente das quatro maneiras pelas quais o banqueiro possa jogar, o valor esperado na mão do jogador é significativamente maior ao pedir carta. O valor esperado médio ao parar é -0,015340 e ao pedir carta é -0,012158. Se o banqueiro aleatorizasse suas decisões, a vantagem da casa na aposta da mão do jogador seria 0,32% menor ao pedir carta do que ao parar.
Supondo que o jogador que age na Mão do Jogador vá comprar uma carta com um cinco, como o jogador que age na Mão do Banqueiro deve lidar com um total de cinco se a sua terceira carta for um 4? A tabela acima mostra que o valor esperado é 0,000028 maior ao comprar uma carta, independentemente de como uma Mão do Banqueiro 3 vs. 9 seja jogada.
Usando a mesma lógica, como o jogador que age na mão do banqueiro deve lidar com um total de três se a sua terceira carta for um 9? A tabela acima mostra que o valor esperado é 0,000339 maior ao comprar uma carta, independentemente de como uma mão do banqueiro com 5 ou 4 cartas seja jogada.
Em conclusão, nas três situações com livre arbítrio, o jogador que toma a decisão deve empatar.
Análise do Banqueiro 3 vs. 9
Embora eu já tenha argumentado que o valor esperado do jogo é maior na mão do banqueiro se ele tirar um 3 em vez de um 9, vamos analisar essa situação especificamente. As tabelas a seguir consideram apenas as mãos em que a mão do banqueiro tem um total de duas cartas igual a 3, a mão do jogador tirou um 9 e o jogador que age com a mão do jogador tira uma carta com um total de duas cartas igual a cinco.
A tabela a seguir mostra os possíveis resultados se o banqueiro parar em um 3 em vez de um 9. O valor esperado de parar é 0,457205 - 0,390567 = 0,043777.
Posição no banqueiro 3 contra 9
| Mão vencedora | Combinações | Probabilidade |
|---|---|---|
| Banqueiro | 10.382.475.829.248 | 0,457205 |
| Jogador | 8.869.227.331.584 | 0,390567 |
| Gravata | 3.456.875.888.640 | 0,152228 |
| Total | 22.708.579.049.472 | 1.000000 |
A tabela a seguir mostra os possíveis resultados se o banqueiro acertar um 3 em vez de um 9. O valor esperado da posição é 0,516019 - 0,371799 = 0,118419.
Acerto no Banqueiro 3 contra 9
| Mão vencedora | Combinações | Probabilidade |
|---|---|---|
| Banqueiro | 11.718.056.230.912 | 0,516019 |
| Jogador | 8.443.028.373.504 | 0,371799 |
| Gravata | 2.547.494.445.056 | 0,112182 |
| Total | 22.708.579.049.472 | 1.000000 |
Conforme demonstrado acima, o valor esperado de um banqueiro 3 contra 9 é de 0,118419 para empate e 0,043777 para manter a posição. As probabilidades favorecem fortemente a compra de carta, por uma margem de 7,46%.
Análise do Banqueiro 5 vs. 4
Embora eu já tenha argumentado que o valor esperado do jogo é maior na mão do banqueiro se ele tirar um 5 em vez de um 4, vamos analisar essa situação especificamente. As tabelas a seguir consideram apenas as mãos em que a mão do banqueiro tem um total de duas cartas igual a 5, a mão do jogador tirou um 4 e o jogador que age com a mão do jogador tira uma carta com um total de duas cartas igual a 5.
A tabela a seguir mostra os possíveis resultados se o banqueiro parar em um 5 em vez de um 4. O valor esperado de parar é 0,95 × 0,238182 - 0,608714 = -0,382441, assumindo uma comissão de 5% sobre as vitórias.
Posição no banqueiro 5 contra 4
| Mão vencedora | Combinações | Probabilidade |
|---|---|---|
| Banqueiro | 5.399.045.406.720 | 0,238182 |
| Jogador | 13.798.139.031.552 | 0,608714 |
| Gravata | 3.470.505.148.416 | 0,153104 |
| Total | 22.667.689.586.688 | 1.000000 |
A tabela a seguir mostra os possíveis resultados se o banqueiro acertar um 5 em vez de um 4. O valor esperado da posição é 0,95 × 0,262186 - 0,625426 = -0,376349, considerando uma comissão de 5% sobre os ganhos.
Acerto no Banqueiro 5 contra 4
| Mão vencedora | Combinações | Probabilidade |
|---|---|---|
| Banqueiro | 5.943.157.137.408 | 0,262186 |
| Jogador | 14.176.959.873.024 | 0,625426 |
| Gravata | 2.547.572.576.256 | 0,112388 |
| Total | 22.667.689.586.688 | 1.000000 |
Conforme mostrado acima, o valor esperado de um banqueiro 5 contra 4 é -0,376349 para empate e -0,382441 para manter a posição. As probabilidades favorecem ligeiramente a compra de carta, por uma margem de 0,61%.
Análise do Jogador 5
As duas tabelas a seguir mostram os possíveis resultados de uma mão do jogador com duas cartas, totalizando cinco, assumindo que a mão do banqueiro não tenha um par natural e que o banqueiro acertará tanto um 3 contra 9 quanto um 5 contra 4.
A tabela a seguir mostra os possíveis resultados se o jogador que age na Mão do Jogador parar com um total de cinco cartas. O valor esperado nessa situação é 0,444715 - 0,469428 = -0,024713, considerando uma comissão de 5% sobre os ganhos.
Posicione-se no Jogador 5
| Mão vencedora | Combinações | Probabilidade |
|---|---|---|
| Banqueiro | 31.757.731.375.104 | 0,469428 |
| Jogador | 30.085.834.328.064 | 0,444715 |
| Gravata | 5.808.447.387.648 | 0,085858 |
| Total | 67.652.013.090.816 | 1.000000 |
A tabela a seguir mostra os possíveis resultados se o jogador que age na Mão do Jogador comprar uma mão com um total de cinco cartas. O valor esperado nesse caso é 0,442311 - 0,429768 = 0,012543, considerando uma comissão de 5% sobre os ganhos.
Empate com o Jogador 5
| Mão vencedora | Combinações | Probabilidade |
|---|---|---|
| Banqueiro | 29.074.691.589.120 | 0,429768 |
| Jogador | 29.923.240.656.384 | 0,442311 |
| Gravata | 8.654.080.845.312 | 0,127921 |
| Total | 67.652.013.090.816 | 1.000000 |
Conforme mostrado acima, o total esperado de cinco na mão do jogador é de -0,024713 para quem permanece na mão e de 0,012543 para quem compra uma carta. As probabilidades favorecem o jogador que pede carta, por uma margem de 3,73%.
Apostando contra um jogador que está com cinco pontos
Peço desculpas se não me aprofundar tanto na análise da estratégia da Mão do Banqueiro caso o jogador que age com a Mão do Jogador cometa o erro de parar com um total de cinco cartas.
Com uma mão de banqueiro 3 contra 9, o valor esperado é 0,051725 maior ao ficar de pé.
Com uma mão de banqueiro 5 contra 4, o valor esperado é 0,005315 maior ao ficar de pé.
Dadas as limitadas situações de livre arbítrio, a estratégia da Mão do Jogador é conhecida como "dominada". Em outras palavras, independentemente de como a Mão do Banqueiro jogue a situação de dois livres arbítrio, a Mão do Jogador deve acertar com um total de cinco. Assumindo que a Mão do Jogador acertará com cinco, a Mão do Banqueiro deve acertar tanto 3 contra 9 quanto 5 contra 4. Supondo que ambos os lados façam isso, os valores esperados para ambos os lados do jogo são os seguintes. O valor esperado para o Banqueiro considera uma comissão de 5% sobre as vitórias.
- Jogador: -0,012351
- Banqueiro: -0,010579
Essa estratégia se resume às regras do bacará. Se esses números lhe parecerem familiares, é porque são os valores esperados para o bacará. Em outras palavras, se dois jogadores de lógica jogassem a variante de livre-arbítrio limitado do jogo de cartas "chemin de fer", o resultado seria uma estratégia semelhante à do bacará.
Devo observar que, se adicionarmos livre arbítrio a um 4 do Banqueiro contra um ás, então o jogador deve pedir carta nessa situação. Sob as regras de livre arbítrio limitado descritas por Scarne, o Banqueiro é forçado a parar nessa situação. Se o Banqueiro pudesse pedir carta com um 4 contra um ás, o restante da estratégia permaneceria o mesmo descrito acima. Os valores esperados mudariam, da seguinte forma:
- Jogador: -0,012359
- Banqueiro: -0,010575
Note que esses valores esperados são um pouco melhores para o Banqueiro e um pouco piores para o Jogador. Não sei por que o Banqueiro para no 4 contra o Ás (considerando uma jogada ruim para o Banqueiro). Talvez seja um erro na criação das regras do bacará.
Conclusão
Considerando que ambos os lados empatam em todas as situações em que o livre arbítrio é permitido, como deveria ser, seguem as probabilidades de cada resultado, assumindo oito baralhos.
- Vitória do jogador = 0,446247
- Vitória do banqueiro = 0,458597
- Empate = 0,095156
O valor esperado da mão do jogador é -0,012351. Considerando a comissão de 5% sobre as vitórias, a mão do banqueiro tem um valor esperado de -0,010579. Esses valores são os mesmos do bacará tradicional.
Análise das Regras de Fleming
A seguir, apresento minha análise do Chemin de Fer, de acordo com as regras de Casino Royale, de Ian Fleming. A obra "The Doctrine of Chances", de Stuart N. Ethier, corrobora essas regras, descrevendo como o jogo era praticado no início do século XX. Conforme explicado na seção de regras acima, Fleming afirmou que o jogo era jogado com seis baralhos e livre arbítrio em todas as situações, exceto quando um dos lados obtivesse um Natural.
Após muita análise, descobri que existem apenas seis situações em que a jogada correta depende de como o outro lado joga. Aqui estão elas:
- Total de 5 cartas do jogador: 5
- O banqueiro tem um total de 6 com duas cartas, após o jogador ficar parado.
- O banqueiro tem um total de 3 cartas após o jogador comprar um 9.
- O banqueiro tem um total de 4 com duas cartas, após o jogador sacar um ás.
- O banqueiro tem um total de 5 com duas cartas, após o jogador comprar um 4.
A estratégia do Banqueiro é jogar da mesma forma que o Jogador. Em outras palavras, se o Jogador tirar um cinco, o Banqueiro também deve tirar um cinco nas outras quatro situações listadas. Enquanto isso, o Jogador deve jogar de forma oposta à maneira como o Banqueiro costuma jogar nas quatro situações que dependem da estratégia.
A tabela a seguir mostra o valor esperado para ambas as mãos, de acordo com as duas estratégias possíveis para cada mão. A estratégia do Banqueiro refere-se à forma como o Banqueiro joga todas as quatro mãos listadas acima. O valor esperado da estratégia do Banqueiro pressupõe uma comissão de 5% sobre os ganhos.
Valores esperados de livre arbítrio pleno
| Jogador Estratégia | Banqueiro Estratégia | Jogador Valor de Exp | Banqueiro Valor de Exp |
|---|---|---|---|
| Ficar | Ficar | -0,015501 | 0.015501 |
| Ficar | Bater | -0,008734 | 0,008734 |
| Bater | Ficar | -0,011993 | 0,011993 |
| Bater | Bater | -0,013809 | 0,013809 |
Se dois lógicos jogassem chemin de fer, ambos aleatorizariam sua estratégia, assim como em pedra-papel-tesoura. Em particular, aqui estão as probabilidades para ambos os lados:
- Jogador: Acertou no cinco com probabilidade de 78,84%.
- Banqueiro: Acertar nas quatro situações listadas tem a mesma probabilidade de 78,84%.
Contanto que pelo menos um dos lados utilize a estratégia de aleatorização acima, os valores esperados para ambos os lados serão os seguintes, considerando novamente uma comissão de 0% para as vitórias do Banqueiro:
- Jogador: -0,012735
- Banqueiro: 0,012735
Gostaria de comentar que Ethier chega a uma conclusão diferente da minha. Isso parece ocorrer porque ele não considera que o Banqueiro pedir carta com seis, depois do Jogador parar, seja algo que ele possa fazer. Em vez disso, Ethier assume que o Banqueiro sempre para nessa situação.
Links externos
- Regras do Chemin de Fer estabelecidas pela Comissão de Jogos de Massachusetts. Observe que elas não conferem ao banqueiro qualquer livre arbítrio.
- Página da Wikipédia em Chemin de Fer .
- A Doutrina das Probabilidades: Aspectos Probabilísticos do Jogo, de Stewart N. Ethier. Este livro didático universitário dedica várias páginas à matemática do Chemin de Fer.

