Nesta página
Apêndice Sic Bo
Nesta página
Introdução

Imagem retirada do livro de regras do Claridge Hotel/Casino.
Bônus online Sic Bo Ver tudo
- Baixo :
Essa aposta não teria vantagem da casa se não fosse pela exceção da tripla. A probabilidade de uma tripla 1, 2 ou 3 é 3/216. A probabilidade de qualquer total entre 3 e 10 é 1/2, ou 108/216. Portanto, a probabilidade de uma tripla vencedora é 108/216 - 3/216 = 105/216. A vantagem do jogador é, portanto, (105/216)*(+1) + (111/216)*(-1) = -6/216 ≈ -2,78%.
- Alto : Veja Baixo.
- Número específico :
A probabilidade de rolar zero de um número específico é (5/6) 3 =125/216.
A probabilidade de rolar um de um número específico é 3*(1/6) 1 *(5/6) 2 = 75/216.
A probabilidade de rolar dois números específicos é 3*(1/6) 2 *(5/6) 1 = 15/216.
A probabilidade de rolar três números específicos é (1/6) 3 = 1/216.
A vantagem do jogador é, portanto, (125/216)*(-1) + (75/216)*(+1) + (15/216)*(+2) + (1/216)*(+3) = -17/216 =~-7,780%. - Total de 4 :
Existem 3 maneiras de rolar 4: (1+1+2, 1+2+1, 2+1+1). A vantagem do jogador é, portanto, 3/216*(+60) + (213/216)*(-1) = -33/216 = -15,278%.
- Total de 5 :
Existem 6 maneiras de rolar 5: (1+1+3, 1+3+1, 3+1+1, 1+2+2, 2+1+2, 2+2+1). A vantagem do jogador é, portanto, 6/216*(+30) + (210/216)*(-1) =-30/216 = -13,889%.
- Total de 6 :
Existem 10 maneiras de rolar 6: (1+1+4, 1+4+1, 4+1+1, 1+2+3, 1+3+2, 2+1+3, 2+3+1, 3+1+2, 3+2+1, 2+2+2). A vantagem do jogador é, portanto, 10/216*(+17) + (206/216)*(-1) = -36/216 = -16,667%.
- Total de 7 :
Existem 15 maneiras de rolar um 7: (1+1+5, 1+5+1, 5+1+1, 1+2+4, 1+4+2, 2+1+4, 2+4+1, 4+1+2, 4+2+1, 1+3+3, 3+1+3, 3+3+1, 2+2+3, 2+3+2, 3+2+2). A vantagem do jogador é, portanto, 15/216*(+12) + (201/216)*(-1) = -21/216 = -9,722%.
- Total de 8 :
Existem 21 maneiras de rolar 8: (1-6-6 * 3 maneiras, 1-2-5 * 6 maneiras, 1-3-4 * 6 maneiras, 2-2-4 * 3 maneiras, 2-3-3 * 3 maneiras). A vantagem do jogador é, portanto, 21/216*(+8) + (195/216)*(-1) = -27/216 = -12,500%.
- Total de 9 :
Existem 25 maneiras de rolar 9: (1-2-6 * 6 maneiras, 1-3-5 * 6 maneiras, 1-4-4 * 3 maneiras, 2-2-5 * 3 maneiras, 2-3-4 * 6 maneiras, 3-3-3 * 1 maneira). A vantagem do jogador é, portanto, 25/216*(+6) + (191/216)*(-1) = -41/216 = -18,982%.
- Total de 10 :
Existem 27 maneiras de rolar 10: (1-3-6 * 6 maneiras, 1-4-5 * 6 maneiras, 2-2-6 * 3 maneiras, 2-3-5 * 6 maneiras, 2-4-4 * 3 maneiras, 3-3-4 * 3 maneiras). A vantagem do jogador é, portanto, 27/216*(+6) + (189/216)*(-1) = -27/216 = -12,500%.
- Total de 11 : Veja o total de 10
- Total de 12 : Veja o total de 9
- Total de 13 : Veja o total de 8
- Total de 14 : Veja o total de 7
- Total de 15 : Veja o total de 6
- Total de 16 : Veja o total de 5
- Total de 17 : Veja o total de 4
- Dois números :
Vamos supor que os dois números escolhidos sejam 1 e 2. Existem 30 combinações com 1 e 2: 1-2-1 * 3 maneiras, 1-2-2 * 3 maneiras, 1-2-3 * 6 maneiras, 1-2-4 * 6 maneiras, 1-2-5 * 6 maneiras, 1-2-6 * 6 maneiras. A vantagem do jogador é, portanto, 30/216*(+5) +(186/216)*(-1) = -36/216 = -16,667%.
- Trinca específica :
Só existe uma maneira de rolar um trio específico. A vantagem do jogador é, portanto, 1/216*(+180) + (215/216)*(-1) = -35/216 = -16,20%.
- Qualquer trio :
Existem 6 maneiras de rolar uma trinca. A vantagem do jogador é, portanto, 6/216*(+30) +(210/216)*(-1) = -30/216 = -13,889%.
- Par específico :
Vamos supor que o par escolhido seja o número 1. Existem 16 maneiras de se obter dois ou três desses números: 1+1+1, 1+1+2 * 3 maneiras, 1+1+3 * 3 maneiras, 1+1+4 * 3 maneiras, 1+1+5 * 3 maneiras, 1+1+6 * 3 maneiras. A vantagem do jogador é, portanto, 16/216*(+10) + (200/216)*(-1) = -72/216 = -18,52%.
A seguir, apresentamos uma fórmula para s pontos em n dados, extraída de "The Theory of Gambling and Statistical Logic" de Richard A. Epstein, fórmula 5-14.
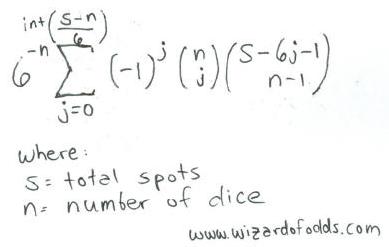
Por exemplo, vamos analisar o número de maneiras de obter 11 pontos em 3 dados.
int[(sn)/6] = int[(11-3)/6] = int[1.33] = 1
O total seria 6 -3 * [-1 0 *combin(3,0)*combin(11-6*0-1,3-1) + -1 1 *combin(3,1)*combin(11-6*1-1,3-1) ] =
1/216 * [1*1*combinar(10,2) + -1*3*combinar(4,2)] =
1/216 * [1*1*45 + -1*3*6] =
1/216 * [45-18] = 27/216 = 12,5%
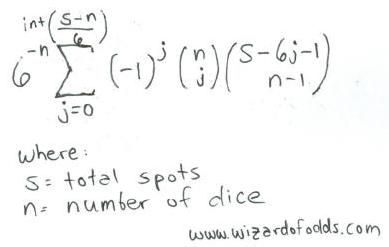













.png)










