Nesta página
Quadrados do Super Bowl
Introdução
O termo "Super Bowl Squares" geralmente se refere a apostas no último dígito da pontuação total de cada time no Super Bowl. Pode ser feito apenas no final do jogo ou quarto a quarto. Geralmente é jogado entre amigos, sem ninguém recolhendo o prêmio, onde todos têm chances iguais.
Para o Super Bowl 54, a casa de apostas Circa Sports Books em Las Vegas (localizada na esquina da D com a Golden Gate) ofereceu 400 apostas onde o jogador podia escolher seus próprios quadrados. Esta página analisa principalmente a probabilidade de todas as 400 apostas serem vencedoras e o valor de cada aposta.
Versão Aleatória
Imagino que a maioria das pessoas que encontrarem esta página esteja mais interessada em saber como realizar o que chamarei de versão aleatória do Super Bowl Squares. Geralmente, isso é feito entre amigos, onde ninguém fica com o prêmio. É uma maneira divertida de apostar no Super Bowl para quem não tem ideia de em que apostar e/ou não se importa com quem ganha. A seguir, descrevo como isso geralmente é feito.
- Será desenhada uma grade de 10x10, formando 100 quadrados, como em um tabuleiro de Batalha Naval.
- O preço será determinado por metro quadrado, por exemplo, 10 dólares.
- Devem ser estabelecidas regras sobre como o prêmio total será dividido, por exemplo, 20% para os trimestres 1, 2 e 3, e 40% para a pontuação final.
- Uma equipe deve ser escrita à esquerda ou à direita da grade e a outra equipe na parte superior ou inferior.
- Os compradores escolherão quadrados na grade, de acordo com a quantidade comprada, e escreverão seus nomes em cada um deles.
- Após todos os espaços terem sido comprados ou se for determinado que é improvável que haja mais compradores, quem estiver administrando o bolão receberá 10 cartas de baralho, de Ás a 9, e uma figura (valete, dama e rei). Cada carta terá o seguinte valor:
- A = um ponto.
- 2-9 = valor do pip.
- Carta com figura = 0 pontos.
- As cartas devem ser embaralhadas e, em seguida, de forma sistemática, uma carta deve ser atribuída a cada linha da grade. O resultado final deve ser que cada linha esteja numerada de 0 a 9 de forma aleatória.
- O mesmo processo deverá ser repetido para as colunas.
- O resultado final deverá ser semelhante ao exemplo a seguir.
- Após cada quarto e ao final da partida, o último dígito do placar de cada equipe deverá ser anotado. Consultando os cabeçalhos das linhas e colunas correspondentes a esse placar, será determinado o vencedor daquele quarto/partida.
- Caso o vencedor seja um quadrado vazio, regras devem ser estabelecidas previamente sobre o que fazer. Por exemplo, acumular o prêmio para o próximo trimestre/fim de jogo. Se o resultado final for um quadrado vazio, uma regra deve ser definida previamente sobre o que fazer, como distribuir o dinheiro entre os vencedores dos trimestres proporcionalmente ou distribuir as cartas para determinar o vencedor.
Segue abaixo um exemplo de jogo de tabuleiro "Super Bowl Squares".
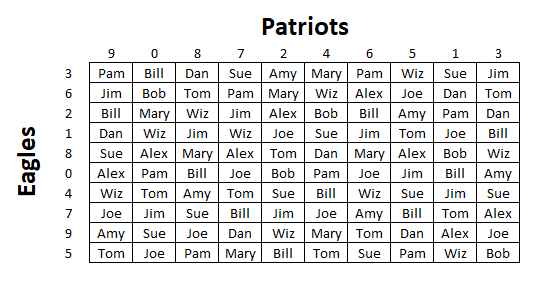
Vejamos um exemplo, baseado no Super Bowl de 2018. Aqui está a súmula do jogo.
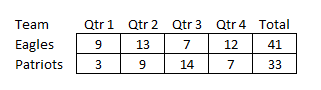
Ao final do primeiro quarto, o placar era Eagles 9 e Patriots 3. Seguindo pela linha 9 e descendo pela coluna 3, encontramos que Joe foi o vencedor do primeiro quarto.
Ao final do segundo quarto, o placar era Eagles 22 e Patriots 12. Os dígitos finais dos placares são Eagles 2 e Patriots 2. Na segunda linha e na segunda coluna, encontramos que Alex foi o vencedor do segundo quarto.
Ao final do terceiro quarto, o placar era Eagles 29 e Patriots 26. Os dígitos finais dos placares são Eagles 9 e Patriots 6. Seguindo pela linha 9 e descendo pela coluna 6, descobrimos que Tom foi o vencedor do terceiro quarto.
Ao final da partida, o placar era Eagles 41 e Patriots 33. Os dígitos finais dos placares são Eagles 1 e Patriots 3. Na primeira linha e na terceira coluna, encontramos que Bill foi o vencedor da partida.
Conforme o acordo de distribuição, Joe, Alex e Tom receberiam US$ 200 cada, e Bill, US$ 400.
Escolha o seu próprio quadrado
A casa de apostas Circa, localizada na esquina da D com a Golden Gate em Las Vegas, oferecia apostas em quadrados não aleatórios para o Super Bowl. Em outras palavras, o jogador podia escolher o dígito final de cada equipe. Essas apostas estavam disponíveis para os três primeiros quartos e para o jogo completo, totalizando 400 apostas.
Para analisá-los, examinei todos os jogos da NFL das temporadas de 2000 a 2014, totalizando 3.985 partidas. As quatro tabelas a seguir mostram a distribuição do dígito final de cada time em cada jogo. Contei cada jogo duas vezes, invertendo os placares, para obter uma amostra maior e garantir simetria.
Primeiro trimestre
| Equipe 1 | Equipe 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 1532 | 23 | 9 | 681 | 274 | 5 | 108 | 986 | 4 | 19 |
| 1 | 23 | 0 | 0 | 5 | 3 | 0 | 1 | 11 | 0 | 0 |
| 2 | 9 | 0 | 0 | 0 | 3 | 0 | 0 | 8 | 1 | 0 |
| 3 | 681 | 5 | 0 | 260 | 66 | 0 | 28 | 393 | 0 | 7 |
| 4 | 274 | 3 | 3 | 66 | 20 | 0 | 2 | 109 | 0 | 0 |
| 5 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 0 |
| 6 | 108 | 1 | 0 | 28 | 2 | 0 | 0 | 44 | 0 | 0 |
| 7 | 986 | 11 | 8 | 393 | 109 | 4 | 44 | 568 | 0 | 1 |
| 8 | 4 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 19 | 0 | 0 | 7 | 0 | 0 | 0 | 1 | 0 | 0 |
Segundo trimestre
| Equipe 1 | Equipe 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 566 | 105 | 22 | 400 | 289 | 18 | 183 | 486 | 33 | 44 |
| 1 | 105 | 20 | 6 | 78 | 51 | 2 | 31 | 107 | 1 | 7 |
| 2 | 22 | 6 | 2 | 4 | 16 | 1 | 4 | 20 | 0 | 1 |
| 3 | 400 | 78 | 4 | 254 | 179 | 13 | 115 | 343 | 14 | 31 |
| 4 | 289 | 51 | 16 | 179 | 144 | 9 | 82 | 247 | 12 | 22 |
| 5 | 18 | 2 | 1 | 13 | 9 | 0 | 2 | 19 | 2 | 1 |
| 6 | 183 | 31 | 4 | 115 | 82 | 2 | 38 | 126 | 8 | 18 |
| 7 | 486 | 107 | 20 | 343 | 247 | 19 | 126 | 486 | 29 | 47 |
| 8 | 33 | 1 | 0 | 14 | 12 | 2 | 8 | 29 | 0 | 0 |
| 9 | 44 | 7 | 1 | 31 | 22 | 1 | 18 | 47 | 0 | 4 |
Terceiro trimestre
| Equipe 1 | Equipe 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 342 | 116 | 49 | 294 | 222 | 25 | 141 | 380 | 61 | 46 |
| 1 | 116 | 72 | 9 | 84 | 105 | 14 | 44 | 152 | 24 | 21 |
| 2 | 49 | 9 | 2 | 19 | 28 | 3 | 7 | 41 | 5 | 7 |
| 3 | 294 | 84 | 19 | 252 | 185 | 18 | 114 | 249 | 52 | 42 |
| 4 | 222 | 105 | 28 | 185 | 200 | 22 | 90 | 271 | 37 | 32 |
| 5 | 25 | 14 | 3 | 18 | 22 | 6 | 3 | 31 | 2 | 2 |
| 6 | 141 | 44 | 7 | 114 | 90 | 3 | 52 | 125 | 21 | 15 |
| 7 | 380 | 152 | 41 | 249 | 271 | 31 | 125 | 342 | 72 | 51 |
| 8 | 61 | 24 | 5 | 52 | 37 | 2 | 21 | 72 | 14 | 9 |
| 9 | 46 | 21 | 7 | 42 | 32 | 2 | 15 | 51 | 9 | 8 |
Fim do jogo
| Equipe 1 | Equipe 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 158 | 104 | 56 | 279 | 177 | 46 | 112 | 280 | 82 | 46 |
| 1 | 104 | 42 | 20 | 93 | 189 | 33 | 52 | 139 | 90 | 45 |
| 2 | 56 | 20 | 4 | 31 | 38 | 19 | 19 | 44 | 13 | 26 |
| 3 | 279 | 93 | 31 | 110 | 121 | 31 | 127 | 184 | 59 | 64 |
| 4 | 177 | 189 | 38 | 121 | 134 | 46 | 73 | 285 | 72 | 50 |
| 5 | 46 | 33 | 19 | 31 | 46 | 8 | 19 | 65 | 42 | 15 |
| 6 | 112 | 52 | 19 | 127 | 73 | 19 | 46 | 98 | 37 | 43 |
| 7 | 280 | 139 | 44 | 184 | 285 | 65 | 98 | 170 | 70 | 73 |
| 8 | 82 | 90 | 13 | 59 | 72 | 42 | 37 | 70 | 30 | 20 |
| 9 | 46 | 45 | 26 | 64 | 50 | 15 | 43 | 73 | 20 | 14 |
As quatro tabelas a seguir mostram a probabilidade de cada quadrado ser vencedor, com base nos dados acima.
Primeiro trimestre
| Equipe 1 | Equipe 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 0,192221 | 0,002886 | 0,001129 | 0,085445 | 0,034379 | 0,000627 | 0,013551 | 0,123714 | 0,000502 | 0,002384 |
| 1 | 0,002886 | 0,000000 | 0,000000 | 0,000627 | 0,000376 | 0,000000 | 0,000125 | 0,001380 | 0,000000 | 0,000000 |
| 2 | 0,001129 | 0,000000 | 0,000000 | 0,000000 | 0,000376 | 0,000000 | 0,000000 | 0,001004 | 0,000125 | 0,000000 |
| 3 | 0,085445 | 0,000627 | 0,000000 | 0,032622 | 0,008281 | 0,000000 | 0,003513 | 0,049310 | 0,000000 | 0,000878 |
| 4 | 0,034379 | 0,000376 | 0,000376 | 0,008281 | 0,002509 | 0,000000 | 0,000251 | 0,013676 | 0,000000 | 0,000000 |
| 5 | 0,000627 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000502 | 0,000000 | 0,000000 |
| 6 | 0,013551 | 0,000125 | 0,000000 | 0,003513 | 0,000251 | 0,000000 | 0,000000 | 0,005521 | 0,000000 | 0,000000 |
| 7 | 0,123714 | 0,001380 | 0,001004 | 0,049310 | 0,013676 | 0,000502 | 0,005521 | 0,071267 | 0,000000 | 0,000125 |
| 8 | 0,000502 | 0,000000 | 0,000125 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 |
| 9 | 0,002384 | 0,000000 | 0,000000 | 0,000878 | 0,000000 | 0,000000 | 0,000000 | 0,000125 | 0,000000 | 0,000000 |
Segundo trimestre
| Equipe 1 | Equipe 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 0,071016 | 0,013174 | 0,002760 | 0,050188 | 0,036261 | 0,002258 | 0,022961 | 0,060979 | 0,004141 | 0,005521 |
| 1 | 0,013174 | 0,002509 | 0,000753 | 0,009787 | 0,006399 | 0,000251 | 0,003890 | 0,013425 | 0,000125 | 0,000878 |
| 2 | 0,002760 | 0,000753 | 0,000251 | 0,000502 | 0,002008 | 0,000125 | 0,000502 | 0,002509 | 0,000000 | 0,000125 |
| 3 | 0,050188 | 0,009787 | 0,000502 | 0,031870 | 0,022459 | 0,001631 | 0,014429 | 0,043036 | 0,001757 | 0,003890 |
| 4 | 0,036261 | 0,006399 | 0,002008 | 0,022459 | 0,018068 | 0,001129 | 0,010289 | 0,030991 | 0,001506 | 0,002760 |
| 5 | 0,002258 | 0,000251 | 0,000125 | 0,001631 | 0,001129 | 0,000000 | 0,000251 | 0,002384 | 0,000251 | 0,000125 |
| 6 | 0,022961 | 0,003890 | 0,000502 | 0,014429 | 0,010289 | 0,000251 | 0,004768 | 0,015809 | 0,001004 | 0,002258 |
| 7 | 0,060979 | 0,013425 | 0,002509 | 0,043036 | 0,030991 | 0,002384 | 0,015809 | 0,060979 | 0,003639 | 0,005897 |
| 8 | 0,004141 | 0,000125 | 0,000000 | 0,001757 | 0,001506 | 0,000251 | 0,001004 | 0,003639 | 0,000000 | 0,000000 |
| 9 | 0,005521 | 0,000878 | 0,000125 | 0,003890 | 0,002760 | 0,000125 | 0,002258 | 0,005897 | 0,000000 | 0,000502 |
Terceiro trimestre
| Equipe 1 | Equipe 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 0,042911 | 0,014555 | 0,006148 | 0,036888 | 0,027854 | 0,003137 | 0,017691 | 0,047679 | 0,007654 | 0,005772 |
| 1 | 0,014555 | 0,009034 | 0,001129 | 0,010540 | 0,013174 | 0,001757 | 0,005521 | 0,019072 | 0,003011 | 0,002635 |
| 2 | 0,006148 | 0,001129 | 0,000251 | 0,002384 | 0,003513 | 0,000376 | 0,000878 | 0,005144 | 0,000627 | 0,000878 |
| 3 | 0,036888 | 0,010540 | 0,002384 | 0,031619 | 0,023212 | 0,002258 | 0,014304 | 0,031242 | 0,006524 | 0,005270 |
| 4 | 0,027854 | 0,013174 | 0,003513 | 0,023212 | 0,025094 | 0,002760 | 0,011292 | 0,034003 | 0,004642 | 0,004015 |
| 5 | 0,003137 | 0,001757 | 0,000376 | 0,002258 | 0,002760 | 0,000753 | 0,000376 | 0,003890 | 0,000251 | 0,000251 |
| 6 | 0,017691 | 0,005521 | 0,000878 | 0,014304 | 0,011292 | 0,000376 | 0,006524 | 0,015684 | 0,002635 | 0,001882 |
| 7 | 0,047679 | 0,019072 | 0,005144 | 0,031242 | 0,034003 | 0,003890 | 0,015684 | 0,042911 | 0,009034 | 0,006399 |
| 8 | 0,007654 | 0,003011 | 0,000627 | 0,006524 | 0,004642 | 0,000251 | 0,002635 | 0,009034 | 0,001757 | 0,001129 |
| 9 | 0,005772 | 0,002635 | 0,000878 | 0,005270 | 0,004015 | 0,000251 | 0,001882 | 0,006399 | 0,001129 | 0,001004 |
Fim do jogo
| Equipe 1 | Equipe 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 0,019824 | 0,013049 | 0,007026 | 0,035006 | 0,022208 | 0,005772 | 0,014053 | 0,035132 | 0,010289 | 0,005772 |
| 1 | 0,013049 | 0,005270 | 0,002509 | 0,011669 | 0,023714 | 0,004141 | 0,006524 | 0,017440 | 0,011292 | 0,005646 |
| 2 | 0,007026 | 0,002509 | 0,000502 | 0,003890 | 0,004768 | 0,002384 | 0,002384 | 0,005521 | 0,001631 | 0,003262 |
| 3 | 0,035006 | 0,011669 | 0,003890 | 0,013802 | 0,015182 | 0,003890 | 0,015935 | 0,023087 | 0,007403 | 0,008030 |
| 4 | 0,022208 | 0,023714 | 0,004768 | 0,015182 | 0,016813 | 0,005772 | 0,009159 | 0,035759 | 0,009034 | 0,006274 |
| 5 | 0,005772 | 0,004141 | 0,002384 | 0,003890 | 0,005772 | 0,001004 | 0,002384 | 0,008156 | 0,005270 | 0,001882 |
| 6 | 0,014053 | 0,006524 | 0,002384 | 0,015935 | 0,009159 | 0,002384 | 0,005772 | 0,012296 | 0,004642 | 0,005395 |
| 7 | 0,035132 | 0,017440 | 0,005521 | 0,023087 | 0,035759 | 0,008156 | 0,012296 | 0,021330 | 0,008783 | 0,009159 |
| 8 | 0,010289 | 0,011292 | 0,001631 | 0,007403 | 0,009034 | 0,005270 | 0,004642 | 0,008783 | 0,003764 | 0,002509 |
| 9 | 0,005772 | 0,005646 | 0,003262 | 0,008030 | 0,006274 | 0,001882 | 0,005395 | 0,009159 | 0,002509 | 0,001757 |
As tabelas acima mostram que a contagem de alguns quadrados é zero, especialmente no primeiro trimestre. No entanto, a probabilidade de um jogo futuro cair nesse quadrado é claramente maior que zero. Para estimar a probabilidade nessas situações, analisei apenas o dígito final de cada equipe em cada jogo por trimestre, sem considerar sua correlação com o dígito da equipe adversária. A tabela a seguir mostra o resumo.
Dígitos terminais individuais — Contagem
| Dígito | 1º trimestre | 2º trimestre | 3º trimestre | Jogo |
|---|---|---|---|---|
| 0 | 3.641 | 2.146 | 1.676 | 1.340 |
| 1 | 43 | 408 | 641 | 807 |
| 2 | 21 | 76 | 170 | 270 |
| 3 | 1.440 | 1.431 | 1.309 | 1.099 |
| 4 | 477 | 1.051 | 1.192 | 1.185 |
| 5 | 9 | 67 | 126 | 324 |
| 6 | 183 | 607 | 612 | 626 |
| 7 | 2.124 | 1.910 | 1.714 | 1.408 |
| 8 | 5 | 99 | 297 | 515 |
| 9 | 27 | 175 | 233 | 396 |
| Total | 7.970 | 7.970 | 7.970 | 7.970 |
A seguir, apresentamos as mesmas informações em formato de probabilidade.
Dígitos terminais individuais — Probabilidade
| Dígito | 1º trimestre | 2º trimestre | 3º trimestre | Jogo |
|---|---|---|---|---|
| 0 | 0,456838 | 0,269260 | 0,210289 | 0,168130 |
| 1 | 0,005395 | 0,051192 | 0,080427 | 0,101255 |
| 2 | 0,002635 | 0,009536 | 0,021330 | 0,033877 |
| 3 | 0,180678 | 0,179548 | 0,164241 | 0,137892 |
| 4 | 0,059849 | 0,131870 | 0,149561 | 0,148683 |
| 5 | 0,001129 | 0,008407 | 0,015809 | 0,040652 |
| 6 | 0,022961 | 0,076161 | 0,076788 | 0,078545 |
| 7 | 0,266499 | 0,239649 | 0,215056 | 0,176662 |
| 8 | 0,000627 | 0,012422 | 0,037265 | 0,064617 |
| 9 | 0,003388 | 0,021957 | 0,029235 | 0,049686 |
Um exemplo de onde isso pode ser útil é na análise da aposta Circa nos dígitos finais 5 para os Chiefs e 1 para os 49ers no primeiro quarto, pagando 10.000 para 1 (ou +1.000.000 no formato de odds americanas). Tal combinação nunca ocorreu nas 15 temporadas usadas para esta página. No entanto, podemos ver que, ao final do primeiro quarto, a probabilidade de o dígito final ser 5 para qualquer equipe é de 0,001129 e, para um dígito final 1, é de 0,005395. Poderíamos estimar a probabilidade dessa aposta ser vencedora como 0,001129 × 0,005395 = 0,00000609, ou 1 em 164.137. Isso faz com que minha estimativa do retorno dessa aposta seja de 10.001/164.137 = 6,09%. Em outras palavras, uma vantagem da casa de 93,91%.
As tabelas a seguir mostram o retorno de todas as 400 apostas disponíveis. O cálculo é baseado na contagem direta de todas as combinações 10 por 10 dos dígitos terminais nos dados disponíveis, quando essa contagem é maior que 0. Quando é 0, utilizei as probabilidades de equipe única.
Tabela de Retorno do Primeiro Trimestre
| Equipe 1 | Equipe 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 99,95% | 43,58% | 33,99% | 81,17% | 61,88% | 47,11% | 55,56% | 74,23% | 25,14% | 71,76% |
| 1 | 43,58% | 5,82% | 7,11% | 15,75% | 18,86% | 6,09% | 9,42% | 20,84% | 1,69% | 9,14% |
| 2 | 33,99% | 7,11% | 3,47% | 14,28% | 11,33% | 2,98% | 6,05% | 25,19% | 94,12% | 4,46% |
| 3 | 81,17% | 15,75% | 14,28% | 61,98% | 19,05% | 20,40% | 26,70% | 54,24% | 8,50% | 65,96% |
| 4 | 61,88% | 18,86% | 11,33% | 19,05% | 12,80% | 13,52% | 3,79% | 28,72% | 3,75% | 15,21% |
| 5 | 47,11% | 6,09% | 2,98% | 20,40% | 13,52% | 1,28% | 7,78% | 37,69% | 0,71% | 3,83% |
| 6 | 55,56% | 9,42% | 6,05% | 26,70% | 3,79% | 7,78% | 13,18% | 28,16% | 4,32% | 7,78% |
| 7 | 74,23% | 20,84% | 25,19% | 54,24% | 28,72% | 37,69% | 28,16% | 53,45% | 8,36% | 3,78% |
| 8 | 25,14% | 1,69% | 94,12% | 8,50% | 3,75% | 0,71% | 4,32% | 8,36% | 0,20% | 1,06% |
| 9 | 71,76% | 9,14% | 4,46% | 65,96% | 15,21% | 3,83% | 0,78% | 3,78% | 1,06% | 5,74% |
Tabela de retorno do segundo trimestre
| Equipe 1 | Equipe 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 92,32% | 47,43% | 41,68% | 80,30% | 61,64% | 39,75% | 71,18% | 79,27% | 31,47% | 41,96% |
| 1 | 47,43% | 25,35% | 37,72% | 49,91% | 39,03% | 12,57% | 29,56% | 36,25% | 2,52% | 17,65% |
| 2 | 41,68% | 37,72% | 75,31% | 10,09% | 50,39% | 12,56% | 25,14% | 50,44% | 5,92% | 18,83% |
| 3 | 80,30% | 49,91% | 10,09% | 82,86% | 58,39% | 32,79% | 73,59% | 73,16% | 17,74% | 58,73% |
| 4 | 61,64% | 39,03% | 50,39% | 58,39% | 46,98% | 22,70% | 62,76% | 58,88% | 18,97% | 48,58% |
| 5 | 39,75% | 12,57% | 12,56% | 32,79% | 22,70% | 7,07% | 7,55% | 41,96% | 18,85% | 12,56% |
| 6 | 71,18% | 29,56% | 25,14% | 73,59% | 62,76% | 7,55% | 60,08% | 64,82% | 15,16% | 67,98% |
| 7 | 79,27% | 36,25% | 50,44% | 73,16% | 58,88% | 41,96% | 64,82% | 97,57% | 27,65% | 59,56% |
| 8 | 31,47% | 2,52% | 5,92% | 17,74% | 18,97% | 18,85% | 15,16% | 27,65% | 4,63% | 13,64% |
| 9 | 41,96% | 17,65% | 18,83% | 58,73% | 48,58% | 12,56% | 67,98% | 59,56% | 13,64% | 50,24% |
Tabela de retorno do terceiro trimestre
| Equipe 1 | Equipe 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 68,66% | 45,12% | 92,84% | 77,47% | 52,92% | 19,13% | 54,84% | 76,29% | 31,38% | 43,86% |
| 1 | 45,12% | 55,11% | 33,99% | 53,75% | 67,19% | 26,52% | 55,76% | 78,19% | 30,41% | 52,96% |
| 2 | 92,84% | 33,99% | 25,12% | 41,96% | 61,83% | 18,86% | 22,05% | 77,68% | 18,88% | 44,00% |
| 3 | 77,47% | 53,75% | 41,96% | 113,83% | 71,96% | 28,46% | 144,47% | 65,61% | 39,80% | 79,57% |
| 4 | 52,92% | 67,19% | 61,83% | 71,96% | 77,79% | 27,88% | 91,47% | 71,41% | 28,32% | 60,63% |
| 5 | 19,13% | 26,52% | 18,86% | 28,46% | 27,88% | 18,90% | 7,57% | 23,73% | 5,04% | 7,55% |
| 6 | 54,84% | 55,76% | 22,05% | 144,47% | 91,47% | 7,57% | 114,83% | 64,30% | 39,79% | 47,24% |
| 7 | 76,29% | 78,19% | 77,68% | 65,61% | 71,41% | 23,73% | 64,30% | 81,53% | 46,07% | 64,63% |
| 8 | 31,38% | 30,41% | 18,88% | 39,80% | 28,32% | 5,04% | 39,79% | 46,07% | 26,52% | 31,17% |
| 9 | 43,86% | 52,96% | 44,00% | 79,57% | 60,63% | 7,55% | 47,24% | 64,63% | 31,17% | 30,21% |
Tabela de Retorno ao Final do Jogo
| Equipe 1 | Equipe 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 101,10% | 66,55% | 70,97% | 91,02% | 79,95% | 58,29% | 85,72% | 73,78% | 62,76% | 58,29% |
| 1 | 66,55% | 26,88% | 31,62% | 71,18% | 45,06% | 31,47% | 65,90% | 88,95% | 29,36% | 71,14% |
| 2 | 70,97% | 31,62% | 15,11% | 49,01% | 48,16% | 14,54% | 36,00% | 69,56% | 20,55% | 32,95% |
| 3 | 91,02% | 71,18% | 49,01% | 91,09% | 92,61% | 29,56% | 81,27% | 117,74% | 56,26% | 101,18% |
| 4 | 79,95% | 45,06% | 48,16% | 92,61% | 68,93% | 43,86% | 69,61% | 67,94% | 46,07% | 79,05% |
| 5 | 58,29% | 31,47% | 14,54% | 29,56% | 43,86% | 10,14% | 30,04% | 61,98% | 18,97% | 28,42% |
| 6 | 85,72% | 65,90% | 36,00% | 81,27% | 69,61% | 30,04% | 101,58% | 93,45% | 35,28% | 41,00% |
| 7 | 73,78% | 88,95% | 69,56% | 117,74% | 67,94% | 61,98% | 93,45% | 87,45% | 44,79% | 69,61% |
| 8 | 62,76% | 29,36% | 20,55% | 56,26% | 46,07% | 18,97% | 35,28% | 44,79% | 19,20% | 31,62% |
| 9 | 58,29% | 71,14% | 32,95% | 101,18% | 79,05% | 28,42% | 41,00% | 69,61% | 31,62% | 52,87% |
Isenção de responsabilidade
Esta página se baseia apenas nas médias da NFL. Não existe um "jogo médio". Por exemplo, a previsão de pontos (over/under) para o Super Bowl de 2020 é de 54, muito acima da média da NFL. Se este jogo tiver uma pontuação tão alta, é provável que outros totais de pontos nos quartos, e consequentemente os totais finais, também sejam atingidos.
Vale ressaltar também que, de modo geral, a NFL tem apresentado uma pontuação mais alta desde o final do período analisado em 2014, provavelmente devido a novas regras que restringem defesas agressivas e possivelmente perigosas.
Gostaria de acrescentar que, se você fizesse cada aposta proporcionalmente ao que ela pagaria em caso de vitória, tornando-se assim indiferente ao resultado, já que cada bilhete premiado teria o mesmo valor, o retorno total seria de 60%, ou seja, uma vantagem da casa de 40%.
Dito isto, por favor, considere os resultados aqui apresentados com cautela.


